独立驱动电动汽车模型参考自适应稳定性控制

李家林，奥 迪，王 杨，熊 锐

（1. 广东工业大学 机电工程学院，广州 510006，中国；2. 澳门大学 科技学院，澳门 999078，中国；3. 吉林大学汽车仿真与控制国家重点实验室，长春 130012，中国）

四轮独立驱动电动汽车 (electric vehicles, EV)[1]不仅节能环保，而且可以通过轮毂电机将驱动力矩和制动力矩直接快速地传递给4个车轮，准确地识别出车轮的速度、扭矩、车轮侧角等优势，有助于提高车辆行驶过程中的侧向稳定性[2-7]和驾驶安全性。

据统计[8]，在2019年中国交通事故死亡人数中，机动车交通事故死亡人数约5.7万人，其中汽车交通事故死亡人数约4.3万人。因此，为减少由于车辆失控而导致交通事故的数量和严重性，对驾驶控制技术研究现状[9]进行深入分析总结，很多研究学者提出了各种不同的控制器[10-12]来提高汽车稳定性。

文献[13]提出了一种不完全依赖被控对象模型准确性的方法，将模糊控制应用于非线性系统。但该方法过于依赖专家经验，实用性有待进一步拓展。文献[14]提出了一种模型预测的控制方法，其动态性能好，对于模型的精度要求低，但由于系统模型实时迭代计算复杂，难以保证控制器的实时性。文献[15]提出了一种在对抗外部干扰有明显作用的非奇异快速终端滑模控制方法，但在控制过程中，由于驱动力矩高频抖振，进而引发系统高频抖振现象，从而导致驱动电机的疲劳磨损[16]，降低控制器性能。但以上文献中并未考虑系统参数的不确定性的影响，因此本文通过自适应控制来降低系统参数的不确定性。

针对汽车稳定性控制领域，文献[17]考虑到车辆主动前轮转向和纵向滑移率，通过设计自适应率来控制制动力分配给各个车轮，以达到车辆稳定状态。文献[18]利用模型参考算法中的自适应律来估计车辆前后轮侧偏刚度的变化，以确保控制器的鲁棒性，提高车辆横向动力学的自适应控制。

文献[19]提出了一种新型的自适应随机映射神经网络控制算法，使用该算法应用于主动前轮转向，能够快速适应参数时变的被控系统。在实际应用中，百度Apollo无人驾驶[20]项目运用模型参考自适应 (model reference adaptive control, MRAC) 控制算法在路径追踪和自适应不同的转向系统方面也取得了不错的效果，但以上自适应控制器并未在汽车直接横摆力矩控制中应用。此外，由上述自适应控制器所输出的横摆力矩无法直接分配至4个车轮，因此基于不同目标的力矩分配也是亟待解决的问题。

文献[21]中，采取前后车轮比例制动的控制策略，将所得横摆力矩按比例分配至各个车轮，虽有一定的控制效果，但其未考虑轮胎利用率等问题。在文献[22]中，利用基于零空间的控制重新分配方法，并考虑每个车轮的轮胎利用率的约束，但由于计算量较大，对控制器要求高，现有条件难以满足。

为了提高车辆行驶安全性，本文提出了一种基于MRAC的直接横摆力矩控制的方法。在上层控制器中，利用二自由度车辆模型和一组假定的参数来设计稳定性控制器，并利用Lyapunov函数稳定性分析得到自适应估计率来解决由于车辆在行驶过程中重要参数不恒定的问题。在下层力矩分配控制器中，考虑车辆轮胎利用率和电机输出限制，利用二次规划法进行优化分配，其不仅运算速度快，而且能处理多约束条件问题，以保证动态响应的实时性。最后，本文在双移线高低附着因数工况下利用CarSim与Simulink联合仿真。

1 车辆模型

1.1 汽车动力学模型

本文采用简化的线性单轨车辆模型作为车辆理想模型，并以此设计横摆力矩控制器。其二自由度线性车辆模型如图1所示。

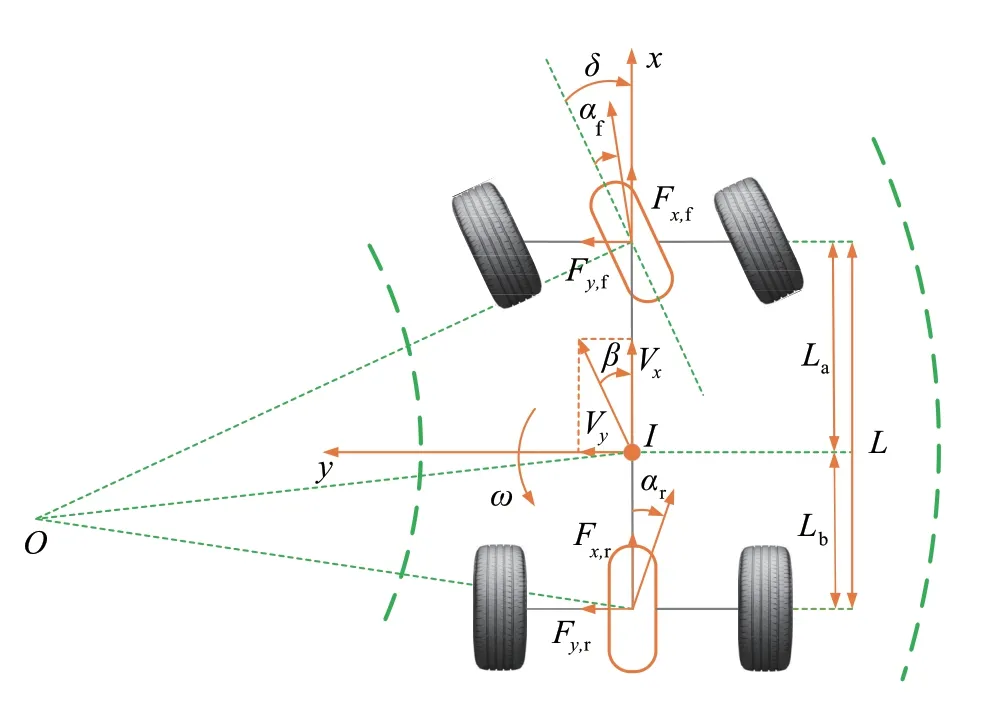
图1 二自由度线性车辆模型

在图1中，Kf、Kr分别为前后轮侧偏刚度；β、ω分别为质心侧偏角和横摆角速度；m为车身总质量；La、Lb分别为前后轴长度；L为轴长；Vx、Vy分别为纵向、侧向速度；δ为前轮转向角；αf、αr分别为前后轮侧偏角；I为车辆质心。

在该模型中做出了如下几个假设：

1） 前轮转向角很小；

2） 忽略所存在的各类阻力以及悬架系统动力学影响（空气、滚动以及摩擦）；

3） 轮胎性能和轮胎力在线性区域内。

二自由度线性车辆模型的运动微分方程如下：

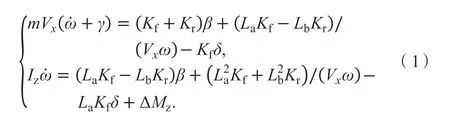
式中：Iz为绕Z轴的转动惯量；ΔMz附加横摆力矩。

化简得到状态空间方程式为：

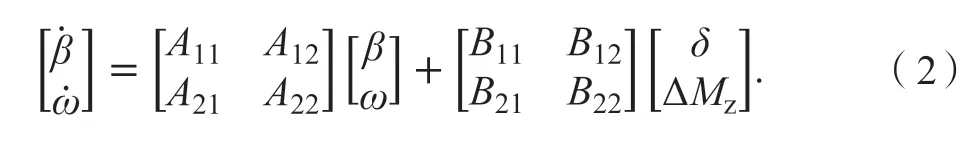
式中：

在车辆以恒定速度稳定向前以及过弯时，二自由度车辆模型ω与β的理想值可表示为：

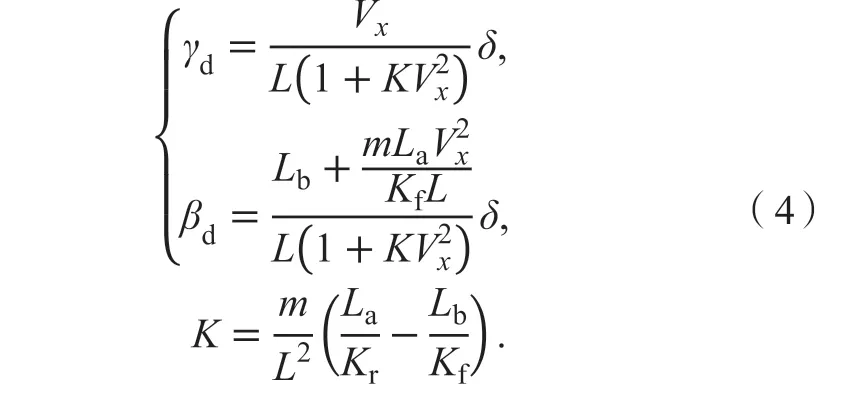
考虑道路附着情况，上述理想值需加以限定并进行修正，通过修正后的表达式为：

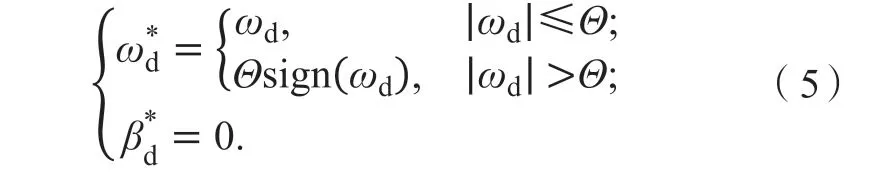
1.2 车轮模型

本文选用魔术轮胎公式(magic formula)[23-24]轮胎模型进行轮胎建模。该轮胎模型在文献中被广泛采用，并已被证明足够准确，可以预测实际的轮胎动力学。魔术轮胎公式[25]数学表达式如下：

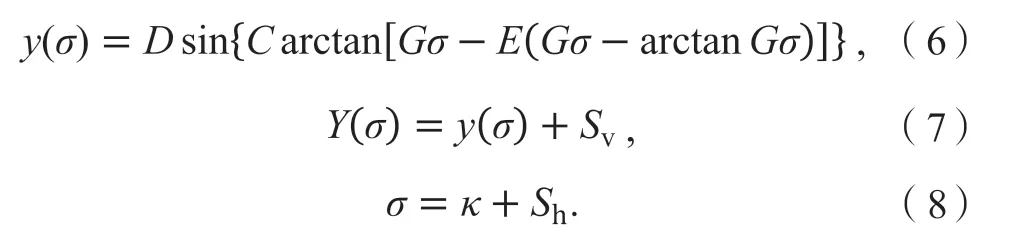
式中：κ为输入变量（车轮滑移率λ或轮胎侧滑角α/rad）；Y(κ)为输出变量轮胎纵向力Fxij/N或侧向力Fyij/N；Sh、Sv分别为曲线的水平和垂直方向漂移；G、C、D、E分别为刚度因子、形状因子、颠因子和曲率因子。

分析拟合实验数据得到：魔术轮胎纵向力Fxij、侧向力Fyij和轮胎垂向力Fzij。横、纵向力零点处的刚度因子为H，H=GCD，分别在纵向力和侧向力因子后加下标x、y表示。

Fxij、Fyij表达式中的因子分别为：

4个车轮的垂向力可表示为：

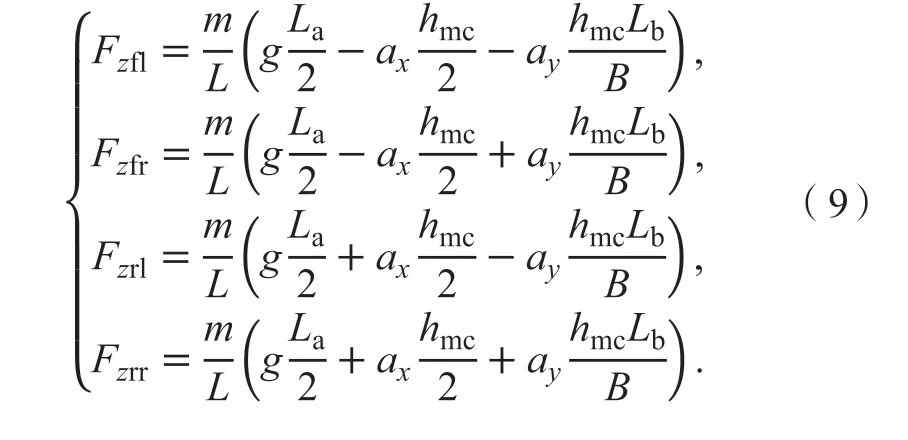
式中：Fzij为各轮垂向力；i= f,r;j= l,r;ax、ay为横向和纵向加速度；hmc为质心高度。

2 上层控制器

针对系统参数不确定的情况，本文在上层控制器中推导出一个使得跟踪误差渐近收敛，并且与系统参数无关的控制率。一般情况下，自适应参数估计不会完全收敛到与系统参数的真实值相等，但在过程中通过实时更新可无限接近其真实值，同时为保证控制率收敛，自适应控制器的控制输入、状态量和参数估计在运行过程中需保持有界。因此，为更好的估计未知系统参数、提高车辆行驶稳定性以及行驶舒适性[26]，提出了一种模型参考自适应直接横摆力矩控制器。系统控制构架具体设计如图2所示。

图2 系统控制架构图

2.1 MRAC推导

根据二自由度车辆运动模型，由式（2）可简化系统状态空间方程为：

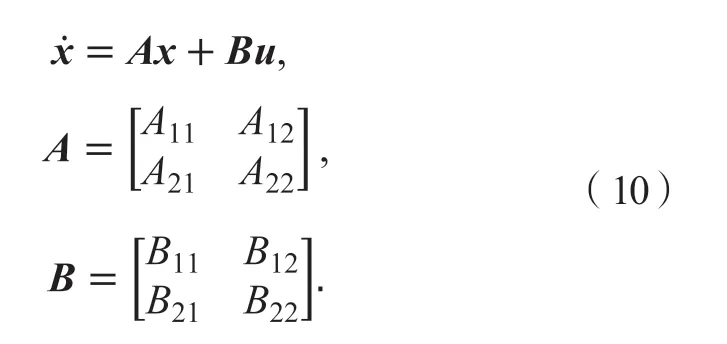
系统实际状态量为x与理想状态变量xd，设跟踪误差e及其导数为：

联立式（10）、（11）得动态误差方程：

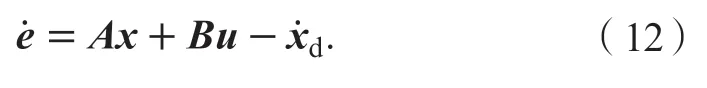
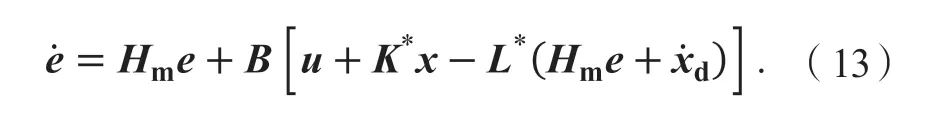
由式（13）可得系统控制率为：

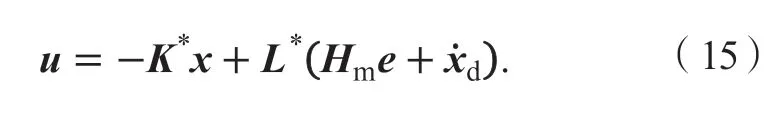
联立式（13）、（15）得动态误差为：

在控制率（15）中，K*、L*不能直接计算，因此对系统控制率未知参数进行估计得参数估计误差为：

根据未知系统参数估计值，设计自适应控制率为：

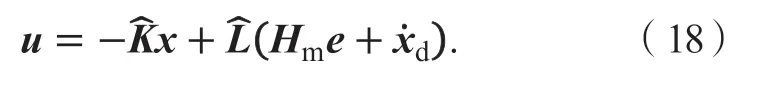
由式（12）、（13）、（17）、（18）得动态误差方程可改为：

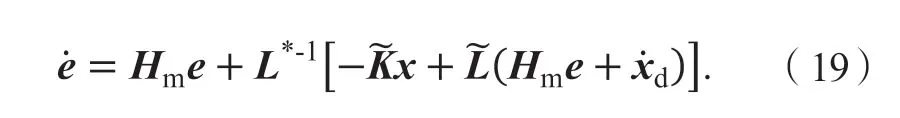
当矩阵L*正定，ρ= 1，当矩阵L*负定，ρ= 1，因此，定义矩阵Ω如下，且始终为正定矩阵。

2.2 MRAC稳定性证明

本文采用Lyapunov直接法来证明所提出控制器的稳定性，在MRAC控制器证明中，为建立更好的参数调节机制，保证系统能够收敛稳定，匹配到一个更为合理的Lyapunov函数至关重要。故定义Lyapunov方程为：

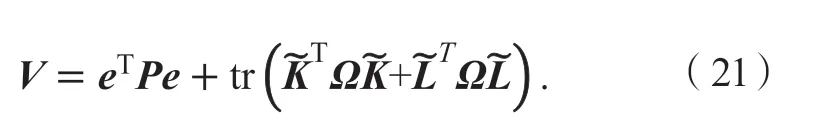
式中：P、Ω为正定对称矩阵，则V＞0；tr为矩阵的迹。

由Hurwitz矩阵性质可得：

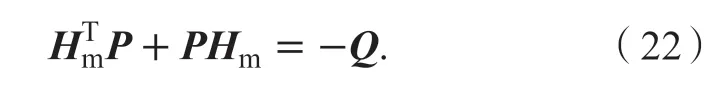
式中：Q任意正定对称矩阵。

对Lyapunov矩阵进行求导得

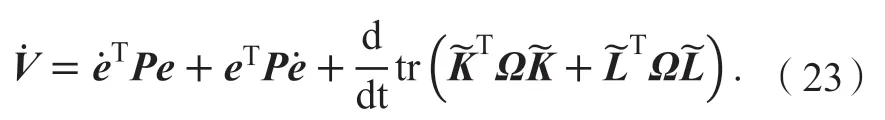
联立式（22）、（23）得

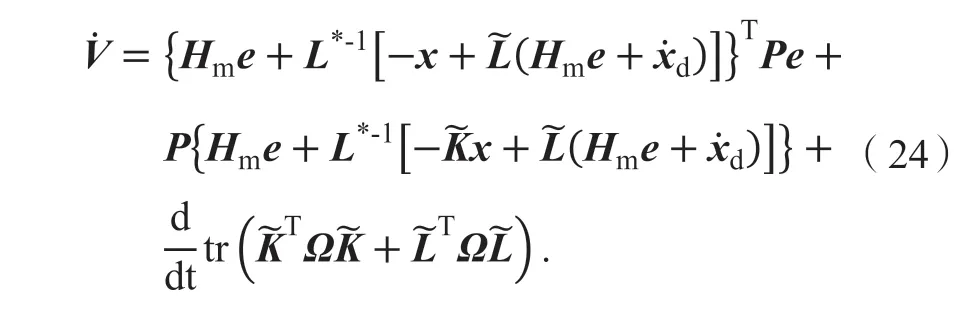
简化得

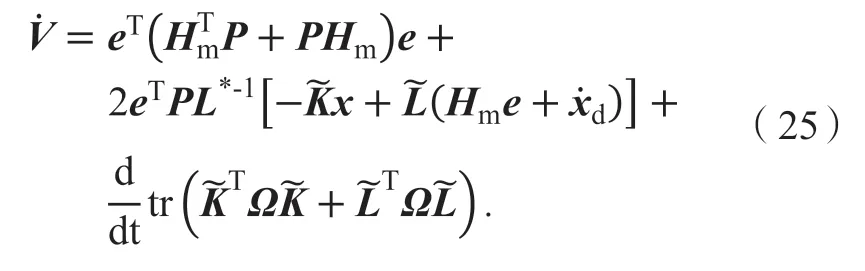
根据矩阵的迹的性质得

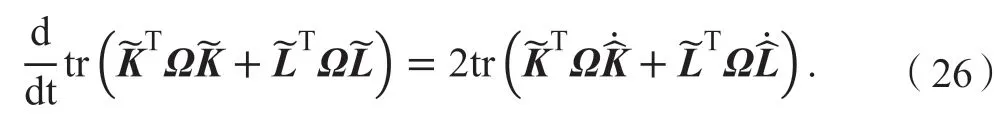
联立式（25）、（26）得

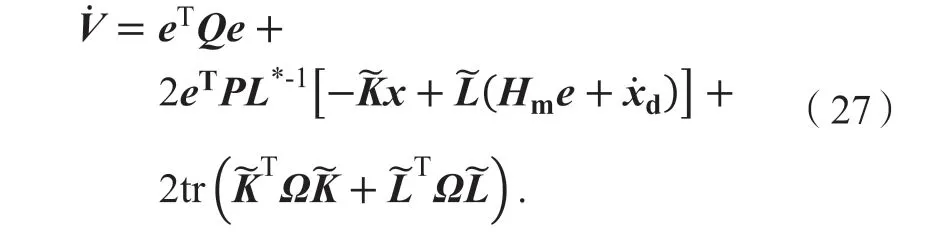
根据对称矩阵以及矩阵的迹的性质得：

联立式（27）、（28）、（29）得

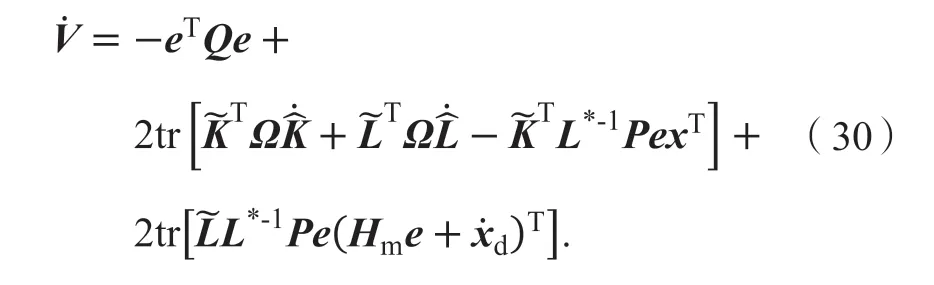
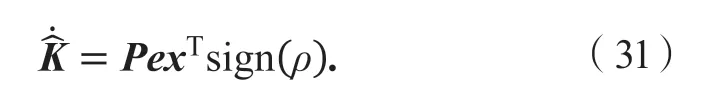
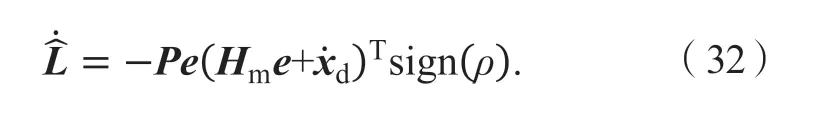
联立式（30）、（31）、（32），可得

由V≥0，且，可知控制输入和自适应控制率在有限时间内使得参数和状态量保持有界，跟踪误差接近于零，进而趋于稳定。这说明了本控制器满足稳定性要求。

3 下层控制器

在此节设计中，本文将上层控制器的输出力矩有效地分配至各个车轮，达到最佳分配效果，从而使车辆在行驶中更为稳定。其轮胎力作为车辆稳定性的重要参考因素，当轮胎利用率[27]达到最低时，其利用潜能越大。本文仅考虑对轮胎驱动效能的侧向力进行控制，目标函数可写为：

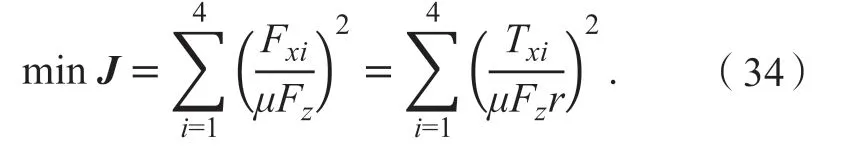
由δ较小，cosδ≈ 0，可得上层控制器输入变量ΔMz与总纵向力需求Fx的约束条件：

转变为矩阵形式为

式中：H为效率矩阵；Tw为左右轮距；r为车轮半径，其余见下式：

受轮毂电机最大转矩约束条件为

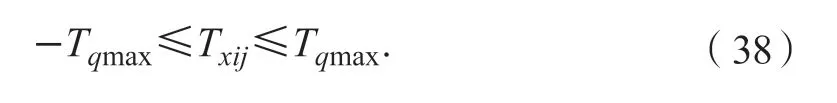
式中：Tqmax为轮毂电机最大转矩。

联立式（34）、（36）、（38）得标准二次型：

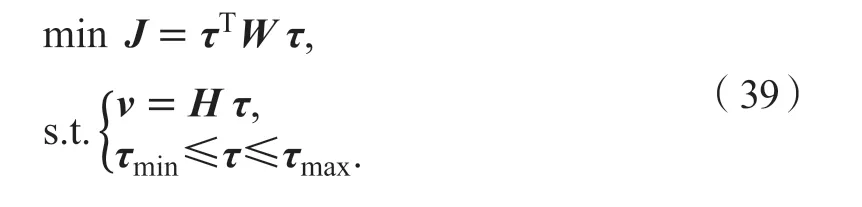
为最大限度地提高控制效果，以实现车辆行驶稳定性。本文利用二次规划法[28]进行目标函数求解，将上述MRAC力矩ΔMz分配到各个车轮，为简化步骤及减少运算时间，其优化目标函数可改为下式：

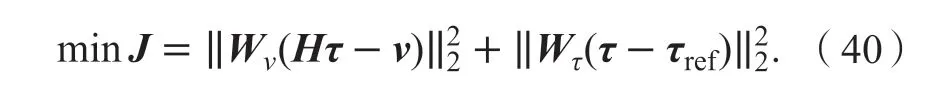
式中：Wv为分配需求权重矩阵，Wv= diag[1 1 1 1]；Wτ为控制向量权重矩阵，Wτ= diag[10 10 10 10]；τref=[0 0 0 0]T。

目标函数J中，以车辆稳定为目的，将目标函数值尽可能的降至最小。本文选用Matlab优化工具箱中的函数“ Quadprog ”求解器来实时计算最优的纵向力[29]。

4 Carsim与Simulink联合仿真验证

为验证上述算法有效性，利用Carsim与Simulink在高、低附工况下进行联合仿真验证。其双移线工况根据国际乘用车稳定性测试标准[30]而来。本文选取车辆参数如表1所示。

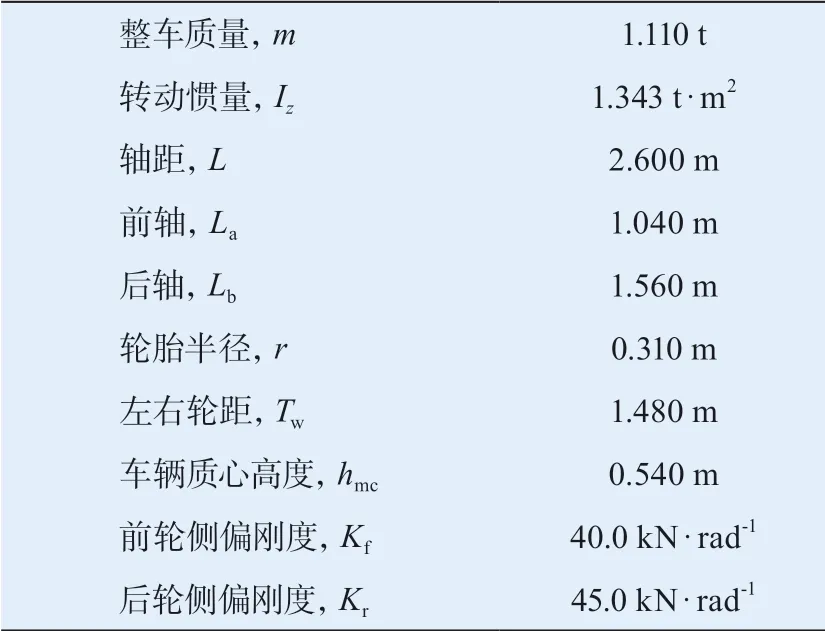
表1 车辆参数

4.1 控制器参数设置

由于对于控制器增益矩阵并无通用的调节技术，选择不同的Hm和P矩阵可对应产生不同的结果。为保证MRAC控制器的有效性，满足Lyapunov证明条件下，本文对控制器的参数进行标定得到一组合理的参数，其MRAC增益矩阵

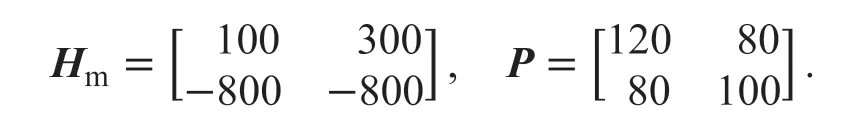
4.2 双移线工况（高附、低附）

本文分别在道路附着因数μ为0.85和0.40的工况下，以Vx= 80 km/h进行联合仿真。通过在无控制情况、SMC方法和MRAC方法下进行稳定性比较，其中SMC采用文献[31]中的滑模控制算法。仿真得横摆角速度、质心侧偏角、X-Y轴位移图以及横摆力矩图，如图3所示（图3在下页）。

如图3a所示：MRAC方法的横摆角速度在峰值上较SMC方法下降了17.1%、无控制状态下降了19.4%；MRAC方法的质心侧偏角在峰值上较SMC方法下降了34.5%、较无控制状态下降了54.8%；在期望轨迹上Y轴的峰值最小，波形更接近于参考轨迹；其所得横摆力矩的波形图也较SMC更为平滑。

如图3b所示：由于附着因数低，路面能够提供的附着力有限，车辆以Vx= 80 km / h的行驶过程出现一定的波动情况。对比SMC和无控制的效果中，在MRAC控制下有效地限制了ω与β的变化，其中ω在峰值上较SMC下降了7.1%、无控制状态下降了16.1%；β在峰值上较SMC下降了26.5%、较无控制状态下降了64.3%；在期望轨迹对比中，在MRAC下轨迹更符合驾驶意图，依旧表现出了良好的控制效果；同时，横摆力矩消除SMC了抖振，且所需峰值更低。为更加直观的量化控制器性能，本文使用平均绝对误差(mean absolute error, MAE)来评价。其计算公式为：

图3 不同附着条件下的状态量比较

式中：error为采样时间的跟踪误差值；n为样本数量。

通过计算可得在高低附工况下的横摆角速度、质心侧偏角以及X-Y位移轨迹的MAE值如表2所示。

表2 双移线工况平均绝对误差MAE

在高附工况下，所提出的MRAC与传统的SMC相比，跟踪横摆角速度ω、质心侧偏角β以及X-Y位移轨迹Dy的MAE分别降低了43.0%、37.1%和17.5%；在低附工况下，跟踪横摆角速度、质心侧偏角以及X-Y位移轨迹的MAE分别降低了25.3%、23.2%和12.5%。进一步说明了本文所设计的MRAC稳定性控制算法具有更好地控制效果。

5 结 论

本文针对车辆模型中系统参数不确定性的问题，设计了一种基于MRAC的横摆力矩稳定性分层控制算法。在上层控制器中，通过自适应律对车辆系统参数进行实时估计，获得期望的附加横摆力矩；在下层控制器中，考虑到轮胎利用率、电机最大扭矩输出约束以及道路附着力约束，利用二次规划对目标函数进行求解，将附加横摆力矩进行合理地分配至4个车轮，保证分配力矩的实时性。最后采用Matlab/Simulink与汽车动力学仿真软件Carsim进行联合仿真测试。

结果表明：本文所提出的MRAC控制算法与传统滑模算法相比，一方面克服了滑模算法带来的抖振，降低了质心侧偏角、横摆角速度以及纵向位移的大小；另一方面通过自适应律实时估计来抑制系统的不确定性扰动，改善了控制器的效能，进而提高了车辆行驶的安全性以及可靠性。

参考文献 (References)

[1] 余卓平, 冯源, 熊璐. 分布式驱动电动汽车动力学控制发展现状综述 [J]. 机械工程学报, 2013, 49(8): 105-114.

YU Zhuoping, FENG Yuan, XIONG Lu. Review on vehicle dynamics control of distributed drive electric vehicle [J].Chin J Mech Engi, 2013, 49(8): 105-114. (in Chinese)

[2] 宗长富, 郑宏宇, 田承伟, 等. 基于直接横摆力矩控制的汽车稳定性控制策略 [J]. 吉林大学学报（工学版） ,2008(5): 1010-1014.

ZONG Changfu, ZHENG Hongyu, TIAN Chengwei, et al. Vehicle stability control strategy based on direct yaw moment control [J].J Jilin Univ (Engi Tech Ed), 2008(5):1010-1014. (in Chinese)

[3] JIN Xianjian, YIN Guodong, LI Yanjun, et al. Stabilizing vehicle lateral dynamics with considerations of state delay of AFS for electric vehicles via robust gain-scheduling control [J].Asian J Control, 2016, 18(1): 89-97.

[4] Rubin D, Aroget S. Vehicle yaw stability control using active limited-slip differential via model predictive control methods [J].Vehi Syst Dyna, 2015, 53(9): 1315-1330.

[5] SHEN Huan, TAN Yunsheng. Vehicle handling and stability control by the cooperative control of 4WS and DYC [J].Modern Phys Lett B, 2017, 31: 19-21:

[6] 罗霜, 舒红宇, 姚泽杰, 等. 微型汽车操纵稳定性的人-车动力学耦合效应 [J]. 哈尔滨工业大学学报, 2018,50(1): 146-153.

LUO Shuang, SHU Hongyu, YAO Zejie, et al. Effects of human-vehicle dynamics interaction on the handling stability of miniature automobile [J].J Harbin Inst Tech,2018, 50(1): 146-153. (in Chinese)

[7] 唐毅, 刘卫宁, 孙棣华, 等. 考虑前后车辆综合效应的跟驰模型及其稳定性分析 [J]. 哈尔滨工业大学学报, 2014,46(2): 115-120.

TANG Yi, LIU Weining, SUN Dihua, et al. A new car following model with considering the synergy effect of ahead-backward vehicles and its stability analysis [J].J Harbin Inst Tech, 2014, 46(2): 115-120. (in Chinese)

[8] 中华人民共和国国家统计局. 2019年中国交通事故死亡人数统计 [EB/OL]. (2020-02-28), https://data.stats.gov.cn/easyquery.htm?cn=C01&zb=A0S0D01&sj=2020.

National Bureau of Statistics of the People’s Republic of China. Statistics on the number of deaths from traffic accidents in China in 2019 [EB/OL]. (2020-02-28),https://data.stats.gov.cn/easyquery.htm?cn=C01&zb=A0S0D01&sj=2020. (in Chinese)

[9] 宗长富, 代昌华, 张东. 智能汽车的人机共驾技术研究现状和发展趋势 [J]. 中国公路学报, 2021, 34(6): 214-237.

ZONG Changfu, DAI Changhua, ZHANG Dong. Humanrobot interaction technology of autonomous vehicles：A review and perspectives [J].Chin J Highway Transp,2021, 34(6): 214-237. (in Chinese)

[10] 余卓平, 肖振宇, 冷搏, 等. 分布式驱动电动汽车操纵稳定性控制评价体系 [J]. 华东交通大学学报, 2016, 33(5):25-32.

YU Zhuoping, XIAO Zhenyu, LENG Bo, et al. Control evaluation system testing of distributed drive electric vehicle handling stability [J].J East Chin Jiaotong Univ,2016, 33(5): 25-32. (in Chinese)

[11] 张利鹏, 李亮, 祁炳楠. 轮毂电机驱动电动汽车侧倾稳定性解耦控制 [J]. 机械工程学报, 2017, 53(16): 94-104.

ZHANG Lipeng, LI Liang, QI Bingnan. Decoupled roll stability control of in-wheel motor drive electric vehicle [J].Chin J Mech Engi, 2017, 53(16): 94-104. (in Chinese)

[12] 张细政, 郑亮. 基于转矩协调分配的分布式驱动电动汽车稳定性控制 [J]. 中国机械工程, 2018, 29(15): 1780-1787.

ZHANG Xizheng, ZHENG Liang. Vehicle stability control of distributed-driven electric vehicles based on optimal torque allocation [J].Chin Mech Engi, 2018, 29(15): 1780-1787. (in Chinese)

[13] 丁惜瀛, 李琳, 于华, 等. 电动汽车DYC/ASR变论域模糊集成控制 [J]. 汽车工程, 2014, 36(5): 527-531, +545.

DING Xiying, LI Lin, YU Hua, et al. Integrated DYC /ASR-based variable universe fuzzy control for electric vehicles [J].Automotive Engineering, 2014, 36(5): 527-531, +545. (in Chinese)

[14] 严运兵, 叶刚, 许小伟, 等. 基于模型预测控制的电动轮车辆横摆控制 [J]. 武汉科技大学学报, 2018, 41(3): 226-231.

YAN Yunbing, YE Gang, XU Xiaowei, et al. Yaw control for motor-wheel vehicle based on model predictive control[J].J Wuhan Univ Sci Tech, 2018, 41 (3): 226-231. (in Chinese)

[15] 李升波, 李克强, 王建强, 等. 非奇异快速的终端滑模控制方法 [J]. 信息与控制, 2009, 38(1): 1-8.

LI Shengbo, LI Keqiang, WANG Jianqiang, et al.Nonsingular and fast terminal sliding mode control method [J].Info Control, 2009, 38(1): 1-8. (in Chinese)

[16] DING Shihong, WANG Jiadian, ZHENG Weixing.Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions [J].IEEE Trans Indu Electr, 2015, 62(9): 5899-5909.

[17] Bianchi D, Borri A, Di Benedetto M D, et al. Adaptive integrated vehicle control using active front steering and rear torque vectoring [J].Int’l J Vehi Autonomous Syst,2010, 8(2-4): 85-105.

[18] DING Nenggen, Taheri S. An adaptive integrated algorithm for active front steering and direct yaw moment control based on direct Lyapunov method [J].Vehi Syst Dyn, 2010, 48(10): 1193-1213.

[19] HUANG Wei, WONG Pakkin, WONG Kain, et al.Adaptive neural control of vehicle yaw stability with active front steering using an improved random projection neural network [J].Vehi Syst Dyna, 2021, 59(3): 396-414.

[20] Baidu, An open autonomous driving platform [EB/OL].(2021-01-01), https://github.com/ApolloAuto/apollo.

[21] 陈龙, 解云鹏, 蔡英凤, 等. 极限工况下无人驾驶车辆稳定跟踪控制 [J]. 汽车工程2020, 42(8): 1016-1026.

CHEN Long, XIE Yunpeng, CAI Yingfeng, et al. Stable tracking control of autonomous vehicles at extreme conditions [J].Automotive Engineering, 2020, 42(8):1016-1026. (in Chinese)

[22] ZHANG Jiaxu, LI Jing. Integrated vehicle chassis control for active front steering and direct yaw moment control based on hierarchical structure [J].Transa Inst Meas Control, 2019, 41(9): 2428-2440.

[23] AO Di, HUA Xingqi, YU Guokuan, et al. Robust active post-impact motion control for restraining a second crash[C]//2020 IEEE 16th Int’l Conf Automation Sci Engi(CASE), Hongkong, China: IEEE, 2020: 159-164.

[24] Pacejka H B. Tyre and Vehicle Dynamics (2 Ed) [M].Oxford: Butterworth-Heinemann. 2006: 156-215.

[25] Doumiati M, Victorino A C, Charara A, et al. Onboard real-time estimation of vehicle lateral tire-road forces and sideslip angle [J].IEEE-ASME Transa Mech, 2011, 16(4):601-614.

[26] AO Di, WONG Pakkin, HUANG Wei, et al. Analysis of co-relation between objective measurement and subjective assessment for dynamic comfort of vehicles [J].Int’l J Automotive Tech, 2020, 21(6): 1553-1567.

[27] Mokhiamar O, Abe M. Simultaneous optimal distribution of lateral and longitudinal tire forces for the model following control [J].J Dyna Syst Meas Control:Trans ASME, 2004, 126(4): 753-763.

[28] LI Li, CHEN Xiqun, ZHANG Lei. A global optimization algorithm for trajectory data based car-following model calibration [J].Transp Res Part C:Emerging Tech, 2016,68: 311-332.

[29] LI Boyuan, DU Haiping, LI Weihua. Optimal distribution control of non-linear tire force of electric vehicles with inwheel motors [J].Asian J Control, 2016, 18(1): 69-88.

[30] ISO. ISO 3888-1, 2018. Passenger cars-test track for a severe lane-change manoeuvre-part 1: Double lane-change[S/OL]. (2018-12-18), https://www.iso.org/standard/67973.html .

[31] DING Shihong, LIU Lu, ZHENG Weixing. Sliding mode direct yaw-moment control design for in-wheel electric vehicles [J].IEEE Tran Indu Electr, 2017, 64(8): 6752-6762.