智能汽车的运动规划与控制研究综述

采国顺，刘昊吉，冯吉伟，徐利伟，殷国栋

（东南大学 机械工程学院，南京 211189，中国）

随着现代社会的不断进步与发展，人们对于出行安全性、便捷性和经济性等方面的需要越来越高。融合了车辆智能化、网联化和电动化等先进技术的智能汽车，在车辆行驶安全性与经济性方面具有巨大的优势，在世界范围内得到了广泛的关注[1]。

智能汽车利用车载传感器进行综合感知，具有自主决策能力，能够控制车辆安全，高效地行驶[2]，是实现未来交通的重要发展途径。从功能上划分，典型的智能驾驶主要包括感知、决策与规划、控制3个模块[3]，每个模块又可细分为不同的小模块，如图1所示。通过各模块之间的协调配合，实现特定条件下的智能驾驶，其中，综合感知层将传感器系统采集的数据进行处理与融合，实现车辆对环境、位置、交通、目标与障碍物、车辆状态等信息的精确感知；决策规划层根据综合感知和车辆状态信息，结合车辆与环境实际的空间和时间约束，输出车辆下一阶段驾驶行为与运动轨迹，是连接综合感知层与控制执行层的关键模块；控制执行层是依据轨迹规划模块输出的结果，对车辆期望动作进行实现并获取状态反馈信息[4]。决策规划层和控制执行层均是以车辆模型为基础展开研究，且其结果将直接决定车辆目标动作与实现效果，因此对行驶安全性与经济性起到关键影响。本文针对与智能汽车自车状态密切相关的运动规划与控制进行综述研究，梳理最新的研究进展，并给出发展趋势分析。

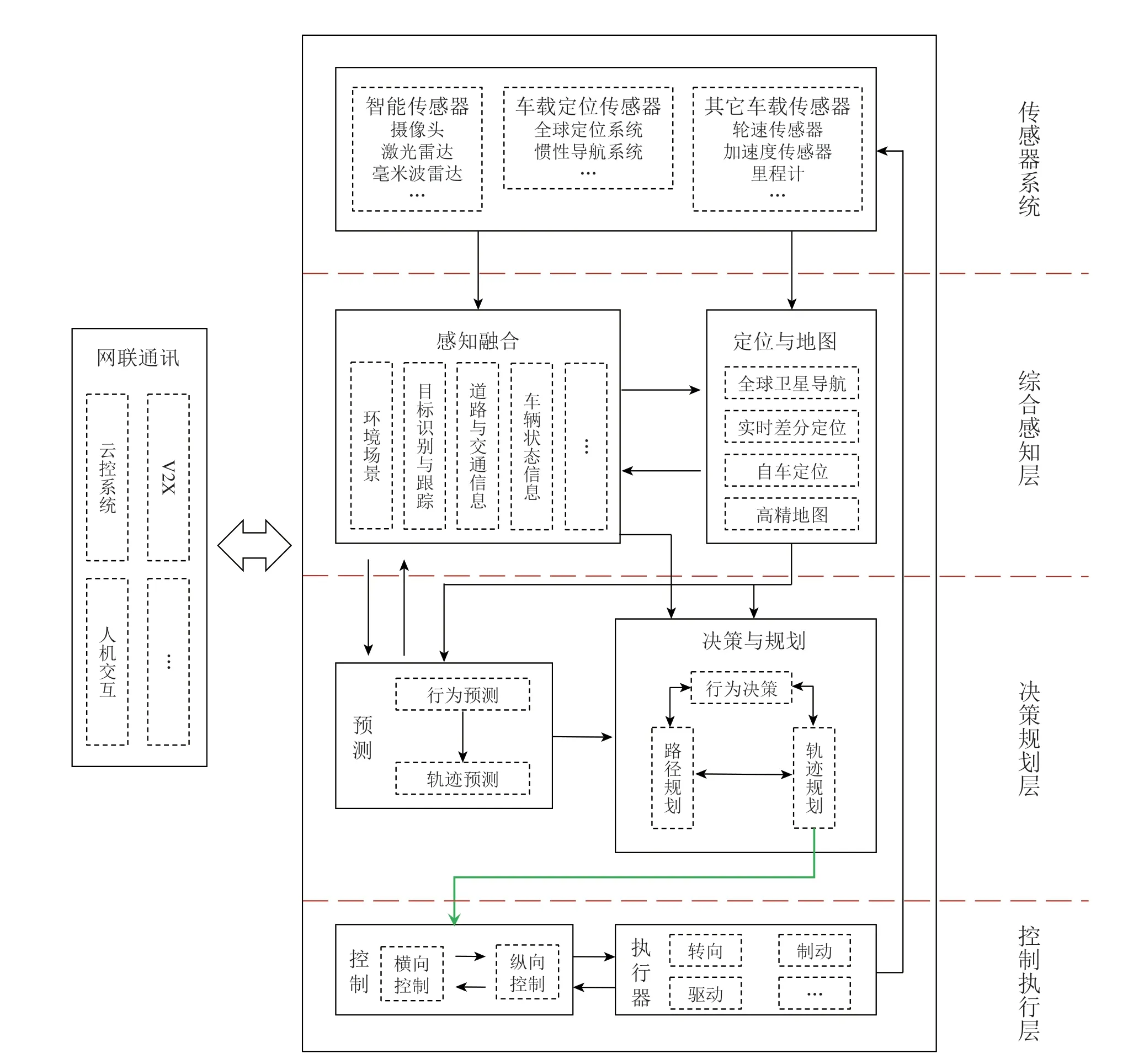
图1 模块化技术路线典型架构

1 运动规划

智能汽车决策与规划大致可分为路径规划、轨迹规划和行为决策这3大功能模块[5]，如图2所示。路径规划模块主要实现行程调度功能，其依据道路网络信息提供从初始位置到目标终点的总体长期规划。轨迹规划模块遵从风险评估、严格安全约束和驾驶目标优化，根据实时交通环境制定动态可行的运动轨迹。行为决策作为连接前两者的桥梁，可以存储当前和历史动态感知及车辆与外界的信息交互（vehicle to everything，V2X）数据，结合对自车周围所有目标物的状态预测和相应风险估计，决定车辆动作并传达路径和轨迹规划与修正需求。由于本文关注点在于车辆运动规划，而行为决策与车辆本体动作间无直接联系[6]，因此不属于本文研究要点。本节主要对路径规划和轨迹规划的研究现状进行综述。

图2 智能汽车决策与规划典型架构

1.1 路径规划

路径规划的基本思想是：基于多源感知信息，在保证前向安全的前提下，以一定的更新频率搜索抵达目的地的可行路径，并迭代选择出一条从起始点到终止点的目标最优路径[7]。路径规划在移动机器人领域得到广泛研究，发展出了图搜索、采样、智能算法等主要方法，并被迁移到车辆路径规划研究中以实现复杂路网环境下车辆最优行驶路径的制定。根据规划侧重点的不同，路径规划又可分为传统的路程最短路径规划和兼顾路程和能耗最优的经济性路径规划 （Ecorouting）[8]，其中后者更关注车辆本体动力与能效特性。本节将首先介绍车辆路径规划的常用方法，之后介绍经济性路径规划的近期研究进展。

1.1.1 图搜索算法

图搜索算法在已建模环境中通过连接节点生成可行路径。Dijkstra算法[9]是最为典型的一种单源搜索算法，通过将路网抽象为含有节点和带权边的网格图，并对从起始点到终点间不同可行路径的边权值进行累加和比对，可以寻找到总边权值最小的最短路径[10]。由于该算法对所有方向进行统一探索，因此可以寻找到全局最优路径，但其近乎遍历的搜索方式使得计算效率低下。

A*算法是一种启发式图搜索算法，其通过引入启发式代价函数，使得节点拓展更具有目的性，从而尽可能减少被搜索节点，实现相比于Dijkstra算法更为高效的运算求解过程[11]。启发式代价函数可以根据安全性和驾驶目标的差异构造成不同形式，如考虑车辆到车道边界的距离以及累计行驶距离[12]、考虑到目标点距离和危险运动惩罚值[13]等。D*算法是A*算法面向动态场景应用的改良算法，其遵循从终点向起始点反向搜索的方式，并引入后向指针记录拓展节点的母节点信息，当障碍物动态变化导致已规划路径不可行时，已经记录的后向信息可以被再次调用以避免重复计算，从而大大缓解求解负担[14]。总体而言，A*和D*算法可以有效减少图搜索算法的树分支和搜索量，在提供较好完备性的同时兼具求解效率提升。但该算法要求预先获取环境完整信息进行建模，且在高维复杂空间下仍会面对搜索维度灾难。

1.1.2 采样算法

基于采样的算法试图解决高维时序约束空间的路径规划问题，其以概率完备性取代搜索完备性，通过随机采样的方式探寻空间点之间的连通性[15]。最常用的基于采样的算法是概率路线图方法（probabilistic roadmap，PRM）[16]和快速探索随机树（rapidly-exploring random tree，RRT）[17]，前者主要是以随机散布采样点的方式生成可供路径搜索的环境，而后者则是一种兼具随机节点生成和路径搜索的算法。快速随机扩展树算法（rapidly-exploring random trees, RRT）可以对于未知环境区域执行随机搜索，允许在半结构化空间中进行快速规划，此外还具有考虑如车辆的最大转弯半径和动量等非完整约束的能力[18]。RRT算法已被拓展为Goal-bias RRT[19]、RRT-Connect[20]等双源搜索形式，并被证明是概率完备的，失效概率呈指数衰减。然而，RRT算法收敛到最优解的概率实际上为零[21]，因此又衍生出了RRT*算法。RRT*算法通过邻域节点重连步骤优化路径选择，是一种具有渐近最优性和概率完整性的采样式算法。Dijkstra、A*和RRT算法示意见图3。

图3 典型路径规划算法示意图[4]

1.1.3 智能算法

智能算法受自然现象启发得来，该类方法尝试模仿自然界中解决具有不精确性、不确定性和部分真实性复杂问题的思路，从而以较低的成本实现实用且稳健的解决方案[22]。人工神经网络（artificial neural network, ANN）是一种典型智能算法，其试图模仿人脑网络处理、记忆信息的方式，提供智能路径规划，可以在不了解系统及其环境的情况下，解决输入和输出呈非线性映射关系的问题[23]。模糊逻辑算法基于人脑的不确定性概念判断和推理思维给出了一种规则化的规划思想，运用隶属度的概念处理现象与动作之间的模糊对应关系，适用于环境模型信息不完整、不确定，或系统强非线性、大滞后的情况[24]。此外，遗传算法（genetic algorithm，GA）[25]、粒子群算法（particle swarm optimization，PSO）[26]、蚁群算法（ant colony optimization，ACO）[27]等智能算法也被应用到了物流运输和泊车路径规划研究中。

1.1.4 其他方法

人工势场法常用于精确道路模型已知情况下的避撞路径规划，该方法通过分别赋予起始点和目标点以高低势能，形成施加在自车奔赴目标点的引力，并给道路障碍物施加斥力，运用梯度下降法可以寻得安全可行路径[28]。为了避免引力与斥力相平衡导致陷入局部最优解的窘境，可以通过添加随机启发式函数的方式逃逸局部最小值[29]。但人工势场法由于不考虑车辆动力学，仍可能造成所规划路径不可行。插值曲线法既可以利用特定函数表达式独立生成路径[30]，也可以用作给定路径点集的平滑解决方案[31]，即可以在已知给定的描述全局路线点集的范围内，构建和插入新数据集以扩充路径点集，从而形成更平滑的路径，实现包含车辆约束和动态目标的连续性路径规划。此外，综合前文所述路径规划方法的混合路径规划研究也被广泛开展[32-33]，以达到取长补短的路径规划效果。

1.1.5 经济性路径规划

车辆学术界和工业界使用路径规划方法在寻找路程最短车辆行驶路径方面进行了诸多理论研究与落地应用。然而，随着社会对节能与环保的重视，研究热点逐渐由传统的路程最短路径规划转向更关注车辆本体动力和能效特性、兼具路程和能耗最优的经济性路径规划（Eco-routing）。经济性路径规划根据真实交通数据提取道路结构、拥堵情况和平均车速等特征信息，建立多源信息融合的路网-能耗耦合模型，并基于能耗最小目标搜寻全局最优路径[34]。利用考虑油耗权重的Dijkstra算法可以求解得到传统内燃机汽车的油耗最小路径[35-36]，类似地，若以二氧化碳最小化为目标，考虑动态时变的交通拥堵状况和时间窗口的影响，则可以滚动优化得到排放最少的行驶路径[37]。以上文献均关注于传统内燃机汽车的经济性路由问题，但是对于电动汽车而言，由于其具有制动能量回收的功能，其经济性路由问题与传统内燃机汽车相比，路由边权会出现负值，从而使得传统经济性路由的求解方法失效。为解决带有负边权的电动汽车经济性路由问题，需要重构带权有向图的节点与边使得传统路径规划方法可行[38]，或者直接使用改进算法对原始的带权有向图进行求解[39]。在此基础上，考虑到电动汽车续航能力有限，还可以车辆充电策略融入路径规划中，解决在固定时间窗约束下的电动汽车能耗最优路径规划问题[40]。

1.2 轨迹规划

轨迹规划层是在已知全局路径的基础上，结合实时车辆状态和动态道路交通环境信息，根据局部实际场景规划出一条包含空间位置-车速映射关系的时间序列点集或关系式[41]。根据研究对象划分，轨迹规划可分为单车自主轨迹规划和多车协同轨迹规划，前者常用方法包括模型预测控制、智能学习等，而后者主要包含最优控制、博弈理论、多智能体强化学习等方法[42]。本节将首先介绍单车自主轨迹规划，之后介绍多车协同轨迹规划。

1.2.1 单车自主轨迹规划

在动态交通环境中，车辆依据周围环境信息和自车驾驶需求，在满足车辆动力学限制和安全边界约束条件下自主规划行驶轨迹，可以实现单车安全、节能与高效驾驶。根据应用场景和驾驶需求差异，可以大致划分为以安全为首要考虑因素的轨迹规划，典型应用为变道超车和自主泊车，以及以能耗优化为主要目标的经济性轨迹规划，典型应用为经济性巡航驾驶和经济性信号灯控路口通行。

1） 安全导向的轨迹规划。对于以安全为首要考虑因素的轨迹规划，部分传统路径规划方法可通过增加时空耦合目标权重以及安全约束的方式进行重构并加以利用。如以分层轨迹规划的策略规避周围车辆，上层以采样规划的方式来确定安全可行操作，下层使用序列二次规划数值优化方法来优化局部轨迹[43]，如图4所示。但该类方法仍会面对复杂交通环境和驾驶需求带来的高维求解难题。模型预测控制（model predictive control，MPC）能够将车辆动力学和安全约束制定为有限范围约束，并可在考虑多优化目标的同时实现问题的有效求解，是用于解决车辆安全轨迹规划的主要方法[44]。为了应对不确定性模型摄动和环境扰动带来的影响，可以运用鲁棒MPC的方法解决。例如在自主变道超车问题中，利用面向结构化高速行驶环境的场景感知和轨迹规划框架，构建势场函数和安全可达区间，确定车辆的安全通行域，可以递归生成车辆横纵耦合抗干扰可行轨迹[45]。进一步地，运用MPC滚动优化思想，结合控制势垒函数（control barrier function，CBF）和控制Lyapunov函数（control lyapunov function，CLF）的轨迹规划策略也被提出[46]，该策略可以在满足复杂驾驶规则约束的同时，实现最优轨迹实时规划。同样是具有多约束非线性优化属性的泊车轨迹规划问题，可以采用基于内点法的动态优化策略解决[47]。此外，人工智能和机器学习方法也被用于轨迹规划研究中[48]。

图4 变道避障轨迹规划[42]

2） 经济性巡航驾驶。经济性巡航驾驶是实现车辆高效运行的一种节能纵向速度轨迹规划策略，被视为实现车辆节能减排的有效措施[49]。研究表明，前车匀速行驶时，加速-滑行（pulse-and-glide，PnG）操作在提高汽车节油效果上具有巨大潜力[50]。考虑地形因素和交通信息对车辆行驶的影响，以智能网联汽车技术和智能交通系统为应用背景，通过使用动态规划方法设计面向变坡度高速公路场景下的巡航策略，可以同时提高电动汽车的节能效果和电池寿命[51]。进一步地，采用滚动优化与迭代动态规划相结合的方法，可解决基于道路限速分段的电动汽车巡航轨迹优化问题[52]。该方法同样适用于存在弯道的巡航场景，研究表明在弯道上行驶时的最优行驶策略是车辆在入弯前减速、转弯时保持最优恒速，并在出弯时加速[53]。此外，为了在有其他车辆干扰的场景下实现经济性巡航效果，基于模型预测控制架构预测前车速度并做出相应规划，能够更好地提升车辆经济性驾驶性能[54]。

3） 经济性信号灯控路口通行。车辆在城市交通中可能会被交通信号灯中断正常行驶，这给经济性驾驶带来极大挑战。在智能网联环境下，车辆可依靠V2X技术获取或预测周围交通状况，利用获取到的交通信号相位和时序（signal phase timing message，SPaT）信息，依据经济性通行目标规划短期节能轨迹[55]。在此基础上，使用 SPaT信息开发的绿波通行系统（green light optimal speed advisory，GLOSA）可以最大限度地减少交叉路口的平均油耗和停车延迟[56]。考虑到交通信号的不确定性，可引入信号相位预测模型来确定绿色信号的概率，进而推导出最佳速度轨迹[57]。对于多个信号交叉口场景下的节能车辆轨迹规划，可以用准最优规则来得到实时应用的数值解[58]。上述研究通常假设车辆在自由流动的环境中行驶，然而，车辆的运行不仅取决于交通信号，还取决于进入交叉路口的前车[59]。针对此问题，往往需要考虑前车影响，通过车载传感器检测前方车辆的运动信息，结合前车安全约束，制定节能规划与控制策略优化能效目标[60-61]。此外，还可以利用V2X技术获取交叉路口车辆排队信息，将前方车辆队列长度作为自车轨迹规划的参考[62]，以考虑前向交通流的分层轨迹规划策略提升车辆在信号灯路口的节能水平[63]，如图5所示。

图5 经济性信号灯控路口通行场景[62]

1.2.2 多车协同轨迹规划

得益于智能网联汽车技术和智能交通系统的发展，基于车辆间信息共享和同步规划的多车协同轨迹规划技术得以被研究并应用。相比于单车自主轨迹规划，多车协同轨迹规划通过群体协同的方式，可以“由点到面”地改善交通出行状况[64]。由于多车协同轨迹规划与驾驶场景及需求间存在强耦合关联，需要针对具体情况做出策略上的适应性调整，因此本节将从匝道合流区通行、交叉路口通行等典型应用场景介绍多车协同轨迹规划。

1） 匝道合流区协同轨迹规划。匝道区域被视为典型的交通瓶颈区[65]，在该区域内，匝道与相邻主道间的车辆通过判断彼此运动状态调整自车轨迹，以产生适合于匝道车辆合流的车间距离和相对车速。由于驾驶员的预测存在误差及驾驶风格迥异，在这一交通瓶颈区往往会产生交通拥堵现象，造成额外的能源浪费，甚至会导致交通事故的发生，因此，匝道合流轨迹规划显得尤为重要[66]。匝道合流区多车协同轨迹规划被视为一种改善匝道行驶环境的有效手段，大体可被分为集中式协同规划策略和分布式协同规划策略[67]，如图6所示。

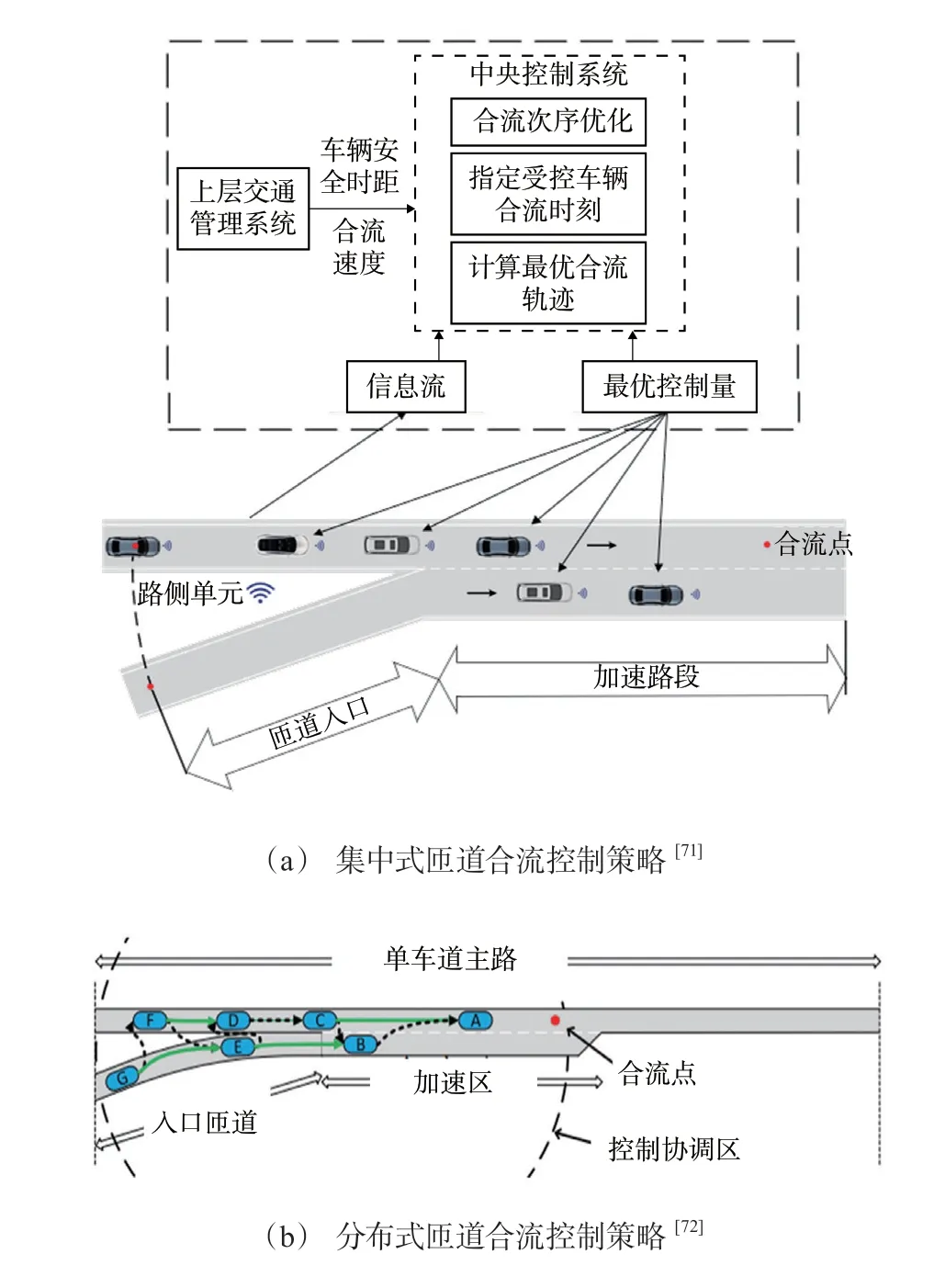
图6 匝道合流轨迹规划场景

在集中式策略中，合流区内的中央规划器以最小化全局代价为目标，规划每辆车的最优行驶轨迹。该问题往往被构建成一个具有起始点和终端合流点，并在限定匝道合流区域内控制状态变化的最优控制问题。最典型的做法是将集中式合流轨迹规划问题转化为无约束最优控制问题[68]，并利用极小值原理（Pontryagin’s minimum principle，PMP）给出闭式解析解。在此基础上，可以协同实现合流次序优化和轨迹规划，如基于规则的策略[69]，包含通行状态的改进动态规划策略[70]，或者是求解全局Pareto最优解的合作博弈策略[71]。虽然集中式策略可以获得全局最优解，但它可能会给系统带来很大的计算负担，尤其不利于大交通流量的场景。而与之相反地，分布式架构则具有更佳的灵活性、可拓展性和容错性。在分布式策略中，每辆车通过使用共享的交通信息，用车载轨迹规划器来规划自车轨迹。在该架构中，无约束最优控制方法依然可以得到有效的轨迹规划结果[72]，车辆间动态博弈的思想也被运用到问题求解中，并可采用零抑制二元决策图以高效规划最优合流轨迹[73]。考虑到状态和控制量混合约束，可以设计考虑多种严格约束的分布式匝道合流最优控制框架，并使用PMP内点法求解最优轨迹[74]。此外，综合集中式和分布式优势，可以采用一种组队形式的多车合流区通行策略，将多车通行问题归结为每个车队头车间的次序优化和轨迹规划问题，在提升运算效率的同时实现次序和轨迹同步优化[75]。

2） 城市交叉路口交汇区协同轨迹规划。交叉路口交汇区域具有4个正交行驶方向，存在直行和左右转向选择，研究该区域内车辆协同通行问题相比于匝道区域而言更具有挑战性。部分学者将该区域通行效率归结为路权分配的问题，以通过交汇区的次序来确定最优轨迹。基于位置预留的方案（reservation-based scheme）是一种典型的快速规划方案[76]。该方案将道路进行网格划分，单个网格在每个时间点只能被1辆车占用。车辆以发送占用请求的方法得到时空轨迹点，同时交通系统也会预留已被提前占用或正在被占用的点，并发送该信息给其他车辆以避免重复问询。当先进入控制区的车辆有网格占领优先权时，便形成了先进先出（first-in-first-out，FIFO）策略。上述基于规则式的方法虽然能够快速求解，但可能会偏离最优解[77]。混合整数线性规划是一种可以求解全局最优通行次序的优化方法[78]，其引入二元变量代表通行优先权，可以在保证全局最优的同时提升求解效率，但该方法仍会在车辆数量增多时遭遇组合爆炸的计算瓶颈，无法被实时应用。Monte Carlo树方法使用有限的规划时间来探索可能成为最佳解决方案的节点，在优化性能和计算灵活性之间保持良好的平衡[79]，但该方法往往只能得到近似最优解。为了在保证求解效率的同时求得全局最优解，一种考虑通行冲突关系的动态规划方法被提出，该方法的核心思想是将大规模全局优化问题转化为小规模多阶段优化问题，实现了计算复杂度从指数级到多项式级别的锐减[80]。除了以通行次序决定行驶轨迹的思路，部分研究则更关注轨迹规划本身。基于最优控制极小值原理，建立优化交通流量、车辆能耗或乘坐舒适性目标的路口通行问题，每辆车根据特定通行次序计算其到达交汇区域的时间，并遵循速度和动力学约束获得到达交汇区的行驶轨迹[81]。进一步考虑包含转弯的多信号灯路口通行问题，仍然可用极小值原理得到闭式解[82]，如图7所示。此外，清华大学团队运用强化学习方法围绕多车道交叉路口场景下的轨迹规划问题展开相关研究[83-84]。还有部分文献将次序优化和轨迹规划以分层结构同步实现，如上层以缓解交通密度作为目标，下层则在最小化期望车速偏差的同时规划轨迹保证行驶安全[85]。

图7 多交叉路口通行轨迹规划场景[82]

3） 其他多车协同轨迹规划研究。在多车协同泊车场景中，需要在时刻保证车车避撞和障碍物规避的严格安全约束基础上，实现最优轨迹的协同规划，如图8所示。该最优轨迹规划问题可被构建成分布式的最优控制问题，每辆车利用Gauss伪谱法和序列二次规划法等优化方法求解各自的轨迹[86]。同样也可以采用集中式多车协同平行泊车规划架构实现全局优化，以渐进约束动态优化方法保证轨迹安全可行[87]。

图8 多车协同泊车轨迹规划[87]

除了以上特殊交通场景的协同轨迹规划外，还有文献针对一般的、非危险的道路场景展开协同运动规划研究，通过不同的目标函数设定，可以在乘客舒适度、节能效率和交通流量等性能表现上做出改善。如在高速路行驶场景中，利用基于优先级的策略来协调多个车辆，将多车轨迹问题分解为一系列连续的单车轨迹规划子问题[88]，但该方法仅可得到局部最优解。而采用全局规划方法，如混合整数二次规划方法，则可以产生高速协同规划全局最优解[89]。考虑到行驶稳定性，可以构建一种考虑队列稳定性的多车协同鲁棒轨迹规划方法，在优化轨迹的同时保证良好的鲁棒抗干扰性[90]。

2 运动控制

运动控制是智能汽车研究领域的核心问题之一，是将意图转化为行为的过程。控制器参照动态规划的轨迹，结合实时获取的车辆当前状态参数，包括横纵向车速、加速度、横摆角速度、质心侧偏角等动力学控制关键参数，以兼顾安全性、经济性、舒适性等多指标综合最优为宗旨，按照既定的逻辑做出控制决策，并发送控制指令到驱动、制动和转向等系统的执行机构，实现对车辆位置、速度、姿态的精确控制。智能汽车的运动控制主要包含纵向控制和横向控制。纵向控制是通过对油门和刹车系统的控制，实现速度跟踪，主要包含自适应巡航、主动避撞等；横向控制是通过对转向系统和横摆力矩的控制，实现路径跟踪，主要包含车道保持、变道、转弯等。智能汽车运动控制典型架构如图9所示。

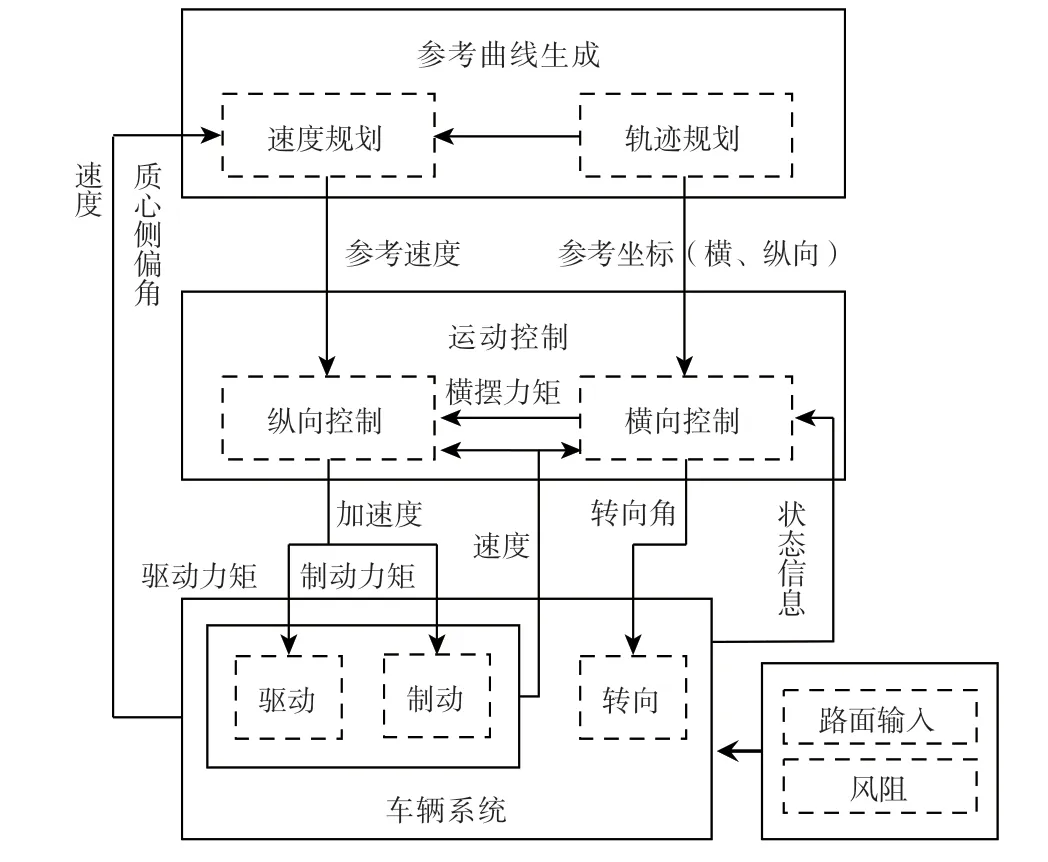
图9 智能汽车运动控制典型架构

智能汽车是典型的多输入-多输出系统，其内部存在复杂冗余执行特征和机-电-磁-网多域耦合非线性特性，以及明显的时滞现象，加之感知系统的准确度和精度仍有待提升[91]，为智能汽车在复杂多变的实际环境中实现精准运动控制带来了巨大的挑战。如何构建适用于智能汽车的控制系统框架和方法，以处理高度非线性问题、时滞问题以及感知受限问题，一直是智能汽车控制领域的难点和热点。

2.1 智能汽车纵向运动控制

智能汽车纵向运动控制是指通过对驱动和制动系统的控制，实现车辆自主速度跟踪，同时避免车辆纵向碰撞。传统汽车对于底盘安全性方面的研究已较为成熟，主要可通过制动防抱死系统和驱动防滑系统分别将纵向滑移率和滑转率控制在稳定区间[92]。当前智能汽车纵向控制的主要研究热点是在保证安全性前提下，实现对纵向速度的自适应调节。基于此，研究人员开发了自适应巡航控制（adaptive cruise control，ACC）及智能巡航控制（intelligent cruise control，ICC），并将其运用于不同等级的智能驾驶研究[93]。

自适应巡航控制 （ACC） 是对定速巡航的功能升级，系统通过控制驱动和制动系统，实现与前方车辆保持一定的空间间距。间距策略设计是ACC系统的核心，主要分为恒定空间策略和动态空间策略[94]。恒定空间策略即保持与前车恒定的空间间距[95]，而动态空间策略是根据车速变化，动态调整纵向车辆间距。根据底层运行机制的不同，动态空间策略又可分为时间间距策略[96]、交通流稳定性间距策略[97]、恒定安全系数间距策略[98]和人类驾驶行为间距策略[99]， 其中，时间间距策略如图10所示。

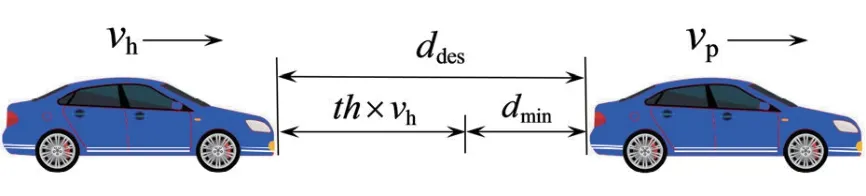
图10 ACC时间间距策略示意图[100]

随着车载通讯能力的提升，为了进一步提升驾驶安全、道路容量和经济性，协同自适应巡航控制（cooperative adaptive cruise control，CACC）越来越受到关注。CACC是指具有通信能力的智能汽车之间通过信息交互实现单一车辆或队列的自适应巡航行驶[101]，其中同质队列车辆通讯方式如图11所示。常用的通信协议有专用短程通信技术（dedicated short range communication，DSRC）、长 期 演 进 技 术（long term evolution，LTE）和第5代移动通信技术（5th generation mobile communication technology，5G） 等[102]。当 前CACC处于起步阶段，仍有许多问题亟待进一步解决和完善，如通讯时延[103-104]、通讯故障[105]、数据注入[106]、网络攻击[107]、功能降级[108]等。

图11 同质队列信息拓扑方式[104]

虽然ACC与CACC在实现车辆自适应速度调节的同时，会设置安全保障机制，但考虑到行驶安全是智能汽车最首要的任务，因而有必要设置冗余系统，进一步保障行驶安全性，因此，考虑面向行驶安全的主动避撞系统（collision avoidance，CA）得到迅速发展。纵向主动避撞系统通过传感器实时检测与前车距离，并在达到触发条件后通过主动制动防止碰撞发生[109]。CA是以防止碰撞为唯一任务，因而控制系统简单、稳定，但优先级最高[110]。此外，为提升综合行驶性能，有学者提出融合ACC/CACC与CA 的纵向控制方法[111]。

虽然对于巡航控制，主动避撞等控制策略的研究已取得一定进展，但如何将这些策略与车辆底层执行系统进行融合，仍有待进一步研究。总体来看，根据融合控制架构的区别，可将智能汽车纵向控制分为直接式和分层式控制[112]。直接式控制架构是基于纵向速度自适应调节策略，综合考虑纵向滑移率和滑转率、能耗最优目标，以及乘客舒适性等要求，直接输出控制执行器动作的指令，如驱动/制动力矩分配等。直接式控制研究方法主要有多目标综合优化方法[113-114]、 神经网络方法[115-116]等。直接式控制的优势在于可方便地进行多目标综合分析，得出最优化的控制输出，但缺点在于计算量较大，实时性难以保证。考虑到智能汽车纵向控制涉及多种不确定因素的影响[117]，如轮胎纵向滑移率和滑转率，动态目标和障碍物的实时变化，以及车辆实时状态的波动等，为兼顾控制性能和实时性，有学者提出分层式控制架构用于智能汽车纵向控制[118-119]。当前的分层式控制架构多是将纵向控制分为上层策略层和下层执行层，如图12所示。上层主要根据多性能指标设计控制策略，输出期望加速度或期望驱动/制动力矩[120-121]；而下层主要是根据上层控制输出，设计扭矩分配策略与执行器控制策略，控制驱动与制动系统运行[122-123]。

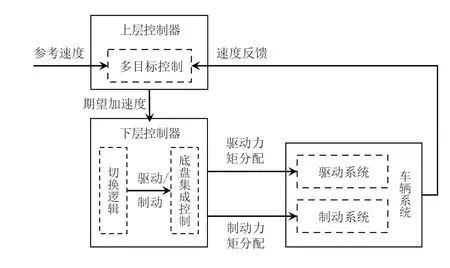
图12 分层式纵向控制架构简图

分层式控制架构相比直接式控制架构，具有灵活度高，实时性好等优势。如何做好策略层与执行层之间的协调与融合，是分层式控制架构的关键。为了应对高级别智能驾驶的发展需求，设计融合ACC/CACC/CA等控制系统的上层策略层亦是需要重点关注的地方。

2.2 智能汽车横向运动控制

车辆本身具有典型的非线性时变特性以及参数的不确定性（如车辆载荷、轮胎侧偏刚度以及地面附着系数等参数的变化），随着车辆智能化程度的提升，驾驶人逐渐脱离驾驶控制环，导致车辆控制自由度变大，驾驶精度要求越来越高，因此, 如何建立高效合理的横向稳定控制策略已经成为车辆控制领域研究的重点[124-125]。传统车辆的横向控制问题主要表现在横摆稳定性（主要参数指标为横摆角速度）以及轨迹跟踪精度（主要参数指标为质心侧偏角）两个方面。随着车辆控制需求的不断提高，横向控制方法的研究呈现螺旋式发展，从经典控制理论开始，过渡到以状态空间方程的现代控制理论，逐步发展到基于复杂非线性系统的智能控制理论。当前应用于车辆控制领域的算法主要有：经典控制理论的反馈与比例、积分、微分（proportion、integral、differential，PID） 控制方法[126-128]，现代控制理论的最优控制[129]、鲁棒控制[130]、模型预测控制[131]、自适应控制[132]、滑模变结构控制[133]等方法以及智能控制理论的模糊控制[134]、神经网络控制[135]等方法。由于PID控制具有适应性广、实现简单、无需建立模型的优点，已经在工程上得到广泛应用。但车辆转向运动是横向和横摆运动的多状态系统，当车辆纵向速度变化明显时，往往造成系统参数变化，单纯的PID反馈控制难以适应多输入多输出系统以及时变系统的控制需求。

针对PID控制无法解决多目标优化问题，众多学者提出了最优控制理论。针对受约束情况下车辆转弯过程中的最优控制问题，通过设定合适的参数对系统时延和一阶系统行为进行补偿，将安全性和舒适性的物理约束纳入控制器设计，并将最大横向加速度和变化率作为系统约束，实现了车辆的稳定控制[136]; 为了提高弯道上的车道保持性能，设计了增广观测器，估计了车辆状态和扰动，改进了电动助力转向（electricpower steering，EPS）系统存在的扭矩无法联合的问题，提出了考虑横向偏移量和向下偏移量的线性二次状态反馈控制方法[137]。最优控制可在模型精确的前提下实现控制目标最优，但由于车辆本体的非线性特性（部件间的连接间隙等）和时变外部激励（随机路面谱密度等）的影响，导致车辆系统的关键参数存在一定程度的不确定性，完整的车辆动力学特性难以精确表征。如车辆在高速大曲率转向工况下，车轮载荷变动导致的轮胎侧偏刚度变化明显，如图13所示。

图13 轮胎侧偏刚度变化[138]

针对车辆的参数不确定性问题众多学者采用鲁棒控制方法对车辆的横向控制方法进行研究。在车辆的路径跟踪以及换道控制中，采用鲁棒控制器设计了车辆横向控制系统，考虑了不同驾驶员特性、路面激励、延迟时间、预瞄时间和转向比例增益等因素，构造基于Lyapunov渐进稳定性的线性矩阵不等式，应用极点配置法提高了控制器性能[139-140]，验证了速度波动、道路附着系数变化和风阻的鲁棒性。根据反馈跟踪特性和抗扰性要求选择权重函数矩阵，综合考虑轮胎侧偏刚度以及通信时滞的影响，提出一种具有内在平衡的µ综合新方法[141]，其控制效果接近于最优控制方法，但控制器阶数有效减少，满足智能车辆的控制需求，µ综合控制架构如图14所示。由于鲁棒控制方法采用离线处理数据求得最优解，其具有较高的控制实时性，但对复杂多变的行车环境的适应性较差，且无法满足多复合约束下的实时在线优化控制的需求。

图14 µ综合控制架构[141]

为了满足实时在线优化控制需求，提高多约束条件下的车辆稳定控制性能，模型预测控制方法也被大量应用到车辆的横向控制中，模型预测控制采用当前时间的控制量作为控制输入，通过滚动迭代的方法不断更新优化区间，反复计算最优输入值，保证车辆横向运动过程中实时求解，其中模型预测控制原理框图如图15所示。在车辆主动安全控制中，基于Pareto 优化理论建立多智能体控制架构，构建车辆主动转向和横摆力矩融合的终端约束条件，应用模型预测控制方法设计车辆横向控制器，实现了车辆的主动安全控制[142]；同时该方法应用于车辆的换道和车道保持系统中[143-144]，通过设计凸优化的路径生成器生成了无碰撞轨迹，同时将模型预测控制转化为二次规划问题进行求解，建立8自由度车辆模型与Dugoff轮胎模型进行仿真验证。虽然模型预测控制能够满足多约束的控制需求，但是非线性系统的优化求解量非常大，难以保证在控制周期内实现高效控制运算。如何进一步提高算法的实时性，仍然是模型预测控制研究的重点和难点。

图15 模型预测控制原理框图

在车辆横向控制中，除了参数的不确定性和多约束空间外，车辆系统内部的时滞和外部干扰也会对车辆系统的性能产生重要的影响。为解决多时滞-干扰下车辆控制问题，自适应控制方法被应用于车辆的横向控制系统。自适应控制可根据被控对象的输入实时在线调整控制器参数，从而使系统运行处于最优或次优的状态，保证了车辆横向控制的精确性。在换道超车、车道保持以及人机协同的控制中，采用自适应控制理论设计车辆横向控制系统[145-147]，通过简化复杂动力学模型，采用学习模型预测控制理论构建车道偏离防范（lane departure prevention，LDP）控制器，实现了车辆横向运动的自适应调节，改进的自适应车道保持控制器的闭环系统架构如图16所示。为了更好地应对大数据学习的控制效果，神经网络控制方法被引入到横向控制中[148-150]，主要基于循环神经网络模拟自动驾驶汽车转向控制技术，研究缺乏精确模型信息的车道保持系统，利用深度学习及数据融合技术，精确预测车辆运动状态，实现横向稳定控制。虽然神经网络控制方法能够实现车辆的横向控制，然而其对数据量和计算能力的需求较高，实时性难以有效保证。

图16 改进的自适应车道保持控制器的闭环系统架构[145]

为解决智能车辆内在的高维强耦合，内部作用机理复杂难表征等问题，模糊控制方法被应用到车辆横向控制中，实现车辆的路径跟踪、变道以及横向稳定控制等。基于高精度GPS和无线网络环境提供的信息，模糊控制能够模仿人类在超车时的行为和反应[135]，且可模拟步进转向工况和正弦转向工况下前轮的横摆角速度和侧偏角情况[151]，有效地提高了系统运行效率。在主动前轮转向（active front steering，AFS）与直接横摆力矩控制（direct yaw control，DYC）集成稳定控制中将非线性刷子轮胎动力学和纵向速度的非线性函数通过T-S模糊方法建模，然后利用多模糊规则得到不确定的非线性车辆横向动态T-S模糊模型。采用并行分布补偿策略和假定变量设计模糊鲁棒状态反馈控制器，并通过构建一组满足Lyapunov渐近稳定性和二次鲁棒性能的线性矩阵不等式进行求解[152]，AFS和DYC组合的车辆模糊控制系统体系结构如图17所示。

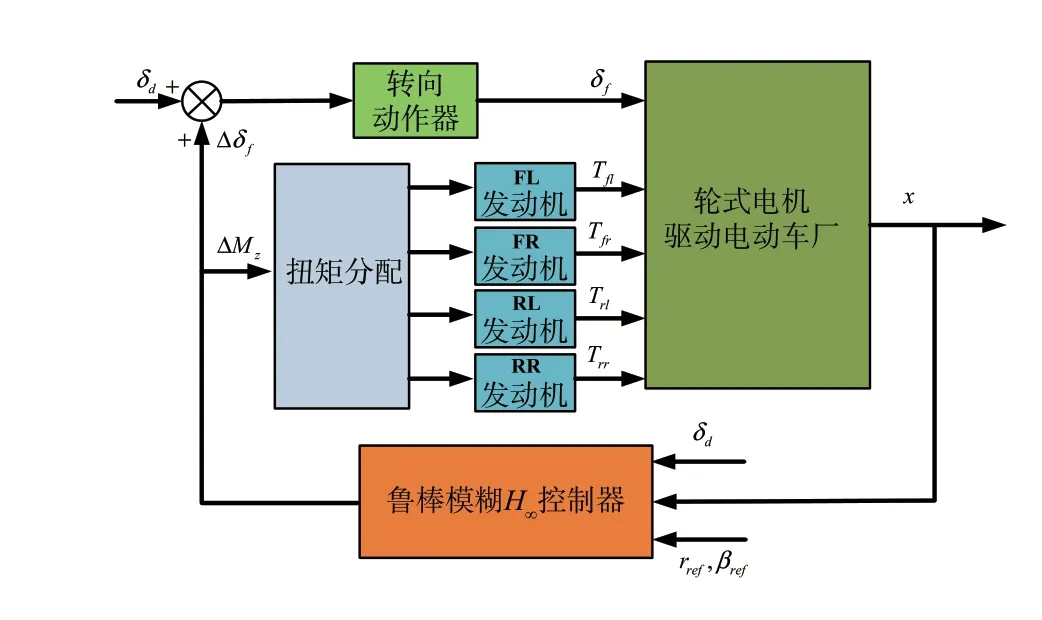
图17 AFS和DYC组合的车辆模糊控制系统体系结构[152]

滑模变结构控制是一类特殊的非线性控制，其非线性体现在控制过程的不连续。滑模变结构控制的主要优点是使得控制对扰动不敏感，响应快速能够有效处理车辆的路径跟踪控制问题[153]；此外，众多学者对一些方法进行尝试，如自抗扰控制方法[154]，其控制器实时估计车辆的不确定性和外部干扰，并对其进行主动补偿，基于Lyapunov稳定性分析表明，控制系统在平衡点附近呈指数稳定；反步控制和前馈控制方法[155]，其解决了一类非线性欠驱动系统的渐近镇定问题；神经网络PID控制方法[156]，其使用遗忘因子递推最小二乘估计法（recursive least square estimation of forgetting factor，FFRLS）识别系统参数，基于车辆模型和转向系统模型建立神经网络PID控制器进行横向路径跟踪控制，能够达到良好的控制效果。

2.3 智能汽车横纵向综合控制

由于车辆横纵向运动之间存在相互耦合特性，如运动学耦合，轮胎力耦合与载荷转移影响等[157]，相较于横纵向控制独立设计，采用综合控制策略可以有效避免耦合冲突，提高综合控制效果[158]。本文仅针对智能汽车路径跟踪与速度跟踪的综合控制进行探讨，关于执行层之间的横、纵向集成控制，可参见相关研究[159]。

根据控制架构的不同，可将智能汽车横纵向综合控制分为协同式综合控制和耦合式综合控制[112]。

协同式综合控制指的是未建立横纵向耦合动力学模型，横、纵向控制算法根据各自模型进行独立设计，通过设置状态交互来协调横纵向运动控制。此方式优势在于无需建立复杂模型，求解效率高，实时性较好，且系统构造较为灵活，易于实施。因此，协同式综合控制架构在考虑强非线性动力学特性的研究[160]，结合V2X通讯优势的研究[161]，以及在多车队列控制的研究[162]等均有成功应用。但由于没有对横纵向耦合机理进行深入探究，不能全面地反映真实的横纵向运动的之间的关系，因而会在某些情况下出现控制性能退化[163]，如大转向角、连续弯道或车速快速大幅波动等。

耦合式综合控制指的是根据横、纵向耦合动力学模型进行控制算法设计，可较为真实地反映车辆横纵向之间强耦合、非线性的物理关系。该方式能够获得较高的控制精度，但对硬件计算能力要求较高。常用的7自由度整车动力学模型，包含横向、纵向、横摆以及4个车轮的转动，如图18所示。

图18 7自由度车辆动力学模型[164]

针对耦合式综合控制，根据智能汽车驱动形式、底盘横纵向执行器的不同，研究人员开发了适用于不同车辆硬件配置的横纵向综合控制系统，如针对四轮独立驱动电动汽车[165]、结合主动转向控制[166]，直接横摆力矩控制[164,166]等。随着V2X技术的进步，智能汽车在复杂交通环境的预期表现也随之提升，耦合式综合控制对车辆控制性能提升明显的优势显得更加突出[167]，且对多车队列控制性能的提升也有帮助[168]。此外，神经网络[169]，脑机控制[170]等先进技术在提升耦合式综合控制性能中的成功应用也被陆续报道。

总体来看，随着智能汽车应用场景逐渐向通用化场景发展，横纵向综合控制的应用将会愈发受到重视。无论是采用协同式综合控制架构，或是耦合式综合控制架构，控制性能与实时性都将是需要重点考虑的方面。

3 智能汽车运动规划与控制发展趋势

智能汽车运动规划与控制技术取得了长足的发展，但随着汽车智能化的不断提升，对控制精度和实时性的要求日益增长。感知系统的增强使得信息获取更加丰富和及时，对运动规划与控制而言则是机遇和挑战并存；先进的通信技术在车用领域的广泛应用也对运动规划与控制产生了影响；且车辆动力学系统本身存在着大量非线性、强耦合特性，以及多源时滞异构现象。因此，如何解决上述问题并构建适用于智能汽车的运动规划与控制系统框架和方法，仍有待进一步研究和突破。对未来可能发展方向的初步展望如下：

3.1 运动规划领域

a） 考虑更为真实的动力学模型和实际约束：随着车辆运动规划研究的深入，对于车辆模型和约束的简化已成为制约规划性能提升的瓶颈所在。为了进一步释放规划方法对车辆性能的提升潜力，需要引入更为真实的动力学模型和实际约束，以在复杂动态环境中保证性能优越性和鲁棒性。

b） 考虑通讯损失和网络安全影响：多车协同运动规划在很大程度上基于V2X通信，但这容易受到诸如时间延迟和数据包丢失等通信障碍的影响。此外，干扰、V2X数据注入和车辆传感器操纵等网络攻击也会损害多车协同系统的性能。因此设计应对通讯损失和网络风险的强鲁棒抗干扰规划技术至关重要。

c） 考虑混合交通场景下的应用：现有研究中的大多数文献都仅围绕只有智能网联汽车的场景展开研究，但是由于技术和成本限制，多种类型车辆（智能网联车辆，智能车辆，网联车辆，传统人为驾驶车辆）共存的混合交通场景势必会存在很长一段时间。考虑到环境中其他车辆类型导致的不确定性，适用于纯智能网联车环境的协同规划策略不一定适用于混合交通环境。因此，解决混合交通场景下多源不确定性扰动共存的多车协同规划问题急需开展进一步研究。

3.2 运动控制领域

a） 融合多源感知信息的参数估计方法：多源感知信息为车辆动力学重要参数估计提供了新的选择，可充分利用环境、道路与交通信息，开发适用于智能汽车的参数估计体系，获取更准确的动态实时参数，提升车辆动力学控制性能。

b） 融合环境预知信息的综合控制技术：感知信息的提前预知，将促进预见控制技术发展。如何准确构建融合感知信息的横、纵向综合控制系统，结合车辆非线性、多耦合特性，建立耦合与解耦机制，并考虑时滞补偿，仍需要进一步探索。

c） 兼顾控制性能与实时性的多模型集控制：智能汽车为适应复杂多变的现实环境并满足实时性要求，往往需要使用多种控制策略与模型。如何构建横、纵向综合控制模型集，并确定合适的切换策略，将是实现实时动态控制的关键问题。

d） 基于车路协同技术的多目标综合协同优化控制：车路协同技术发展将促进智能汽车运动控制与多车协同控制进一步发展。如何利用先进通信技术处理智能汽车与多车队列、智能交通系统，以及电网系统的信息交互，并考虑通信时滞、网络安全等问题，实现多目标综合协同优化控制，将是需要重点突破的方向。

4 结 论

智能汽车的研究和发展将促进汽车工业与智能交通领域的转型和升级，为人类出行与社会生活带来革命性的变化。运动规划与控制技术作为提升智能汽车综合行驶性能的关键所在，仍将是长期热点研究方向。本文介绍了智能汽车路径规划、轨迹规划与横、纵向控制的研究现状，提出智能汽车运动规划与控制领域未来发展的方向为：规划领域需考虑更为真实的动力学模型和实际约束，考虑通讯损失和网络安全影响，以及考虑混合交通场景下的应用；控制领域需研究融合多源感知信息的参数估计方法，融合环境预知信息的综合控制技术，兼顾控制效果与实时性的多模型集控制，以及基于车路协同技术的多目标综合协同优化控制。