关于Diophantine方程(36n)x+(323n)y=(325n)z的整数解

常 青，高 丽

(延安大学 数学与计算机科学学院，陕西 延安 716000)

指数型Diophantine方程是Diophantine方程中比较有意义且较难的一类方程,给定正整数a,b,c,Diophantine方程ax+by=cz,x,y,z∈N的求解一直以来都是一个重要的课题。设a,b,c是商高数组,即a,b,c是满足a2+b2=c2的两两互素的正整数,则Diophantine方程

(na)x+(nb)y=(nc)z

(*)

显然有整数解(x,y,z)=(2,2,2)。1956年,Sierpinski[1]证明了当n=1,(a,b,c)=(3,4,5)时,方程(*)仅有正整数解(x,y,z)=(2,2,2);Jesmanowicz[2]证明了当n=1,(a,b,c)=(5,12,13),(7,24,25),(9,40,41),(11,60,61)时,方程(*)仅有正整数解(x,y,z)=(2,2,2),并且猜测对任意的正整数n,方程(*)仅有正整数解(x,y,z)=(2,2,2),这就是著名的Jesmanowicz猜想，又称为商高数猜想。目前有许多数学爱好者对它的研究已经取得了不少成果[3-10]。基于对以上文献的研究，本文主要运用简单同余法、奇偶分析法、二次剩余理论以及分类讨论等初等方法,证明了对任意的正整数n,当(a,b,c)=(36,323,325)时Jesmanowicz猜想成立,即Diophantine方程(36n)x+(323n)y=(325n)z仅有正整数解(x,y,z)=(2,2,2)。

1 相关引理

引理1[11]若z≥max{x,y},且正整数a,b,c(不一定互素)满足a2+b2=c2,则Diophantine方程ax+by=cz仅有正整数解(x,y,z)=(2,2,2)。

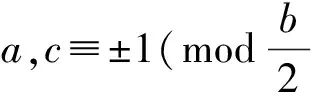
引理3 Diophantine方程36x+323y=325z仅有正整数解(x,y,z)=(2,2,2)。

证明因为36=22×32,323≡1(mod2),

325≡-1(mod2),

所以由引理2知,36x+323y=325z仅有正整数解(x,y,z)=(2,2,2)。

2 定理及其证明

定理对任意的正整数n,Diophantine方程

(36n)x+(323n)y=(325n)z

(1)

仅有正整数解(x,y,z)=(2,2,2)。

证明根据引理1，只需证明(1)式在n≥2且min{x,y}

情形1y

323y=nz-y(325z-36xnx-z)

。

(2)

由于y

设n=17u19vn,u+v≥1,gcd(n,323)=1,此时(2)式可化为

17y19y=17u(z-y)19v(z-y)n1z-y·

(325z-36x17u(x-z)19v(x-z)n1x-z)，

(3)

由此可见,n1=1。

情形1.1 若n=17u(u≥1),则y=u(z-y)。于是(3)式可化为

36x17u(x-z)=325z-19y，

(4)

对上式两边同取模8,模17,则有

(-3)z≡3y(mod8);2z≡2y(mod17)。

则y与z奇偶性相同，因此

y≡0(mod4),z≡0(mod2)。

令z=2z1,y=4y1,则由(4)式得

22x32x17u(x-z)=(325z1-192y1)(325z1+192y1)

，

(5)

这里gcd(325z1-192y1,325z1+192y1)=2,

由4|(325z1-192y1)知,23x-1|(325z1-192y1),

又3|(325z1-192y1),则

23x-1-32x|(325z1-192y1),

但23x-132x>23z134z1=648z1>325z1-192y1不成立。

所以(5)式没有整数解。

情形1.2 若n=19v(v≥1),则y=v(z-y)。于是(3)式可化为

36x19v(x-z)=325z-17y，

(6)

对上式两边同取模4,模19,则有

1≡(-3)y(mod4),y≡0(mod2);

2z≡(-2)y≡2y(mod19)，

得2(y-z)≡1(mod19)。

则y与z奇偶性相同。

若y≡z≡0(mod4),令z=4z1,y=4y1,则由(6)式得

22x32x19v(x-z)=(3252z1-172y1)(3252z1+172y1)。

(7)

注意这里gcd(325z1-17y1,325z1+17y1)=2,

由4|(325z1-17y1)知,23x-1|(325z1-17y1)，

又3|(325z1-17y1),则23x-132x|(325z1-17y1)。

但23x-132x>(24)2z1(33)2z1=4322z1>3252z1-172y1。

所以(6)式没有整数解。

若y≡z≡2(mod4),

令z=4z1+2,y=4y1+2,且y1,z1为奇数,则由(6)式得

22x32x19v(x-z)=

(3252z1+1-172y1+1)(3252z1+1+172y1+1)。

(8)

因为4|(3252z1+1+172y1+1),

3|(3252z1+1+172y1+1),

所以23x-132x|(3252z1+1+172y1+1)。

但23x-132x>24(2z1+1)33(2z1+1)=4322z1+1>

(325+17)2z1+1>3252z1+1+172z1+1>3252z1+1+172y1+1。

所以(6)式没有整数解。

情形1.3 若n=17u+19v(u≥1,v≥1),则

y=v(z-y)。

于是(3)式可化为

17y19y=17u(z-y)19v(z-y)·

(325z-36x17u(x-z)19v(x-z))，

(9)

则y=u(z-y)=v(z-y),

于是(9)式可化为

36x17u(x-z)19v(x-z)=325z-1。

(10)

对(10)式取模19,有2z≡1(mod19),得

z≡0(mod18)。

由于

35317|(3253-1)=34328124=22·35·35317,

故由(10)式可知,35317|36x17u(x-z)19v(x-z),但是由于35317是质数,所以35317|36x17u(x-z)19v(x-z)不成立。

所以(6)式没有整数解。

情形2x

36x=nz-x(325z-323yny-z)。

(11)

设n=2r3sn1,r+s≥0,gcd(n,6)=1,此时(11)式可化为

22x32x=2r(z-x)3s(z-x)n1z-x·

(325z-323y2r(y-z)3s(y-z)n1y-z)，

(12)

由此可见n1=1，且有

325z-323y2r(y-z)3s(y-z)=22x-r(z-x)32x-s(z-x)。

(13)

情形2.1 若r=s=0,则由(13)式得

36x+323y=325z。

(14)

由引理3知，(14)式仅有解(x,y,z)=(2,2,2)与x

情形2.2 若r=0,s>0,则由(13)式得

x=s(z-x),且有

325z-4x=17y19y3s(y-z)。

(15)

对(15)式取模3，得1≡(-2)x(mod3),则2|x；

对(15)式取模17，得2z≡22x(mod17)；

对(15)式取模19,得2z≡22x(mod19)。

若z=2x,则可设x=2x1,z=4x1,

于是(15)式变为

(3252x1+4x1)(3252x1-4x1)=17y19y3s(y-z)。

(16)

因17|(3252x1+4x1),17|(3252x1-4x1),

19|(3252x1-4x1),

则323y|(3252x1-4x1),但

323y>3236x1=(3233)2x1>3252x1>3252x1-4x1。

所以(15)式没有整数解。

若z>2x,则2z-2x≡1mod(323)。

于是120|(z-2x)且x为偶数,则6|z。

设x=3x1,z=6z1,因此

(3252z1-22x1)(3254z1+24x1+3252z122x1)=

17y19y3s(y-z)。

(17)

若17|(3252z1-22x1),

则17y|(3252z1-22x1),

但17y>17z>11z=116z1=(1331)2z1>3252z1-22x1不可能。

若17|(3254z1+24x1+3252z122x1),

即17|(54z1+5x1+4x1+z1)不成立。

所以(15)式没有整数解。

若x

于是120|(3x-z)且x为偶数,则6|z,这与z>2x情形一样。

所以(15)式没有整数解。

情形2.3 若r>0,s=0,则由(13)式得

x=s(z-x),且有

(325z-3x)2r(z-y)=17y19y。

(18)

显然r(z-y)≠0,则(18)式左为偶数,右为奇数,矛盾。

所以(15)式没有整数解。

情形2.4 若r>0,s>0,则由(13)式得

3x=r(z-x),x=s(z-x),且有

(325z-1)2r(z-y)=17y19y3x(y-z)。

(19)

显然r(z-y)≠0,则(19)式左为偶数,右为奇数，矛盾。

所以(15)式没有整数解。

综上所述,对任意的正整数n,Diophantine方程

(36n)x+(323n)y=(325n)z

仅有正整数解(x,y,z)=(2,2,2)。