天然气压气站管道异常振动及减振措施研究*

刘恩斌，廉殿鹏，苏中亚，谢 萍，尚 臣，陈其锟

(1.西南石油大学 石油与天然气工程学院，四川 成都 610500；2.中国石化中原石油工程设计有限公司，河南 郑州 450006；3.国家管网西部管道公司，新疆 乌鲁木齐 830000；4.卡迪夫大学 工程学院，英国 卡迪夫 CF24 3AA)

0 引言

管道振动是天然气输送过程中常见的1种破坏形式，严重地威胁着管道安全[1]。强烈的管道振动不仅容易产生噪声污染，严重损害作业区员工的身心健康；还会造成管道、管件及站场设备的连接部位松动，引发输送介质泄漏[2]。

针对管道振动问题，众多学者从基础理论和实验等多方面进行研究。Kadri等[3]研究管道气流脉动对水平管道气液流动段塞长度和频率的影响；周斌[4]对比分析有无基础振动对管道动态特性的影响；蓝天等[5]通过对二氧化碳往复式压缩机管道振动原因分析，降低管道振动对设备的危害；闫家鹏[6]计算压力不均匀度，并证明其理论可以很好地用于指导实践活动；宋微等[7]计算对比干、湿模态下悬跨管道的振动情况，分析影响水下管道自振频率的因素及其发生涡激振动的响应规律；Khudayarov等[8]采用具有弱奇异遗传核的Boltzmann-Volterra积分模型描述管道应变过程，提出求解黏弹性管道流体流动的一维振动和稳定性问题的算法[9]；侯慧敏等[10]分析压力管道水流流态对管道振动的激励特征并提出优化设计方案；Wu等[11]采用流体与结构数据交换的流动结构补偿方法，研究管道结构与内部气流相互作用下的管道自激振动问题。本文运用Caesar Ⅱ与Fluent软件相结合的方式，对某压气站进行管道振动分析与治理，对管道的正常运行具有指导意义。

1 数值计算基本理论

1.1 控制方程

湍流模型选用Realizablek-ε模型，其优点是可以保持雷诺应力与真实湍流一致，与实际流动的物理情况相符[12]，同时用管道轴向控制方程描述其结构行为。

1.2 流体流动模型

1.2.1 质量守恒方程

质量守恒方程如式(1)所示：

(1)

式中：x，y，z分别为三维坐标方向；vx，vy，vz分别为速度在x，y和z方向的分量，m/s。

1.2.2 动量守恒方程

动量守恒方程如式(2)所示：

(2)

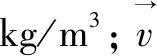
2 管道建模及模型验证

2.1 Pro/E模型

运用Pro/E软件对涉及三通和弯头较多的振动管段进行建模，同时为加快计算速度，对模型进行必要的简化处理，最终建模效果及进出口如图1所示。

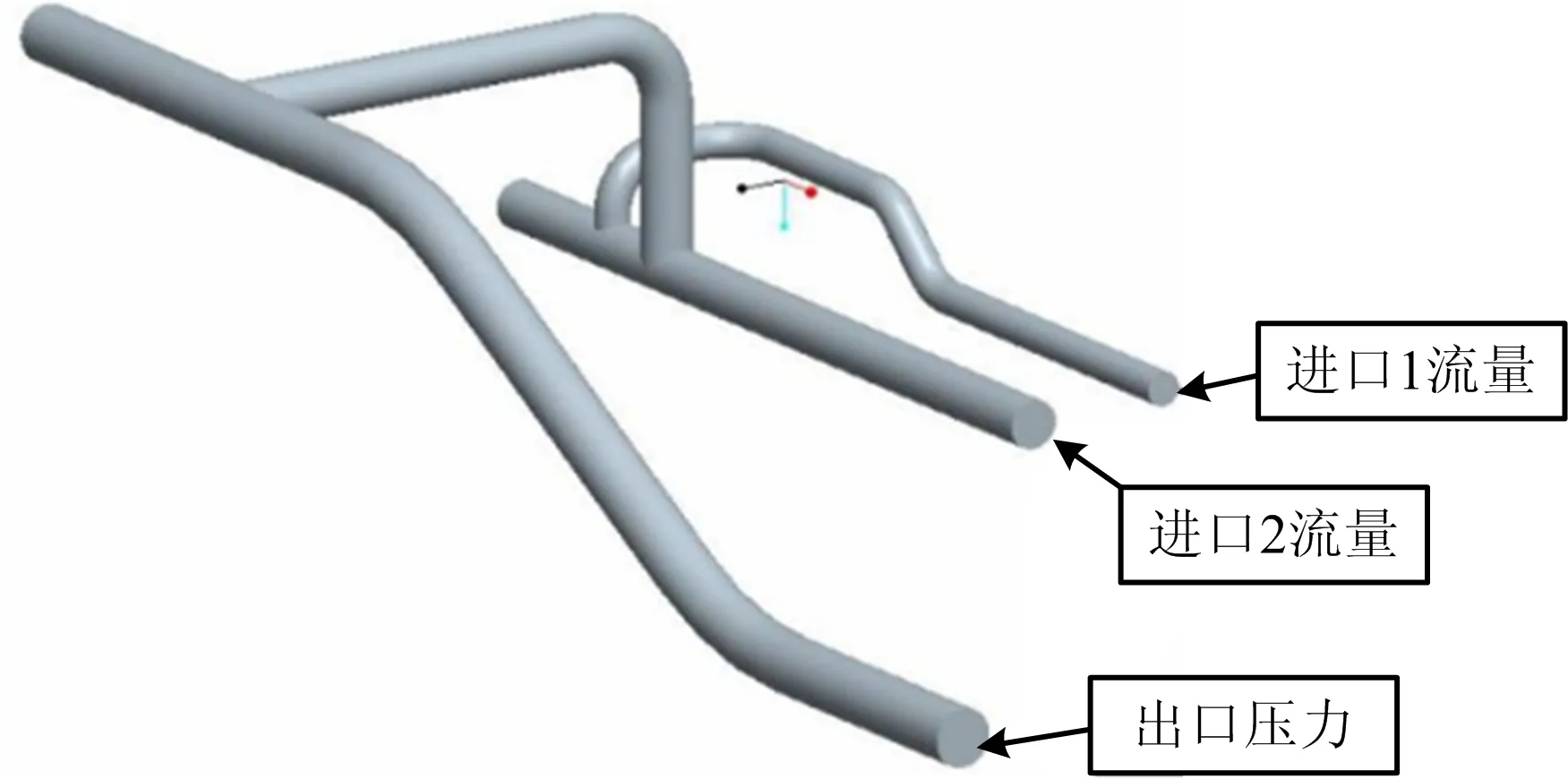
图1 Pro/E简化模型Fig.1 Pro/E simplified model

将Pro/E建立的模型导入ICEM中，对振动区域进行网格划分，其网格局部放大图及网格质量如图2所示。网格质量均大于0.35，在壁面附近具有良好的边界层，网格疏密程度适中，能够很好地满足后续计算要求。

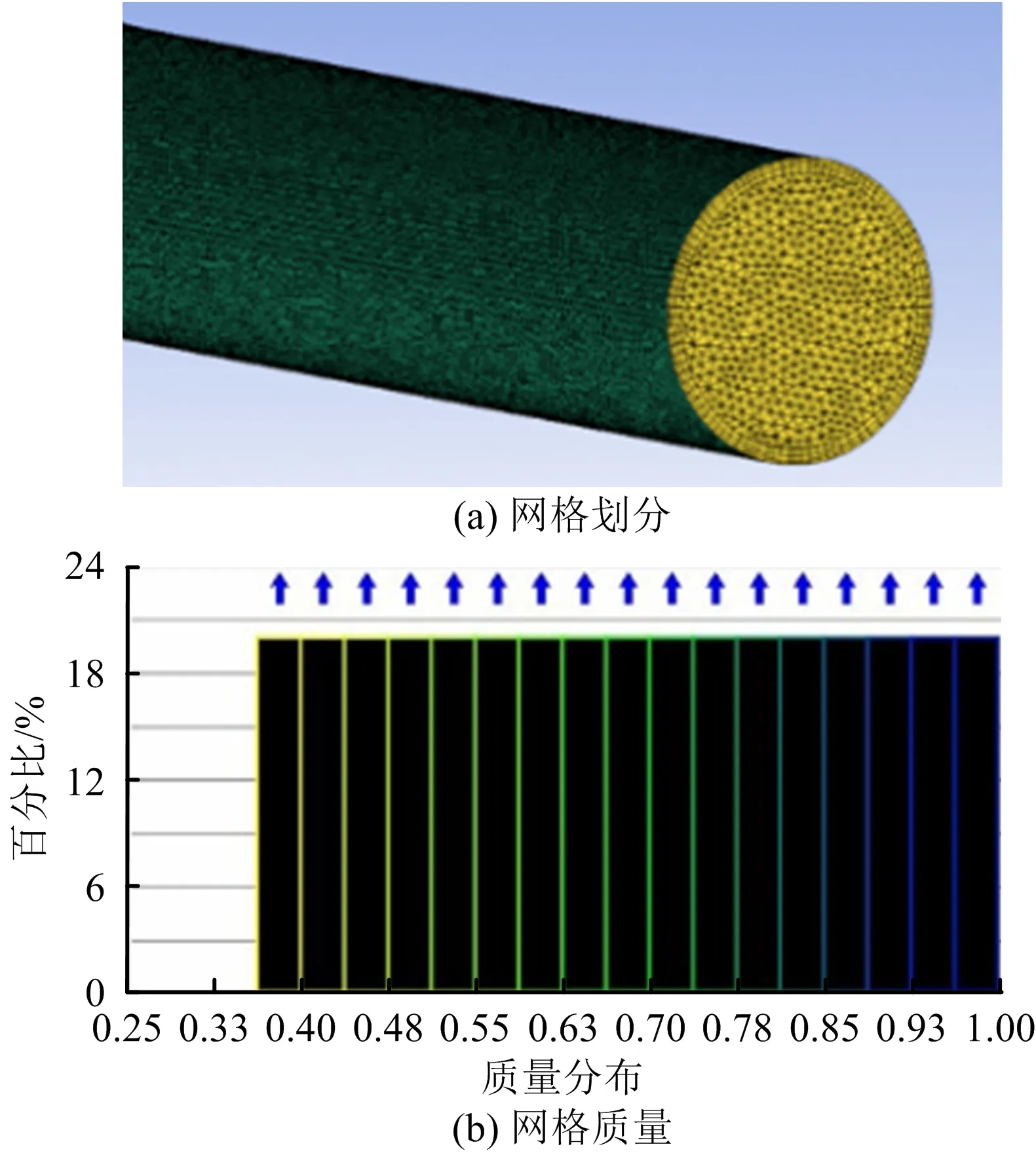
图2 管道振动模型局部网格及网格质量Fig.2 Local grid and grid quality of pipeline vibration model

2.2 现场测试分析

管道建模后进行初步流致振动分析，确定现场检测时的13个振动监测点，并取测量时间内的最大振动速度，如图3所示。按照ISO10816国际振动标准中的相关规定，对振动测试结果进行评价。

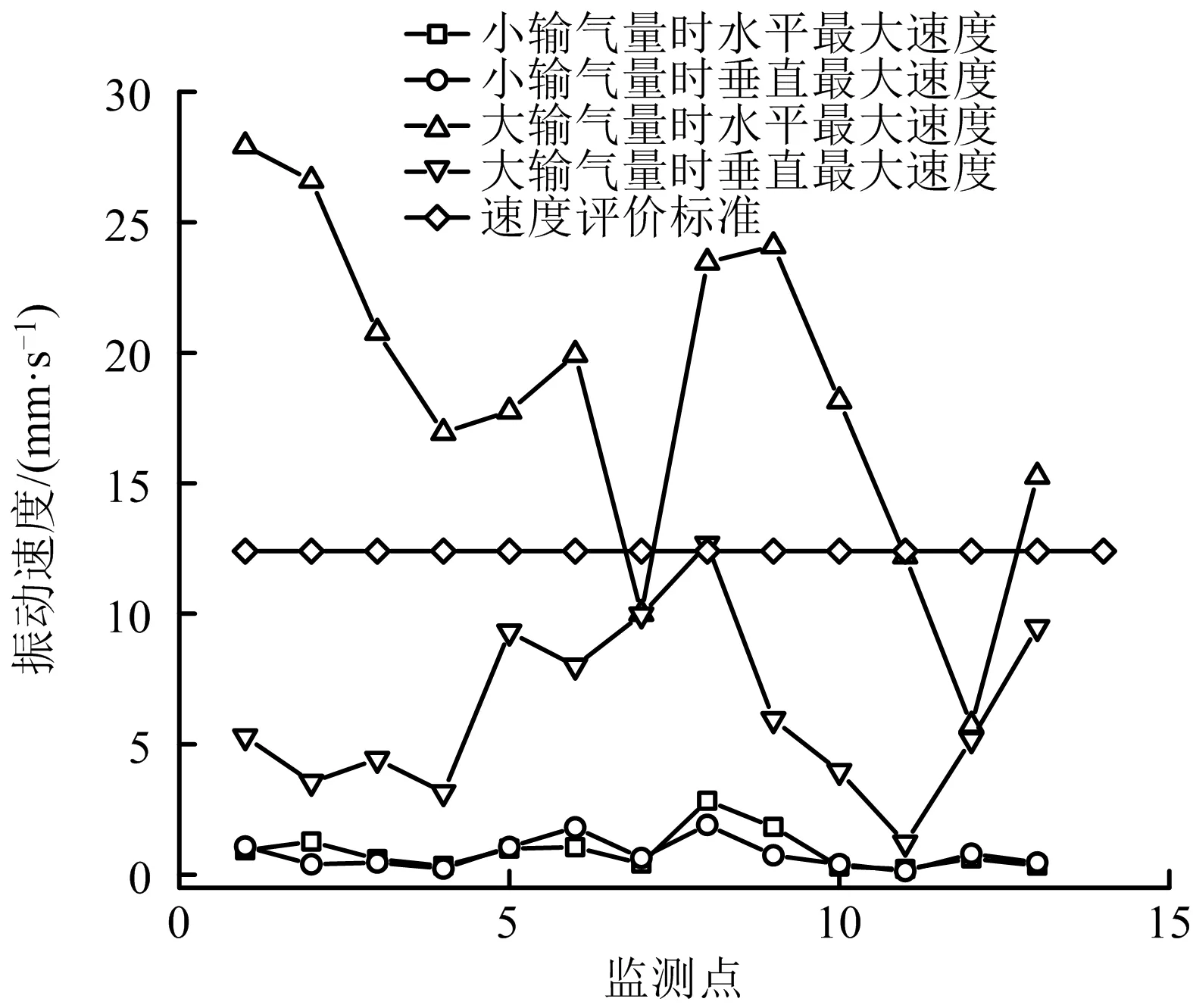
图3 振动测试点的振动水平评价Fig.3 Vibration level evaluation of vibration test points

由图3可知，当输气量小时，监测点振动速度均在优秀范围，无需进行管道振动治理，当输气量大时，其振动速度较大，需要对管道进行振动治理，由此可得管道异常振动与站场输气量密切相关。

2.3 模型验证

将现场测量结果与流致振动分析结果进行比较，不断调整流致振动分析模型。在进行数值模拟时，以测试条件下的工况为模拟工况，比较模拟工况和实际测量时的管道节点最大振动速度，验证流致振动分析模型的准确性。

以测试工况进口1流量：5 000×104Nm3/d，进口2流量：4 000×104Nm3/d，通过建模分析其流场，并进行曲线拟合得到各监测点的最大振动速度，通过对比，以达到验证模型准确性的目的，对比结果如图4所示。

图4 竖直最大速度对比Fig.4 Comparison of vertical maximum velocity

整体来看，在测试工况和模拟工况条件下，管道各主要节点的最大振动速度数值比较接近，在误差控制范围之内，说明流致振动分析模型符合现场实际情况，分析结果可信。

3 内部流场及流致振动分析

3.1 多工况管道内部流场分析

根据其工艺运行特点，得知压气站发球筒管道振动与管径为Φ711 mm的西二线、西三线联通管线密切相关。因此，在进行流场分析时，根据其运行方式不同，设计3种极端工况，通过这3种工况之间的交叉比较，可以验证联通管线对管道振动的影响，找到管道振动的原因，数值模拟的3种工况条件如表1所示。

表1 数值模拟工况Table 1 Numerical simulation condition table

3.2 各工况下流场模拟结果

由分析得，整个发球筒管内压力过渡比较平缓，但在弯头和三通区域，压力会出现明显变化。同时天然气在联通管内的流速较高，特别是在部分弯头处，因此监测点位置应重点放在弯头和三通区域。

3.2.1 涡核图

在Fluent流场分析过程中，对管道涡流核心区域设置压力波动监测点。3种工况下涡核图及压力监测点位置如图5所示。

图5 各工况涡核图Fig.5 Vortex core diagram under various working conditions

从涡核图中可以很直观地看出管道形成涡流比较剧烈的区域，其中涡核主要集中在弯头、三通部分，涡核图有助于在涡流核心区域更准确地设置监测点，分析其压力波动。

3.2.2 波动频谱图

整合各监测点的流体压力波动，对其进行FFT变换，3种工况下管道涡流核心区域压力波动的频谱图如图6所示。

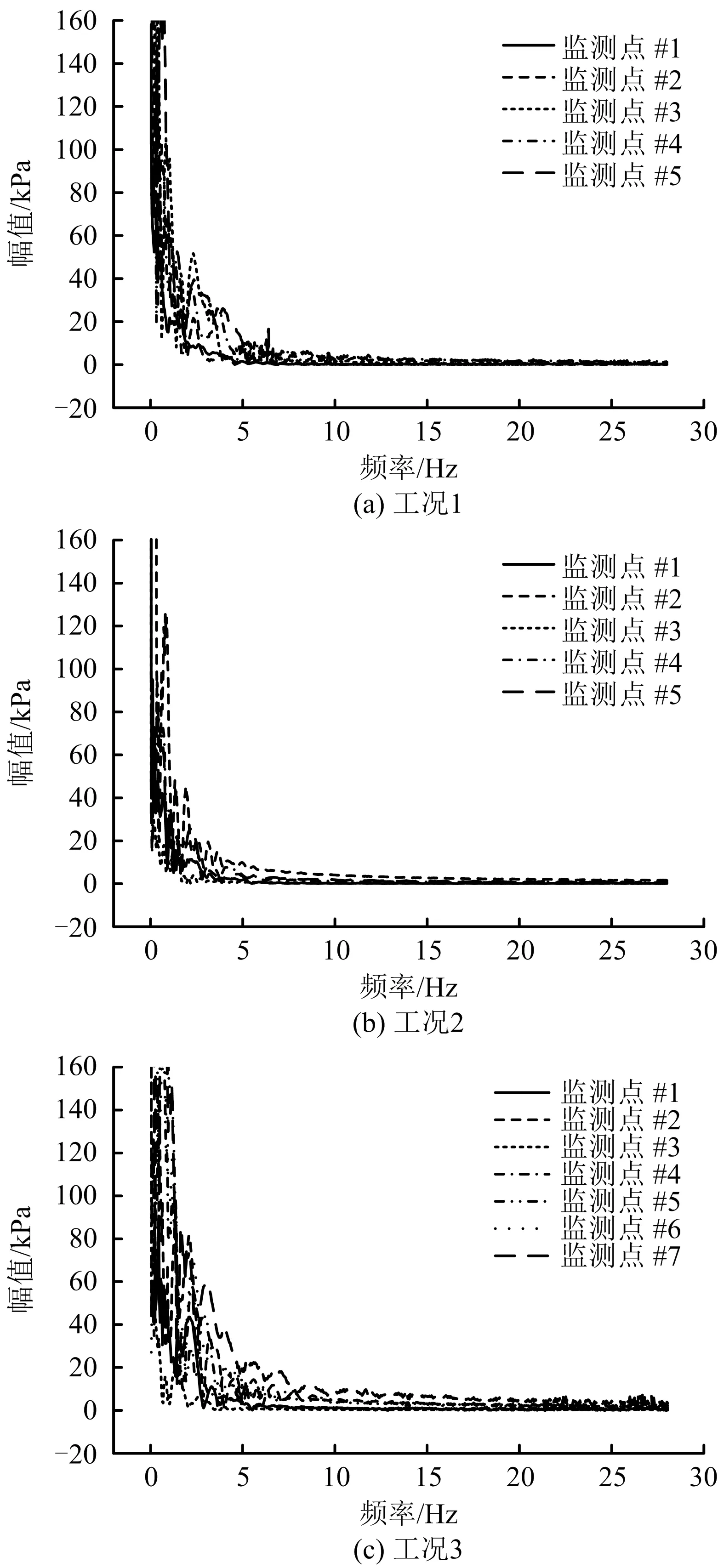
图6 各工况频谱图Fig.6 Frequency spectrum diagram under various working conditions

通过3种工况下管道内涡流核心区域压力波动频谱的分析发现，管道内压力波动的频率主要集中在低频范围内(0～7 Hz)。如果管道系统的固有频率与管道内压力波动的频率接近，那么管道系统就容易发生共振现象。因此，需要对管道系统的固有频率进行分析。

3.3 管道流致振动分析

3.3.1 管道系统固有频率分析

为判断管道系统是否发生共振，利用Caesar Ⅱ软件对振动管段进行固有频率分析[13]，前20阶固有频率如图7所示，第1阶固有频率下的振型如图8所示。

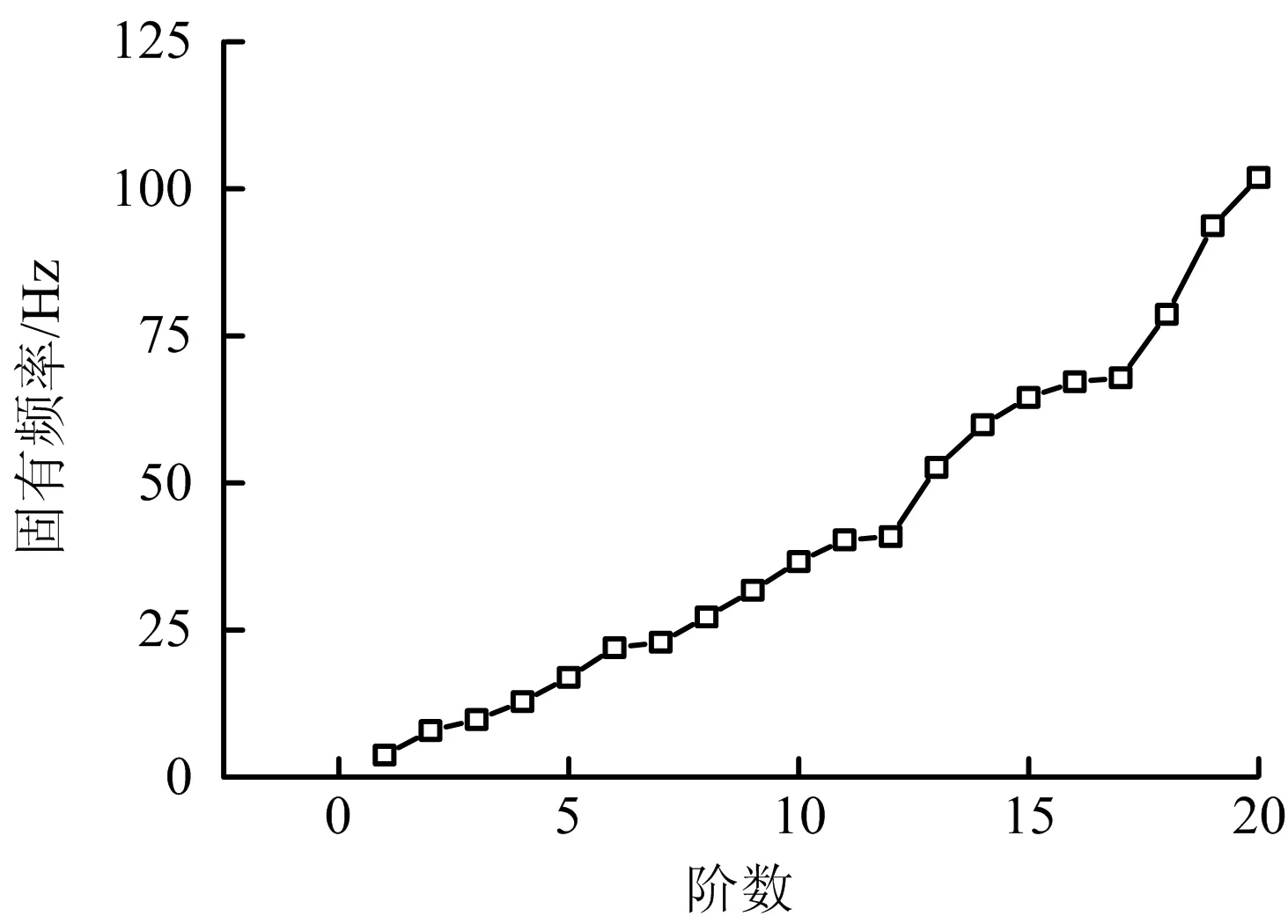
图7 振动管段固有频率Fig.7 Natural frequencies of vibration pipe section

图8 第1阶固有频率下的振型Fig.8 Vibration mode at first order natural frequency

由图8可知，在第1阶固有频率为3.755 Hz时，管道在4 500节点以及4 800节点附近有较大的水平方向振动趋势。通过管道内部的流场分析发现，管道内压力波动频率与管道系统的前2阶固有频率接近，因此，管道容易发生共振现象，使振动变得更加剧烈。

3.3.2 管道振动位移、速度分析

在流场模拟及固有频率分析的基础上，将流场模拟所得的管道激振力施加到相应的弯头和三通位置，利用Caesar Ⅱ软件对某压气站的振动管段进行振动位移和振动速度的分析[14]。分别定义每组力的大小、方向、作用位置以及其他控制参数，得到3种工况下的最大振动位移，并通过数值拟合，得到各主要节点水平方向的最大振动速度，如图9所示。

图9 各工况下主要节点水平方向最大振动速度Fig.9 Maximum horizontal vibration velocity of main nodes under various working conditions

通过3种工况下的最大振动位移和最大振动速度分析发现：1)管道振动主要集中在水平方向，在管道轴向和竖直方向基本不存在振动现象；2)管道振动最剧烈的位置位于发球筒管道的盲板附近以及平衡管线附近，其他位置的振动均较小；3)管道异常振动与管道内的压力波动有关，由于二、三线的联通管线经过弯头和三通后，与三线出站前管线相连，流体在联通管内的流速高，进入到出站前汇管后，流体流速突然变低。因此，在该处的三通附近形成强烈的涡流波动，进而产生流体激振力，引起管道的振动。

4 管道减振措施

压气站的管道振动由管内流体激振力导致，对其振动治理应主要从2方面入手，即增加管道支撑和改变配管方案：通过设置锚固墩和管夹约束，提高管道系统的刚度，使其能够抵抗流体激振力；通过增大联通管线的管径，改变流体的流动状态，减小流体激振力[15]。

根据上述原则，提出3种整改方案。方案1：在管道上设置锚固墩和管夹约束；方案2：改变联通管线的走向和管径(由Φ711 mm改为Φ1 016 mm)，以减小弯头个数，同时按方案1的方式增加锚固墩及管夹约束；方案3：改变联通管线的走向和管径(由Φ711 mm改为Φ1 016 mm)，不增加锚固墩和管夹约束。整改治理方案的示意如图10所示。

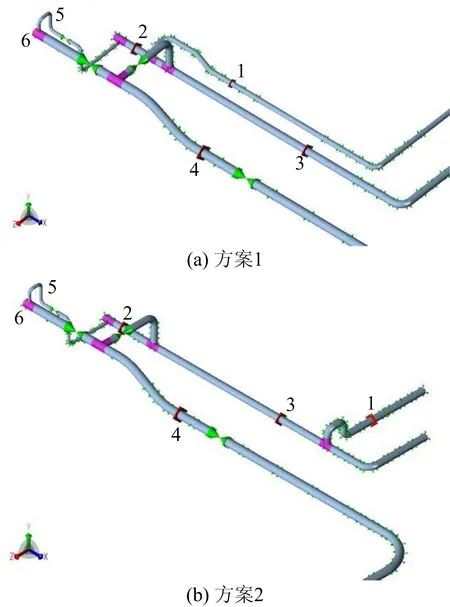
图10 整改方案示意Fig.10 Schematic diagram of rectification scheme

在图10中，1，2，3，4为所添加的锚固墩，5为平衡管线处的管夹约束，6为盲板处的斜拉弹簧约束。

4.1 整改后管道固有频率分析

以管道流致振动分析时的工况3为例，分析各整改方案的减振效果。利用Caesar Ⅱ软件对整改后管系振动管段进行固有频率分析发现，改管后压力同样在低频范围内波动，但由于改管后，管系的固有频率提高，其第1阶固有频率变大，与压力波动的频率相差较大，因此，管系中不会存在共振现象。

4.2 整改后管道位移、速度分析

运用Caesar Ⅱ软件分析整改后各管线振动情况，求得其水平方向的最大振动速度如图11所示，并运用上述同样方法，分析各整改方案的减振效果，计算各方案的理论减振效率。

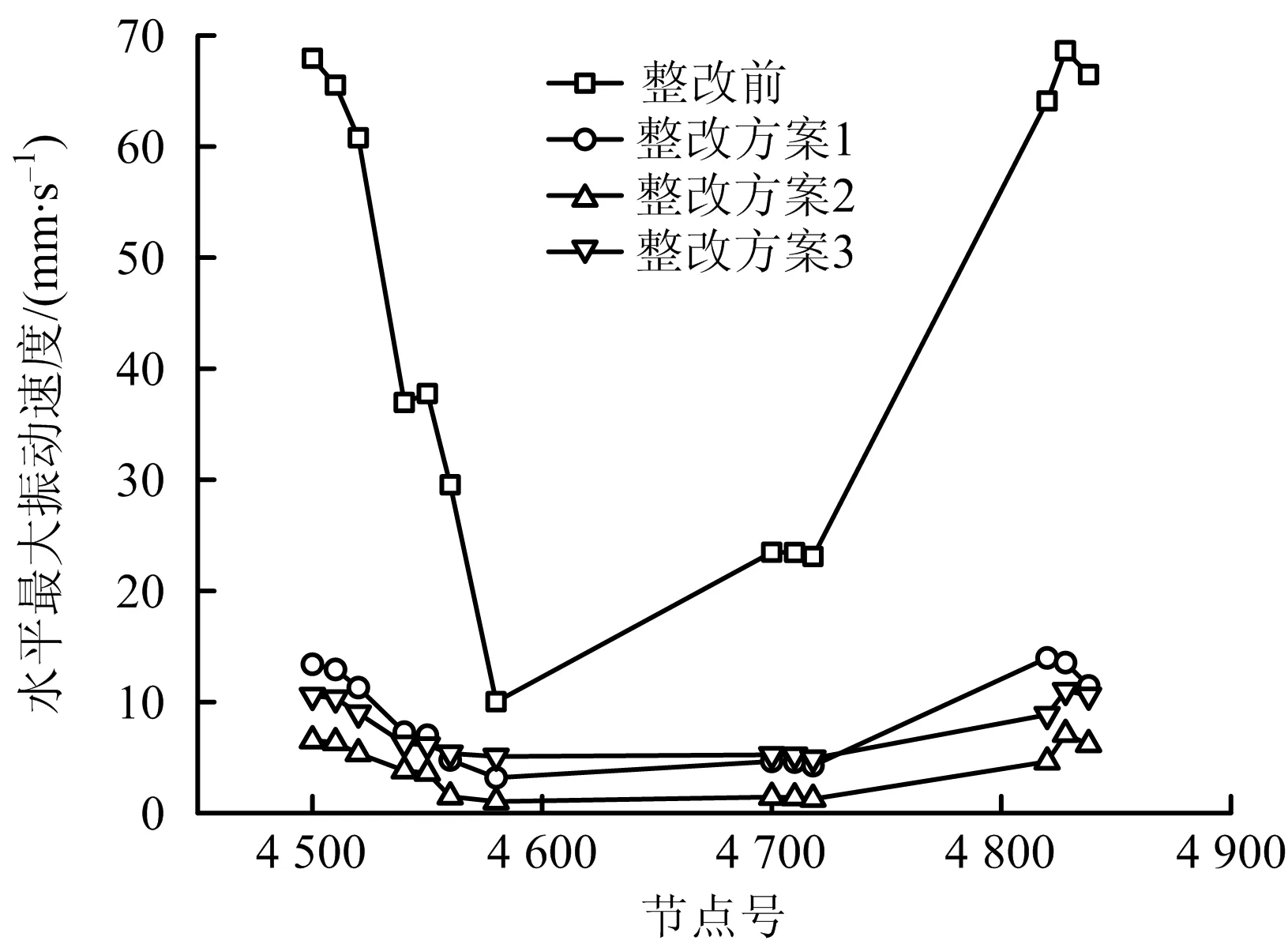
图11 治理前后最大振动速度对比Fig.11 Comparison of maximum vibration velocity before and after treatment

由图11可以看出，3种整改治理方案均能达到比较好的减振效果，整改方案1的理论减振率可达到68%～83%，整改方案2的理论减振率可达到90%～95%，整改方案3的理论减振率可达到78%～86%(在统计理论减振率过程中，原本优秀的数据，不计算在内)。

5 结论

1)管道内的流体压力波动是导致管道出现异常振动现象的主要原因，压力波动产生随时间变化的流体激振力，这些激振力作用在弯头、变径管等处，引起管道的异常振动现象。

2)通过管道内流体压力波动频谱的分析，发现管道内压力波动主要集中在低频范围内(0～7 Hz)，通过Caesar Ⅱ软件发现，管道系统的第1阶固有频率为3.755 Hz，第2阶固有频率为7.906 Hz，管道内压力波动频率与管道系统的前2阶固有频率接近，因此，管道系统发生共振现象，使振动变得更加剧烈。

3)在管道减振中，优化管道结构和增设锚固墩相结合的方法可以达到最好的减振效果，其理论减振率达到90%以上。