非线性退化椭圆型方程弱解的存在唯一性

陈方敏， 严 畅， 柴晓娟

(安徽大学数学科学学院， 安徽 合肥230601)

1 引言

带低正则值的椭圆方程广泛产生于流体力学、控制问题以及海洋和大气科学的湍流问题中，引起了学者们广泛的关注[1-3]. 在[1]中，G.Stampacchia 最早证明了外力项为Radon 测度的线性椭圆方程解的存在唯一性， 即

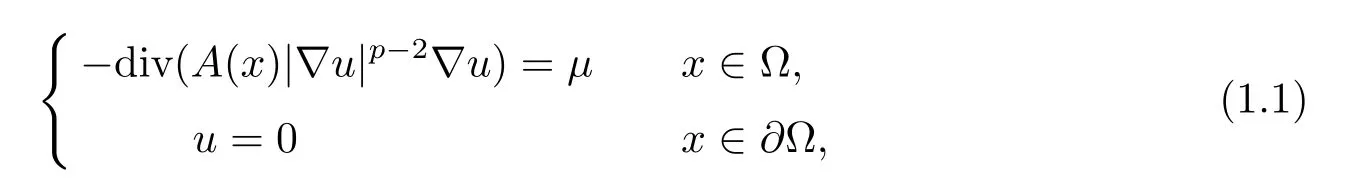
其中A(x) 满足一致椭圆假设， 即存在α ＞0， 使得对任意ξ ∈RN， 有

2 定理1.1 的证明

为了证明上述定理， 我们先给出几个引理.

引理2.1 假设Ω⊂RN为光滑有界区域，θ ＞0，q ＞1，g ∈L∞(Ω)， 那么

推论2.5 取引理2.3 中un和u， 那么∇un在Ω 中几乎处处收敛到∇u，∇u的定义如注2.3 所述.

即u满足(1.7).

3 定理1.3 的证明

且当f ≤g在Ω 中几乎处处成立， 可得u ≤z在Ω 中几乎处处成立.

证 由(1.9)-(3.2)， 可得

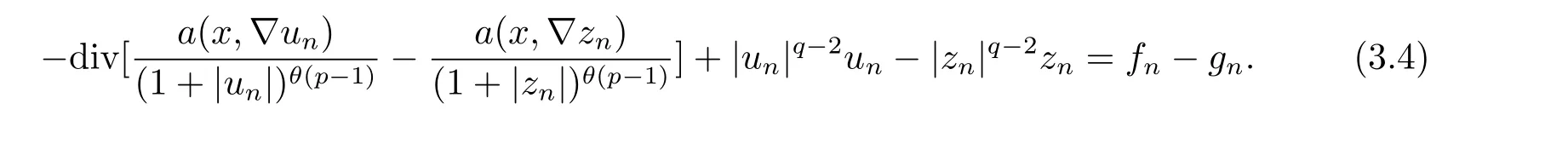
即问题(1.3)的逼近解是唯一的. 证毕.