荷载工况多目标下钢筋混凝土深梁的拓扑拉压杆模型设计

张鹄志，黄垚森，郭原草，徐文韬

(1.湖南科技大学土木工程学院，湖南 湘潭 411201；2.湖南科技大学结构抗风与振动控制湖南省重点实验室，湖南 湘潭 411201)

在钢筋混凝土(简称RC)深梁构件配筋设计问题上，GB 50010—2010 《混凝土结构设计规范》(2015版)建议的基于试验数据的半经验设计方法存在配筋结果较保守、力学理论支撑不足等缺点；而其他国家的规范，如美国[1]，则有拉压杆模型等应力设计方法的建议。研究表明，渐进演化类算法等拓扑优化方法是构建拉压杆模型的一种可靠且有效的思路[2-5]，但这类方法大多基于某特定的单一荷载工况目标开展优化，无法满足工程结构设计中考虑自重荷载、人群荷载、风雪荷载、地震荷载等多种复杂荷载工况的需求。因此，研究多荷载工况目标下的钢筋混凝土深梁等复杂受力构件优化设计方法很有必要。

结构拓扑优化算法中工程应用较多的有两类，一类是渐进结构优化类算法，源自Xie等[6]在1993年提出的渐进结构优化(简称ESO)。该算法基于应力分布进行迭代优化，逐步删除结构中的低效或无效单元，演化出结构拓扑。这类算法之后又根据不同的演化方向和淘汰机制衍生出递增结构优化[7]、双向结构优化[8]、遗传演化结构优化[9](简称GESO)等，特别是GESO，引入概率性淘汰机制，抑制了ESO棋盘格现象等缺陷并提高了这类算法的全局寻优能力。另一类是Bendsoe等[10]提出的固体各向同性材料惩罚模型(简称SIMP)。SIMP模型具有程序设计简单、便于实现和工程应用等优点，但灰度单元等问题仍需进一步解决。以上这些拓扑优化算法在机电设计[11]、汽车制造[12]、建筑结构[13]、工程力学[14]等领域都得到了一定的应用，但运行中均缺乏能考虑多种荷载工况的运用方式。有学者针对该问题展开研究，特别是关于荷载工况多目标下的病态荷载问题，如秦浩星等[15]将应变能目标函数归一化，获取最优工况权重系数，提出多工况结构拓扑折中规划模型；杨德庆等[16]利用映射变换解法处理荷载工况多目标下的病态荷载问题。这些研究在一定程度上推动了多目标拓扑优化算法的发展，但在工程应用，特别是在土木工程领域，还面临较多的困难。因此，解决荷载工况多目标下的病态荷载问题，借助拓扑优化算法构建拉压杆模型，分析模型并据之探讨构件受力特性，以期形成深梁类构件的拓扑拉压杆模型设计方法。

1 荷载工况多目标GESO及拉压杆模型

1.1 荷载工况病态的处理

在有限元建模分析中，面临多荷载工况(P1，P2，…，Pn)时，如果某荷载值Pi远大于另一荷载值Pj，可能造成模型中部分单元在这两个工况下的应变能或应力灵敏度存在数量级的差别，从而导致较小荷载工况对最后的拓扑解无法体现，即出现荷载工况多目标下的病态荷载。

1.2 荷载工况多目标GESO

荷载工况多目标GESO中，对第k个工况下单元应变能表达式[9]如下：

(1)

式中：Ci,k、Ti、ui——在第k个工况下第i个单元的应变能、刚度矩阵与位移向量。

此时，荷载工况多目标下单元应变能灵敏度如下：

Ci=max{Ci,1,Ci,2,…,Ci,k,…,Ci,n}

(2)

(3)

式中：Vi——第i个单元的体积(面积)；l——存活单元总数。

由于优化对象材料的密度是均匀的，因此物体的质量与体积(面积)呈线性关系，可在优化过程中定义性能指标T[9]：

(4)

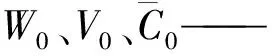
利用式(1)和式(2)实现以给定质量下刚度最大为目标的优化，利用式(4)逐代记录的T值完成最优拓扑的判定。

荷载工况多目标GESO的具体步骤如下：(a)建立钢筋混凝土有限元模型，给出约束条件与荷载等价化处理后的荷载条件；(b)分别求解结构在每种荷载工况下的平衡方程，获取单元相应的应变能灵敏度；(c)提取每个单元在各荷载工况单独作用下的应变能灵敏度最大值，作为其在该代的灵敏度；(d)判定是否满足停止准则，若满足，则跳出循环；否则继续优化；(e)选择所有存活单元进行杂交与变异等遗传算子操作；(f)根据优化准则完成选择与舍去，返回步骤(b)。

荷载工况多目标GESO的流程图如图1所示。

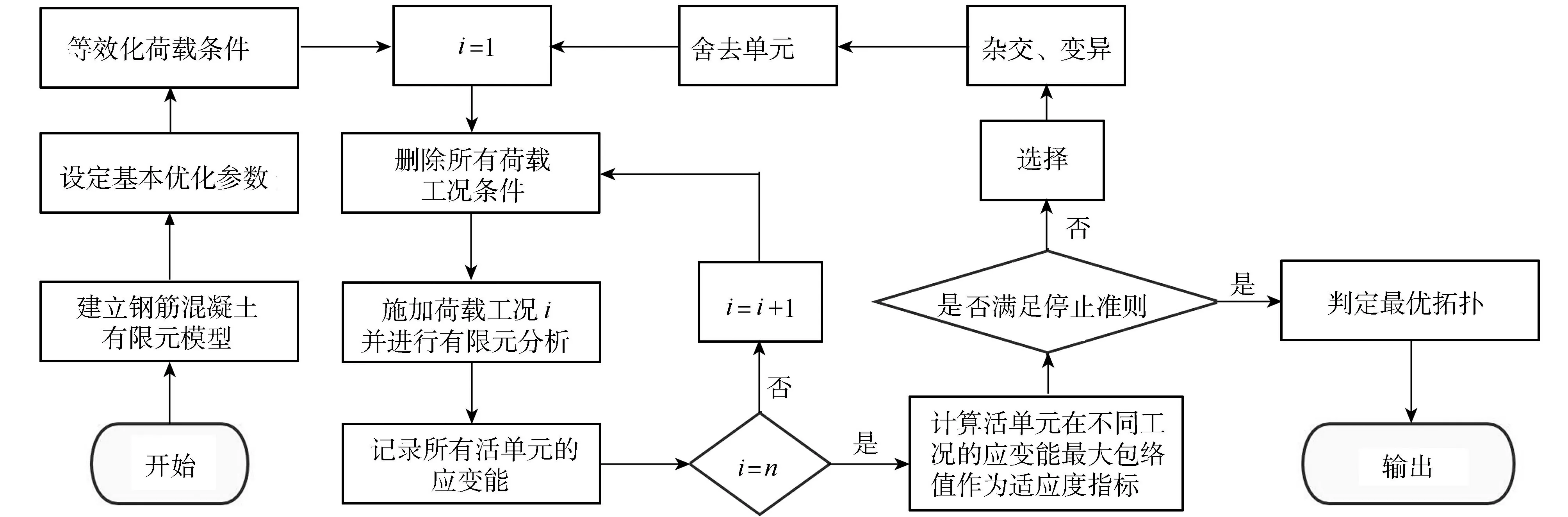
图1 荷载工况多目标GESO的流程Fig.1 Flow chart of multi-objective GESO of loads

1.3 拓扑拉压杆模型的力学计算

在将荷载工况多目标GESO的拓扑解用于辅助拉压杆模型以指导配筋设计时，需先求解拉压杆模型的轴力分布，该轴力分布为各个荷载目标下的拉压杆模型的轴力包络值分布。

2 钢筋混凝土深梁算例

2.1 单侧开洞简支深梁

单侧开洞简支深梁，梁宽b=160 mm，其余尺寸如图2(a)所示。第一个荷载工况为单独承受向下的P1=100 kN，第二个荷载工况为单独承受向下的P2=100 kN。利用ANSYS中的APDL二次开发平台来实现荷载多目标GESO，利用善于处理平面应力问题的八节点单元——plane82平面单元建立钢筋混凝土整体模型，以实常数表达梁宽信息。在该模型中，钢筋混凝土被作为一种兼具良好拉压性能的复合材料来模拟，泊松比取0.2，弹性模量取28 GPa，单元尺寸为20 mm×20 mm，基于线弹性分析结果进行优化。此外，参考文献[9]的研究结论，变异率和杂交率均取0.2，最优个体选择率取0.3。

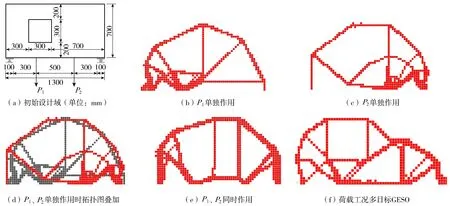
图2 单侧开洞简支深梁的拓扑优化Fig.2 Topological optimization of simply supported deep beam with a one-side opening

算例在各种不同荷载工况目标下的拓扑解如图2(b)～(f)所示。从图2(b)(c)(e)可知，单一荷载工况下的拓扑解演化为较清晰的杆系结构，是易于参照构建拉压杆模型的；而直接叠加两个荷载工况的拓扑解得到的图2(d)，是较为混沌的，据之建立拉压杆模型较为困难。根据荷载工况多目标GESO的具体步骤与流程图完成荷载工况多目标GESO，得到的图2(f)正是兼顾两个荷载工况目标完成GESO所得的拓扑解，已显示为典型的杆系结构。从图2(f)可以看出其与前面几种拓扑解的显著区别，至少说明荷载工况多目标GESO，与按单目标优化分别获取不同荷载工况下的拓扑解，再弹性叠加这些拓扑解的优化方式，以及与按同时作用多种荷载工况的单目标优化相比，优化路径完全不同。参照图2(f)人工完成拉压杆模型的建立，再展开两个荷载工况分别单独作用下的拉压杆模型结构力学分析，杆件内力结果及其包络结果见图3(图中数字表示受拉时的包络限值，括号内的数字表示受压时的包络限值)。在建立拉压杆模型时，为了使构建的拉压杆模型更贴近拓扑解，参考文献[17]的观点，拉压杆模型并非桁架模型，在保证计算弯矩较小时，可以将这些拉压杆模型中杆件间的连接均采用刚结点。由于在P1单独作用下杆件AB弯矩最大，MAB=0.63 kN·m；在P2单独作用下杆件CD弯矩最大，MCD=0.39 kN·m。可见，不管作用哪个荷载工况，模型中的弯矩水平均相当低，可以忽略不计。假定所有杆件的抗弯刚度EI均相等时，正应力可以忽略不计，利用该拓扑解能够建立以P1、P2为荷载工况目标较理想的拉压杆模型。同时，由该模型能够较好地满足所设计荷载工况的受力性能表明：先等价化荷载后，再在构建拉压杆模型时考虑实际荷载工况条件这一思路可以避免荷载病态现象。

图3 荷载多目标GESO所建拓扑拉压杆模型的轴力解及包络结果(单位：kN)Fig.3 Axial force solutions and their envelope results of topological Strut-and-Tie model constructed by multi-objective GESO of loads (unit: kN)

为了进行对比，根据图2(b)建立拉压杆模型，同样完成两个荷载工况分别单独作用下的拉压杆模型结构力学分析(所有杆件抗压刚度EA均取等值)，杆件内力结果见图4。虽然图4(a)和图4(b)分别与图3(a)和图3(b)中的轴力水平相差不大，但图4(a)中杆件EF的E端和杆件GI的H端弯矩值已达到一定的数量级，如此高的弯矩水平显然不符合拉压杆模型特性，该拉压杆模型无法满足另一个荷载工况目标，是不合理的。

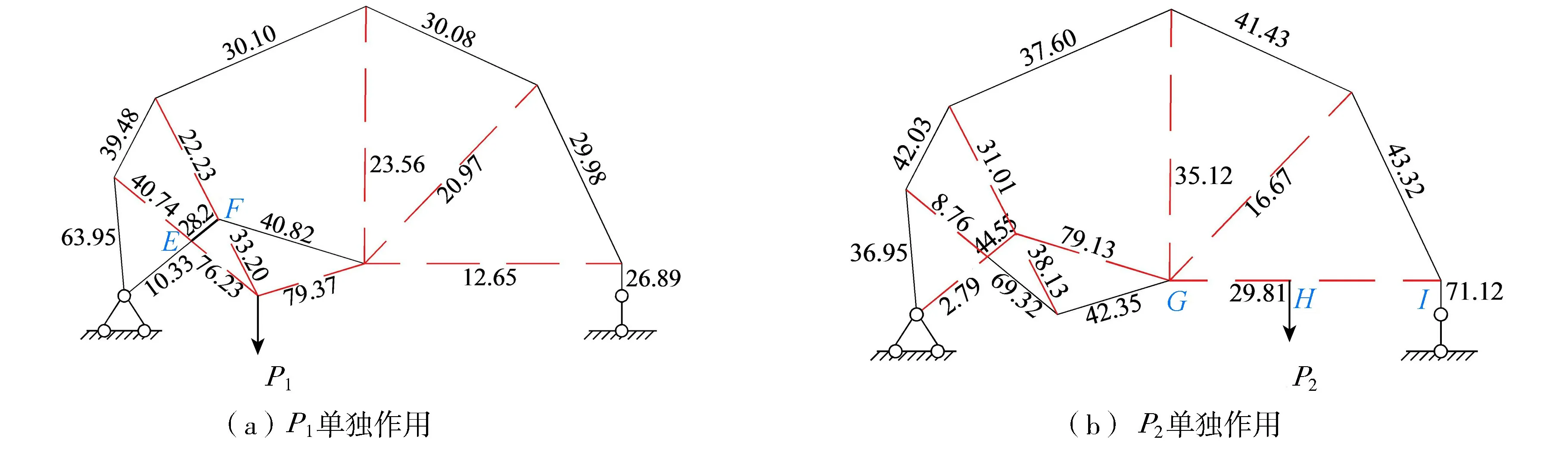
图4 P1工况对应荷载工况单目标GESO所建拓扑拉压杆模型的轴力解(单位：kN)Fig.4 Axial force solutions of topological Strut-and-Tie model constructed by single-objective GESO of load case P1 (unit: kN)

再根据图2(e)建立拉压杆模型，完成两个荷载工况分别单独作用和共同作用下的拉压杆模型结构力学分析，杆件内力结果及两个荷载工况单独作用的轴力包络结果见图5(图中数字表示受拉时的包络限值，括号内的数字表示受压时的包络限值)。

a.在P1单独作用下杆件JK弯矩最大，MJK=4.07 kN·m，在P2单独作用下杆件LM弯矩最大，MLM=2.62 kN·m，表明仅从弯矩水平来看，不管是P1还是P2单独作用，该P1与P2同时作用作为单独工况对应的荷载工况单目标GESO所建立的拓扑拉压杆模型都劣于荷载工况多目标GESO所建立的拓扑拉压杆模型。

b.比较图3(c)和图5(c)的应变能水平，假定两种拉压杆模型中的杆件轴向刚度均为定值抗压刚度，按下式计算每根杆件的应变能和模型的平均应变能：

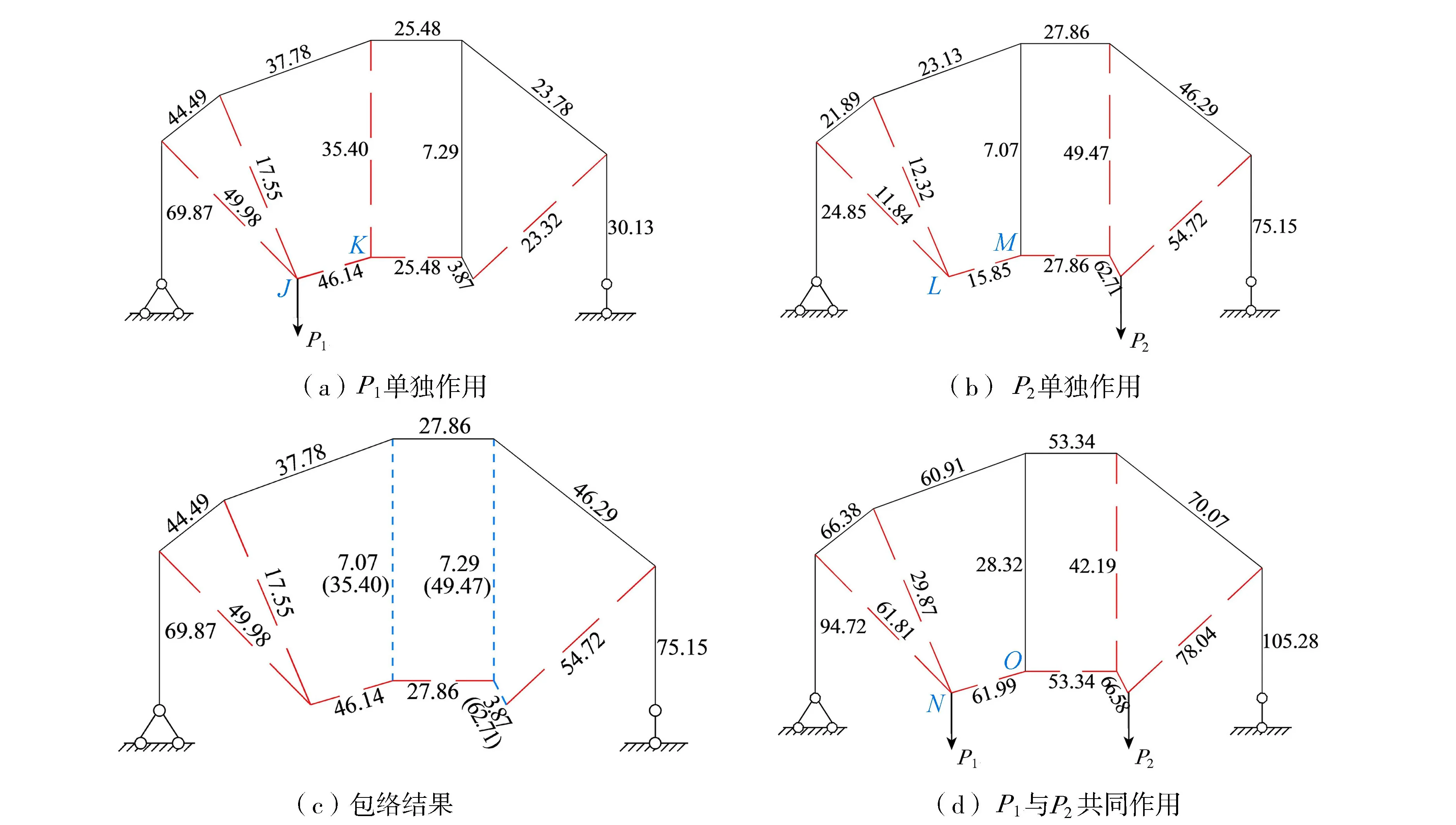
图5 P1与P2共同作用工况对应荷载工况单目标GESO所建拓扑拉压杆模型的轴力解及包络结果(单位：kN)Fig.5 Axial force solutions and their envelope results of topological Strut-and-Tie model constructed by single-objective GESO of applying load cases P1 and P2 simultaneously(unit:kN)

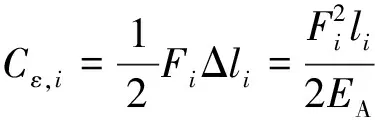
(5)

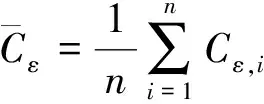
(6)

c.在P1与P2共同作用下杆件NO弯矩最大，MNO=1.37 kN·m，但从图5(d)可以看出，模型的轴力水平已远远高于图3(c)。所谓荷载工况多目标，即这些荷载工况一般不会同时作用(同时作用的实际是荷载单工况目标问题)，所以如果直接参照图5(d)进行配筋设计，明显是极不经济的，此时，荷载工况多目标下拉压杆模型设计方法的价值就更加突显。

2.2 3种荷载工况加载时两端固定铰支深梁

3种荷载工况目标下的两端固定铰支深梁，梁宽b=160 mm，其余尺寸见图6(a)。3种荷载工况分别为单独承受向下的P1=100 kN、P2=100 kN和P3=100 kN。荷载工况多目标GESO所得的拓扑解如图6(b)所示。

图6 3种荷载工况加载时的简支深梁荷载工况多目标GESO拓扑优化Fig.6 Topology optimization of simply supported deep beam loaded by three points by multi-objective GESO of loads

图7所示的拓扑解出现了少量不对称的细节，这是由于GESO中引入了遗传算法，优化过程具有概率性所引起的，此外，计算浮点误差时也可能造成这种现象。从传力路径的角度上看，杆件的主要传力路径集中在几根主斜压杆上，这些主斜压杆均对称；其余为次要传力路径支杆，不对称的情况也主要发生在这些支杆上。出于简化，以图6(b)的右侧部分为主要参考，参照图6(b)建立如图7(a)所示的拉压杆模型。在完成结构力学分析(所有杆件EA均取等值)时，发现这些支杆的内力水平远低于主要杆件，基本可以忽略。进一步简化忽略支杆，建立精简后的拉压杆模型，如图7(b)所示，并得到轴力包络结果。经计算，该拉压杆模型结点弯矩很小，可以忽略。从图7(b)可以看出，该拉压杆模型下，内力水平和分布均较合理，传力3种荷载工况下的传力路径均明确且简洁，证明了荷载工况多目标GESO的稳定性及面临更多荷载工况目标时的优化能力。

图7 3点加载简支深梁的拓扑拉压杆模型Fig.7 Topological Strut-and-Tie models of simply supported deep beam loaded by three points

在以上荷载工况多目标GESO算法和拓扑拉压杆模型建立方式下，一方面，不同边界条件下的深梁所得到的拉压杆模型轴力解结果均未出现对某一荷载工况作用的忽略，即有效避免了荷载病态现象，说明等价化荷载后再构建拉压杆模型时，考虑实际荷载工况条件这一思路是可行的；另一方面，由于GESO对棋盘格现象良好的抑制能力，依据其拓扑解建立拉压杆模型是一条直观可行的思路。

2.3 钢筋混凝土深梁的配筋建议

由文献[4]深梁的配筋设计试验结果可知拉压杆模型设计的深梁，一方面能保证承载力，另一方面能节省钢筋用量，同时更加符合深梁的复杂受力特性。此外，由于GB 50010—2010《混凝土结构设计规范》(2015版)践行极限状态设计法，认为受拉混凝土在开裂后退出工作，荷载通过钢筋拉杆及未开裂混凝土构成的压杆进行传递[17]。结合本文算例，经荷载工况多目标GESO建立的拓扑拉压杆模型及其结构力学分析结果，给出如图8所示的配筋建议方案，其中图3(c)和图7(b)的拉压杆结果可分别参考图8(a)和图8(b)进行配筋设计。

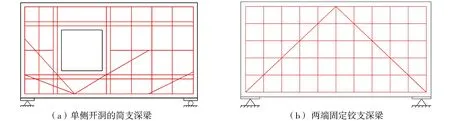
图8 钢筋混凝土深梁的钢筋布置建议Fig.8 Reinforcement layout suggestions for RC deep beams

3 结 论

a.在荷载工况多目标优化设计时，先等价化荷载以求取拓扑解并据之建立拉压杆模型，再逐一输入每个实际荷载工况值完成力学分析，取杆件轴力包络值作为设计参考，可以有效解决病态荷载问题。

b.在GESO的每一代遗传演化前，每个单元取其在各工况单独作用下的应变能最大值作为该代灵敏度参数，GESO算法即被拓宽至可以处理荷载工况多目标优化问题。

c.根据拓扑解建立拉压杆模型并完成力学分析，以模型杆件内力水平及分布为指标进行比较，各种荷载工况单目标优化方式得到的拓扑解都劣于荷载工况多目标GESO，表明荷载工况多目标GESO的全局寻优能力较强。

d.荷载工况多目标GESO可以较有效地抑制棋盘格现象，获取较清晰的杆系结构拓扑解，依据其建立拉压杆模型是一种直观可行的方法。