夯实概念意义 增进负数理解

江苏省盐城市阜宁县实验小学 邱桂华 苏志妹

负数是小学数学系统知识的一部分。学生在学习了整数、分数、小数之后，再认识负数，可以运用类比的方法去学习负数的相关知识。但是，在练习中发现学生对负数知识的掌握依然不牢固，尤其是有关负数位置的确定方法。经过研究，发现学生对负数概念在现实生活中的实际意义掌握不牢，脱离了生活实例去应用负数知识、练习负数习题。笔者重新审视教材，深入了解学生的学习困难，从负数的概念意义、负数之间的大小关系和数直线上负数的顺序定位三个角度，去分析问题的原因，探究解决问题的策略。

一、问题凝视

练习中，学生在完成如下图所示的题目时，总是出现错误，找不准-11、-4 的位置。无论是在数直线上，还是在数轴上，对于相关负数的对应位置都不能快速、准确地定位。

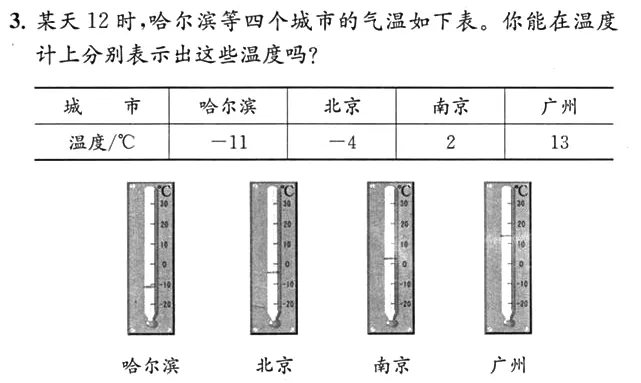
二、成因透视

为什么有些学生不能快速找到相关负数的对应位置？为什么有些学生在经过长时间思考后，还是找不对相关负数的对应位置？为什么有些学生在解答有关负数位置的题目后，出现反复修改的现象？经过调查，总体来看，有些学生找不准相关负数的对应位置的原因是学生对负数概念的实际意义缺少透彻的认识，对负数之间的大小关系缺乏明确的认知，对负数在数直线上的顺序定位理解不够清晰。

1.负数概念意义理解不透彻

负数是小学阶段学生所认识的数系统中一类数的概念，是数大家庭中的一种分类，与整数、分数和小数组成一个数的体系。负数概念的感知、建立方法与整数、分数和小数概念建立的方法是相通的。教学此节课时，需要教师利用类比教学方法和生活实例感知方法引导学生对这类知识进行建构。

2.对负数之间的大小关系认知不明确

负数之间位置的对应与负数之间的大小关系有一定联系，有些学生存在-11>-10、-5>-4 等错误认知，导致找不对相关负数的对应位置。

3.数直线上负数的顺序定位理解不清晰

数直线是很直观的小学数学工具，能够帮助学生清晰地找准数的位置、明确数之间的大小关系和相应的前后顺序。学生在学习整数、分数、小数时，都会借助数直线来深化对数概念的理解和数系统的建构。在学生借助数直线学习负数时，受到整数在数直线上顺序定位的影响，会出现学习的负迁移，往往把相邻的负数位置弄颠倒，以至于出现错误，如-5 与-6 在数直线上的位置。

三、出路审视

研究北师大版数学教材四年级上册和人教版数学教材六年级下册负数的教学内容，再结合苏教版数学教材五年级上册有关负数的教学内容，发现教材都是先让学生对负数有丰富的现实生活材料的感知，明确负数在现实生活中的实际意义，然后再引入0 这个数字，结合正数，把负数融入数系统之中，深化学生关于数系统的知识结构，最后结合数直线，运用数形结合的教学思想和教学方法，加深学生对负数的认知，形成完整的知识结构，按照规律明确数直线上负数的顺序位置。

首先，让学生充分感知有关负数知识的生活实例，列举大量的生活中具有相反意义的量，如温度的零上与零下、方向的高低、金钱支出与收入等，让学生形成丰富的感性认识。然后引入数字0，由0 与某个具体正数的关系，来类比推导0 与某个具体负数的关系，由此明确0 到负数的距离，加深学生对负数概念的理解，利用0 到某个具体负数的距离找准负数的位置。

其次，在充分感知负数的生活实际意义的基础上，借助某个生活实例，让学生初步认识负数的大小关系。如借助温度的实例，先让学生从生活实例出发，明确零下6 摄氏度比零下1 摄氏度气温低，在温度计上，零下6 摄氏度在零下1 摄氏度之下，让学生初步认识-6 与-1的大小关系，意识到负号后面的数字越大，这个负数越小，越在气温计的下面。学习负数的大小关系是一个从具体到抽象，再从抽象到具体的过程，即从具体到抽象的过程是认识负数大小关系的过程，而从抽象到具体的过程是运用负数大小关系解决生活问题的过程，以此来找准负数的位置。另外，教师也得考虑小学中高年级学生思维的抽象水平。

最后，借助数直线，运用数形结合的思想和方法，使学生形成完整的数系统知识结构。在数直线上，让学生先找出0 的位置，分清楚正数和负数在数直线上的方位，然后让学生完善或填写数直线的正数部分，再运用迁移的学习方法，特别强调相反的方向，按照相同的数字排列规律，完善或填写数直线的负数部分，以此找准负数的位置。

四、片段重构

在图表上确定相关负数位置，如-6、-4、-9、-11等，先让学生独自去完成，出现错误也不要紧，要给学生试错的机会，可以运用负数的数学历史知识，让学生知道，即使是历史上伟大的数学家也对负数的价值存在错误的认知。然后让不同的学生讲解这个题目，从负数概念的实际意义、负数之间的大小关系和数直线上负数的顺序定位角度解答此类题目。

片段如下：

做练习时，学生在温度计上标注-11 的位置时出现错误，把-11 标注在-10 之上。

教师指出错误，展示数学历史知识，让学生树立信心，细心听取同学的解答。

教师展示：

负数历史小知识

当负数已经在东方出现了两千多年时，在西方，尽管负数的运算法则在16 世纪就已经产生，但它仍然得不到数学家们的认可。1544 年，意大利数学家卡尔达诺在《大术》中承认方程有负根，但又认为是不可能解的，负数是“假数”，只有正数才是“真数”；法国数学家京韦达、笛卡尔也不承认负数，把它叫作“不合理的数”。17 世纪，帕斯卡同样也对负数持怀疑态度，并认为用0 减去4 纯粹是胡说。到19 世纪，英国数学家仍然不用负数，在他们看来，负数是荒谬的。克菜因说，从演绎数学诞生开始，数学家花了1000 年才得到负数概念，又花了 1000 年才接受负数的概念。

学生1：老师，我会解答，可以利用0 到-11 的距离来解决这个题目，0 到-11 的距离是11，而0 到-10的距离是10，因此，-11 应该标注在-10 之下，只有这样，-11 到0 的距离才会大于-10 到0 的距离。

学生2：我有不同的方法，用负数之间的大小关系来确定-11 的位置，零下11 摄氏度气温更冷，-11 小于-10，所以，-11 的位置应该比-10 的位置低。

学生3：老师，我还有不同的做法。可以联系数直线，这个温度计相当于把数直线竖立起来，在数直线上，-11的位置在-10 的左边，所以，在温度计上，-11 的位置应该比-10 的位置低，而-10 的位置应该比-11 的位置高。

教师：以上三位同学从不同的角度解答了这个问题，思路也都十分清晰，同学们更喜欢哪种方法呢？无论同学们选择哪种方法，一定要知道，负数是来源于我们的生活，一定要结合现实生活实例去理解负数。另外，负数是对正数的补充，是与正数相反的，在理解负数时，一定要联想正数的相关知识，只有这样，才能把负数学好。