让策略学习成为学生解决问题的习惯

余兰芝 郭运动

《义务教育数学课程标准（2011年版）》在课程总目标中指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力。”解决问题的能力是学生数学素养的重要体现，培养学生良好的解决问题的习惯能够让学生更好地解决实际问题。在进行解决问题的教学时，老师应选择合适的实际问题，使学生经历解决实际问题的过程，鼓励学生理解分析、探寻解决问题的思路和方法，综合运用已有知识经验解决问题。下面以苏教版四年级下册第五单元“解决问题的策略”教学为例，加以论述。

一、抓关键词句，通过变式练习培养审题习惯

学生在解决问题时，认真读题、审题是正确解题的关键。在平时的课堂教学中，老师要有意识地培养学生读题、审题的习惯，经常通过一些变式练习，帮助学生养成找题目中的重点词句并能准确理解的习惯。

比如，在本单元教学中有这样一道练习题：“把正方形的边长增加4厘米，得到一个大正方形，面积比原来增加72平方厘米，原来正方形的面积是多少平方厘米？”学生在练习时，往往会因为对“边长增加4厘米”理解不到位而做出错误的解答。针对此问题，我在此题之后又出示以下几道题，让学生通过对比，认识到正确审题、理解“边长增加4厘米”的重要性。

补充题1：把正方形的一组对边各增加4厘米，面积就比原来增加72平方厘米，原来正方形的面积是多少平方厘米？

补充题2：一个边长20米的正方形荷花池周围有一条宽1米的小路。小路的面积是多少平方米？

通过比较，学生发现：同样是“边增加4厘米”这个条件，原题是将正方形的边长增加4厘米，增加后还是一个正方形，而补充题1是将正方形的一组对边各增加4厘米，增加后就形成了一个长方形。这两道题条件不同，增加部分虽然都是“72平方厘米”，但是这“72平方厘米”的形状也是不一样的，最后的解答过程和结果当然也就不一样。而原题与补充题2相比较，增加后都形成了一个正方形，但原题中正方形的边长只是增加了4厘米，而补充题2中正方形的边长却增加了2个1米。

对题目当中的条件做适当改变的题组练习，可以增强学生对题意的辨析和理解。除此之外，看清问题要求的是什么，也是正确解决问题的关键。于是，我又增加了补充题3：把正方形的边长增加4厘米，得到一个大正方形，面积比原来增加72平方厘米，现在正方形的面积是多少平方厘米？将原题当中的问题求“原来”正方形的面积改成了求“现在”正方形的面积。往往学生在单独解答此类题目时，不注意问题是求“原来”还是求“现在”，通过组题对比的形式让学生练习，虽然只是简单地将“原来”改成“现在”，但就是这细小的改变，却让学生注意到看题目中的关键词句，养成细心看题的习惯。

二、数形结合，培养自觉画图整理思维的习惯

本单元教学的重点，是让学生学会用画图的方法整理条件和问题，借助直观图分析数量关系，寻求解题思路。很多问题都可以用画图的方法直观、简洁地表达出题意，将条件和问题之间的联系形象、生动地呈现出来。画图作为解决问题最常见的策略之一，应当成为学生的一种习惯。

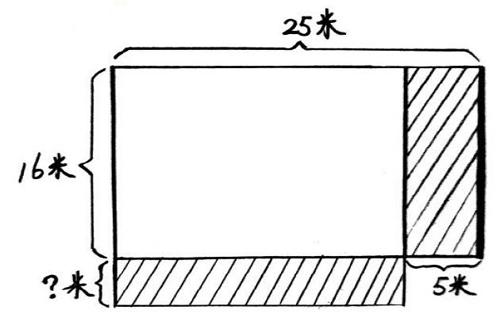
比如，本单元教学中有一道习题：“王叔叔家有一个长方形花圃，长25米，宽16米。因为要建新房，需要将花圃的长缩短5米。如果不改变花圃的面积，王叔叔要将花圃的宽增加多少米？”这道题如果只是凭空想象，可能会有一定的困难，但是如果动笔画一画图，就能很快清楚题目当中的数量关系（如下图）。

通过画图，学生很快发现：“长缩短5米”减少的部分是一个“长16米、宽5米的长方形”;“宽增加？米”增加部分的面积正好与这个“长16米、宽5米的长方形”的面积相等。其实，画出图后，求“宽增加？米”的问题就已经迎刃而解了。

从此类解题实际练习中，学生体会到画图策略的学习价值，自然产生愿意学习和应用画图策略的心理倾向，从而养成运用画图帮助分析整理难解的问题、化抽象为直观、化难为易的思维习惯。

三、多种解答，培养多角度思考与检验习惯

《义务教育数学课程标准（2011年版）》在课程总目标中的“问题解决”方面进一步提出：“（使学生）体验解决问题方法的多样性，发展创新意识。”在平时的教学中，老师应鼓励学生在解决问题时，从多角度思考和分析问题，经常有意识地引导学生想一想：“还有没有不同的解题思路？”“还可以怎样做？”学生就会逐渐养成从不同角度思考问题、大胆创新的良好习惯。在平时的练习中，老师一般都会提醒学生做完题目之后检查，最常用到的是“重复计算”“把得数代入原题”进行检验，以及“用另一种方法解答”等检验方法。所以，鼓励学生用不同方法解答，不仅可以培养学生多角度思考问题的习惯，同时也可以提醒学生“用另一种方法解答”进行检验，进一步培养学生自觉检验的良好习惯。

比如，本单元练习中有一道典型的和差问题：“两个小队的少先队员去植树，一共植了34棵。其中第二小队比第一小队多植4棵。两個小队各植树多少棵？”学生通过画线段图发现，解答这道题有两种明显的思路：一种是从总棵数里面减去4棵，就得到2个第一小队的植树棵数，先求出的是第一小队的植树棵数;另一种是将总棵数加上4棵，得到的是2个第二小队的植树棵数，先求出的是第二小队的植树棵数。学生不管选择哪种思路解决问题，老师都可以提醒学生先选择其中一种方法解答，另一种方法可以在自备本上算一算，看看两种方法所得的结果是否一样，从而检验自己做得对不对。

当学生用一种方法解答一道题后，进行再思考，可以提升学生思维的灵活性。有很多学生平时做完题不喜欢检查，但是其中有相当一部分学生却很愿意用另一种方法再算一算，因为这种方法不是机械重复，也不会那么枯燥。当然，在解决问题时，并不是所有的题都可以用另一种方法解答，但是，这种检验方法应深植学生心中，使学生的创新意识、多角度思考问题的习惯得到培养，良好的检查习惯也在潜移默化中逐渐形成。