声流理论及其传热传质研究现状与展望

杨延锋，姜根山，于 淼，姜 羽，刘月超

（1.华北电力大学 能源动力与机械工程学院，北京 102206；2.华北电力大学 数理学院，北京 102206）

广义地说，声流是有限振幅声波在黏性流体中传播时产生的与时间无关的稳流现象，或物体做自激振荡诱导的定常流现象。声流现象要么发生在自由非均匀声场中，要么发生在浸没于声场中的各种障碍物附近或振荡体附近。因此，声流现象在流体力学中被称为“steady streaming”，即定常流动；而在声学领域则被称之为“acoustic streaming”，即声流。

早在1831年，Faraday[1]首次观察到振荡膜上的稳态涡旋流动。之后，Rayleigh[2]对柱形空腔内由驻波引起的声流现象进行了理论分析，并给出了解析解。基于Faraday的实验观测和Rayleigh的理论模型，之后涌现了许多关于声流的论文，既有理论的，也有实验的。声波作用下，这种扰动物体边界层的流动对加速输运过程，如热源的热传递、清洁受污染表面、振动燃烧中液滴的雾化等具有十分显著的效果，且物体边界层内外的声流不仅能减小边界层的厚度，而且能促进边界层内的湍流[3]。因此，物体边界层内、外的声流受到了广泛关注和研究。

产生声流的两个必要因素[4]。①声波在自由空间传播时被吸收和散射而衰减:这种衰减在短距离传播中是微不足道的，但高强度声波的传播会导致足够大的压力衰减，从而产生稳定的整体流动，这类声流通常与高黏度的介质有关。②声波引起的振荡流与固体之间的摩擦损耗:这类声流只要存在一个振荡的切向相对速度即可产生，而相对运动的来源是来自流体中的声波振荡还是固体本身的振动并不重要。与空间衰减产生的声流不同，第②种情况诱导的声流包括两部分:内部流和外部流。Stokes边界层内的摩擦耗散产生了内流，而内部流又在边界层外诱导出尺度较大的稳定流，且这种边界层内、外的稳流现象总是呈反向旋转的涡流特性。此外，声流的速度随声强的增加而增加，但即使在目前可用的最高声强度下，声流速度仍小于介质的波动速度。

根据声流涡尺度大小，可将声流大致分为三类[5]:①Schlichting流。这类声流发生在物体黏性边界层中，且边界层中涡的尺度通常由黏性边界层厚度（δ=决定，其尺寸远小于波长，属于微尺度声流。②Rayleigh流。这类声流发生在物体边界层外，其涡尺度比Schlichting流涡尺度大得多，且边界层外漩涡的尺度与声波波长相当。③Eckart流。这类声流发生在自由非均匀声场中，声场的不均匀尺度远大于声波波长，其旋涡尺度也远大于声波的波长，该类流动与Schlichting流和Rayleigh流不同，是一种大尺度现象。理论研究表明，对于以上三种声流，黏性力是驱动稳定涡流的必要条件。然而，从某种程度上说，以上三种按声流尺度的分类是不科学的。因为在实验条件下，不同类型的声流可以同时发生；其次，不同类型的声流可以具有相同的依赖性，如对流体介质黏度和声场参数的依赖性。目前，国外期刊文献中有各类声流的研究文章，如Zarembo（1971）对声流理论和实验工作进行了合理详尽的调查，但之后对声流研究现状再无相关综述类文章。相比之下，国内还没有对声流问题进行系统的梳理，因此，本文的工作将对国内声流问题的研究和发展起到一定的指导性作用。

1 声流理论

1.1 声流控制方程

声流运动也属于流体运动。因此，声流运动同样受到Navier-Stokes动量方程和连续性方程控制[6]

式中:u为流速矢量；p为流体的压强；μB为体积黏滞系数；μ为切变黏滞系数。边界层内的声流主要受到切变黏滞系数μ的影响，而自由空间的声流主要受到体积黏滞系数μB的影响。

根据扰动理论展开法[7]，声波作用下考虑二阶流场信息的流场变量可表示为

式中:ε为一个小参量，满足ε＜＜1；变量的下标0、1、2分别为静态量、一阶量和二阶量。一阶速度、压力和密度是时间的谐波函数，由声波方程控制。而二阶量是非线性现象的体现，即声流。

将式（3） 代入式（1）、式（2） 并保留二阶量，则可得到声流的控制方程

因为声流是与时间无关的稳态流，因此分别对式（4）、式（5）取时间平均可得声流的控制方程

式中，＜＞为对物理量在整个振荡周期内取时间平均。由式（6）、式（7）可知，一阶场量是驱动二阶场量的源项。式（6）右边的一阶场量为驱动二阶场量的质量源；而式（7）右边的一阶场量为驱动二阶场量的体积力。

1.2 声流流函数方程

在较多的理论研究中为了更形象地研究声流的流场结构，常通过引入流函数ψ来研究物体外稳定声流的流场特征。根据二维笛卡尔坐标系、柱坐标和球坐标下不可压缩Navier-Stokes方程和连续性方程，经消除压力项p后，分别引入相应的流函数表达式（ψ1，ψ2，ψ3），可得到流场流函数微分方程[8-10]。

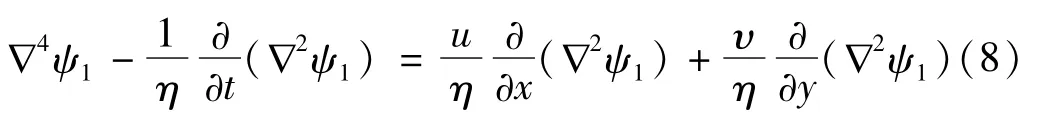
其中，

其中，

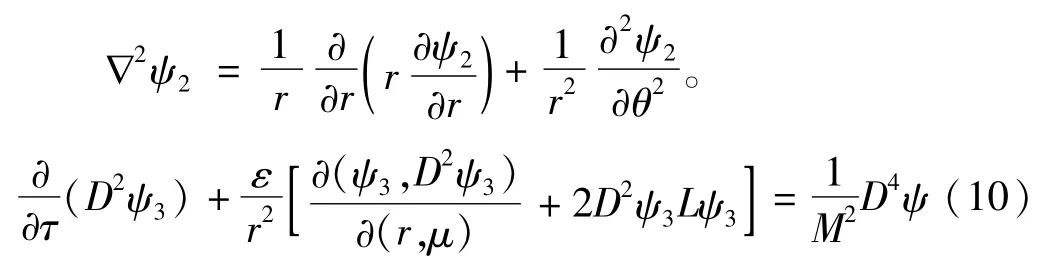
其中，

式中:r=r′/R；τ=ωt；ε=U0/ωR；M2=ωR2/η。经理论推导发现，流函数方程式（8）、式（9）、式（10） 的解包含两部分:一是与时间无关项，即声流；二是依赖于时间的振荡流。因此流函数方程可描述于两部分解之和，ψ=ψs+ψueiωt。且对于二维柱坐标和球坐标下的声流流函数方程总有特定形式的解:ψs=f（r）sin 2θ。

目前关于物体外声流理论的研究还局限在小振幅（ε＜＜1）范围，即声波引起的振荡流或物体做自激振动都属于小振幅振动。在小振幅（ε＜＜1）的极限条件下，已有学者实现了边界层内、外涡流流场的同时求解。

2 固体表面附近声流的流场结构研究

了解固体表面附近声流流场结构是进行物体与周围环境传热传质研究的基础。因此，对不同结构模型中声流流场结构的研究一直是许多学者探索的重点内容。目前，研究最多的结构模型包括:二维柱体和球体外的声流、二维矩形通道中的声流（如经典的Kundt’s Tubes模型）、同轴环柱间的声流以及二维椭球外的声流，包括相应的理论研究和声流流场可视化的实验研究（PIV（particle image velocimetry）技术）。 而对于三维声流结构的研究还鲜有报道。

研究表明，固体边界层内外的流动取决于固体特征尺度D、角频率ω、振荡振幅ζ0和介质运动黏度v。因此，学者们为方便讨论固体外的声流特征，定义了以下无量纲数

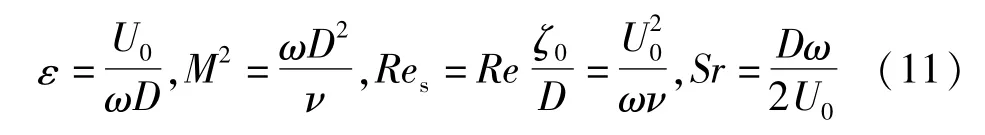
式中:U0为速度振幅；Re为传统的雷诺数，表征了惯性力和黏性力之比；Res为黏性边界层内、外涡流的尺度大小和强弱；斯特劳哈尔数Sr为非定常运动的强弱；ε为声波引起的振荡流位移振幅（ζ0=U0/ω）相对于模型特征尺度的大小，当ε＜＜1时，表明物体外的流场做小振幅波动；而当ε＞＞1时，固体外的流场将做有限振幅波动，具有强烈的非线性作用；M2为声波引起的黏性扩散深度与固体特征尺度D的相对大小，当M2＞＞1时，表明物体外的黏性边界层厚度，此时固体外具有极薄的黏性边界层。当Re数较小时，流体动量方程由Stokes方程控制；而当Re数足够大时，对流项的作用不可忽略，声流将由完整的N-S方程控制。

2.1 二维圆柱体外声流的流场结构

该问题的研究是针对圆柱体在静止的无界（或有界）黏性流体中做小振幅简谐振荡所引起的声流，即研究对象始终满足:ε＜＜1。固体在静止的黏性流体中进行小振幅、高频、周期性振动时，除了流动的预期波动成分外，还有一种时间无关的流动，即声流。

Schlichting[11]首次对圆柱体外的声流进行了研究，利用边界层理论方程逐级近似求解，得到该剪切波层外缘的二次定常流速分布。声流流函数研究表明，当圆柱作简谐振动时，在圆柱边界层外会产生四个与外缘相切的二次定常流动。Holtsmark等[12]对圆柱轴线垂直于不可压缩振荡流方向的二维流动进行了理论和实验研究，并与Schlichting理论解进行了对比，且理论解与实验结果符合良好。Holtsmark由一阶近似得到的第一象限内声流流动的流线图及实验图像，如图1所示。

图1 理论解及实验图像:圆柱体半径a=0.11 cm，外边界半径A=20aFig.1 Theoretical solution and experimental image:cylinder radius a=0.11 cm，outer boundary radius A=20a

Raney等[13]同样对圆柱在无限静止流体中做小振幅（ε＜＜1）自激振荡诱导的声流现象进行了理论分析和实验验证，并对Schlichting的理论解做了修正。Raney经严格推导给出了柱坐标下二维圆柱外部二阶声流流函数微分方程的显式解:ψ2=f（r）sin 2θ。Stuart[14]指出当圆柱作高流雷诺数Res小振幅振动时，Stokes层外的二次定常整流流动中惯性对流作用与黏性耗散作用相当，这时圆柱外表现为具有两层边界层性质的流动类型，即非定常Stokes剪切波层外的二阶定常整流流动也具有边界层性质，这一外层的流尺度与内部流尺度相比较大，但与圆柱的典型尺寸相比较小。Stuart的研究对后期传热分析奠定了基础。Riley[15]讨论了非定常黏性流体中物体振动引起的流动问题。并利用匹配渐近展开技术，建立了一个符合逻辑的自洽理论，并对满足ε＜＜1条件下，任意范围的M2和Res，固体振荡所诱导的外部声流结构进行了综述性分析。

Bertelsen等[16]重新考虑了Holtsmark给出的不可压缩流体中圆柱附近的稳流理论，并详细讨论了两个同轴圆柱体间的声流，其中内圆柱体处于振荡状态。Bertelsen通过改变雷诺数、振幅和圆柱半径等参数得出了新的理论和实验结果，并与之前的观测结果进行了比较。图2给出了不同半径比A/a同轴圆柱体间的声流结构，内柱半径a=0.147 cm±1%，振荡频率为100 Hz±2%，运动黏度v=0.15 cm2/s±2%，ε=1/11±5%。研究表明，随着半径比A/a增大，边界层内的涡流尺度逐渐减小，而边界层外的涡流尺度逐渐增大。

图2 不同半径比同心圆环间的声流结构:A/a=2Fig.2 The structure of acoustic streaming between concentric rings with different radius ratio:A/a=2

Miyagi等[17]从理论上研究了圆柱在静止无限黏性不可压缩流体中做非简谐振荡诱导的定常流。在无量纲振幅和边界层厚度都很小的情况下（即满足ε＜＜1和M2＞＞1），发现圆柱周围的振荡边界层外会出现缓慢稳定的二次流。研究表明，一阶量O（ε）诱导的定常流在振荡方向上是对称的，在无穷远处消失；而当圆柱做非简谐振荡时，圆柱附近诱导的稳流对称性被破坏，但在距离圆柱无穷远处任保持具有对称特性的均匀流。图3给出了在x方向做非简谐振荡在圆柱外诱导的二次流型。

图3 圆柱作非简谐振荡引起的二次流Fig.3 Secondary flow caused by cylinder anharmonic oscillation

Riley[18]应用高阶边界层理论的方法，研究了在自由静止流体中作简谐振动的圆柱体周围引起的稳态流。将理论预测结果与高流雷诺数（Res＞＞1）下的实验结果进行了比较，进一步改善了理论模型，并对Bertelsen观察到的实验图像和理论之间的差异给出一定解释。Haddon等[19]研究了不可压缩黏性流体在外圆柱固定和内圆柱垂直于发生器作小振幅谐波振荡时诱导的同心圆间的稳态流动。在适当的流雷诺数（Res＞1）下，基于N-S方程研究了这种运动的时间无关分量。在柱坐标下，利用涡量流函数法求解了全N-S方程得到了声流流函数表达式。所得结果与Bertelsen的实验观测和早期理论具有很好的一致性。当Res＜＜1时，Haddon给出了式（9）稳态流函数解的形式，而为了得到式（9）对任意Res值的解，Haddon采用涡流函数方法，将稳态问题视为一个非稳态问题，对时间进行数值积分，直到达到期望的稳态解。图4给出了Res分别为0，90第一象限内的声流结构。随Res逐渐增大，涡的中心远离圆柱。

图4 稳定流的流线Fig.4 Steady flow streamline

Tatsuno[20]对浸入黏性液体槽中分别做简谐和非简谐振荡的圆柱体在其周围诱导的二次流进行了可视化研究。Tatsuno经实验验证了Miyagi等的理论模型，同时探究了圆柱体做非简谐振荡诱导的稳定流流场特征，并与做简谐振荡做了对比。研究发现，除了外涡流，单向流的组成部分还与振荡方向平行。圆柱直径d=0.604 mm，振动频率f=10 Hz，M2=ωd2/v=159。

图5 振荡圆柱诱导的二次流Fig.5 Secondary flow induced by oscillating cylinder

Dohara[21]对外圆柱作旋转振动（U2cos（ω2t+ϕ））和内圆柱作小振幅平动振动（U1cos（ω1t））诱导的二次流进行了理论分析，在满足ε＜＜1和M2＜＜1的条件下，采用逐次逼近的方法得到了二次流的解析表达式。研究发现，随r2/r1增大，环形圆柱间的声流流线大不相同。速度振幅比U=U2/U1越大，外圆柱内表面将诱导出尺度较小的涡流，而在内圆柱附近出现尺度较大的涡流。当U0=0时，即表明外圆柱固定不动，环形圆柱间诱导出四个轴对称的涡流，这与前人的实验即理论研究相一致。Zapryanov等[22]研究了两个半径分别为a和b的平行圆柱在i）平行或ii）垂直于包含其轴线的平面上振荡时所引起的稳流场，并采用匹配渐近展开的方法，分析研究了液力相互作用对稳态流场的影响。研究发现，当a=b（在i的情况下）时，稳定流对称地指向圆柱，而当a≠b（在i的情况下）时，二次稳定流则指向大圆柱，其中一个外稳定涡消失。在情形i）中，作用在每个圆柱上的阻力比作用在无界振荡流中具有相同半径的单个圆柱上的阻力小。当圆柱半径相等时，前圆柱体的阻力大于后圆柱体。相反，在情况ii）中，当a=b时，表明两个圆柱体上的每个阻力大于作用在无界振荡流中具有相同半径的单个圆柱体上的阻力，并且每个圆柱体在垂直于振荡流的方向上都经历排斥力。Lee等基于Nyborg理论，计算了驻波声场中圆柱黏性边界层外的声流流函数的显示表达式，计算表明，当圆柱位于声压波节位置时，其外部声流关于圆柱呈轴对称分布；而当圆柱偏离声压波节位置时，其对称性被破坏。如图6所示。

图6 圆柱边界层外的声流图谱Fig.6 The acoustic streaming pattern outside the cylindrical boundary layer

Yan等[23]用数值方法和实验方法研究了圆柱叶栅在无边界、不可压缩的黏性流体中做小振幅振荡诱导的稳定流动。数值结果表明，对于较小的流雷诺数Res，在叶栅的每个圆柱周围有四个等强度的循环流动，而当Res值较大时，不对称流动的对称性被打破。通过数值计算，确定了Res的临界值Res0，即Res＜Res0时流动是对称的，Res＞Res0时流动是非对称的，这些结果与实验结果符合得很好。Suh[24]分析了在满足ε＜＜1，M2＞＞1和Res＜＜1条件下，通过建立求解势流和Stokes流的级数方法，研究了两个串联圆柱周围二维Stokes流产生的声流，并考察了震荡方向Φ、圆柱间距d和圆柱直径D对声流结构的影响。Nuriev等[25]基于Open-FOAM开源代码研究了在黏性不可压缩流体中圆柱体周围声流随振动过程控制参数变化的演化过程。Bahrani等[26]利用PIV技术可视化了在流体中做自激振动圆柱诱导的黏性边界层内、外的涡流结构。

基于国外的研究现状，国内浦群等[27-34]也对上述类似问题及偏心环形圆柱间的稳流问题进行了相应的理论和实验研究。邓迪等[35]基于OpenFOAM开源平台自主开发的具有重叠网格功能的CFD（computational fluid dynamics）求解器naoe-FOAM-SJTU，对在静水中做周期性振荡运动的二维刚性圆柱涡激振动进行数值模拟。姜根山等[36]基于Lee等关于圆柱边界层外的声流理论对电站锅炉换热管外的声流进行简单数值计算。袁昱超等[37]提出了一种时域预报数值方法对振荡流下柔性立管涡激振动时域响应特性进行了预报，该方法可以表现出定常流特性，并捕捉到振幅调制、迟滞、频率转换及高频谐振等现象。

综合以上国内外研究方向分析知，二维圆柱体外二次流问题的研究分为三种:①单圆柱体在无界黏性不可压缩流体中做自激振荡诱导的二次流；②同心环形圆柱间的二次流；③双圆柱串联作自激振荡诱导的二次流。以上三种问题都局限在小振幅（ε＜＜1）简谐振荡或非简谐振荡的条件下，对于大振幅（ε＞＞1）振荡诱导的二次流问题还未涉及，且对于三维问题也尚待研究。此外，以上问题的研究大多是基于圆柱体作自激振荡诱导的二次流问题，而对于其反问题，声波（或其他原因）引起的振荡流与静止圆柱体间的相互作用的问题尚未研究。对于声波引起振荡流的问题，需要考虑更多的物理问题，如圆柱体的散射现象等，尤其对于多排管阵列问题的研究将是未来研究的热点问题。

2.2 二维球体外声流的流场结构

强声波作用下煤粉颗粒外部的声流效应对促进煤粉完全燃烧，强化煤粉颗粒、颗粒间的热传导和煤粉颗粒与烟气之间传热传质过程具有重要作用。因此，关于振荡流场中球形颗粒边界层内外的声流一直受到研究者们的关注。

早在1888年，Basset[38]便对处于振荡流中球体上的一般问题进行了理论研究。之后，Odar等[39]对球体上的振荡流动进行了实验研究，试图修正Basset的理论解。Lane[40]基于Raney圆柱外的声流理论模型修正了球体外的声流模型，并将观测到的边界层厚度与理论计算得到的边界层厚度进行了比较，对理论进行了实验验证，并将应用于圆柱问题的方法在一定程度上用来修正球面问题，修正后的结果与已有的实验观测结果基本一致，同时进一步证明了Rayleigh提出的扰动理论作为处理二阶现象是一种有效的方法。Lane给出了二维球体外的声流流函数方程:ψ2=f（r）sin 2θ，该方程与圆柱体外流函数方程类似。根据流函数方程可得到二维球体外的稳流流线图，并与圆柱体做对比。从图7中看出，圆柱体的内涡在45°线上具有对称性，而球体则没有这种对称性，因为漩涡的中心位于54°43′线上。

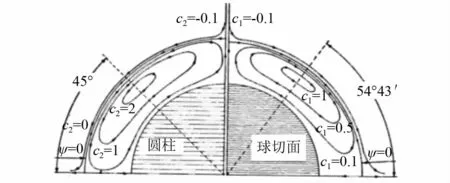
图7 二维球和柱体边界层声流结构对比Fig.7 Comparison of acoustic streaming structure between two-dimensional spherical and cylindrical boundary layer

Dohara[41]针对Re＜＜1的情况，研究了球体在静止无界黏性流体中作谐波振荡诱导的二阶声流，给出了定常流的流线型及瞬时流线，并对球体表面的阻力进行了计算。Rednikov等[42]在介质不可压缩限制下，研究了流体介质和沿椭球体对称轴作小振幅高频相对振荡运动时诱导的声流问题，分析了Stokes剪切波层的内部流型和外部流型，并对小雷诺数情况下的流场进行了解析求解。在较大的雷诺数下，考虑了边界层的影响，系统地研究了圆盘有限区域中的稳态流动，并讨论了非扁球形状的定性意义。Kotas等[43]实验研究了在Re＞150，ε≤1.2的情况下，不同纵横比的球形颗粒在黏性流体中振荡诱导的稳定流。利用沿球体中心平面的相位锁定粒子路径线图像，可视化了流动的稳定流成分，如图8所示。研究发现，以驻点的距离为特征，声流区域的大小取决于一个基于球体长宽比和等效半径的长度刻度，这些斜振动球体表面驻点的角位移与长径比和振动角有关。

图8 椭球外的声流结构Fig.8 Acoustic streaming structure outside the ellipsoid

Alassar[44]建立了振荡流场中球形颗粒外的声流模型，通过数值求解N-S方程，研究了振荡流通过球面时产生的声流现象。研究表明，随雷诺数Re和斯特劳哈尔数Sr的增加，边界层内涡流尺度减小，边界层外涡流尺度增大。Valverde[45]基于不可压缩N-S方程对直径为10～1 000μm颗粒外声流的主要特性进行了分析，考察了介质振幅ζ0、颗粒半径R和Stokes边界层厚度δv综合效应对颗粒外声流分布规律的影响。Baasch等[46]建立了球形液滴或气泡颗粒内部和外部声流的解析理论，但并不适用于固体颗粒声学边界层内的声流分析。

由以上的研究可知，二维球体外的声流结构和圆柱外的声流结构很类似，但在空间分布上存在差异，这是由流函数方程决定的。而目前国内对球形颗粒外，尤其是椭球型外的声流特征研究还未见报道。此外，考虑多颗粒间的相互作用对声流结构的影响将是未来研究的主要方向。

2.3 二维矩形空腔中声流的流场结构

针对二维空腔中的声流研究，1884年首次由Rayleigh在《On the Circulation of Air Observed in Kundt’s Tubes》一文中进行了研究，并第一次给出了声流的理论解形式。Rayleigh的工作极大地推动了诱导声流现象本质机理的研究。在满足kLy＜＜1的条件下，墙壁边界层内的声流相对于边界外的声流尺度很小，因此在数学上处理上，Rayleigh给出了Kundt’s Tubes存在驻波声场诱导边界层外的声流流函数及二阶流速理论解。

基于Kundt’s Tubes结构模型，如图9所示，后期研究者们进行了丰富的实验和理论研究。日本学者Arakawa等[47]研究了封闭管内空气柱有限振幅振荡引起的非线性现象——声流。在管道内，有限幅值振荡所产生的强驻波由于壁面摩擦损耗会产生声流现象，因此作者详细分析了振荡边界层对激波的响应。而声流的速度是由正弦振荡扰动展开的二阶项的稳定部分来估计的，将四阶空间差分法应用于声流的二维分析，计算结果显示了振荡边界层内的速度分布和不同振幅下的稳态流场结构，并考察了有限振幅振荡引起冲击波在管道内的传播。吴嘉等[48]利用流动显示和LDV（laser doppler velocimetry）技术，对驻波管中高强驻波声场诱导湍流问题进行了实验研究。实验结果表明，当反射端声压级高于140 dB时，驻波管声流旋涡结构会发生变化，且随着声压级的提高，管中规则稳定的旋涡结构逐渐变化，出现合并、破裂等现象，在高强声下声致流动开始呈现出一定的湍流特性。之后，吴嘉等[49]对声压级大于160 dB时，驻波管中的声流特性进行了实验分析，进一步验证了高强声作用下稳定对称的旋涡结构将被破坏，并伴随着旋涡的拉长、合并、破裂等现象的发生，驻波管内将产生复杂的湍流结构。

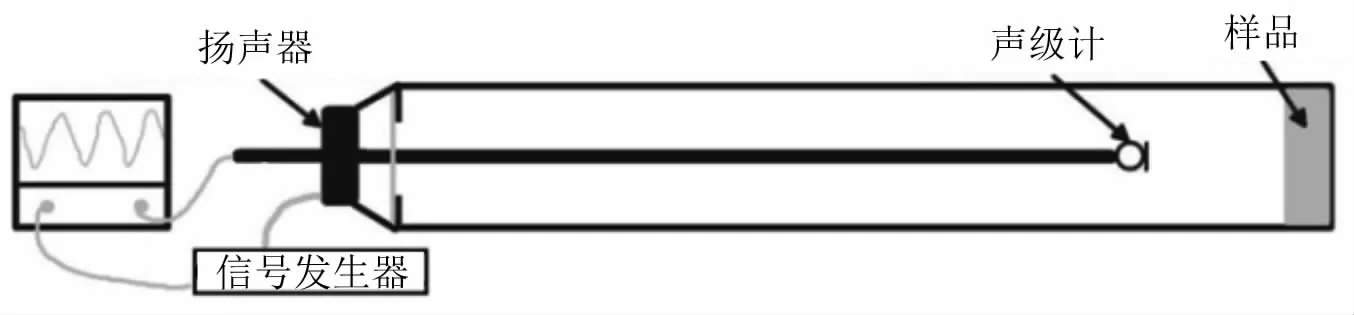
图9 Kundt’s Tubes模型Fig.9 Kundt’s Tubes model

Hamilton等[50]给出了任意宽度二维通道内黏性流体中驻波声流的解析解，准确地描述了边界层内外的Schlichting流和Rayleigh流，如图10所示。对于宽通道和边界层外的情况，解析解与经典Rayleigh流的解一致，且随着通道宽度的减小，Schlichting涡相对于Rayleigh涡的尺寸增大，当通道宽度小于约10倍边界层厚度时，Rayleigh涡消失，只有内涡存在。并将所得解与Rayleigh、Westervelt[51]、Nyborg和Zarembo的解进行了比较，验证了解析解的正确性。

图10 二维矩形通道中的声流结构示意图Fig.10 Schematic diagram of acoustic streaming structure in two-dimensional rectangular channel

Aktas等[52]对由可压缩气体填充的二维矩形封闭空间中的声流运动进行了数值模拟，研究了声场强度对流动结构形成过程的影响。振荡流场是由左壁的振动产生的，且壁面振动频率的选择应确保最低声振型沿外壳传播。Aktas等考虑了N-S方程的完全可压缩

形式，采用显式时间推进算法对声波进行跟踪，计算并全面描述了封闭空间中波场的形成，预测了声边界层的发展。通过对给定周期内的解进行时间平均，揭示了波场与黏性效应的相互作用和声流结构的形成，并发现与声效应相关联的压力波的强度和由此产生的声流流型与振动周期期间壁的最大位移密切相关，且波形决定了振荡流场中稳定流结构的形状。Nabavi等[53]实验研究了不同加热水平壁面对声驻波作用下充气矩形箱体内声流速度场的形状和幅值的影响，并采用同步粒子图像测速技术对流动速度场进行了测量。结果表明，上下壁温差使对称流动涡变形为非对称流动涡，且随着温差的增大，流动速度的幅值增大。雷洪等[54]基于边界层理论，建立边界速度数学模型研究矩形管道中Rayleigh声流现象。此数学模型采用3阶谱元方法求解，驻波声场对流体流动的影响采用壁面处的声边界速度来表达，同时引入雷诺数来分析非线性项和黏性项的重要性。数值结果表明，在2维和3维情况下，声边界速度模型均与近似解相符，声边界速度模型和近似解的差异来源于对非线性项的处理，与近似解相比，声边界速度模型的优势在于能考虑流体流动的非线性效应且仅要求矩形管道的特征尺寸的2倍小于波长；在2维情况下，回流区的涡心位于管道高度的1/4；而在3维情况下，回流区的涡心则靠近壁面。在壁面附近，非线性项的影响不能忽略；而在上下2个涡心的中间位置，非线性项比黏性项更加重要。周天等[55]采用多松弛时间格子玻尔兹曼方法（multiplerelaxation-time-lattice Boltzmann method，MRT-LBM）

对二维平板间的驻波声流进行有效数值模拟，并考察了流体黏度和板宽对驻波声流的影响。研究表明，流体黏性主要影响边界层内部声流，对主流区域，特别是通道水平中线附近区域的声流影响较小，随着黏度增加边界层内声流幅值会明显升高，边界层内声流能量所占比例明显增加。

由以上的研究现状表明，二维矩形通道中声流流场结构的研究受到了国内外学者重视，并基于Kundt’s Tubes模型得到许多新的物理现象。以上的研究考虑了二维矩形通道的几何尺寸和激励频率、激励源强度以及温差对通道内边界层内Schlichting流和边界层外Rayleigh流流场结构的影响，但没有考虑来流的影响，因为声流是二阶小量，容易被来流淹没。此外，通道内诱导的声流现象用于加强物质掺混及粒子操纵是当前研究的热点问题[56-60]。

3 声流强化传热传质的研究

声流流场结构研究的目的在于理解强声传热的机理，并根据结构场环境利用合适的声流来改善热、质传输过程。强声作用下声流效应对传热行为的影响程度通过定义流雷诺数来描述

式中，us为物体几何模型Stokes边界层外表面上的滑移速度，该速度将边界层内外的声流运动区分开来。对于不同的几何模型，us的取值不同，但总满足关系:us～/（ωR）。

3.1 二维圆柱外声流强化传热传质分析

圆柱管外的传热行为分析具有工程应用意义。众所周知，具有管阵列结构形式的换热器在工程中具有十分广泛的应用，而如何提高其传热效率是工程界和学术界亟待解决的关键技术问题。

Richardson[61]在声波波长远大于圆柱直径的条件下，对圆柱在静止流体中做横向周期性振动诱导的声流对流传热问题进行了分析，并给出了适用于大范围普朗特数（Pr）的解，并区分了小流雷诺数Res（min）和大流雷诺数Res（max）情况。研究表明，在自然对流影响较小的情况下，理论分析结果与实验结果吻合较好，且热边界层厚度δth和黏性边界层厚度δv的相对大小是分析物体传热行为主要依据，Pr～δ/δth。Davidson[62]给出了恒温圆柱在静止无界黏性流体中做周期性小振幅振动的传热理论结果，并考虑了小流雷诺数和大流雷诺数条件下圆柱外的传热行为。Davidson基于Richardson的传热分析和Riley的流场研究，进一步改进了圆柱外传热关联式适用的普朗特数Pr范围，并给出了边界层外的稳定流流函数微分方程和相应的稳态温度场微分方程。Haddon等[63]研究了不同温度同心环柱间的传热行为，其中内柱做小振幅谐波振动，外柱静止不动，经数值计算得到了表征它们的三个参数（即圆柱直径比、流雷诺数和普朗特数）范围内环柱间时间平均速度场和温度场控制方程的数值解。研究表明，声流运动增加了热量的传递，且在某些情况下，环柱间的传热效果是显著增加的，超过了仅靠热传导可能达到的传热效果。Mozurkewich[64]采用瞬态法对不同直径热导线处于管中驻波声场速度波腹位置时的传热进行了实验测量，由关闭加热后的温度变化率推导出换热速率。实验发现，对于固定导线直径和声频率，无量纲传热系数Nu随声幅值变化明显，在高振幅时，Nu由稳态流、强迫对流决定，而在低振幅时，Nu有一个由自然对流决定的恒定值，并当流雷诺数Res=88时，这两种状态之间的过渡相当突然，这种现象Mozurkewich通过声流效应进行了阐述。Gopinath等[65]对强声场中圆柱的对流换热行为进行了实验研究，并确定了两种不同流动状态下的传热行为关联式:第一种是圆柱外稳定的层流附加流态，努塞尔数（Nu）与流态雷诺数（Res）的平方根成正比；第二种状态是不稳定的湍流流态，圆柱背部旋涡脱落是普遍存在的，该状态进一步提高了传热率。对于大Res值，这种行为似乎表明了一种更强有力的热传输机制，这种机制不能仅仅由层流边界层对流效应引起，可能是由于边界层分离导致涡流脱落和相关的传输速率增加所致，因此，两种状态的传热行为将由临界流雷诺数Rescriti来区分。

姜波等[66-68]采用数值模拟与实验相结合的方法，研究了低频振动管外的流动与传热特性。研究表明，振动有利于强化传热，且其强化传热的效果随着振动频率与振幅升高而增强。宿艳彩等[69]基于Fluent动网格及UDF编程技术对二维流场中振动圆柱的换热特性进行了研究。结果表明，当圆柱振动速度幅值大于来流速度时可以强化传热。刘健华等[70]通过求解二维非定常雷诺时均N-S方程，对二维管内可压缩流动模型进行数值模拟，分析壁面振动对流场及传热的影响。研究发现，壁面局部振动对下游流场造成一定扰动，但在传热方振动的壁面只在一定的相位区间才能增强换热。吕平等[71]利用实验的方法研究了水平圆管在高频低振幅的横向振动条件下，管内流体的传热特性。实验结果表明，随着振动频率的增加管内对流换热系数先增大，达到峰值（共振频率下）后迅速减小，最终趋于稳定。

由以上的研究现状分析知，对单管做自激振动传热行为的研究还是目前的研究热点。但局限于换热器结构的固定性，导致换热管本身的振幅受限。因此，利用声波引起的振荡流对单排和多排管阵列传热行为的研究将是未来探究的热点问题。

3.2 二维球外声流强化传热传质分析

对颗粒传热传质行为的研究最早要追溯到20世纪中期，Morse[72]首次经实验证明了，低频率（50～500 Hz）、高强度（＞110 dB）的声波能明显改善细粉体的流化质量，并对声波在大型流化塔中的应用提出了建议。基于此，国内外进行了许多利用声波改善流化床床料流化质量的实验研究和仿真计算，但对于声波改善流化行为的机理研究还有所欠缺[73-76]，且没有涉及声流运动的影响分析。

基于球形颗粒外声流流场结构的分析，Gopinath等[77]研究了大流雷诺数条件下声流对球体的对流换热，采用解析和数值求解技术，获得了努塞尔数Nu与大范围普朗特数Pr的关联式，并通过实验验证了关联式的正确性。Gopinath的分析始终满足ε＜＜1，即确保颗粒外不发生边界层分离，流动始终保持层流状态。在流场分析过程中已证明，ε作为一个小扰动参数，对于采用匹配渐近展开的方法使控制方程在分析上易于处理。对于较大的普朗特数，热边界层在速度边界层尺度上非常薄。当热边界层嵌在速度边界层内时，Stokes区外缘的流动速度对换热起主导作用；而对于非常小的Pr数，热边界层在速度边界层尺度上非常厚，温度的变化更为缓慢，并延伸到速度边界层尺度以外的区域，在该区域中，稳定的切向速度基本上不存在，并且只有边界层流动典型的径向向内的稳定漂移速度，因此只有这种夹带速度引起的对流效应才有可能平衡速度边界层外热量的扩散效应。Alassar等[78]研究了等温球处于振荡黏性自由流中的热对流问题，考虑了在强制对流和混合对流两种情况下。通过求解Pr=0.71的Boussinesq流体非定常N-S和能量方程，考察了Re，Gr和St等无量纲参数对球外对称流场和温度场的影响。Kiani等[79]进行了超声辐射置于混合溶液中铜球的冷却实验研究。研究表明，超声辐射能够显著提高冷却介质中铜球的传热速率，且超声强度的增加导致冷却速率的加快。此外，空化和声流都是强化传热的重要因素。Ha等[80-81]通过数值方法计算了二维非稳态N-S和能量方程，并给出了不同振荡流作用下球形颗粒表面的速度场和温度场分布。计算表明，在声雷诺数Res大约为100时，相比于无声场，努塞尔数增加了290%。

国内许伟龙等[82-84]通过实验和数值计算研究了强声波作用下夹带在烟气中单颗粒煤粉的传热特性，分析了声压级为145～167 dB，频率f分别为50 Hz，1 000 Hz和5 000 Hz时，颗粒壁面传热的效果。研究表明:颗粒传热速率随振荡速度幅值的增大而增大，当声压级为167 dB，f=5 kHz时，颗粒的时间-空间平均努塞尔数是无声场时的1.78倍。数值和实验结果均表明，声场能显著地增加传热，且声压级越高，传热速度越快。

通过3.1节和3.2节的分析知，二维圆柱和球体外声流对传热行为的影响，在小流雷诺数条件下，努塞尔数Nu与流雷诺数的平方根成正比:Nu～；而在大流雷诺数条件下，努塞尔数Nu与流雷诺数满足关系:Nu。这表明，流雷诺数越大，物体换热效果越好，该关联式对指导工程应用具有重要意义。

3.3 二维矩形通道中声流强化传热传质分析

二维通道中的声流传热问题一直是研究的热点，主要研究可见于微器件内热消除技术。Gopinath等[85]基于“Kundt’s Tube”模型，研究了声流在驻波中的对流换热问题，利用数值求解软件PHOENICS求解了由流体运动引起的完全椭圆形式稳定输运方程，并对声学特征和几何变量的影响进行了参数化研究，建立了空气的Nu数关联式:Nu=0.27Re0.5s，且声流引起的对流换热率由Kundt’s Tube两端的温差决定。Aktas等[86]数值研究了存在温差的二维封闭通道中由垂直侧壁振动引起的热对流问题，考虑了N-S方程的完全可压缩形式，并采用显式时间推进算法对声波进行跟踪和高精度的通量修正传输算法得到了数值解。研究表明，稳态二阶声流结构对传热速率的影响比主振荡流场更为显著，声流在零重力环境下向系统引入了额外的对流换热模式。Lin等[87]采用数值模拟方法研究了水平壁差热充气密闭空间的传热问题，采用高精度的通量修正输运算法求解了N-S方程的完全可压缩形式，且数值模型中考虑了温度对导热系数和黏度的影响。数值模型中一个侧壁以指定的频率和振幅振动，以诱导封闭室内的强制对流流动，振动壁和固定壁被认为是绝热的，两个水平壁是差热的。研究发现，声流的存在对传热有显著影响，且封闭室内温度梯度的存在会影响声流的形成，其对称结构被破坏。Aktas等[88]研究了二维封闭空间中驻波声场诱导的典型和不规则声流运动对对流换热的影响，考虑了N-S方程的完全可压缩形式来计算振荡流场和平均流场，并采用基于控制体积法的显式时间推进流量校正传输算法模拟了封闭空间中的传输现象。流体运动由左壁的周期性振动驱动，右垂直壁是绝热的，而上、下水平壁保持一定温差。研究表明，横向温度梯度对声流结构和速度有很大影响，与纯热传导相比，声流运动显著增强了底部壁面的整体传热；而在不规则流的情况下，增强效果更为明显。Tajik等[89]实验测量了水平受热面上充水封闭圆柱壳在声流作用下的强化传热。利用超声栓接式Langevin换能器，由下板振动引起声流，上板作为存在热源的反射壁在与振动板之间产生驻波。上板采用恒定热流加热，侧壁保持恒定温度，忽略了重力对流场的影响，传热强化是由于振动引起的。实验中考虑了换能器功率、加热器高于振动板的高度和加热器热流密度的影响。实验结果表明，在超声振动产生的声流作用下，热源与振动板附近的水之间的传热强化可达390%，传感器功率的增加和加热器高度的降低导致外壳内的传热系数更高。

国内刘峰等[90]利用时空守恒元解元算法应用于二维平板内驻波声流的计算，通过对比自然对流换热来研究驻波声流对二维平板内对流换热的影响。数值计算表明，二维平板内驻波声流能明显的加快对流换热，有效的降低流场中的热量。

据以上的研究现状分析知，对二维矩形通道中声流传热行为的研究是国外学者关注的热点问题。而国内对该问题的研究还相对落后。随着电子技术朝着更高的集成密度和更高的功率器件的方向发展，利用声表面波驱动微空腔中的声流运动来消除微电子的发热问题是当前研究的热点问题。

3.4 声流强化传热声学参数分析

由3.1～3.3节的分析知，振荡流与物体之间非线性相互作用诱导的声流运动对传热行为的影响，可通过努塞尔数Nu与流雷诺数Res之间的关联式进行描述

式中，因子A0和指数n与普朗特数Pr的值关系不大。对于空气，Pr=0.7～0.8＜1，这意味着热量与动量相比扩散的较快，这时A0=1，n=0.5。 由式（13）可知，扰流雷诺数Res越大，外传热效果越好。而对于不同物体几何模型和介质流场特性，A0，m，n取值不同。

从Res=/ωv的定义可以看出，流雷诺数与固体的几何尺寸无关，完全由声波的特性和传播介质的特性决定。声强级的定义由以下方程给出

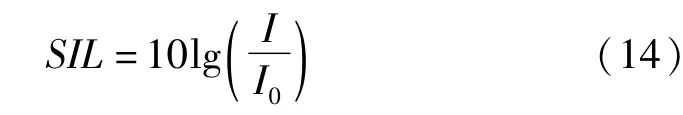
式中:I0为参考声强，10-12W/m2；I为平面驻波声强，由以下公式定义

根据式（14）和式（15），利用流雷诺数Res重新定义SIL，即

联立式（13）和式（16），推导出如下关系式

式中，ω0为无量纲角频率，ω0=ρcvω/（2I0）。 因此根据式（17），可用声强级来确定固体外的流雷诺数。结合式（17）分析可知，努塞尔数与声强成正比，与振荡频率成反比，因此采用低频高强度声是强化物体传热传质过程的有效方法。

4 结 论

根据以上研究现状分析知，国外对声流进行理论研究最早追溯到19世纪80年代初，相比之下，国内对声流的研究要落后很多，无论是在理论还是实验研究方面。这种基于小振幅振荡诱导的稳定涡流现象，经联合连续性方程和引入流函数，严格求解了非线性Navier-Stokes动量方程获得了与时间无关的稳定解。并通过声流现象的可视化实验，对理论模型进行了验证。而鉴于以往理论研究和研究手段的局限性，目前的研究还停留在对几何模型相对简单和物理场环境相对单一声流现象的探究。仅对声流流场结构进行简单的描述，而没有进一步对声流强度、声流运动范围等重要流场信息进行研究。但随着科学技术的进步，声流研究的手段呈现多样化，主要包括:①数值模拟。（i）使用多物理场耦合（如温度场-流场-声场之间的耦合）有限元软件COMSOL Multiphysics实现复杂物理场环境中的声流数值求解；（ii）利用OpenFOAM开源平台实现N-S方程组的直接求解，但该方法仅适用于简单几何形状的物理模型。②实验研究。利用PIV技术可实现任意几何模型外声流结构场的可视化和流速测定。因此，采用COMSOL软件实现复杂环境场中包含微观物理场信息（如声学边界层内的物理场）的声流模拟和利用PIV技术捕捉声流的宏观物理场行为将是未来研究的主要手段。

鉴于此，未来对声流的研究更应着眼于具有工程应用背景的复杂物理场和结构场环境，及考虑声学参数的影响。如:①三维物体外声流流场结构分析；②考虑颗粒间相互作用的多颗粒间声流流场结构及传热行为研究；③换热器管阵列结构中的声流流场分布及强化传热研究；④考虑多物理场耦合作用下（如耦合流场、温度场等），声流流场结构的变化；⑤声流和声辐射力协同作用下颗粒动力学特性研究；⑥强声作用下的声流现象，需考虑更多的声学问题，如物体的散射及管整列结构中的“导带”和“禁带”问题；⑦考虑大振幅（ε＞＞1）诱导的声流行为，目前对声流现象的研究还局限在小振幅（ε＜＜1）条件下，可推断，大振幅振荡诱导的声流由于强的非线性作用将出现不同于小振幅的物理现象。此外，声流效应用于微电子设备中的热消除和操作微颗粒动力学行为（声镊子）的研究是当下的热点问题。