十二次二维准晶圆形弧段裂纹的热应力分析

马园园，赵雪芬，丁生虎

（1.宁夏大学 数学统计学院，银川 750021；2.宁夏大学 新华学院，银川 750021）

随着耐高温复合材料在工程实际中的应用日益广泛，复合材料热应力问题的研究引起了许多力学工作者的关注。Kattis等[1]采用二相复势的方法研究了曲线边界夹杂的平面热弹性问题，得到了椭圆夹杂在无穷远处均匀热流作用下的热弹性场。文献[2]采用拉普拉斯变换和有限差分方法，研究了无牵引边界条件下多层圆柱的热弹性问题，得到了瞬态温度场和热应力场的解。文献[3]采用叠加法求出轴对称平面应变状态下正交各向异性空心圆柱的热弹性解。Wang等[4]利用解析延拓方法研究了两个不完全黏结的半平面内嵌任意形状热夹杂问题。

准晶作为一种新材料，具有硬度高、摩擦因数低、耐高温和耐磨等优良性能[5-6]。Li等[7]采用格林函数法研究了一维六方准晶的热弹性解。文献[8]研究了十次准晶复合材料椭圆夹杂的热应力问题。Guo等[9]利用Stroh型形式解，导出了均匀热流作用下含导电椭圆孔十次准晶的弹性解。文献[10]采用扩展位移不连续法分析了一维六方周期平面裂纹的热应力及裂纹尖端场的奇异性。虽然弹性材料中各种类型的热应力分析[11-13]以及含缺陷准晶体的力学分析[14-17]已得到较充分的研究，但准晶夹杂中含缺陷的热应力问题还未得到充分的讨论。

本文研究了十二次二维准晶在点热源作用下的共弧圆形界面裂纹的平面问题，分析了夹杂内外温度场，声子场及相位子场的热应力。由此导出了含有两条裂纹时，分区复势函数和应力场的封闭解。

1 问题描述与基本公式

如图1所示，无限大十二次二维准晶基体S-中包含一个半径为R的圆形准晶夹杂S+。在无限大准晶基体S-内任意一点z0作用着一点热源，其强度为q0。同时，在准晶基体与准晶夹杂界面上有n条互不相交的裂纹L′1，L′2，…，L′n，裂纹的尖端分别用aj和bj表示，记L′=L′1+L′2+…+L′n。 除裂纹L′外的剩余部分记为L，不失一般性，假设在L′上无面力作用。当准晶基体与准晶夹杂黏结完好时，在L上满足位移和应力连续的界面条件。

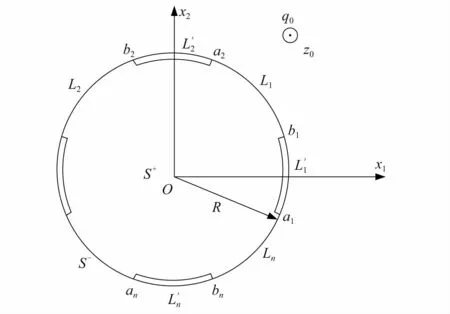
图1 点热源作用在圆弧界面裂纹附近Fig.1 The point heat source acts near the circular arc interface cracks

设准晶圆形夹杂的中心在复平面z=x1+i x2的坐标原点，则夹杂与准晶基体界面上的点可表示为t=Reiθ。此时，界面上位移和应力的边界条件可表示为

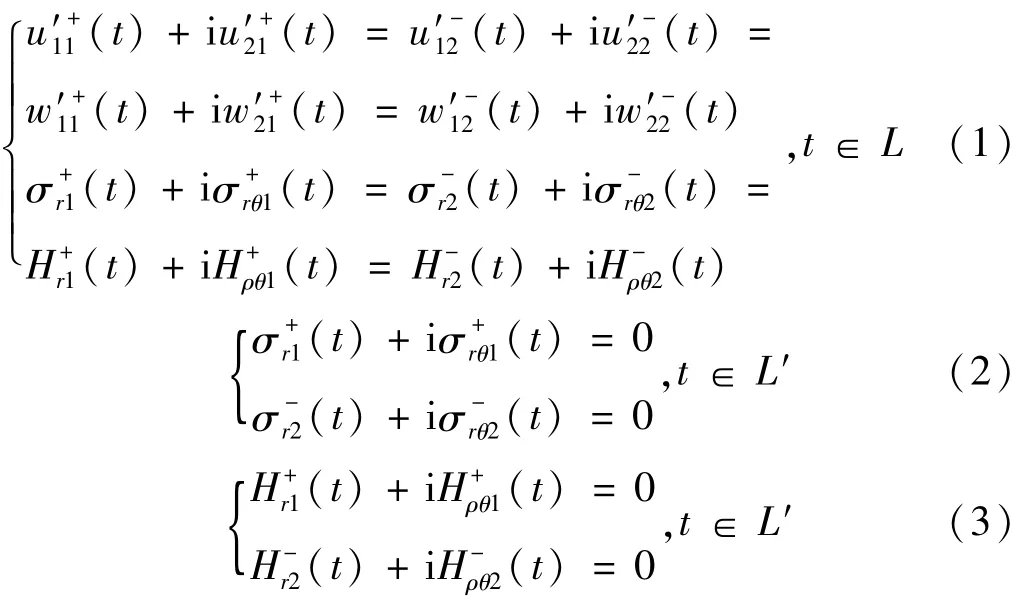
式中:σr，σrθ为极坐标中准晶夹杂和准晶基体声子场的应力分量；Hr，Hrθ为极坐标中准晶相位子场的应力分量；u1和u2为直角坐标系下准晶夹杂和准晶基体声子场的位移分量；w1和w2为直角坐标系下准晶基体与夹杂相位子场的位移分量；最后一个下标1和2分别为区域S+和S-；上标“+”和“-”为当z分别从S+和S-趋向于界面时函数所取的边界值。

由文献[18]知，夹杂和基体的声子场和相位子场可用四个复势应力函数 Ω（z），Θ（z），Λ（z） 和 Γ（z） 再加两个温度复函数g′1（z），g′2（z） 来确定，即

由二维热传导理论知，热流Q，热流强度q和温度T可以由单个复温度函数表示为

式中:κt为热传导系数；qx，qy和qρ，qφ分别为热流强度的直角坐标分量和极坐标方向的分量；Re和Im分别为对复数函数取实部和虚部。

2 温度场

准晶基体中的复温度函数可以表示为

令

则成立

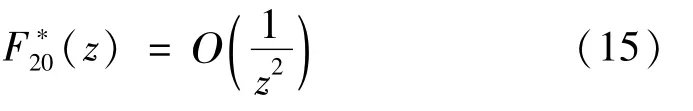
由推广的Schwarz镜像延拓方法[19]，可得

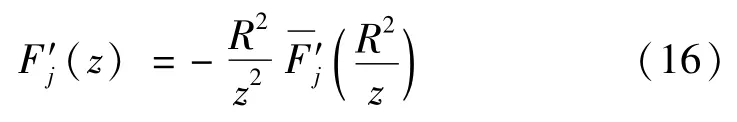
于是准晶基体S-中的温度函数F′2（z）经边界可延拓到S+内，表达式为

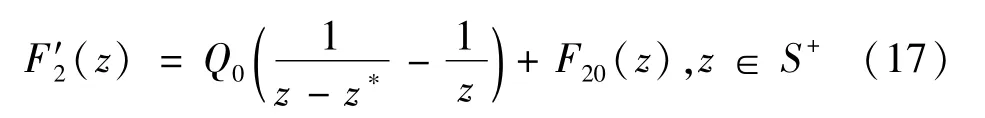
考虑式（14） 和式（17），函数F′2（z） 在沿边界割开的除z0，z*，∞和0点外的全平面全纯，则F′2（z）可改写为

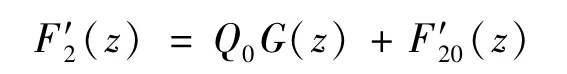
式中:Q0G（z） 为奇性主部；F′20（z） 为全平面内的全纯部分。其中

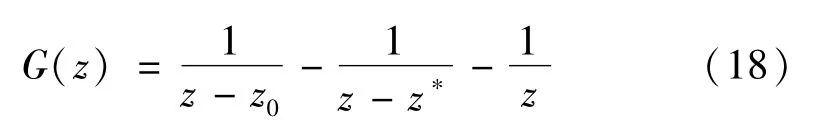
由于S+内无热载荷作用，则F′1（z）全纯，可用级数形式表示为

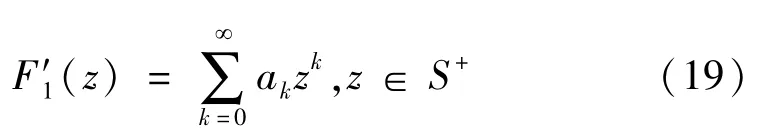
用上述方法将F′1（z） 延拓到S-内，有

在该问题中，考虑到界面裂纹是非渗透的，则在边界上热流强度和温度连续边界条件可表示为

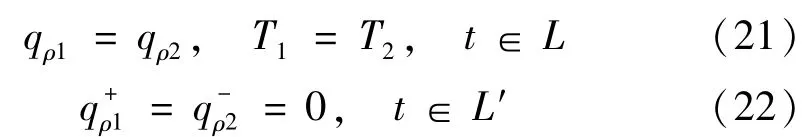
式中，qρ为径向极坐标下的热流强度。

由式（11）、式（13）、式（21） 和式（22） 可得

即

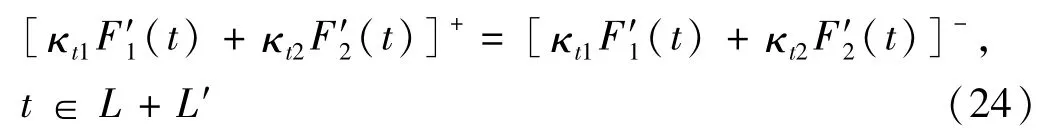
由推广的Liouville定理可得

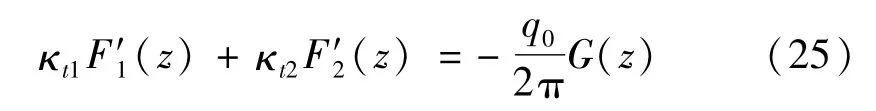
由式（10） 和式（21） 可得

对式（26）两边关于φ求导，有

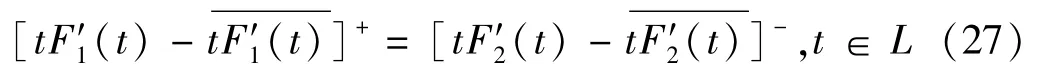
因为在边界L上有

从而成立

把式（28） 代入式（27），得到

再把式（25）代入式（29）的右边，得到

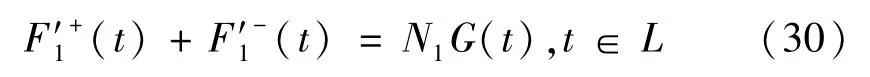
其中，

由文献[20]可知，边值问题式（30）的解为

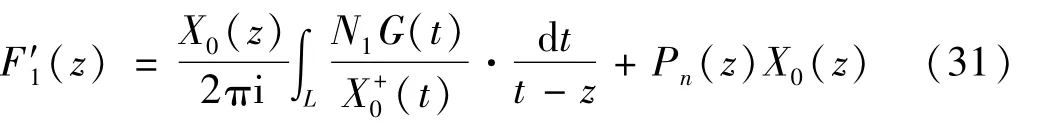
其中，

这里X0（z）是沿L割开的平面上的任一单值分支，且有

Pn（z）是与X0（z）在无穷远处性质有关的任一多项式，其一般形式如下

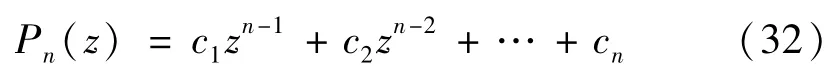
计算式（31）的积分，得到

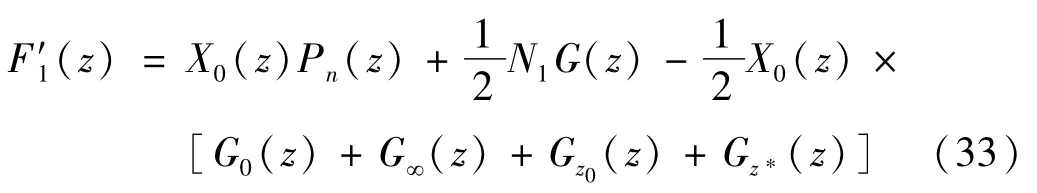
式中，G0（z），G∞（z），Gz0（z），Gz*（z） 为被积函数在z=0，∞，z0，z*点处的奇性主部。

对于式 （33），还需要确定n个常数c1，c2，…，cn。为确定这些常数，先把式（33）代入式（25），得到

把式（34）在无穷远域展开后与式（14）和式（15）比较前的系数，可得到有关方程，进而求得前的系数。

为了确保L上温度的连续性，还需要补充n个端点温度相等条件。先假定端点a1处温度确定，则可得到n-1个方程

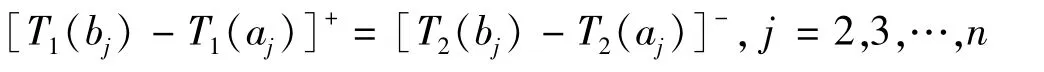
由式（25），可得

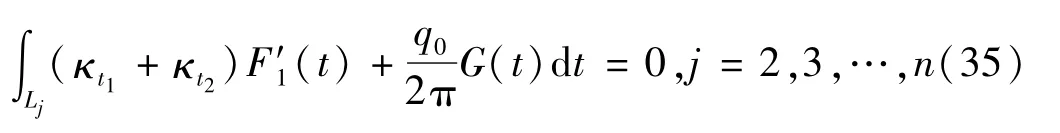
则式（35）是n-1个方程，可确定n-1个未知数，至此F′1（z） 和F′2（z） 可完全确定，这样表示整个温度场也完全确定。

3 声子场热应力分析

准晶夹杂和基体中的复势函数，设为

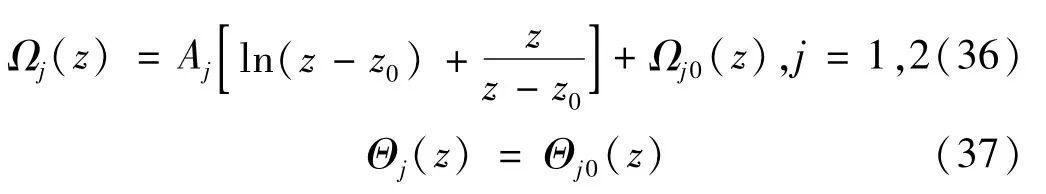
式中:Aj为实常数；Ωj0（z），Θj0（z） 为对应区域内的全纯函数，且在无穷远邻域内趋于0。

由声子场位移单值性可得

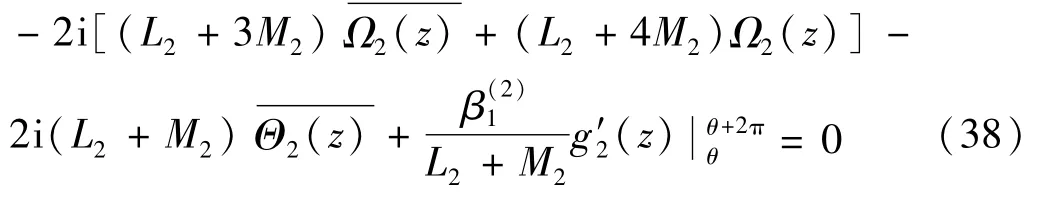
把式（36） 和式（37） 代入，由于ln（z-z0） 和互为共轭，模相同而辐角相反，从而得

式中，κt2为准晶基体中的热传导系数。

运用推广的Schwarz镜像延拓方法，在区域S+内定义延拓函数

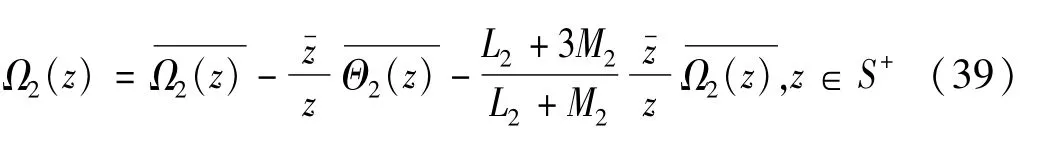
这样，Ω2（z） 可经过圆弧L′解析到S+内，把式（36）、式（37） 代入式（39），得到

对式（40）进行主部分析，得到Ω2（z）在全平面的表达式为

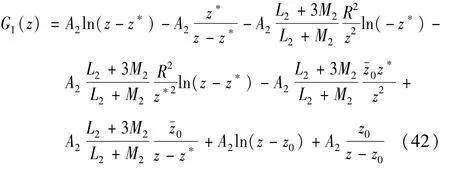
同理，在S-内引入函数

这样，Ω1（z） 可经过圆弧L′解析到S-内。

考虑边界条件式（1）、式（2），把式（39） 和式（43）代入，即得

即

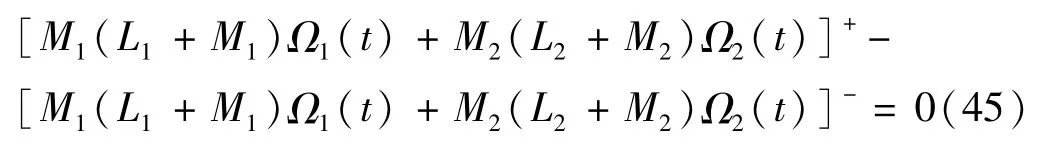
由广义Liouville定理，可得

式中，D0为常数。

由边界条件式（1）、式（8） 和式（43） 可得

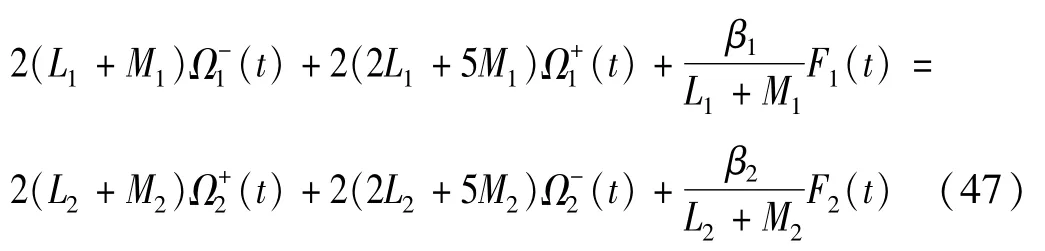
把式（41）和式（46）代入，整理得

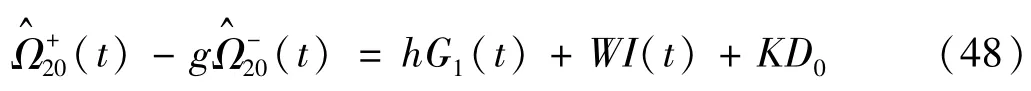
式中，g，h，K，W，I（t） 见附录A中式（A.1）。

这是一个R-H边值问题，它的解为

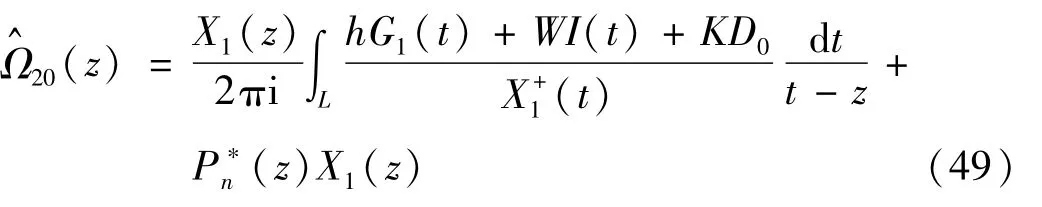
其中，

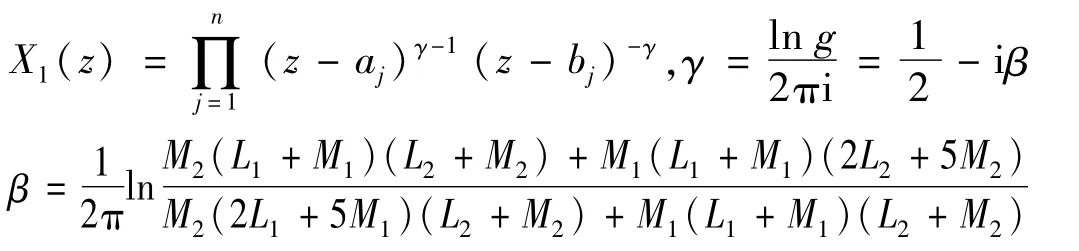
且X1（z）是沿L割开平面上的一单值分支，满足

P*n（z）为不超过n次幂的多项式

计算式（48）的积分后，再代入式（41）和式（46）后，即可得到 Ω1（z） 和 Ω2（z）。由式（39） 和式（43），可知

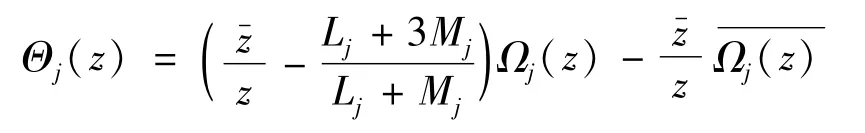
这样，准晶夹杂和准晶基体声子场的复势函数形式解已经求出。下面来确定c0，c1，c2，…，cn和D0这n+2个常数。由于无穷远处应力为0，得Ω2（∞）=0，则由式（41）和式（49）可得c0=0。

由于在无穷远邻域内

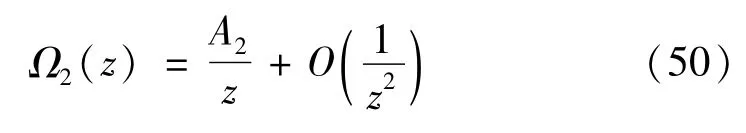
与式（41）在无穷远邻域内的洛朗级数展开式比较可得一个方程。

又考虑到 Ω1（∞）=D0，再代入式（43），即得

为了保证位移连续条件还需补充在n个端点位移相等的条件。考虑相对刚体位移，可假设其中b1重合，则有n-1个独立条件，由此可得

把式（41）、式（46） 代入整理得

式中，h1，h2，h3见附录A中式（A.2）。 至此，Ω1（z） 和Ω2（z）求得，声子场热应力可完全确定。

4 相位子场热应力分析

由于十二次二维准晶声子场和相位子场的不耦合性，相位子场在点热源q0作用下的热应力分析需进行计算。

设相位子场的复势函数为

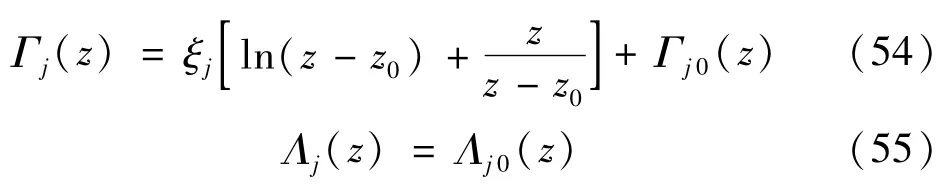
式中:ξj为实常数；Γj0（z），Λj0（z） 为S-中的全纯函数，且在无穷远邻域趋于0。

由相位子场位移的单值性可知

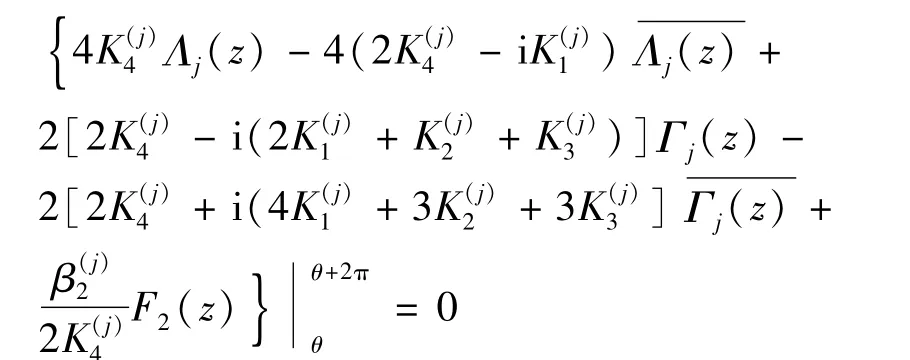
把式（54） 和式（55） 代入，即得

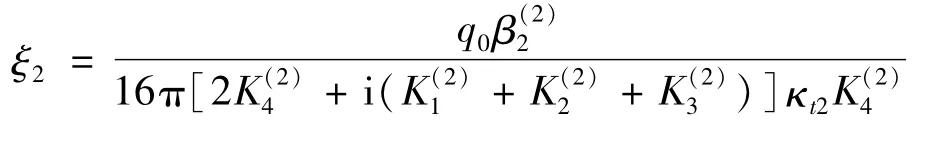
运用推广的Schwarz镜像延拓方法，在S+内定义Γ2（z） 的延拓函数

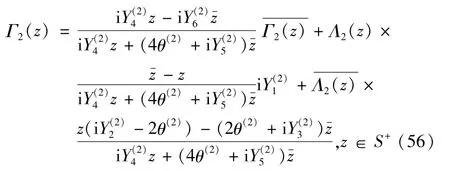
这样，Γ2（z） 可经过圆弧L′解析到S+内。

把式（54） 和式（55） 代入式（56），即得

对式（57）进行主部分析，可得到

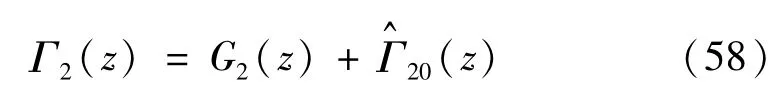
同样在S-内引入一函数

考虑边界条件式（2），并把式（56）和式（60）代入，在整个圆周L+L′上成立

由广义Liouville定理可得

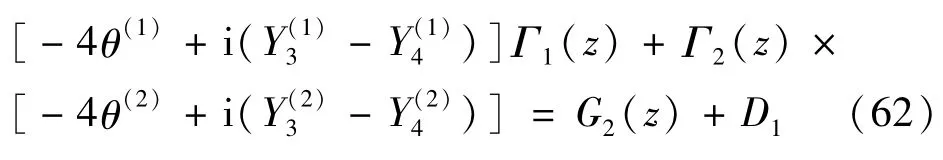
式中，D1为常数。

利用边界条件式（1），由式（58） 和式（62） 可得

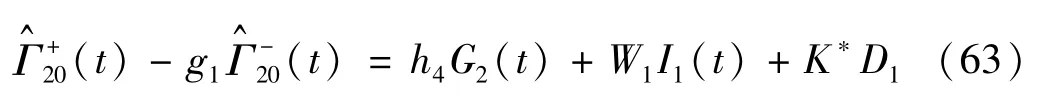
式中，g1，h4，W1，K*见附录A中式（A.3）。

式（63） 的解为

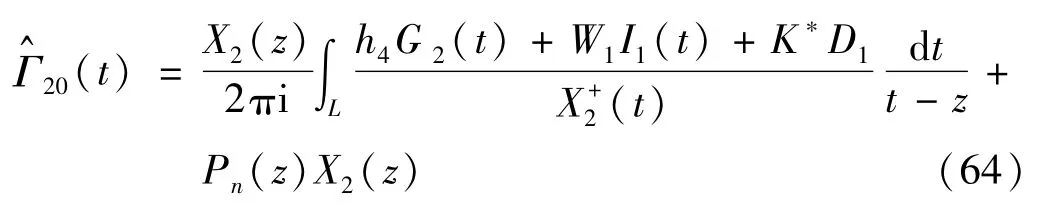
其中，

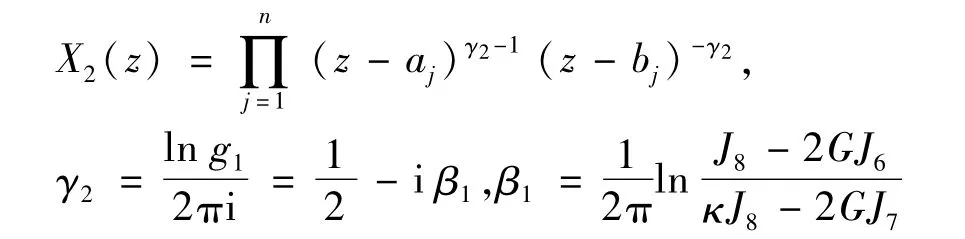
X2（z）是沿L割开平面上的任一单值分支，满足

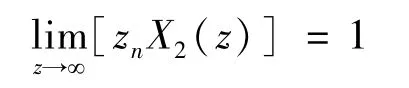
计算式（64） 的积分后，代入式（58） 和式（62），得Γ1（z），Γ2（z）。将 Γj（z） 的表达式代入式（56） 和式（60），即可求得

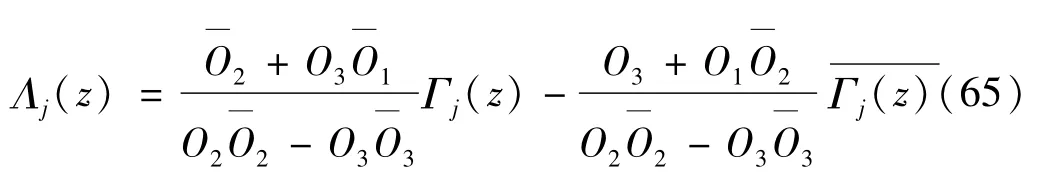
其中，

进而相位子场复势函数的表达式已求出。下面仍需确定c0，c1，c2，…，cn和D1，这n+2个常数。由无穷远处应力为0，得 Γ2（∞） =0，则由式（58） 和式（63） 可得:c0=0。

由于在无穷远邻域内

与式（58）在无穷远邻域的展开式比较系数，可得一方程，进而求得前的系数。

又考虑到 Γ1（∞）=D0，代入式（60） 得

由位移的连续性条件，考虑相对刚体位移，假设其中b1重合，则有n-1个独立条件，由此可得

把式（69）和式（73）代入上式，可得到n-1个方程，即

至此，全部常数已确定，从而相位子场的复势函数已求出。

5 典型问题

5.1 一条裂纹

如图2所示，考虑在准晶基体内任意一点z0作用强度为q0的点热源，在圆形夹杂界面上只含有一条裂纹b， 不失一般性，假设圆弧裂纹关于x轴对称，在圆形界面=R上有端点a=R e-iα，b=R eiα。

图2 含一条关于x轴对称的界面裂纹Fig.2 The case of an interface crack with respect to the x-axis symmetry

此时c0=0，n=1，由式（33） 可得

其中，

与式（20）比较系数得c1=0，因此

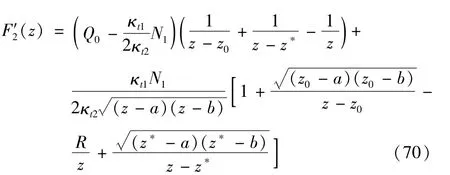
对式（71） 和式（72） 积分可得F1（z），F2（z），解析表达式见附录B中式（B.1）。

将上述解答退化到无裂纹圆形夹杂，即α=0，a=b=R，由式（69） 和式（70） 得

本文的结果与Chao等的研究结果一致，验证了本文结果的有效性。

5.1.2 声子场热应力

当n=1，c1=0时，D0=0，c1=A2。由此可得

式中，G′0（z），G′z0（z），G′z*（z），G′∞（z） 分别为被积函数在z=0，z0，z*，∞点处的奇性主部，具体表示见附录B中式（B.2）。这样声子场复势函数中的待定常数都已求出，声子场热应力也可确定。

5.1.3 相位子场热应力分析

当n=1，c0=0时，D1=0，c1=δ2。此时

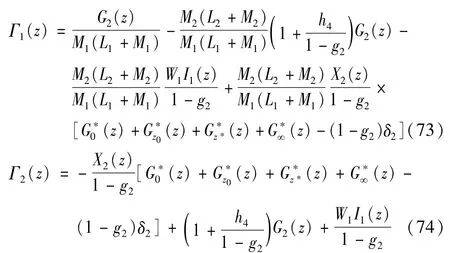
5.2 两条裂纹

如图3所示，考虑在准晶基体内任意一点z0作用着强度为q0的点热源，在圆形夹杂界面上含有两条裂纹不失一般性，假设两条圆弧裂纹分别关于x轴对称，在圆形界面=R上有端点a=R e-iα，b=R eiα，a′=R ei（π-α），b′=R ei（π+α）。

图3 含两条界面裂纹Fig.3 The case of two interface crack

5.2.1 温度场

此时c0=0，n=2，由式（33） 得

与式（20）比较系数得c1=0，由式（35）得确定常数c2的方程

由留数定理得c2=N1。

式（75）可改写为

把式（76） 代入式（34），得

对式（71） 和式（72） 积分可得F1（z），F2（z），解析表达式见附录C中式（C.1）。

将上述解答退化到无裂纹圆形夹杂，即α=0，a=b=R，按照这个过程，通过比较本文解与文献[21]解得一致性，验证了本文结果的有效性。

5.2.2 声子场热应力

当n=2，c1=0时，D0=0，考虑式（50），比较Ω2（z） 在无穷远展开的的系数，即得c1=A2，由式（53）得确定常数c2的方程

式中，G′0（z），G′z0（z），G′z*（z），G′∞（z） 分别为被积函数在z=0，z0，z*，∞点处的奇性主部，具体表示见附录C中式（C.2）。

5.2.3 相位子场热应力分析

当n=2，c0=0时，D1=0，此时

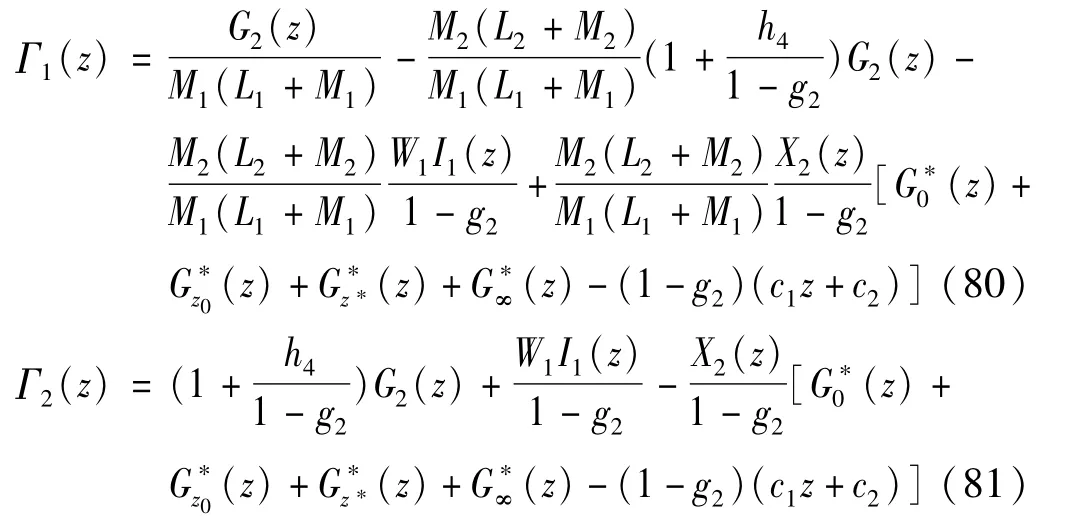
至此，相位子场的复势函数已确定。

5.3 裂纹尖端热应力强度因子

由于对称性，我们只考虑一条裂纹中一个裂纹尖端的热应力强度因子。为了计算圆弧裂纹端b点的热应力强度因子，首先做如下坐标变化

这样在Z平面X轴与裂纹相切与端点 （Z平面），且

在b1点领域的奇性主项可写为

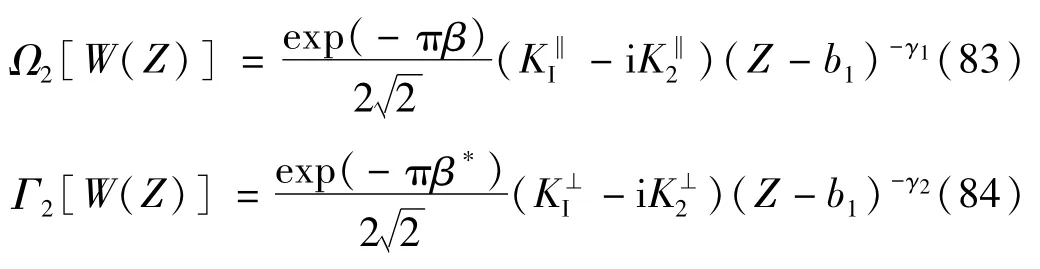
从式（85）和式（86）中可以看出，裂纹尖端的声子场和相位子场热应力强度因子与夹杂的半径以及热源的强度有关。

6 数值结果

本文利用复变函数方法研究了十二次二维准晶圆形弧段界面多裂纹的热应力问题，分别给出了热应力和裂纹尖端应力强度因子的解析解。利用此结果，求得一条裂纹，两条裂纹时热应力和裂尖应力强度因子的解析解。通过与现有结果的比对，可以验证本文所得结论的正确性，同时也可以说明本文所研究的问题具有的普遍性。

取准晶夹杂、基体的材料参数如表1所示。

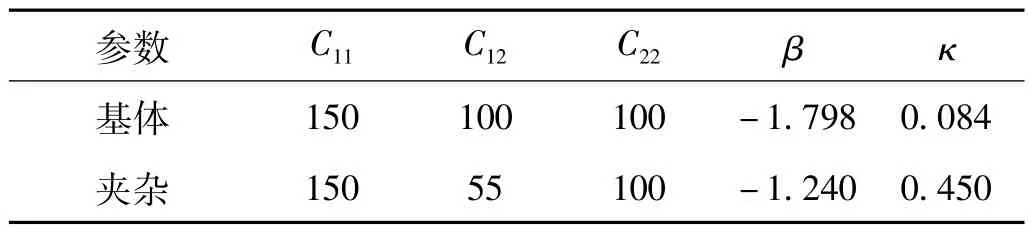
表1 十二次二维准晶材料参数Tab.1 Material parameter of dedecagonal two-dimensional quasicrystals

对应力和应力强度因子进行无量纲处理

图4和图5给出了含一条裂纹时，不同强度点热源作用下，无量纲场热应力随极坐标转换角度θ的变化关系。结果表明，随着热源强度的增大，热应力增大，并且在θ=45°和θ=315°附近热应力集中。图6和图7给出了含两条裂纹时，不同强度点热源作用下，无量纲场热应力随极坐标转换角度θ的变化关系。结果表明，随着热源强度的增大，热应力增大，两者呈线性关系。并且在θ=30°，θ=150°，θ=210°和θ=330°附近热应力集中。

图4 不同q0时边界上的径向应力σr0，α=45°Fig.4 The nondimensional radial stressσr0 for different q0，α=45°

图5 不同q0时边界上的切向应力 σrθ0，α=45°Fig.5 The nondimensional shear stressσrθ0 for different q0，α=45°

图6 不同q0时边界上的径向应力σr0，α=30°Fig.6 The nondimensional radial stressσr0 for different q0，α=30°

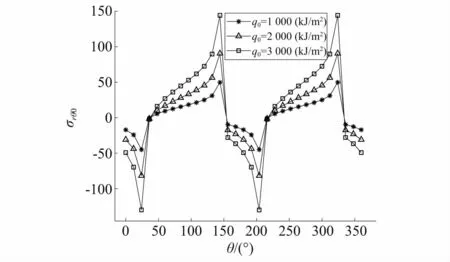
图7 不同q0时边界上的切向应力 σrθ0，α=30°Fig.7 The nondimensional shear stressσrθ0 for different q0，α=30°

根据式（82）的定义，引入应力强度因子来分析裂纹尖端热应力的变化。图8和图9显示了不同夹杂半径下，无量纲热应力强度因子K10及K20随裂纹角度α的变化关系。从图8可以看出，无量纲热应力强度因子K10随着裂纹角度α的增大而变大，从图9可以看出，无量纲热应力强度因子K20随着裂纹角度α的增大先减小，在α=45°附近达到最小值，然后随之增大。因此在实际工程中可以适当调整夹杂半径来降低裂纹尖端的集中。

图8 不同R时K10随裂纹角度α的变化Fig.8 Change of the nondimensional K10 with crack angle for different R

图9 不同R时K20随裂纹角度α的变化Fig.9 Change of the nondimensional K20 with crack angle for different R

图10和图11显示了点热源强度不同时，无量纲热应力强度因子K10及K20随裂纹角度α的变化关系。可以观察到热源强度不会影响热应力强度因子的变化趋势，但会影响到热应力强度的大小，并且热源强度越大热应力强度因子越大。从图10可以看出，无量纲热应力强度因子K10随着裂纹角度α的增大而变大，从图11可以看出，无量纲热应力强度因子K20随着裂纹角度α的增大先减小，在α=40°附近达到最小值，然后随之增大。

图10 不同q0时K10随裂纹角度α的变化Fig.10 Change of the nondimensional K10 with crack angle for different q0

图11 不同q0时K20随裂纹角度α的变化Fig.11 Change of the nondimensional K20 with crack angle for different q0

7 结 论

利用Muskhelishvilv复变函数方法，通过复应力函数奇性主部分析和Riemann-Schwarz解析延拓原理法，获得了在集中热源作用下，不同材料界面裂纹热弹性问题的温度场和弹性场的一般解答，分别求出了含一条和两条界面裂纹时热应力的解析表达式，并以图表的形式讨论了不同准晶复合材料随裂纹几何条件变化对裂纹尖端热应力强度因子的影响规律。结果显示在点热源作用下含界面裂纹圆形夹杂的裂纹尖端具有应力振荡奇异性。本文的结果可作为若干实际问题的力学模型，为准晶材料的细观结构设计以及界面破坏机理提供了科学依据。

附录A

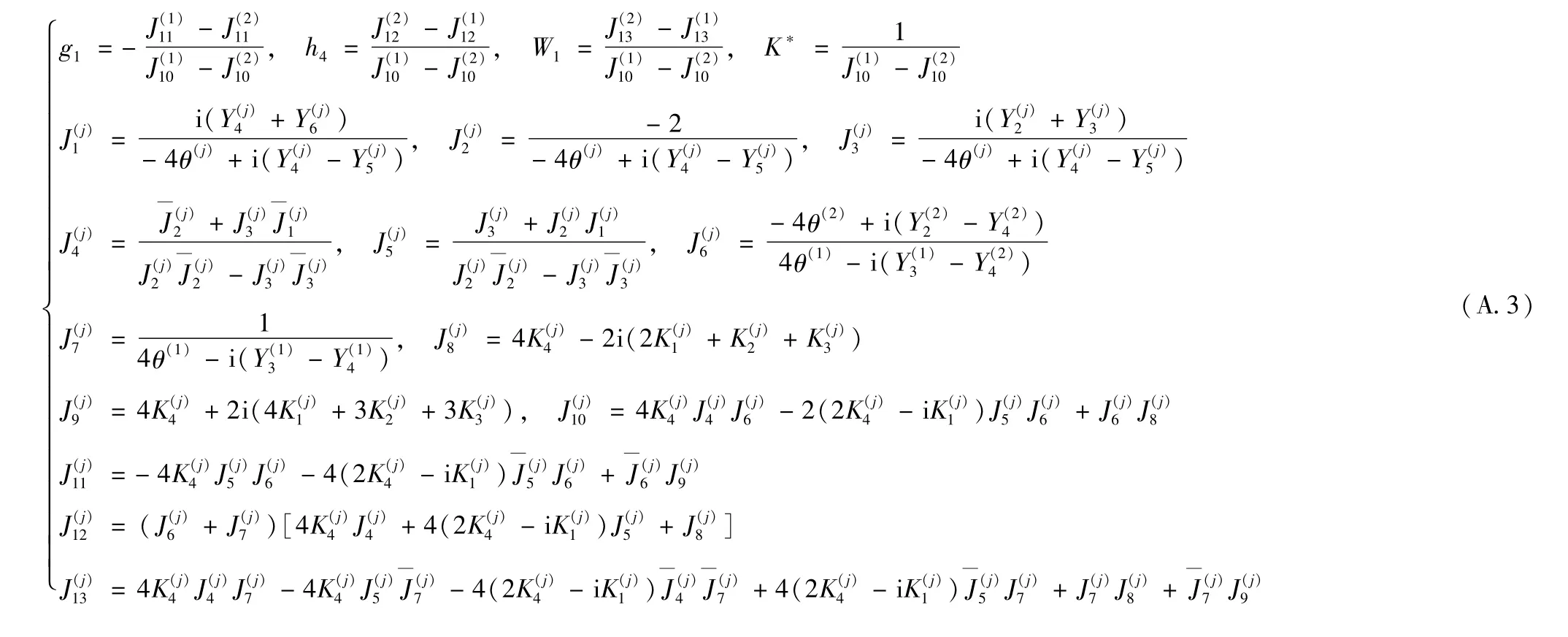
附录B

附录C