基于层间分离的玻璃钢夹砂管渐进损伤仿真与强度计算

王清洲，孙言文，肖成志，魏连雨

（河北工业大学 土木与交通学院，天津 300400）

玻璃钢夹砂管作为一种新型复合材料柔性管涵，是由树脂、纤维、石英砂缠绕而成的多层复合结构，具有高比强度、高比模量、优异的耐腐蚀性等优点，广泛应用于石油、化工和市政给排水等工程中[1]，近年来逐渐应用于公路排水工程中。然而，目前公路行业涉及多层玻璃钢夹砂管的强度计算和结构设计远落后于工程实践。由于在玻璃钢管道中引入石英夹砂层，所形成的多个夹砂层-树脂纤维层层间界面成为管涵结构受力的薄弱环节，服役期内，埋地玻璃钢夹砂管涵承受压缩和弯曲的耦合作用，层间分离是该受力状态下最常见的失效破坏形式[2]。以往针对玻璃钢夹砂管数值模拟和失效机理的大量研究只考虑了基体开裂、纤维断裂、单层板完全失效及材料退化的渐进损伤过程，由于未考虑结构层层间分离的失效模式[3-4]，使设计出来的玻璃钢夹砂管涵强度偏于保守造成生产成本浪费。因此，考虑层间分离失效模式，开展受压管涵强度预测和力学行为研究具有重要的工程意义。

荷载作用下夹砂管涵破坏是一种极其复杂的物理现象。由于存在多个层间界面，各层材料性能和厚度值迥异，并且多种损伤模式之间彼此诱发和相互耦合，极易引发层与层之间产生不连续的应力突变[5-7]，尤其是在层间黏合不均匀区域应力集中更易发生，使夹砂管涵结构的力学行为和强度预测更复杂[8]。虽然数值模拟技术已经广泛应用于玻璃钢夹砂管道力学分析、破坏机理推演以及管道优化设计等方面，尤其能够考虑层间分离和材料渐进失效等复杂情形实现从初始加载到破坏全过程的仿真，但其仿真精度的提高是难点问题[9]。数值计算方法精度提高的关键在于选取合适的强度准则和材料退化模型来与实际破坏过程相吻合。绝大多数研究中玻璃钢夹砂管强度预测模型采用Hashin失效判据[10]和Camanho[11]提出的刚度退化准则以及Rafiee[12]针对玻璃钢夹砂管道受力特性专门提出的破坏准则，忽略了层间分离这一破坏模式，使强度预测误差较大。管壁结构型式和厚度是玻璃钢夹砂管涵设计的重要物理参数，决定着管涵强度等力学性能和失效机制[13]，然而，目前针对缠绕层与夹砂层共存的特殊多层玻璃钢夹砂管涵结构型式，鲜有关于管壁结构层数和层厚与管涵力学性能和失效机制相关研究的报告，亟待建立基于层间界面失效模式的玻璃钢夹砂管渐进损伤模型，发展模型合理简化、计算精度高的有限元强度分析方法。

为此，本文利用有限元ABAQUS软件编写UMAT子程序实现管涵层间损伤的渐进失效计算模型，以此开展夹砂管涵失效机理和损伤演化全过程仿真，建立玻璃钢夹砂管涵的损伤演变过程与其宏观可测力学性能变化之间的关系，通过广泛的参数分析阐明荷载作用下管涵结构力学行为和内部损伤动态扩展规律，实现管涵结构型式和参数的优化。

1 层合板渐进失效模型

1.1 单层板失效准则

单层板是复合结构的基本单元，包括缠绕层和夹砂层，它在承载时是否失效是复合材料是否损伤判断依据。从复合材料细观力学计算角度将缠绕层和夹砂层看作材料属性不同的单层板，在承受恒荷载、可变荷载、偶然荷载等不同荷载的冲击时，由于应力分量的作用，会出现多种损伤形式，选用最大应力准则作为夹砂层的失效判定准则、Hashin强度准则作为缠绕层的失效判定准则。

1.1.1 缠绕层失效判据

缠绕层的破坏形式主要有纤维拉伸破坏、纤维屈曲、基体拉伸开裂、基体压缩开裂等破坏形式，当材料满足任何一种失效指标时则认为发生失效。Hashin失效准则[14]可以计算不同方向应力之间的耦合效应，判据公式简单，在工程制造领域中广泛用于复合材料强度的计算，并经工程实践检验具有较可靠的计算精度，其准则表达式[15]为

纤维拉伸断裂失效

纤维压缩断裂失效

基体拉伸或剪切失效

基体压缩或剪切失效

式中:σ1为缠绕层1方向的拉伸应力；σ2为缠绕层2方向的拉伸应力；τ12为缠绕层1-2方向的剪切应力；Xt为单层板纵向拉伸强度；Xc为单层板纵向压缩强度；Yt为单层板横向拉伸强度；Yc为单层板横向压缩强度；S12为单层板1-2方向的剪切强度。

1.1.2 夹砂层失效判据

为满足埋地管涵高强度与高刚度的要求，采用掺入较厚夹砂层的方式来增强管涵整体刚度。由树脂和石英砂构成的夹砂层具有各向同性的特点，某个应力分量达到夹砂层材料的极限强度值作为单层板最终破坏的标准，即最大应力强度准则，主要通过将失效夹砂层的力学性能（杨氏模量和泊松比）降低至零来实现，从而避免有限元分析中的数值不稳定。夹砂层纵向压缩失效、纵向拉伸失效、横向压缩失效、横向拉伸失效、剪切失效时的判定公式分别为

式中:σ′1为夹砂层1方向的拉伸应力；σ′2为夹砂层2方向的拉伸应力；τ′12为夹砂层1-2方向的剪切应力；X′t为夹砂层纵向拉伸强度；X′c为夹砂层纵向压缩强度；Y′t为夹砂层横向拉伸强度；Y′c为夹砂层横向压缩强度；S为夹砂层的剪切强度。

1.2 单层板刚度退化准则

损伤演化的特征是材料刚度的渐进退化，在损坏开始之前，复合材料处于线性弹性阶段，其应力-应变的关系为

式中:σ为复合材料的应力矩阵；ε为复合材料的应变矩阵；C为损伤变量的刚度矩阵。

当单层板发生基体开裂或剪切破坏时，损伤演化开始，在识别损伤开始之后，通过进一步施加荷载，失效的层合板力学性能不断降低，复合材料的刚度开始逐渐退化。当单层板满足失效判据后，引入损伤变量刚度矩阵表征其性能退化[16]，如式（7）所示。

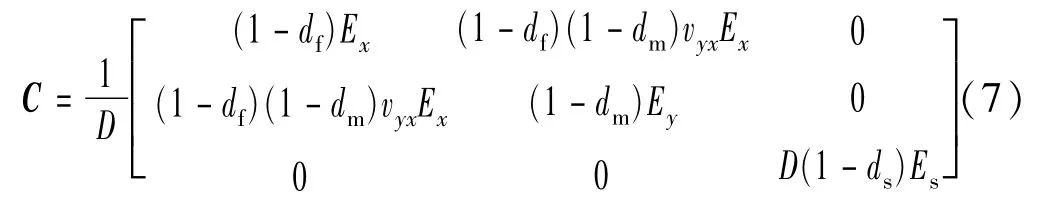
式中:D反映了当前损伤状态，D=1-（1-df）（1-dm）×vxyvyx＞0；df，dm，ds分别为纤维破坏、基体破坏和剪切破坏的状态，表示为

每个损伤变量在特定模式下的增长与使用下列表达式计算等效位移有关

式中:σI，eq为失效开始时的失效位移，计算公式为

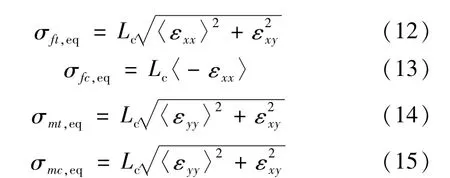
1.3 分层失效判据

为模拟夹砂管涵层间分离的破坏形式，采用基于表面的黏聚行为来定义层间关系从而实现层间分离的有效模拟。采用cohesive单元和基于traction-separation描述的方法进行模拟，选用双线性本构模型[17-18]作为控制方程，如图1所示。图1表征了材料达到强度极限前的线弹性段和材料达到极限强度后的刚度线性降低演化阶段。

图1 双线性黏附力-位移示意图Fig.1 Schematic diagram of bilinear adhesion displacement

三维模型中名义黏聚力矢量由三个分量组成:Tn为法向，Ts和Tt为剪切方向，在开始分层之前，黏聚力和分离力之间的关系由式（17）表示

初始损伤对应于材料开始退化，当应力或应变满足于定义的初始临界损伤准则时退化开始，玻璃钢夹砂管涵建模中选用quads damage二次名义应力准则[19]，当各个方向的名义应变比的平方和等于1时损伤开始[20]表征为

单元损伤演化采用基于能量的损伤演化规律，刚度退化方式选用线性演化模型，混合模式选择B-K准则[21]用以反映材料在复杂应力状态下的断裂能量释放率，表达式为

式中:Gn，Gs，Gt分别为三个方向的断裂韧性；η为B-K指数。

1.4 层合板渐进失效分析过程

多层玻璃钢夹砂管管壁结构的损伤过程是一个复杂的非线性逐层失效过程，要经历损伤及层间分层、材料性能退化、结构失效等阶段，利用ABAQUS有限元软件建模，采用选定的失效准则和刚度退化准则建立玻璃钢夹砂管涵渐进失效的强度计算模型，计算流程如图2所示。

图2 层合板渐进失效模型流程图Fig.2 Flow chart of progressive failure model of laminated plates

2 渐进失效模型验证

2.1 试验材料及方法

选取内径为1 500 mm、壁厚为50 mm、宽度为300 mm的玻璃钢夹砂管环，缠绕层由交叉缠绕和环向缠绕组成，环向缠绕的缠绕角度为90°，层厚为0.4 mm，交叉缠绕是由缠绕机螺旋缠绕成型，交叉缠绕层由一组正负57.46°对称缠绕层形成，层厚为0.8 mm。夹砂层由不饱和聚酯树脂和石英砂混合成型，经离心转动和压实而成。管涵的铺设结构如图3所示，各层材料如表1所示。

表1 各层材料构成Tab.1 Material composition of each layer

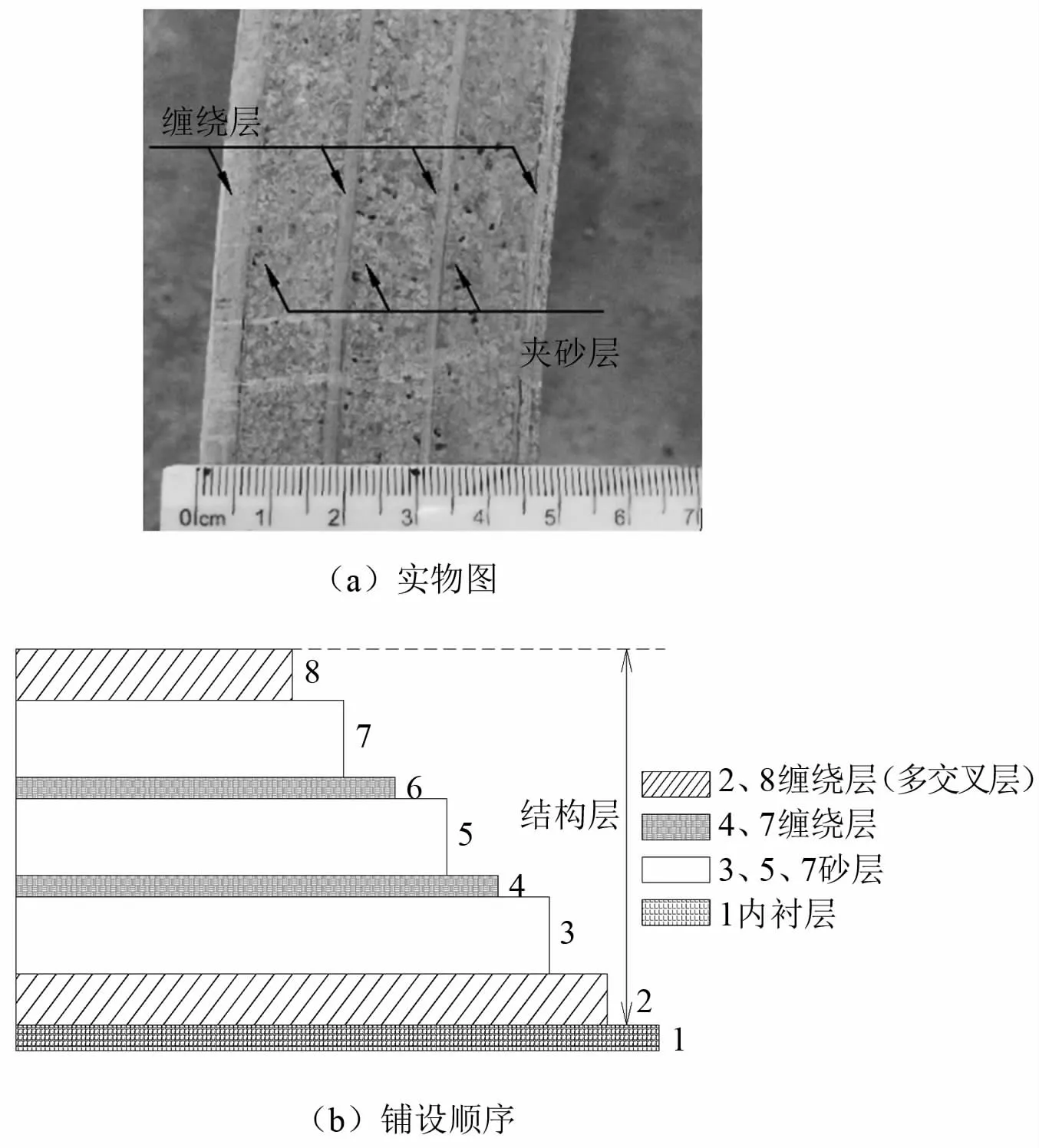
图3 管涵铺设结构图Fig.3 Pipe culvert laying structure drawing

管涵静载破坏试验采用平行板外载施压试验方法加载，参照GB/T 21238—2007《玻璃纤维增强塑料夹砂管》中的试验方法及要求，将管环持续加载直至破坏，得到层间分离时荷载为68.41 kN，夹砂层失效时荷载为76.21 kN，极限破坏荷载为81.4 kN，破坏试验如图4所示。

图4 试验管环的加载图Fig.4 Loading diagram of test pipe ring

2.2 材料力学性能

生产夹砂管涵的纤维、树脂、石英砂等组成材料的质量分数和力学参数，如表2所示。表2中材料的力学参数由供应商提供，质量分数由“光-色-热-质-元-化”联用技术的成分分析试验得到，单层板弹性力学参数根据文献[22-23]中的公式计算得到，列于表3。

表2 缠绕层原材料的力学性能Tab.2 Mechanical properties of raw materials for windinglayer

表3 力学参数计算值Tab.3 Calculated values of mechanical parameters

2.3 渐进失效模型建立

建立长度为300 mm的可变形拉伸实体模型，选用上下均为300 mm×300 mm的刚性加载板，建立discrete rigid的模型，如图5所示。加载时对上下两块刚性平行板设置对应参考点RP1和RP2，刚性板与试验管涵之间设置为绑定约束。根据平行板试验要求，对RP2点施加三个方向的位移约束和转动约束，用以固定下加载板；对RP1点施加沿Y轴负方向速度为10 mm/min的位移荷载，并对其他方向进行约束，实现通过上加载板产生位移来加载的目的。为消除传统玻璃钢夹砂管建模时未考虑层间分离破坏模式的局限性，引入基于双线性本构模型和B-K断裂能损伤演化准则的内聚力表面（surface-based cohesive）建模法模拟管涵受压时所产生的层间分离，相邻层之间的黏附性采用零厚度界面的相互作用来定义，建立黏附力矢量与层间分离状态之间的相关性。模型中，每一层被定义为具有不同厚度的独立圆柱，每层的内径被认为与前一层的外径相同，对夹砂层采用结构式划分网格技术，对玻璃钢缠绕层采用扫掠式网格划分技术，扫掠方向定义为沿单层板厚度方向。通过设置黏结面组合在一起，由于每个层都是独立建模的，因此可以在相邻层的界面中正确定义基于表面的内聚行为。黏结面的性能和参数取值列于表4中[24]。编写了UMAT子程序以实现Rafiree刚度退化准则与渐进失效过程，得到玻璃钢夹砂管渐进失效计算模型。

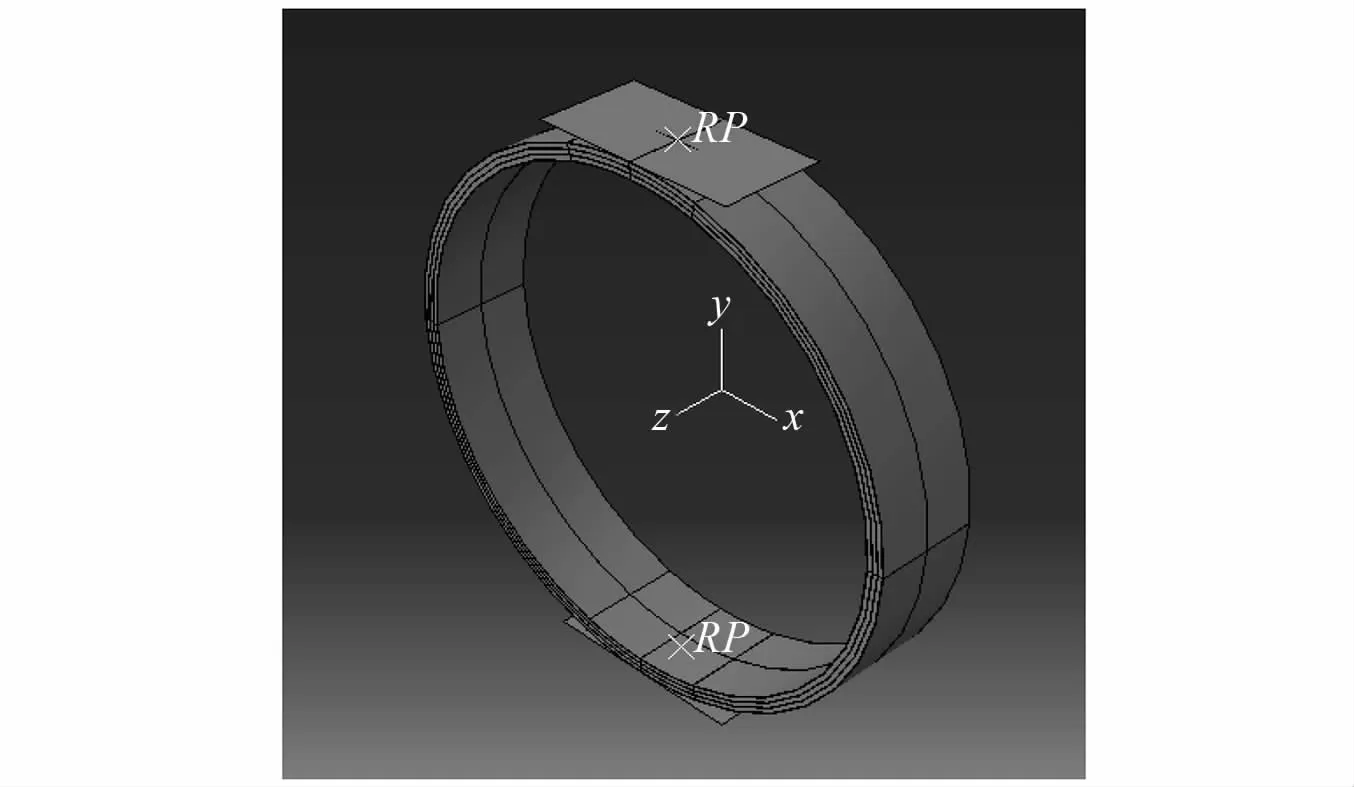
图5 模型外形尺寸和受力方式Fig.5 Overall dimension and stress mode of the model

表4 界面黏结性能Tab.4 Interface bonding performance

2.4 极限强度验证

经管样最大破坏荷载的模拟值与实验值进行对比，列于表5，荷载-位移曲线如图6所示。

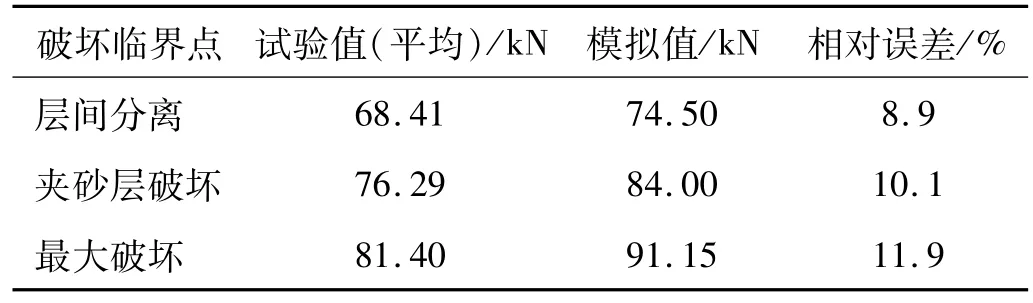
表5 管涵破坏临界点荷载模拟值与试验值对比Tab.5 Comparison of simulated and experimental load at critical failure point of pipe culvert

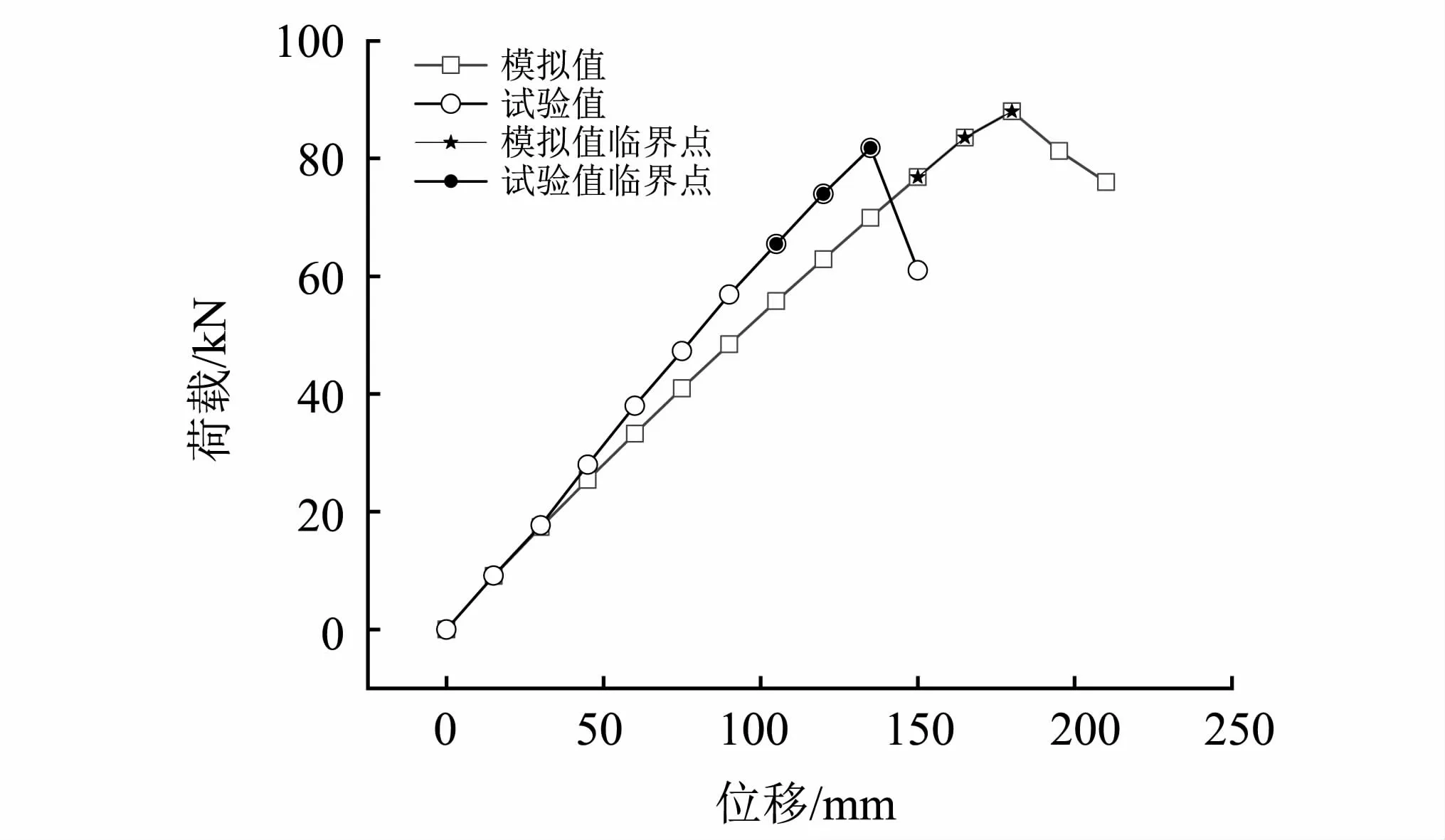
图6 试验值与模拟值的对比Fig.6 Comparison between test value and simulation value

图6中可以看出，荷载-位移曲线的总体变化趋势一致，试验值略小于模拟值。层间分离破坏临界点的荷载模拟值和实验值相差6.09 kN，相对误差为8.9%，夹砂层破坏临界点的荷载值相差7.71 kN，相对误差为10.1%，最大破坏点的荷载值相差9.7 kN，相对误差为11.9%，均在工程实际可以接受的范围之内，误差的主要来源于对材料性能和结构的理想化假设。

3 结果与分析

3.1 管涵渐进失效破坏历程

由管涵破坏试验可知，管涵失效的历程主要经历:裂缝出现及发展、层间分离、夹砂层破坏、缠绕层破坏（最大破坏荷载）、管涵屈服失效五个阶段，其中层间分离、夹砂层破坏、缠绕层破坏为三个典型的破坏临界点。荷载作用下，裂缝首先多出现在外侧夹砂层的上下表面以及中间砂层的上表面等砂层结构的薄弱位置，细小且无规律分布；随后，裂缝逐渐发展，不同砂层的个别裂缝快速变长、变宽引发层间分离破坏，此时应力重分布，随着持续加荷直至裂缝贯穿整个夹砂层而产生剪切破坏；随着1～2层的夹砂层失效，部分完好的夹砂层和缠绕层共同受力，荷载增大速度变缓，整个管涵变形量迅速增加，直至缠绕层发生破坏，管涵进入屈服失效阶段。数值模拟方法能够重现管涵破坏的这一历程，但裂缝总是首先出现在外侧夹砂层的上下表面，随着荷载增加外侧砂层表面先发生层间分层并伴随着其他砂层的层间裂缝出现和快速发展，主要原因为管壁结构的外侧受力较内侧要大。模拟结果与试验结果的主要差异在于，管壁结构均匀的理想状态下中间砂层受力很小，直到管涵发生屈服破坏时其受力值也未达到剪切破坏的极限值，这一现象与实际由于管壁结构和材料变异性很大，外侧层间分离后发生应力重分布，中间砂层也容易发生破坏的现象不相符。模拟结果表明，管样各层破坏程度相差较大，并且内层变形比外层更加明显，甚至在管涵顶部和底部出现反向屈曲现象，说明管样在沿厚度方向的应力响应并不是线性变化的。提取各层的应力云图可以发现各层应力分布各有不同，这是由于每一层的材料类型、厚度、铺层方式、缠绕角度不同所导致，从而导致在受到外部压荷载时各层内部应力响应差异较大。因此，服役中的玻璃钢夹砂管涵如果存在层间黏合力较差，则极易发生层间剪切破坏。整个破坏过程至少2层以上砂层和一层缠绕层完全破坏，最终管涵出现屈曲失稳破坏，并非所有结构层全部破坏的终层失效模式。数值模拟管涵破坏过程的云图，如图7所示。

图7 管涵破坏过程重要临界点的数值模拟示意图Fig.7 Numerical simulation diagram of critical points in the failure process of pipe culvert

3.2 夹砂层厚度对管涵破坏的影响规律

选取8 mm，10 mm，12 mm，14 mm四个不同的夹砂层厚度进行平行板加载破坏仿真来研究夹砂层厚度对管涵破坏的影响规律，提取层间分离、夹砂层破坏、缠绕层破坏三个临界点对应的荷载值和变形值列于表6，建立荷载值随夹砂层厚度的变化趋势，如图8所示。

图8 各破坏临界点荷载值和位移随夹砂层厚度的变化趋势Fig.8 Variation trend of load value and displacement of each failure critical point with sand layer thickness

表6 不同厚度夹砂层对应的各破坏临界点的荷载值Tab.6 Load values of each failure critical point corresponding to different thickness of sand layer

表6和图8说明，随着夹砂层单层厚度由8 mm增加至14 mm，管涵的最大破坏荷载值增加了117%，管样破坏时的变形值减小了37%；单层夹砂层厚度8 mm的管样破坏时的变形最大，可达到管径D的18.8%，三个破坏临界点的荷载值较为接近，管涵的失效历程所持续时间较短，即层间分离状态很接近管涵的最终失效状态。14 mm砂层厚度对应的荷载值的增幅大于其他厚度荷载值的增幅，随着夹砂层厚度的增加，三个临界点荷载值的差距逐渐变大，从层间分离到夹砂层完全剪切破坏需要经历一个相对较长的加载过程，同时各临界点对应的荷载值随厚度增大而变大，但发生破坏时的变形值则逐渐降低，表明管涵最大破坏荷载和刚度随着夹砂层厚度的增大而增大，管涵柔韧性和变形量随着夹砂层厚度增加而逐渐减小。因此，管涵设计时可通过调整夹砂层厚度来满足管涵不同承载能力和刚度的需要。

3.3 夹砂层层数对管涵破坏的影响规律

选取二层和三层夹砂层管壁结构作为研究对象，研究夹砂层层数对管涵强度的影响规律。二层夹砂管壁结构为三层夹砂结构中去掉一层夹砂层和一层缠绕层，并将去掉的两层厚度一分为二增加至每一个单层夹砂层中，使管壁保持总厚度不变。二层夹砂管壁结构示意图如图9所示，对应21.6 mm，18.6 mm，15.6 mm，12.6 mm四种单层夹砂层的厚度，计算结果列于表7中，二层和三层夹砂结构的各破坏临界点对应荷载值的对比见图10和图11。

图9 二层管涵结构各层示意图Fig.9 Schematic diagram of each layer of pipe culvert structure on the second floor

表7 不同单层厚度二层夹砂结构对应各临界点的荷载值和位移值Tab.7 Load value and displacement value of each critical point corresponding to two-layer sand sandwiched structure with different single layer thickness

表7和图10和图11显示，二层夹砂管壁结构随着单层夹砂层厚度由12.6 mm增加到21.6 mm，管涵的最大破坏荷载值由42.94 kN增大至103.22 k N增加了140%，管样破坏时的变形值由283.99 mm减小至205.33 mm，减小了28%，单层夹砂层厚度12.6 mm的管样破坏时的变形最大，可达到管径D的18.9%。管壁总厚度相等的二层夹砂结构破坏过程变化规律与三层夹砂结构一致，各单层厚度对应的破坏临界点荷载值显著高于三层夹砂结构的荷载值，实际工程应用中选用含两层夹砂管壁结构所能承受的破坏荷载更大，优于三层夹砂层的管壁结构。

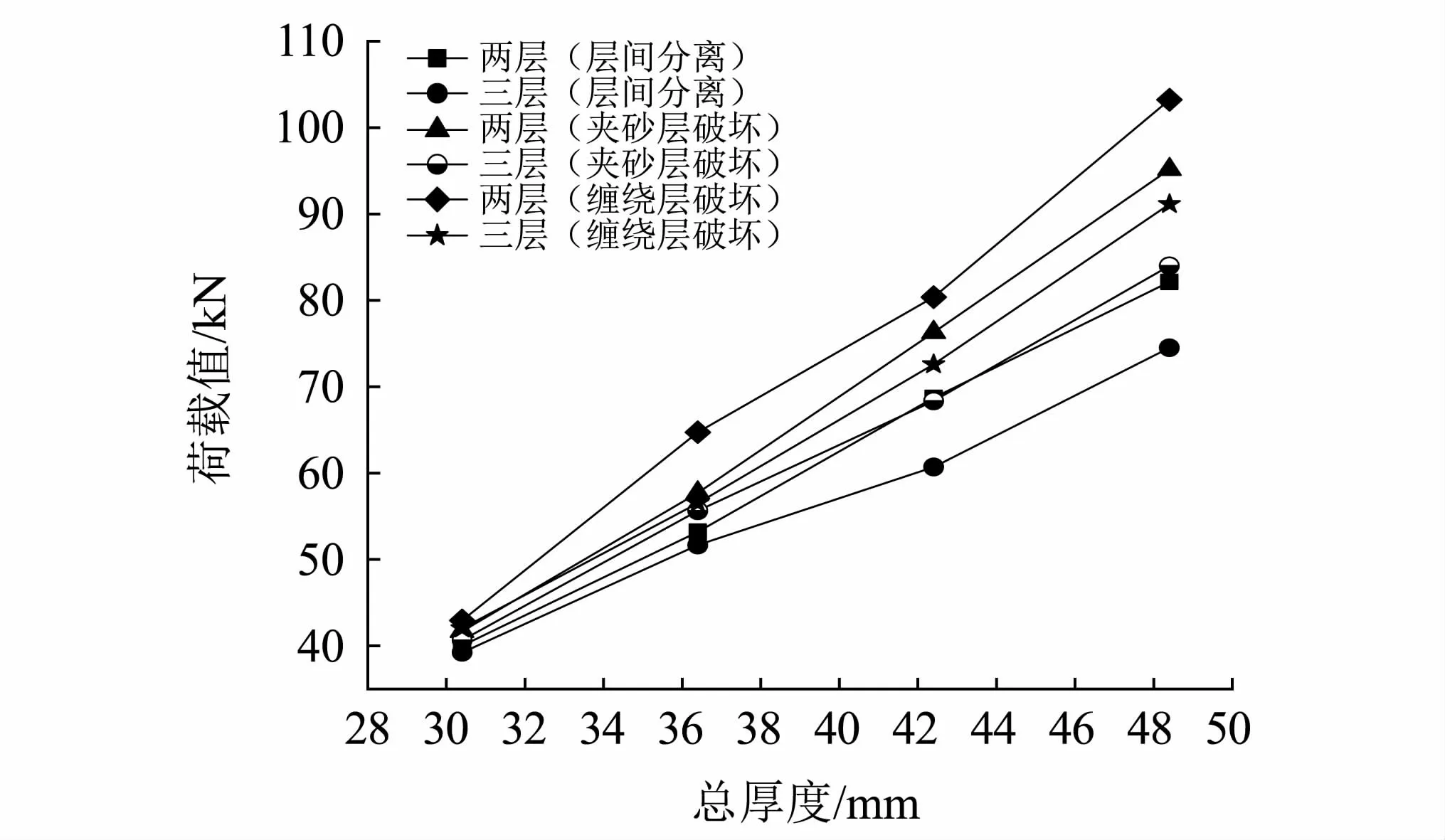
图10 不同夹砂层层数管涵结构各破坏临界点荷载值对比Fig.10 Comparison of load values at critical failure points of pipe culvert structures with different sand layers

图11 不同夹砂层层数管涵结构各破坏临界点位移值对比Fig.11 Comparison of displacement values at critical failure points of pipe culvert structures with different sand layers

3.4 破坏过程中各结构层应力变化规律

为研究管涵结构破坏过程以及各结构层的受力破坏状态，提取管壁结构各自每一结构层（缠绕层和夹砂层）加载至破坏荷载全过程中的应力值，分析管壁结构压荷载作用下的受力规律。选取缠绕层和夹砂层沿壁厚方向位于加载板的中心位置作为应力提取点，图12为各缠绕层和夹砂层的应力提取点，绘制各结构层应力随荷载变化的趋势如图13和图14所示。

图12 各结构层的应力提取位置示意图Fig.12 Schematic diagram of stress extraction location of each structural layer

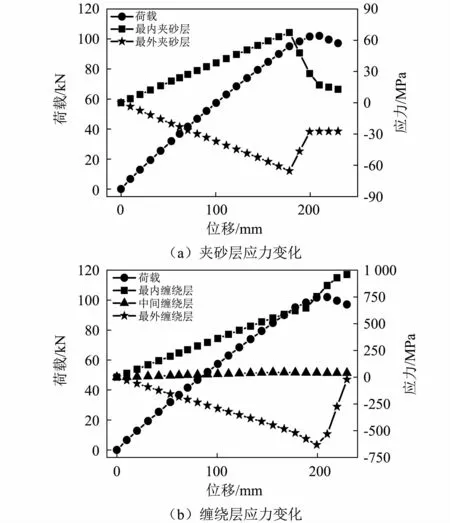
图14 二层夹砂结构各层应力随加荷位移变化的趋势图Fig.14 Variation trend of stress of each layer of two-layer sand sandwiched structure with load displacement

由图13可知，荷载作用下三层夹砂结构的夹砂层和缠绕层受力均随荷载呈线性增加，内外层所受应力关于壁厚中心呈拉压相反状态，力值大小基本相等，而中间夹砂层在整个过程中的受力几乎为零。当竖向加载位移达到150 mm时，最外层和最内层夹砂层发生破坏，此时缠绕层为主要受力层，应力重新分布，管涵结构的整体抗压性能下降，随后缠绕层材料性能开始退化。当达到最大破坏荷载91 kN时，最外缠绕层发生破坏，所受压应力达到613 MPa，最内缠绕层拉应力达到743 MPa，由于纤维抗拉强度远大于抗压强度，所受压应力的最外层缠绕层最先破坏。达到极限破坏荷载后，三层夹砂结构管涵虽中间夹砂层和三层缠绕层未全部破坏，但管涵结构进入塑性变形阶段，变形显著增加而荷载显著下降，管涵已屈服无法继续承受压荷载。

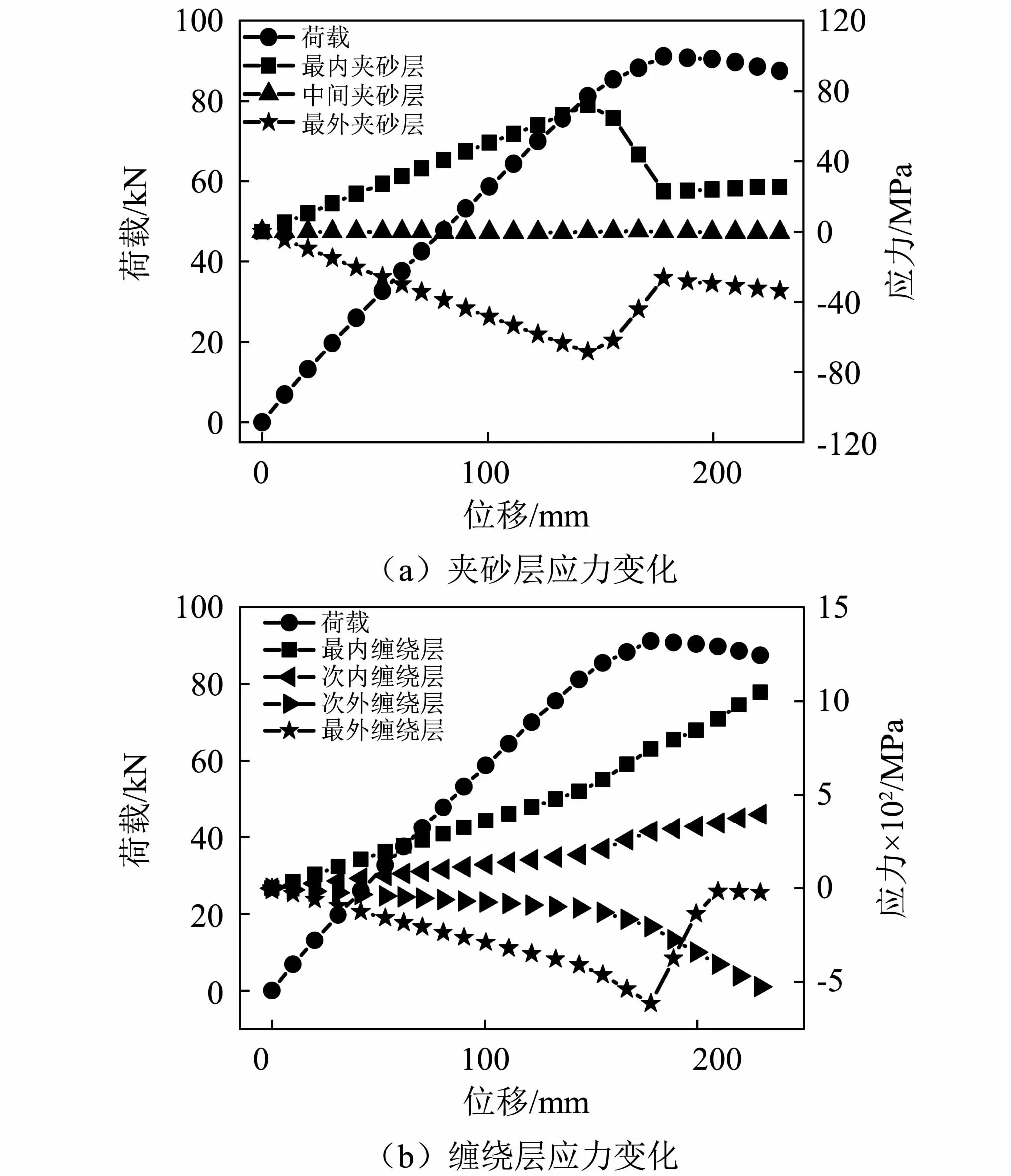
图13 三层夹砂结构各结构层应力随加荷位移变化的趋势图Fig.13 Variation trend of stress of each structural layer of three-layer sand sandwiched structure with load displacement

由图14可知，二层夹砂结构最大破坏荷载为103 kN，外缠绕层发生破坏，最大压应力为631 MPa，而此时内缠绕层的最大拉应力达到753 MPa仍未破坏，由于二层夹砂结构中夹砂层厚度相比三层夹砂结构要厚，其夹砂层破坏对应的加荷位移为180 mm，高于三层夹砂层结构破坏时的150 mm位移。主要原因为二层夹砂层结构沿管壁厚度方向的中心为内缠绕层而不是中间砂层，虽然管壁结构总厚度相等，但二层夹砂层结构将三层结构中间整个破坏过程中受力几乎为零的14 mm砂层材料均分到每一个夹砂层上使单层厚度变厚，荷载作用下树脂砂在极限破坏状态下发生破坏，中间夹砂层的材料性能得到了充分利用，从而提高了管涵结构整体的最大破坏荷载值。因此，管壁结构设计时优先选用相等的偶数（大于0）砂层结构，保证充分发挥砂层材料性能。

4 结 论

（1）引入基于双线性本构模型和B-K断裂能损伤演化准则的内聚力表面建模法来模拟管涵层间分离，缠绕层单层失效判据采用Hashin破坏准则，夹砂层采用最大主应力失效判据，编写了UMAT子程序实现Rafiree刚度退化准则与渐进失效过程，提出了考虑层间分离的玻璃钢夹砂管涵渐进失效强度计算方法。

（2）数值计算结果表明，管涵破坏过程始终是先发生层间分层，继而是夹砂层破坏，最后是管样最终破坏，各阶段对应的荷载值和变形值均逐渐变大。砂层厚度增大对提高管涵刚度有利，单夹砂层厚度14 mm时，三个破坏阶段的荷载值的差距逐渐变大，从层间分离到夹砂层完全剪切破坏需要经历一个相对较长的加载过程，对于管涵而言储备了更多的延性破坏能力。

（3）夹砂层层数变化对玻璃钢夹砂管涵的破坏各阶段的荷载值和变形值影响较显著，管壁总厚度相等的偶数砂层结构的力学性能要优于奇数砂层结构，管壁中心的夹砂层材料的力学性能达到充分发挥。公路用玻璃钢夹砂管涵洞管壁结构建议采用偶数夹砂层数对称设计，单层夹砂层厚度尽量取大值。