基于履带环影响和功率谱方法的履带车辆振动响应分析

乔新勇，靳 莹，段 誉

（陆军装甲兵学院 车辆工程系，北京 100072）

由于履带对车辆振动的影响，使履带车辆在越野路面上行驶时的振动响应与轮式车辆有很大的区别。建立准确的履带车辆动力学模型以及振动响应分析方法是研究车辆振动响应的重要技术手段[1-4]。考虑到履带对车辆振动特性影响的复杂性，如何在履带车辆动力学模型中准确的描述履带的振动特性是确保模型精度的关键。丁法乾[5]从理论上定性描述了履带对车辆振动的影响，但在后续建模中仍忽略了履带作用。Campanelli[6]采用坐标简化法将履带环划分为不同区间建立履带的运动学方程，分析了履带车辆的振动特性，但未对履带环的影响进行分析。史力晨等[7]在建立履带车辆数学模型时，将履带对负重轮的约束力添加到负重轮的集中质量上，但未考虑履带环的几何约束。Scholar等[8]提出基于连续弹性体履带的履带车辆系统模型，为分析履带的振动提供了参考。Han等[9]基于DADS软件分别建立了采用刚性履带和柔性履带的履带车辆模型，并开展了车辆行驶平顺性的对比研究。孟磊等[10]采用LMS软件建立了考虑刚性履带的底盘系统模型和未考虑履带的履带车辆台架试验模型，并基于两种模型计算了履带车辆振动响应的差异。黄晋英等[11]建立了车辆运动过程动力学模型，分析了车速、路面激励与车辆振动谱三者之间的关系。

以上研究中，研究人员建立了考虑履带影响的履带车辆振动模型，提高模型的计算精度，但并未对履带自身的振动特性、履带与车辆之间的相互作用关系以及履带如何影响履带车辆的振动进行深入的研究。

为了研究履带对车辆振动特性的影响，基于多体动力学原理建立了简化履带的柔性履带模型和复杂多刚体模型，采用特征值分析和功率谱分析等方法分析履带环的固有振动特性、履带与主动轮啮合过程中的多边形效应对车辆振动特性的影响。研究结果对定量分析履带车辆振动特性，进而改善履带车辆振动特性具有重要的意义。

1 履带车辆行驶系统动力学

为了开展履带对车辆振动响应特性的对比研究，分别建立了柔性履带简化模型和刚性履带约束模型，进而建立履带车辆行驶系统整车模型。

1.1 履带约束方程

为了简化履带柔性部分的建模，假设柔性履带是由不可伸长的带子环绕各轮而成，与各个车轮间为轴平行约束，与硬路面通过接触力约束。即柔性履带模型忽略履带板之间的相互作用，各车轮之间只有运动学约束关系，因而柔性履带模型无法反映履带的复杂振动特性。

根据履带板的几何尺寸构建单块履带板的几何实体模型，履带板间通过轴套约束，履带板与主动轮、负重轮、诱导轮及托带轮之间的相互作用按照接触力处理[12-13]。履带板由被橡胶轴套包裹的履带销依次连接。相邻履带板与连接销的作用力简化为履带销的轴套力和摩擦力矩，如图1所示。在忽略摩擦力矩的情况下，履带板间的接触力包括产生平动和转动效应的力和力矩，即

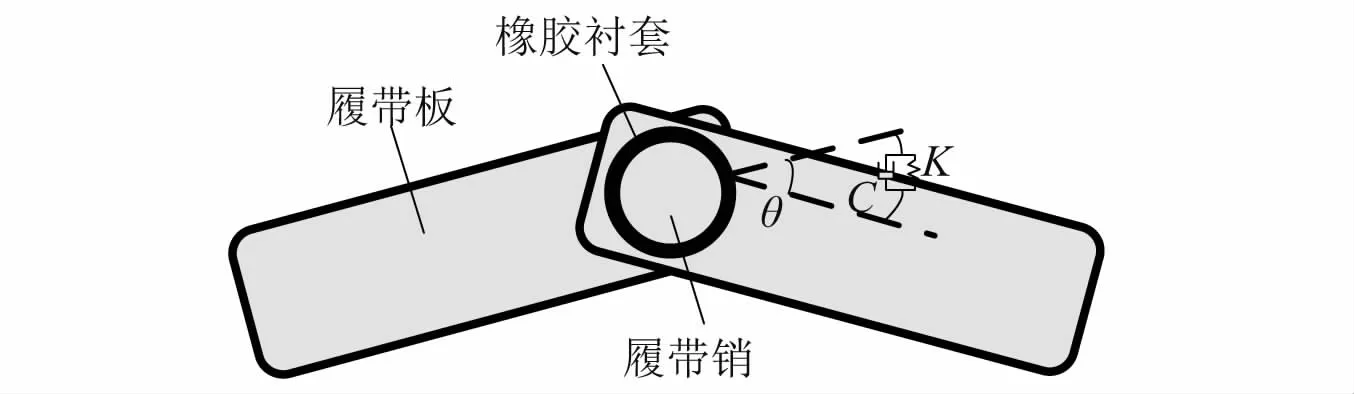
图1 履带板模型Fig.1 Track plate model

式中:KF和CF分别为履带连接销的平移刚度矩阵和阻尼矩阵；F0为预载荷；q和q·分别为作用点的位置和速度向量；KT和CT分别为履带销的扭转刚度矩阵和阻尼矩阵；θ和θ·分别为履带板间转动的角位移向量和角速度向量。

履带板与负重轮等各轮之间的相互作用力按接触力处理，各轮与履带板接触面的变形量为σi，接触力作用于接触面的法向，即

式中:k为刚度系数；c为阻尼系数。

履带板与地面之间的约束关系模型，当按硬路面处理时，假设履带板与路面接触点履带对地面的透穿深度为σz，则履带与地面间的接触力为

接触面上存在相对滑动的切向摩擦力。该摩擦力即为确保车辆能够提供可靠牵引力的地面附着力

式中:kr，cr为履带板与路面之间的刚度系数和阻尼系数；μ为摩擦因数。

各部件间的运动学约束以旋转副为主，对于刚体i和刚体j，旋转副约束方程为

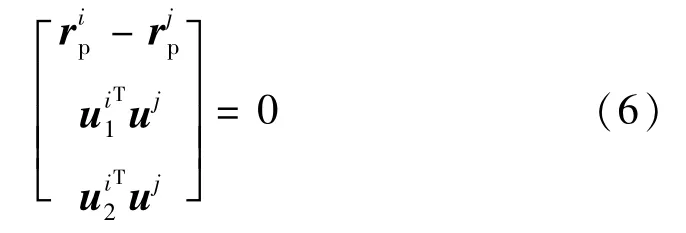
1.2 履带车辆模型拓扑结构

以某型号高速履带车辆为例，在建立车辆多体系统动力学模型时[14]，为了方便计算，作出如下简化:①所有部件均假设为刚体，其中，上装、动力传动系统与车身合并为单个质量块；②悬挂系统由平衡肘与车身间的弹簧阻尼力矩代替；③张紧机构中曲臂通过转动副连接诱导轮和车身，其传动装置简化为通过平动副和弹簧阻尼力约束的滑柱和套筒，二者通过转动副分别与车身、曲臂相约束。根据上述简化，结合履带车辆各部件间的连接关系，分别得到柔性履带和刚性履带车辆行驶系统拓扑结构图，如图2和图3所示。

图2 柔性履带行驶系统拓扑结构图Fig.2 Topological structure of drive system with flexible track

图3 刚性履带行驶系统拓扑结构图Fig.3 Topological structure of drive system with rigid track

系统拓扑结构图中的部件和约束详情见表1、表2。其中柔性履带车辆行驶系统模型由41个刚体和22个柔性履带组成，共有122个自由度。刚性履带车辆行驶系统模型由231个刚体组成，共有1 182个自由度。

表1 履带车辆行驶系统模型部件表Tab.1 Parts of drive system model

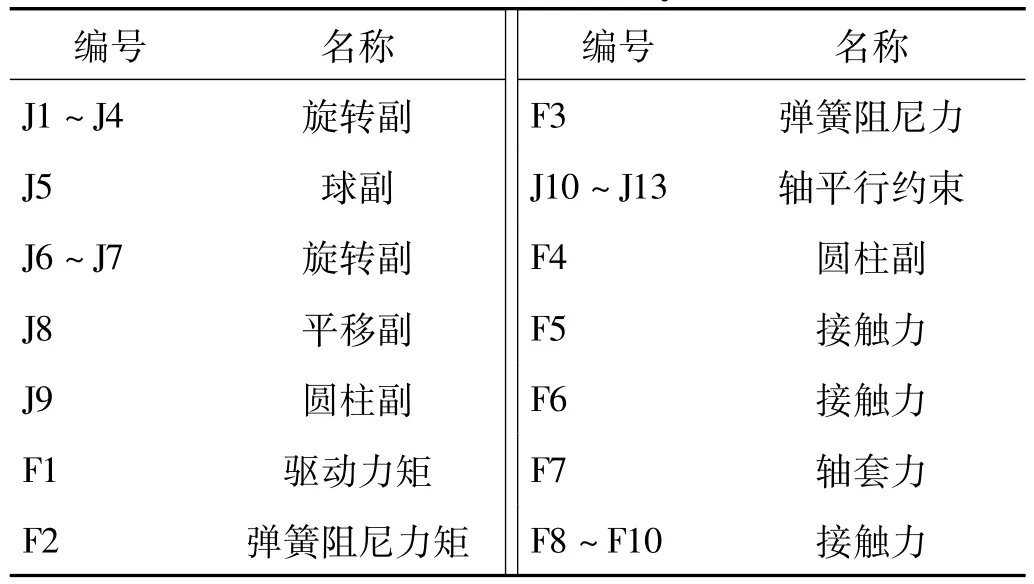
表2 履带车辆行驶系统模型约束表Tab.2 Constraints of drive system model

1.3 车辆行驶系统动力学方程

采用笛卡儿坐标系下的第一类拉格朗日方程建立高速履带车辆行驶系统动力学方程。刚体质心的笛卡尔坐标和反映刚体方位的欧拉角组成其广义坐标，即q=[x，y，z，ψ，θ，φ]T。 模型广义坐标矩阵为

履带车辆模型中刚体的约束方程为

式（8）对时间求导得到速度约束方程为

式中:Φq为约束方程的雅可比矩阵；q·为广义速度矩阵。

式（9）对时间求导得到加速度约束方程为

履带车辆模型中刚体的动力学方程为

式中:M为模型的广义质量矩阵；λ为拉格朗日乘子；Fe为广义外力矩阵；Fv为惯性力矩阵。

联立式（10）和式（11）得到的欧拉-拉格朗日方程组为

根据上述理论分析和车辆参数，构建履带车辆动力学模型并进行求解。

1.4 随机路面模型

车辆平顺性仿真需要构建多种路面。按照国际标准ISO2631，根据各种典型路面的实测功率谱密度，可将路面不平度等级分为A级～H级，路面行驶条件从A级～H级越来越恶劣，其中装甲车辆行驶路面一般为D级、E级和F级路面，例如搓板路、砂石路、起伏土路等。根据要生成的路面等级选取标准中相应的路面不平度系数Gq（n0），选用谐波叠加法计算得到路面不平度随机过程q（x）为

式中:x为路面纵向距离；φi为相角，为[0，2π]区间均匀分布的随机数；N为参考空间中心频率数；ni为在[nl，nu]区间内第i各参考空间的中心频率，每个区间长度为Δn；A为对应离散空间不平度幅值，即

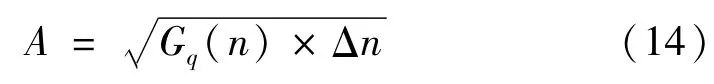
以E级路面为例，对各种典型随机路面环境进行模拟，E级路面和功率谱的仿真结果如图4和图5所示。

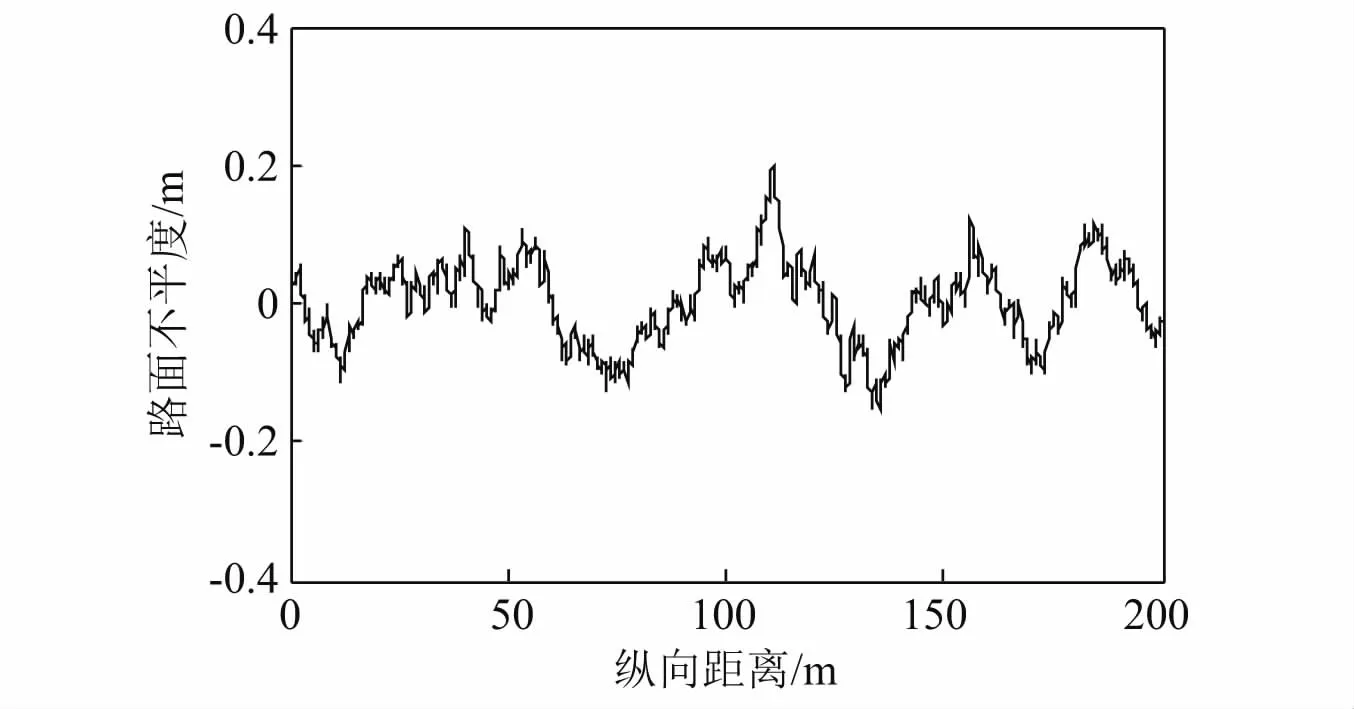
图4 E级路面模型Fig.4 Class E road model

2 履带振动特性分析

2.1 车辆振动响应

车辆行驶过程中，履带对车辆振动的影响主要体现在以下几个方面:

（1）路面激励通过履带传递时，由于履带板与地面近似为部分点接触，一方面相当于将路面离散成以履带板节距为间隔的路面，滤掉了路面激励中波长大于履带板节距的成分，使履带板的空间频率成为路面激励的空间频率上限；另一方面两块履带板间的连接处的振动又为路面不平度增添了周期性激励，其频率与履带板节距以及车速相关。

（2）履带与主动轮啮合过程中由于每块履带板有节距，造成了履带板与主动轮啮合形成的多边形效应。多边形效应的存在使啮合的履带板与主动轮之间产生较大的冲击振动，冲击振动的激振频率与履带板的节距以及车辆的行驶速度相关。

（3）一定数量的履带板环绕主动轮、负重轮、诱导轮、托带轮组成封闭链环。在车辆行驶过程中，履带环对行驶部分有几何约束和力学约束作用[15]。前者反映在履带环周长固定，后者体现为履带的张紧力。车辆通过不平路面时，车辆的俯仰角振动造成非驱动段履带长度和起履带牵引力的变化，迫使车辆产生“牵连”的纵向运动，有助于车身振动的减振。履带预张紧力会降低悬挂弹性元件对后续障碍物的缓冲作用，使车身的俯仰振动加剧。

由以上分析可知，履带板与地面之间的相互作用以及履带与主动轮啮合过程中产生的多边形效应主要影响车身高频部分的振动，而履带环的几何及力学约束主要影响车身低频部分的振动。

2.2 履带环振动固有特性分析

为了研究履带环的固有振动特性，将履带车辆多刚体模型中的履带环作为连续弹性体进行分析，非接地段履带环模型由第一负重轮、第六负重轮、诱导轮、主动轮和托带轮之间的六段履带组成，如图6所示。

图6 履带环模型Fig.6 Track circuit model

2.2.1 连续弹性体履带的振动分析

用连续弹性体模型来描述第段履带在平面内的运动，i=1，2，3，4，5，6。 图7表示第i段履带在自身重力作用下产生下垂，达到静平衡位置时近似为抛物线，其曲率为Ki，此时履带满足条件ki=KiLi＜1。令函数Vi（x，t），Ui（x，t）分别为履带纵向振动位移和横向振动位移。 其中:x为履带微元的位置坐标，x∈（0，Li）；t为时间变量。

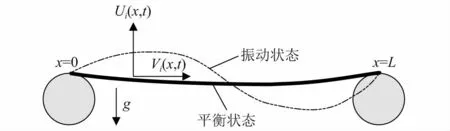
图7 第i段履带振动状态Fig.7 Vibration status of the i th track depart

由牛顿定律得到履带模型自由振动的运动微分方程为

其中，

式中:vl，vt分别为纵向波和横向波的传播速度；ρg为履带段的线密度；EA为履带段的轴向刚度；P0为履带段的预紧张力。

一般的履带模型中，通常将振动波传播的速度离散为横向和纵向速度，纵向传播速度远大于横向传播速度。基于这种情况，可认为履带的拉伸是准静态的，因此式（15）描述履带的纵向运动可近似为静态的，即

将式（18）进行两次积分，代入式（16）得

采用分离变量法，设各函数的解依次为

式中，ω为固有频率。将式（20）代入式（16）和式（19）得

其中，

将式（21）代入式（20）中得到第i段的纵向振动位移Vi（x，t）和横向振动位移Ui（x，t），通过履带自由振动振动的边界条件即可求解其各阶固有频率和模态振型。

2.2.2 履带环模型特征值计算

用于求解履带自由振动的边界条件如下。首先在主动轮、托带轮、诱导轮处，由履带位移的连续性可得前后两段履带的纵向位移相同，即

由力矩平衡方程得

其中，

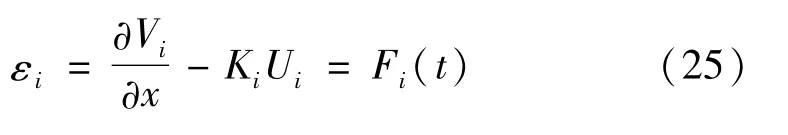
式中，εi为第i段履带环的动应变。按照之前所作的假设，各段履带环上发生的动应变完全一致，相邻履带环的动应变差值导致了其附着的各轮的转动。其转动角度与履带振动的纵向位移相关，即

不考虑负重轮的位移和主动轮与履带板啮合的多边形效应，则第一、第六负重轮处纵向位移和横向位移为0，主动轮、诱导轮、托带轮处横向位移为0，即

用已推导出的纵向振动位移和横向振动位移通解式（20）代入边界条件方程式（23）～式（28）中进行求解，得到的特征值方程为

式中:R（ω）为一个关于特征值的函数的矩阵；H为包含等常数项的特征矢量，即

采用特征值计算的方法求解履带环的振动固有频率，其中前5阶固有频率及其振型如图8所示。

图8 履带环前5阶模态振型Fig.8 The first 5 orders vibration model of rack circuit

由履带环固有特性的分析计算结果可以看出，履带环的振动固有频率主要在3～10 Hz的频带范围内，跟履带板与地面之间以及履带板与主动轮之间啮合产生的多边形效应的激振频率相比，属于低频振动。当车辆在典型起伏路面行驶时，地面的起伏波动很容易引起履带环的低频横向振动，造成上支履带环的上下波动，严重时上支履带板可能会撞击车身两侧的翼子板，对车辆造成一定的损伤。

3 履带车辆系统振动响应分析

为了研究履带对车辆整体振动响应的影响，分别对建立的柔性履带和刚性履带的车辆系统模型进行仿真分析，并对计算结果进行对比研究。

3.1 仿真工况

为研究履带对车辆振动的作用规律，进行上述两种模型在多种典型工况下的动力学仿真，输出给定激励下驾驶员座椅处的垂向振动响应信号。考虑不同路面等级和车速的影响，分别进行以20 km/h和30 km/h速度在D级、E级和F级随机路面下行驶工况的仿真计算。仿真过程的采样频率为200 Hz，采样时间为10 s（不包括落车以及车身恢复平稳时间）。

3.2 仿真结果分析

图9为仿真模型在F级路面30 km/h行驶工况下驾驶员座椅处的垂向加速度响应曲线的对比，从时域曲线可以看出，刚性履带模型中由于考虑了履带振动的影响，使时域曲线中刚性模型的峰值振动加速度要大于柔性履带模型。

图9 F级路面30 km/h垂向加速度曲线对比Fig.9 The vertical vibration acceleration signals at 30 km/h on class F road

采用Welch算法计算得到的各个工况下功率谱密度曲线对比，如图10所示。从中可以看出加速度信号的频率成分主要区分为低频段和高频段，其中低频成分的频率范围在15 Hz以内，高频成分的频率范围在30 Hz以上，只有刚性履带会激发高频成分。

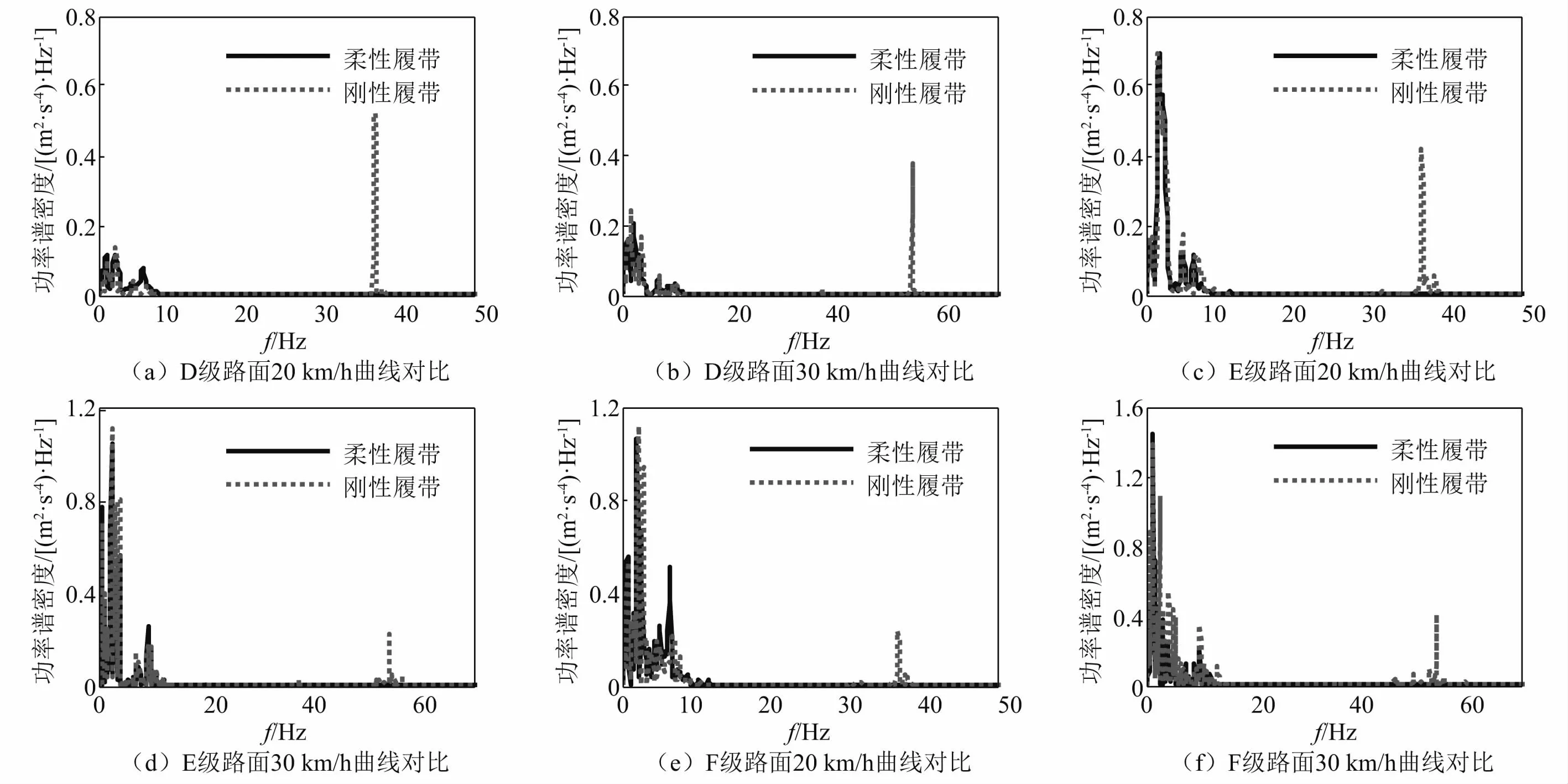
图10 各工况加速度功率谱密度曲线对比Fig.10 PSD of vibration acceleration signals in deferent conditions

功率谱密度曲线中，低频带1～2 Hz内主要反映的是车身的俯仰振动和垂直振动固有频率。在不同行驶工况下，俯仰振动的固有频率在0.8～1.0 Hz频率范围内变化，垂直振动的固有频率在1.3～2.0 Hz频率范围内变化。柔性履带模型和刚性履带模型计算得到的俯仰振动和垂直振动固有频率会有一定的差异，这主要是由于模型简化过程中，两种模型的整体质量、刚度等属性之间有一定差异造成的，同时刚性履带模型中，履带环的存在也会对车身俯仰和垂直振动产生一定影响。其中，图10（a）中由于车速较低、路面状况较好，俯仰振动频率不明显，柔性履带模型和刚性履带模型的垂直振动频率分别为1.36 Hz，1.37 Hz；图10（b）中两种模型的俯仰振动频率分别为0.78 Hz，0.97 Hz，垂直振动频率均为1.76 Hz；图10（c）、图10（d）、图10（e）中两种模型的俯仰振动频率均为0.97 Hz，前两者垂直振动频率分别为1.66 Hz，1.76 Hz，图10（e）中为2.05 Hz；图10（f）中两种模型的俯仰振动频率均为1.36 Hz，柔性履带整车模型的垂直振动频率为1.95 Hz，刚性履带模型中垂直振动不明显。

功率谱密度曲线中，4～10 Hz的较低频带范围内主要包含负重轮轴距引起的轴距效应以及履带环的整体振动效应，柔性履带模型中，由于不考虑履带环的几何约束作用，轴距效应相对更加显著，而履带环的几何效应会对刚性履带模型中的轴距效应起一定的抑止作用，但是刚性履带环固有振动效应会比较显著。

功率谱密度曲线中，30～60 Hz的高频成分主要为刚性履带板节距引起的周期性激励以及履带与主动轮啮合产生的多边形效应引起的激振频率，其频率大小与节距l、车速u相关，即

选定车型的履带板节距为0.153 m，当车辆分别以20 km/h和30 km/h车速行驶时，对应的履带板激振频率分别为36.33 Hz和54.64 Hz。 图10（a）、图10（c）、图10（e）中，由刚性履带模型计算得到的相应峰值频率分别为35.16 Hz，36.91 Hz和35.55 Hz；图10（b）、图10（d）、图10（f）中计算得到的峰值频率分别为54.32 Hz，54.35 Hz，54.14 Hz。 从中可以看出，仿真计算与理论推算结果具有很好的一致性。而柔性履带模型中，由于不考虑履带的多边形效应，因而无法反映履带的高频振动的影响。

通过计算功率谱密度的均方根值来定量分析履带对车身振动的影响，按式（32）计算

式中:Ga（f）为功率谱密度函数；fu为计算频率上限。表3给出了两种模型驾驶员座椅处垂向振动加速度功率谱密度均方根值的对比结果。

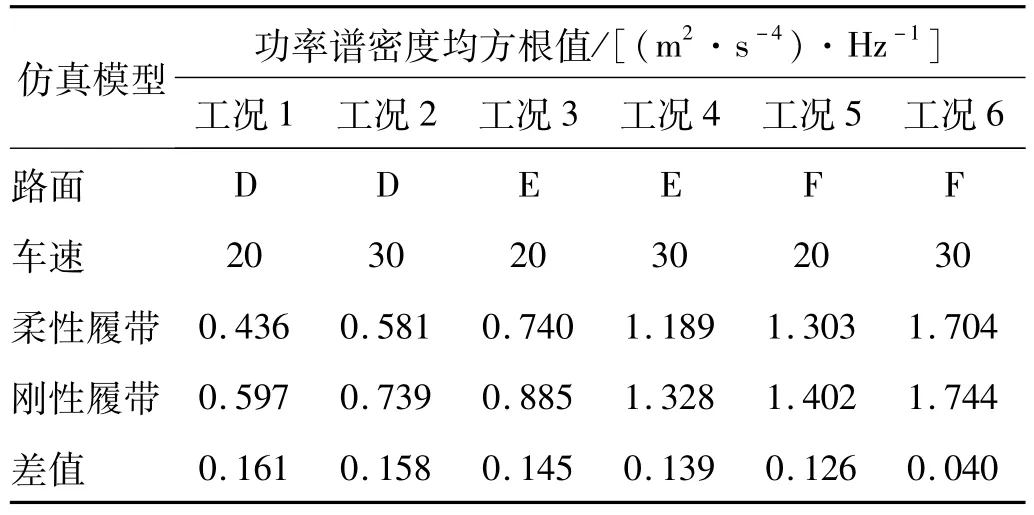
表3 振动功率谱密度均方根值对比Tab.3 RMScomparison of vibration PSD

对柔性履带和刚性履带车辆模型的功率谱计算得到，履带部分的振动能量占车辆系统整体振动能量的10%～25%左右。工况6由于路面条件恶劣，履带车辆的低频振动加剧，履带对车辆振动的影响极小。从表3中柔性履带和刚性履带均方根值的差值来看，从D～F，其差值越来越小，也就是说二者差别减小，因此随着路面不平度等级的降低，履带环因素对车辆振动的影响越来越小；随着车速的升高，履带部分的振动影响同样有所下降。

4 实车试验验证

在某试验场进行高速履带车辆振动试验，测试装置及试验道路如图11所示，通过数据采集系统采集车辆行驶过程中炮长座椅处垂向加速度信号。

图11 实车试验装置及道路Fig.11 Test system and road for vehicle test

图12为某试验场进行的高速履带车辆振动试验中，保持车辆在30 km/h左右的时间段，车辆行驶速度随时间的变化曲线。试验道路为实测路面不平度等级为E级的典型越野路面，以1 kHz的采样频率分别采集车辆平均速度为20 km/h和30 km/h时的测试信号。试验过程中测得主动轮转速，将其加载到仿真模型的主动轮上以驱动车辆仿真。

图12 试验车速-时间变化曲线Fig.12 The speed signal of vehicle

选取车速为20 km/h和30 km/h时炮长座椅处的垂向加速度测试信号进行频谱分析，得到的功率谱密度曲线与相同工况下的柔性履带模型和刚性履带模型得仿真结果对比，如图13、图14所示。

图13 20 km/h时功率谱密度曲线对比Fig.13 Comparison of PSD at 20 km/h

图14 30 km/h时功率谱密度曲线对比Fig.14 Comparison of PSD at 30 km/h

综合图13、图14可以看到，实车振动的高频成分频带范围较宽，这是由于实车试验中速度呈现较大的扰动性，使与履带板节距相关的激振频率不断变化导致的。例如图12中车速在24.2～34.5 km/h内变化，相应的高频振动频率在53～62 Hz。图13、图14中，仿真结果与试验结果的低频振动响应一致，刚性履带模型的高频振动峰值频率与试验结果相近，而柔性履带模型没有高频振动响应。因此，可认为所建立的刚性履带车辆动力学模型较为合理，其仿真结果具有一定的参考价值，能较为真实地反映实车振动响应特性。其中，刚性履带模型要比柔性履带模型与试验结果更接近，而柔性履带模型计算效率相对较高，在实际中可以根据精度要求来选择刚性履带模型或柔性履带模型进行仿真计算。

5 结 论

对履带振动特性的研究结果对于定量描述履带对车辆振动特性的影响，并进而改善履带车辆的振动特性具有重要的意义。

（1）采用多体动力学方法建立了包含柔性履带和刚性履带的履带车辆行驶系统模型。采用特征值分析的方法计算了履带环的固有振动特性。采用功率谱分析的方法研究了履带与地面激振频率、履带与主动轮啮合过程中的多边形效应等对车辆振动特性的影响。

（2）计算结果表明，履带环的固有振动频率在3～10 Hz的较低频带范围。当车辆在典型起伏路面行驶时，地面低频激励容易引起履带环的振动。而履带板与地面之间的相互作用以及履带板与主动轮啮合时引起的多边形效应会引起车辆的高频振动，振动频率与履带板节距以及车速相关。

（3）从柔性履带和刚性履带车辆模型的功率谱计算来看，一般工况下履带部分的振动能量占车辆系统整体振动能量的10%～25%；随着路面状况的恶劣或者车速的提升，履带对车辆振动的影响逐渐变小。通过试验数据的对比表明，刚性履带模型的计算结果与试验结果更加接近。