基于蚁群优化支持向量机的室内定位算法

张龙飞，金仁成，姚永伦

(大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024)

0 引言

随着网络技术的快速发展，人们对室内定位技术的需求也越来越高，基于信道状态信息(Channel State Information，CSI)的室内定位技术成为研究热点，尤其是基于位置指纹的定位方法，该方法因其成本低廉、方法简易的优势逐渐成为室内定位的主流，它的定位过程包括两个部分：离线训练阶段和在线定位阶段。离线阶段在室内预先选好的参考点接收CSI数据包，提取出指纹信息，并建立指纹数据库；在线阶段将测试点的指纹信息与数据库中的指纹信息进行匹配。常用的匹配算法有支持向量机(Support Vector Machine，SVM)[1]和神经网络[2]等方法，使用主成分分析(Principal Component Analysis，PCA)可以降低数据维度和去除高频噪声[3]，减小定位计算复杂度。

党小超等[4]首先使用粒子群优化支持向量机(PSO_SVM)的算法提高室内定位精度；刘旭明等[5]提出了遗传算法优化的支持向量机(GA_SVM)以提高室内定位精度；秦军利等[6]说明了蚁群优化支持向量机(ACO_SVM)的应用场景，但未运用到室内定位中。本文提出了一种基于蚁群优化支持向量机的室内定位算法。

1 蚁群优化支持向量机算法

1.1 信道状态信息

CSI是基于正交频分复用调制技术的无线信号在移动终端的信道响应表现形式。因为接收端有3根天线，并且每根天线有30个信道，所以每个CSI数据包是3×30的矩阵，如式(1)所示：

(1)

其中：Hxy为CSI的第x根天线的第y个子载波，包含着幅值和相位信息，如式(2)所示：

Hxy=‖Hxy‖ej∠Hxy.

(2)

其中：‖Hxy‖为Hxy的幅值；∠Hxy为Hxy的相位角。

由于硬件条件等影响，CSI的相位角会偏移，没有矫正的相位信息是无法作为指纹的。YANG I 等[7]提出了线性变化的方法对杂乱的相位信息进行矫正，得到了真实相位，线性变换处理前、后的相位信息如图1和图2所示。

图1 线性变换前CSI相位角

图2 线性变换后CSI相位角

由此，可以得到数据包的幅值矩阵Hamp和相位角矩阵Hangle：

(3)

(4)

1.2 改进的蚁群算法支持向量机

1.2.1 数据的预处理

实验表明，CSI的数据特征越多，定位精度越高，为此，本文融合了Hamp和Hangle，先将它们由3×30的矩阵展开成1×90的矩阵，然后把两个矩阵结合成一个1×180的矩阵Hs，如公式(5)所示:

Hs=[‖H11‖,…,‖H1N‖,‖H21‖,…,‖H2N‖,

‖H31‖,…,‖H3N‖,∠H11,…,∠H1N,

∠H21,…,∠H2N,∠H31,…,∠H3N].

(5)

按照这种方式，把所有的数据包都转成式(5)格式，并把每10个数据包分成一组，求出对应子载波的幅值和相位的方差，结果如式(6)所示：

Hδ=[δ‖H11‖,…,δ‖H1N‖,δ‖H21‖,…δ‖H2N‖,

δ‖H31‖,…,δ‖H3N‖,δ∠H11,…,δ∠H1N,

δ∠H21,…,δ∠H2N,δ∠H31,…,δ∠H3N].

(6)

对应子载波方差的大小更能反映出受环境等因素影响而产生的波动性，其特征更具有分辨性，定位精度会更高。

1.2.2 改进的算法流程

根据SVM参数优化[8]思想，我们把提出的改进算法命名为ACO_SVM_VAR，其目的是找出SVM中最优的惩罚系数c和核函数参数g，使得定位误差最小，算法流程如图3所示。

图3 ACO_SVM_VAR算法流程

2 实验环境

我们在大连理工大学机械学院9楼的室内进行实验，实验环境如图4所示，该区域面积为70 m2，在定位区域中选取80个参考点，并选取10个测试点。接收端为联想笔记本电脑，发送端为路由器。每个点处接收1 000个数据包进行分析。

图4 实验场景

3 实验分析

为了直观地对比出改进算法ACO_SVM_VAR的定位效果，将它的定位效果与ACO_SVM、GA_SVM和PSO_SVM算法进行了对比，10个测试点的定位如图5所示。其中，实心圆点为测试点的真实坐标，叉形点、空心圆点、菱形点、方形点分别为ACO_SVM_VAR、ACO_SVM、PSO_SVM、GA_SVM算法计算出的测试点坐标。

图5 各算法定位误差对比

4种算法求得的c和g参数值如表1所示，并求出了它们的平均定位误差。

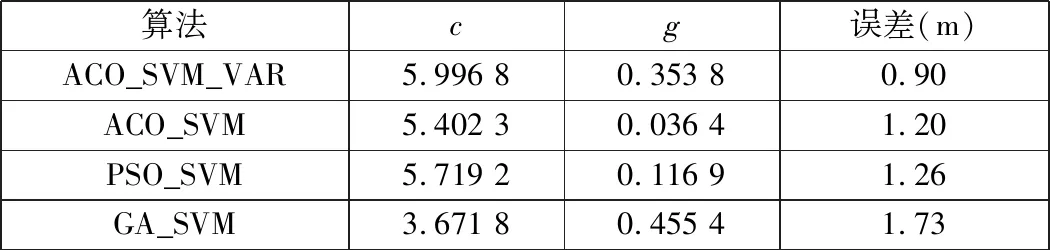
表1 不同算法的定位误差

由图5可以看出：多数点的定位效果ACO_SVM_VAR优于ACO_SVM、PSO_SVM和GA_SVM算法。由表1可知，ACO_SVM_VAR、ACO_SVM、PSO_SVM、GA_SVM算法的平均定位误差分别为0.90 m、1.20 m、1.26 m、1.73 m，本文提出的算法定位精度分别比ACO_SVM、PSO_SVM和GA_SVM算法提升了25%、29%和48%。

对于所有实数x，累积分布函数定义如下：

F(x)=P(X≤x).

(7)

对离散变量，累积分布函数表示所有小于等于x的值出现的概率和。

定位误差累积分布中的每个点代表定位误差距离在x(m)内其分布概率的大小，相同误差距离时，分布概率越大，定位效果越好。对ACO_SVM_VAR、ACO_SVM、PSO_SVM和GA_SVM算法的定位误差累积分布概率如图6所示。从图6中可以看出：ACO_SVM_VAR算法的定位误差概率最快达到1，定位效果最好；ACO_SVM和PSO_SVM算法定位误差概率交叉分布，效果十分接近，而GA_SVM算法定位误差概率最慢达到1，定位效果最差。

图6 不同算法的定位误差累积分布概率对比

当定位误差小于1 m时，ACO_SVM_VAR、ACO_SVM、PSO_SVM和GA_SVM算法的1 m内误差点数占总点数的比例分别为50%、50%、40%和40%。当定位误差大于1 m时，ACO_SVM_VAR算法的定位误差概率很快升到1，明显好于其他算法。

4 结束语

本文创新地将ACO_SVM运用到室内定位，并提出了改进的蚁群优化的SVM室内定位算法(ACO_SVM_VAR)，结合了CSI的幅值和相位信息，该算法与ACO_SVM、PSO_SVM和GA_SVM算法相比，平均定位精度分别提升了25%、29%和48%，有效提升了室内定位精度。