研磨子磨耗增粘过程的仿真分析*

张正桥，曾 京

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

伴随着1964年世界上第一条高速铁路的通车运营，研磨子应运而生，并在随后的半个多世纪内广泛应用于高速列车和城轨车辆的制动系统中，起到了良好的轮轨增粘和踏面修型效果[1]。我国也在动车组和城轨列车中大量应用研磨子，通过大量现场及跟踪试验数据发现：研磨子可以清除幅值较小的车轮多边形并持续抑制其发展[2]；另外，研磨子可以减缓踏面等效锥度的增长并起到一定的修型作用，维持较好的车辆横向稳定性。

鉴于研磨子的材料和作用过程较为复杂，国内的相关研究还停留在表面的试验现象分析阶段。本文以高速列车上配备的研磨子为对象，从基本磨耗机理出发，通过试验分析和有限元仿真，探讨研磨子磨耗增粘过程的变化和性质，明确关键工作参数对磨耗过程的影响，以期为研磨子的作用机理研究和作用策略优化提供参考。

1 磨耗原理及过程分析

1.1 粘着磨耗

两个金属摩擦副在一定载荷下接触时表面微凸体相互碰撞并发生塑性变形，接触面形成粘着结点，当两固体受力产生相对滑动时微凸体发生剪切断裂，材料可能脱落成磨屑或迁移到另一方材料表面，这类磨耗叫做粘着磨耗[3]。粘着磨耗初期两方材料摩擦剧烈，随着磨耗的进行，材料相互磨合，微粒接触逐渐紧密，接触应力减小，磨耗量和磨耗速率逐渐降低[4]。

1.2 磨粒磨耗

硬质磨粒在外加载荷的作用下压入软质材料并进行刮擦和切削，从而引发较软材料机械损耗的过程称为磨粒磨耗，当比磨耗量(磨耗率与载荷之比)小于10-9mm2/N时发生定常磨耗，即磨耗率随时间变化基本稳定不变，否则发生严重磨耗[5]。磨粒磨耗按照磨粒形状又分为圆锥磨耗、球形磨耗等，Rabinowicz等[6]首先以圆锥磨粒建立了经典的磨粒磨耗理论模型，如图1所示，假定单颗圆锥体磨粒半顶角为θ，在载荷P的作用下压入较软材料中，压入深度为h，压入部分的半径为r，压入圆截面面积为A=πr2。

图1 圆锥磨粒磨耗模型

由布氏硬度的定义可知，被磨金属材料的硬度H等于载荷P与压入面积A之比。圆锥形磨粒沿材料表面滑移l形成的沟槽体积即为该单磨粒造成的磨耗体积，通过补形得到该磨耗体为一个三棱柱，体积为：

(1)

整理可得圆锥磨粒磨耗模型磨耗率为：

(2)

同理，建立如图2所示的球形磨粒磨耗模型。假设球形磨粒压入深度为h，球体的半径为R，球体压入截面半径为r，总磨耗率可以表示为：

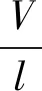
(3)

图2中灰色直角三角形区域满足几何关系：

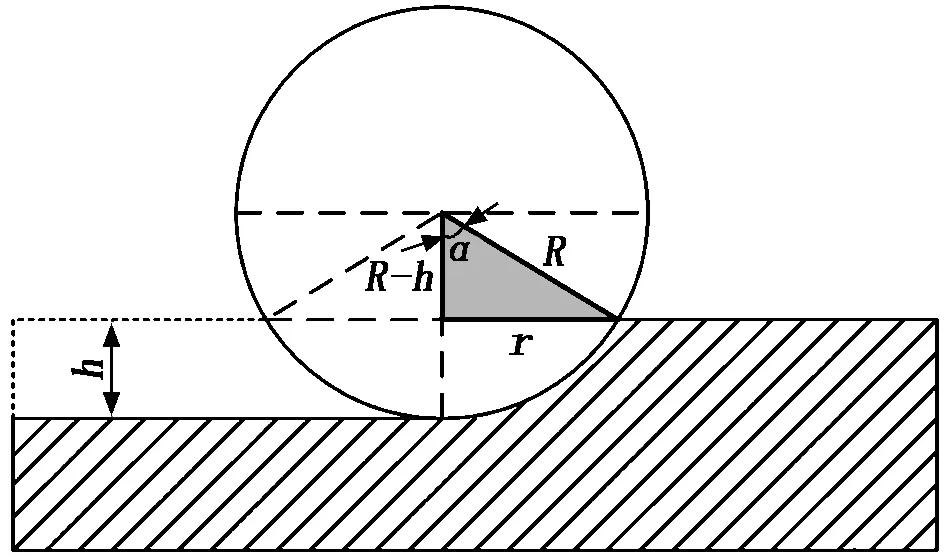
图2 球形磨粒磨耗模型

(4)

将式(3)和式(4)整理后可得磨耗率为：

(5)

1.3 研磨子与车轮的磨耗试验

日本铁道综合技术研究所[7]利用轮轨高速接触疲劳试验台进行了4组磨耗试验，试验工况及目的见表1。试验③、试验④中磨耗体积分为研磨子分和除去分，分别代表研磨子造成的踏面磨耗和纯轮轨接触磨耗。

表1 磨耗试验工况及目的

踏面磨耗速率随走行距离的变化关系如图3所示。图3中：A区域对比了无加振条件下有、无研磨子对踏面磨耗率的影响；B区域显示研磨子造成的踏面磨耗率；C区域对比了加振条件下有、无研磨子对踏面磨耗速率的影响。

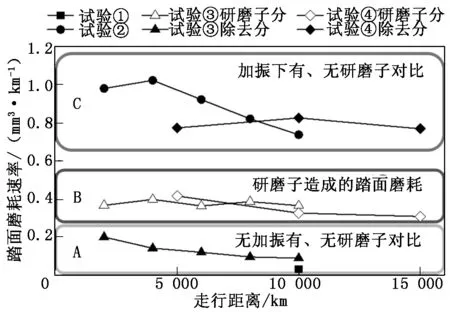
图3 4组试验的踏面磨耗速率曲线

A、C两区域磨耗率差距明显，可得出左、右激振是影响踏面凹坑磨耗的主要因素。

B区域中研磨子造成的踏面磨耗速率始终保持在0.4 mm3/km左右，没有出现较大波动。该试验中车轮载荷约为4 kN，按式(6)计算研磨子与车轮的比磨耗量为10-10mm2/N，故判断出该试验中研磨子与踏面的磨耗过程属于定常磨粒磨耗，研磨子造成的磨耗体积与走行距离成正比关系。

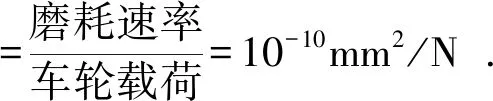
(6)

C区域中试验②走行中后期磨耗速率发生大幅度降低，符合粘着磨耗率的变化特征；试验④的磨耗曲线显示踏面磨耗率始终在0.8 mm3/km附近小幅波动，未出现明显降低趋势，可以证明研磨子的加入影响了轮轨接触向稳定磨耗阶段的转换，改变了轮轨磨耗的性质。

C区域中轮轨磨耗初期试验④的磨耗速率比试验②小得多，这是由于相比于轮轨前期磨耗率较大的磨合阶段，研磨子在初期通过与车轮踏面的磨粒磨耗使得踏面上附着了大量研磨颗粒，阻止了踏面金属材料与钢轨之间的一部分粘着磨耗作用；随着磨耗持续进行，踏面表面粗糙度不断增加，轮轨粘着系数变大，磨耗速率相应缓慢增加，但随着走行距离增加，踏面凹坑深度增加，研磨子表面和车轮凹坑内部材料接触减少，故磨耗速率缓慢减小。

2 磨粒磨耗模型建立

轮轨潮湿时，研磨子在一定压力作用下压在车轮踏面上，可以在磨粒磨耗的作用下增加踏面表面微凸体的数量，提升踏面粗糙度；另外，研磨子摩擦过程中不断脱落硬质颗粒并附着在轮轨接触表面上，随着车轮的转动嵌入车轮和钢轨之间，这些固体颗粒可以突破介于轮轨间的水膜，分担一部分垂向载荷并提供纵向粘着力，提高粘着性能，研磨子的增粘功能通过与车轮的磨耗作用得以实现。基于上文对两者磨耗类型的确定，在ABAQUS软件中建立球形和圆锥形二维单磨粒磨耗有限元模型。

在研磨子的磨耗过程中车轮在强载荷下处于高压和高应变率的状态，故应用Johnson-Cook本构模型来近似模拟车轮材料的塑性变形行为，其表达式如下：

(7)

其中：σy为流动应力；εp为等效塑性应变；εr为应变率；εr0为准静态应变率；T为当前温度；Tr为室温；Tm为熔点；A、B、C、m、n为应力应变参数，具体数值由实验确定。表2为车轮钢的力学性能和Johnson-Cook磨耗模型参数[8]。

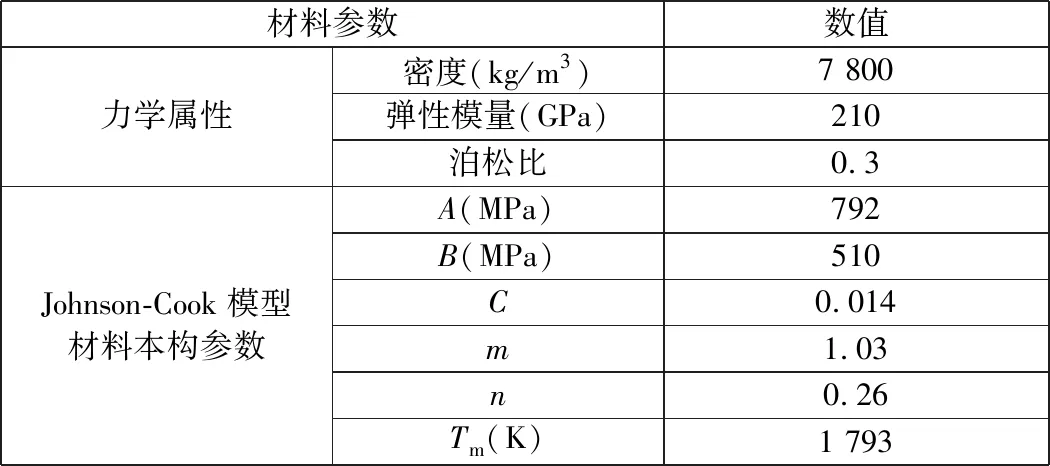
表2 车轮钢的力学性能和Johnson-Cook磨耗模型参数

设置被磨材料长20 μm、高10 μm，刚性硬质磨粒的最大滑动距离为10 μm；相互作用选择通用接触，切向行为选取罚函数形式，法向行为选取硬接触形式；除初始分析步外添加三个分析步，分别代表磨粒压入材料、横移划擦和卸载过程。

对模型进行仿真后得到磨耗过程的应力应变云图，如图4～图6所示。由图4和图5可以观察到：球形磨粒在划擦阶段前方及下方材料的塑性应变应力相比于压入阶段较为严重，表面材料受到接触应力的挤压作用后沿横向划擦方向发生了明显的塑性流动，这部分材料已发生严重的塑性变形，很容易在下次划擦作用中被磨去；磨粒卸载后材料表面可以发现存在残余应力以及显著的塑性变形。

图4 球形磨粒磨耗过程材料等效塑性应变云图

图5 球形磨粒磨耗过程材料等效应力云图

由图6可观察到：圆锥形磨粒使材料表面形成隆起，前期并未出现材料流失现象，即处于犁耕阶段；中后期磨粒继续推动前方材料产生堆积现象，部分材料受到的应力超过其屈服极限后发生严重塑性变形，在明显的显微切削作用下产生切屑。

图6 圆锥磨粒磨耗过程材料等效应力云图

3 研磨子磨耗增粘过程的关键参数

磨粒磨耗过程中划擦法向力和切向力决定了研磨子的磨耗增粘效果，依次改变模型参数观察划擦切向力的变化。

3.1 研磨速度

设置磨粒压入深度为1 μm，摩擦因数为0.4，磨粒研磨速度分别为50 m/s、100 m/s、150 m/s、200 m/s，得到的研磨速度对磨粒磨耗的影响如图7所示。由图7可知：不同速度下划擦法向力及切向力的最值和变化规律基本一致，但研磨速度较低时可以在较长时间内维持稳定的磨耗效果，而研磨速度较高时划擦力变化幅度较大，更容易产生非均匀磨耗。研磨子更适合在盘式制动过程中同步作用于车轮踏面以降低磨耗量并起到协同制动的作用。

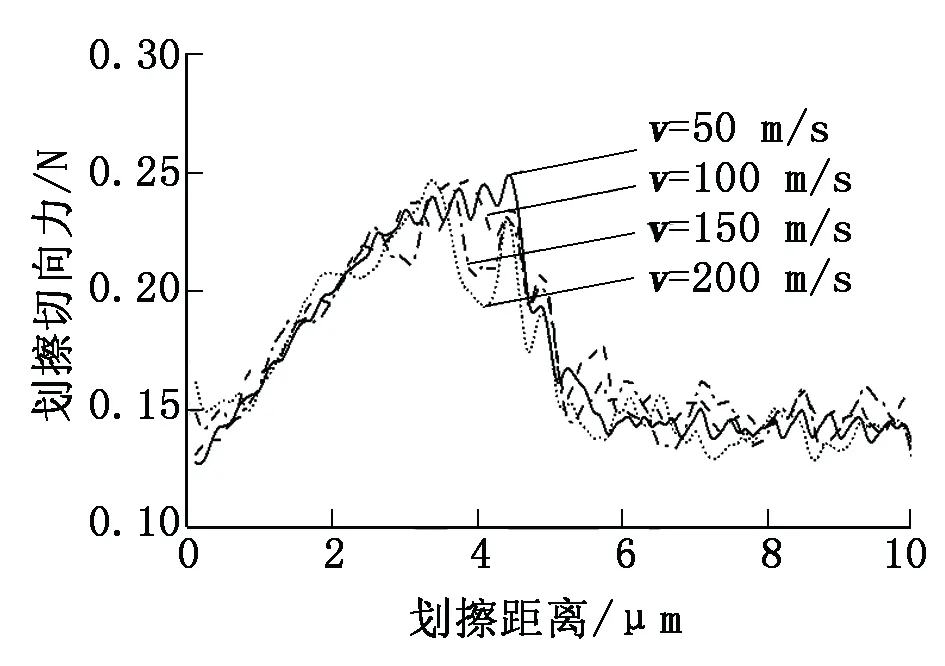
图7 研磨速度v对磨粒磨耗的影响

3.2 压入深度

设置磨粒研磨速度为50 m/s，摩擦因数为0.4，磨粒压入深度分别为0.5 μm、1 μm、2 μm、3 μm、4 μm，得到的压入深度对磨粒磨耗的影响如图8所示。由图8可知:随着压入深度的增加，磨粒与被磨材料的接触面积增大，两者之间的摩擦挤压作用力也相应增大;压入深度越小，磨耗就越先进入到稳定阶段，即划擦力与材料内部应力相互平衡的阶段;此外，h=3μm和h=4 μm两种工况的划擦力的变化趋势基本相同，此时对于半径为5 μm的磨粒来说压入载荷及深度过大，材料堆积和应力集中现象严重，划擦力呈异常上升趋势，车轮表面会形成明显的塑性流变层从而加重塑性变形，出现异常磨耗。实际应用中应注意在研磨子可以实现功能的前提下施加适当的作用压力。

图8 压入深度h对磨粒磨耗的影响

3.3 摩擦因数

设置磨粒研磨速度为50 m/s，压入深度为1 μm，磨粒与被磨材料间的摩擦因数分别为0.3、0.4、0.5,得到的摩擦因素对磨粒磨耗的影响如图9所示。由图9可以看出：随着摩擦因数增大，被磨材料表面微凸体增多，作用于材料的划擦力按一定比例增大，更容易产生残余应力进而产生磨屑。

图9 摩擦因数μ对磨粒磨耗的影响 图10 磨粒半径对磨粒磨耗的影响 图11 磨粒数量对磨粒磨耗的影响

3.4 磨粒半径及数量

Roylance等[9]通过试验得到了磨粒数量N和磨粒半径R的关系式N=555e-0.36R。根据前述磨耗率公式(5)画出球形磨耗过程中磨粒半径和磨粒数量对磨耗率的影响曲线，如图10和图11所示。从图10和图11可以看出：磨粒磨耗率随着磨粒半径的增大而增大，增速逐渐减缓；而随着磨粒数量的增加而减小。这是因为在磨粒总体积不变的情况下磨粒数量增多后磨粒尺寸减小，单个磨粒的作用力减小；同时磨粒与被磨材料接触不充分，起到了固体润滑剂的作用。可以推测：在保证磨粒尺寸不变的情况下，初始阶段磨耗率随着磨粒数量的增多而增大，但后期磨耗率基本维持定值。

4 结论

(1)基于对研磨子与车轮踏面磨粒磨耗过程的判定，利用ABAQUS软件分别建立了球形及圆锥磨粒磨耗模型，对比分析了研磨子磨耗增粘过程中车轮材料的应力应变的变化过程。

(2)分析了研磨过程中关键参数研磨速度、压入深度、摩擦因数、磨粒半径及数量对磨耗过程的影响规律，为研磨子作用参数的优化和控制策略的制定提供了依据。