基于剩余强度退化的FPSO系泊系统疲劳时变可靠性评估
赵 岩,余建星,2,余 杨,王华昆,王福程
(1.天津大学a.水利工程仿真与安全国家重点实验室;b.天津市港口与海洋工程重点实验室,天津 300072;2.北部湾大学机械与船舶海洋工程学院,广西 钦州 535011)
0 引 言
浮式生产储油卸油装置(FPSO)通过系泊系统定位于某一特定海域,服役时间往往长达几十年,属于永久系泊范畴,对于永久系泊的海上结构物,因系泊链长期受到外部环境条件变化引起的循环载荷作用,将引起疲劳损伤,因此有必要对其进行疲劳寿命分析。
可靠性是评价构件的重要设计指标,尤其适合不确定性较强的海洋工程结构设计。Wirsching等[1]综述了一些疲劳可靠性研究成果,研究了海洋结构物设计中疲劳可靠性方法的应用,该类基于SN曲线与线性疲劳累积准则的传统方法被广泛应用于海洋工程结构疲劳可靠性研究[2],但此类方法尚未考虑可靠性的时变性。而在实际中,由于强度和载荷的不确定性、强度的退化等,强度和载荷的相对关系在不断地发生变化,零部件和系统的可靠度和失效率显然应随载荷的作用次数或使用时间而变化,时变性是构件强度的典型特征。
在海洋工程领域,时变可靠性指标为构件的设计提供可靠依据,且有助于制定针对性的检修方案,具有良好的工程实用价值[3]。当前时变可靠性模型的建立大多考虑了腐蚀的影响[4-6]。而在疲劳时变可靠性方面,余建星等[7]基于设计寿命可靠性理论对张力腿平台建立了时变可靠性评估模型;刘勇等[8]基于首次超越失效准则计算了老龄导管架平台,建立了时变可靠性模型,两者均基于Miner线性累积损伤理论的破坏准则。目前对基于剩余强度退化机理的疲劳时变可靠性研究较少,且集中于机械构件的结构可靠性[9]。如王正等[10]基于一种构件抗力衰减模型、载荷强度干涉理论,考虑载荷与初始构件抗力不确定性,建立了机械构件疲劳时变可靠性模型;方永锋等[11]在该模型基础上建立了多次随机载荷作用下的结构时变可靠性预测的概率密度演化方法。
本文在以上研究的基础上,首次将剩余强度退化的时变可靠性模型与海洋工程疲劳计算结合,以内转塔式FPSO系泊系统为例,给出一种多工况、风浪流联合作用下的FPSO系泊系统时变可靠性评估方法。
1 疲劳时变可靠性分析方法
1.1 剩余强度退化理论
在循环疲劳载荷作用下,构件材料内部的损伤不断累积,疲劳损伤的发展必然会引起材料内部微观结构的变化,使材料的静态力学性能退化。迄今不少学者已基于试验研究提出了多种剩余强度退化理论[12],本文选用文献[13]提出的对数退化模型:
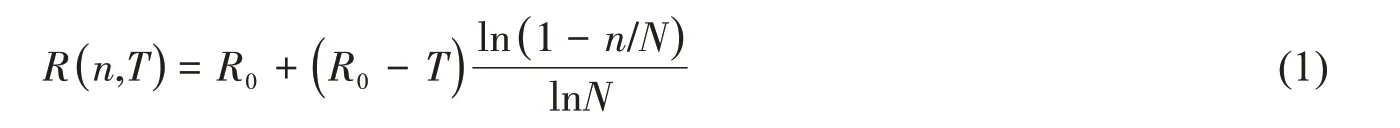
式中,R()n,T为拉力变程T的循环载荷下加载n次后的剩余强度;R0为初始强度;N为在拉力变程T的常幅循环载荷作用下的疲劳寿命,对于系泊链,该值可以在T-N曲线上获取:

式中,K、M为T-N曲线参数。
对于变幅载荷,文献[14]建立了多级载荷作用下剩余强度的等损伤比估计方法模型,将变幅载荷作用等效为恒幅载荷,本文参考其方法,获得了任意两级载荷等效公式:
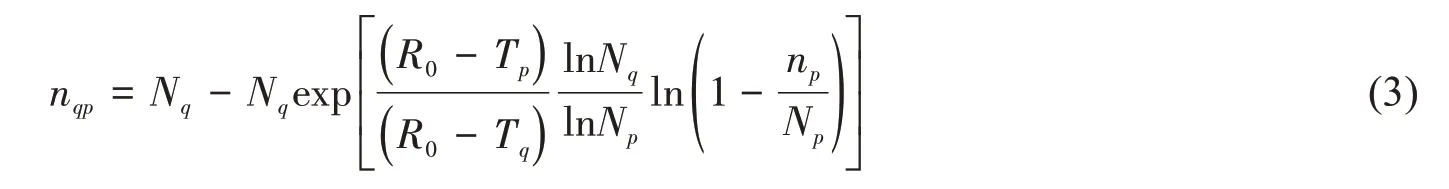
式中,p和q为任意载荷级数,即在载荷Tp作用下经历了np次循环,其造成的损伤若换算成载荷Tq作用时,载荷Tq需经历nqp次循环才能达到同样的损伤。
考虑海洋工程载荷的强随机性,通过雨流计数法进行计数的海洋工程载荷,各级载荷变程范围较大。本文引入基准载荷以简化计算,可得到多级循环载荷作用后的剩余强度为
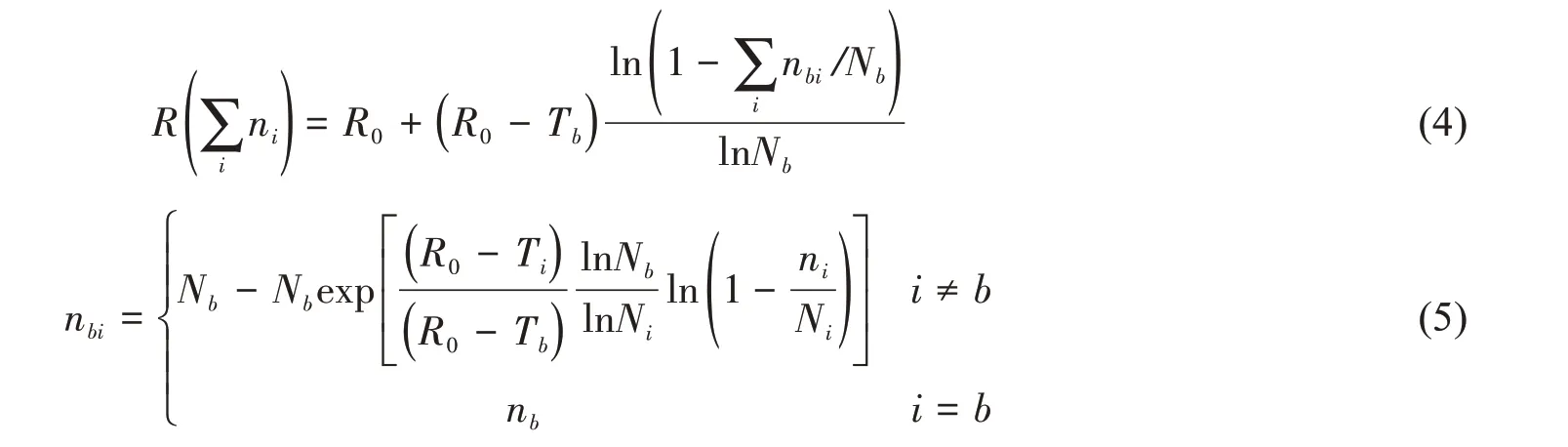
式中,ni为第i级载荷的循环数,b为基准载荷级数。

海洋结构物工况的长期状态通常看成是由许多短期工况的序列所组成,则在多种工况下的单位时长的疲劳等效循环数为

式中,nequk为k工况下单位时长疲劳等效循环数,pk为短期海况出现频率。
不考虑海洋环境的变化与每一单位时长内的构件抗力衰减,可以得到第ω单位时长内的构件强度为
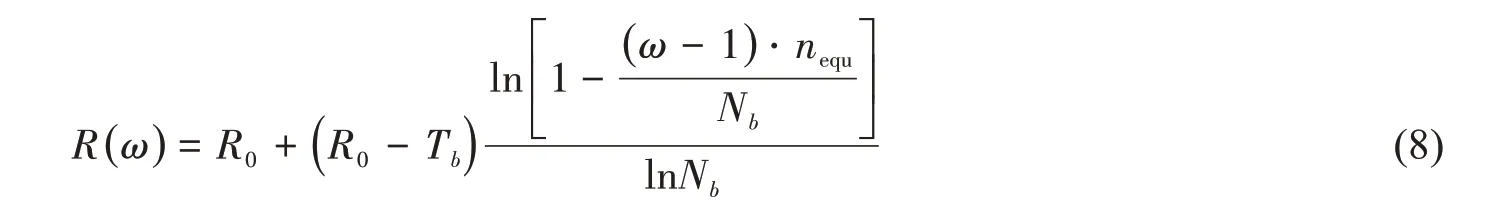
1.2 载荷分布估计模型
在单位时间内,载荷的最大值超过构件剩余强度即认为构件失效。为确定载荷最大值的概率分布,提取每种工况研究时段的所有极大值点并统计各级载荷出现频率,多工况加权后可得到长期载荷极大值的频率分布,可认为其近似符合正态分布,获取其分布参数。
而单一研究时段的最大值即为所有极大值中的最大值,文献[15]认为多个相同正态分布变量的最大值符合极值I型分布(Gumbel分布),其分布函数为

式中,a为尺度参数,b为位置参数。

式中,μ为正态分布均值,σ为正态分布标准差,n为正态分布变量数。
1.3 以研究时段为寿命度量指标的构件时变可靠性
文献[16]推导了以载荷次数为寿命度量指标的构件时变可靠性公式,但海洋工程中计算时长较长,以载荷次数计算过于消耗计算力。本文将总计算时段分散为多个研究时段,每个研究时段时长为一个单位时间,假设在每一研究时段内,构件的性能不发生退化。
定义ω单位时间的时变可靠性为经过ω单位时间,构件未发生失效的概率,参考文献[16]中的方法,其可由式(11)得出:

从ω1单位时间至ω2单位时间未发生失效的概率即为

2 计算模型与讨论
2.1 计算模型参数
时域耦合分析采用由DNV开发的、内置Simo-Riflex计算模块的Sima软件进行。以内转塔式FPSO为例,平台总重为148 200 t,船长为300 m,船宽为60 m,吃水为18.75 m。系泊链采用R3级无档锚链,分布形式采用对等分布,其布置如图1所示,系泊链参数见表1。
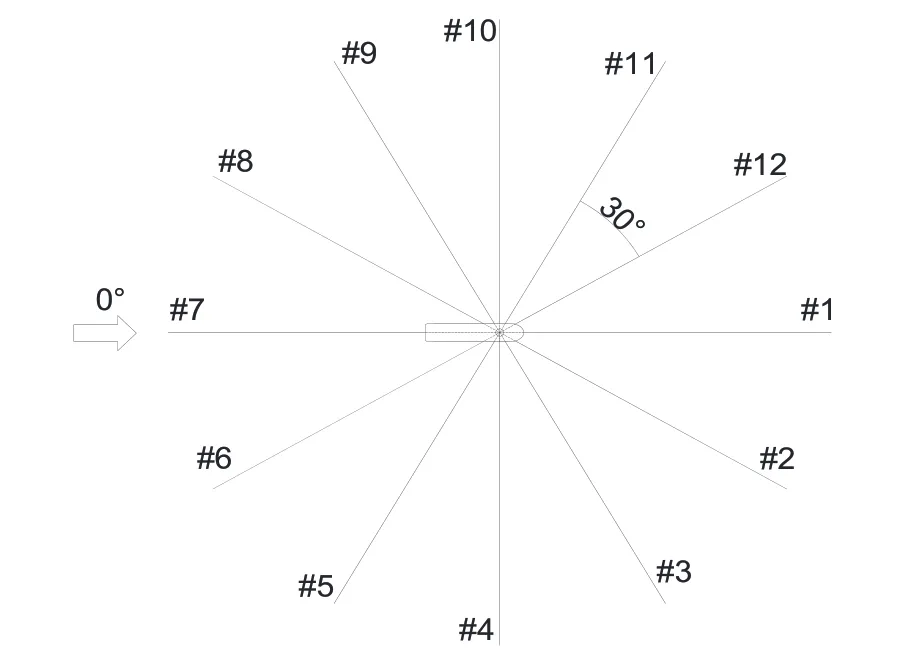
图1 系泊系统布置Fig.1 Sketch of the mooring system

表1 系泊系统主要参数Tab.1 Main particulars of mooring systems
根据Qian[17]的研究,构件的初始强度符合对数正态分布,其概率密度函数如下:

其分布参数可通过试验获得,本文取μ=15.063,σ=0.01。
风浪流环境如下:计算水深为320 m,风谱采用NPD风谱,平均风速为11.4 m/s,表层海流速度为0.5 m/s,风浪流方向均为180°。波浪采用Jonswap双波峰谱,为了数值模拟的需要,将南海某海域波浪散布图[7]根据平均波高、周期分为24种海况,如表2所示。

表2 24个短期海况Tab.2 24 short-term conditions
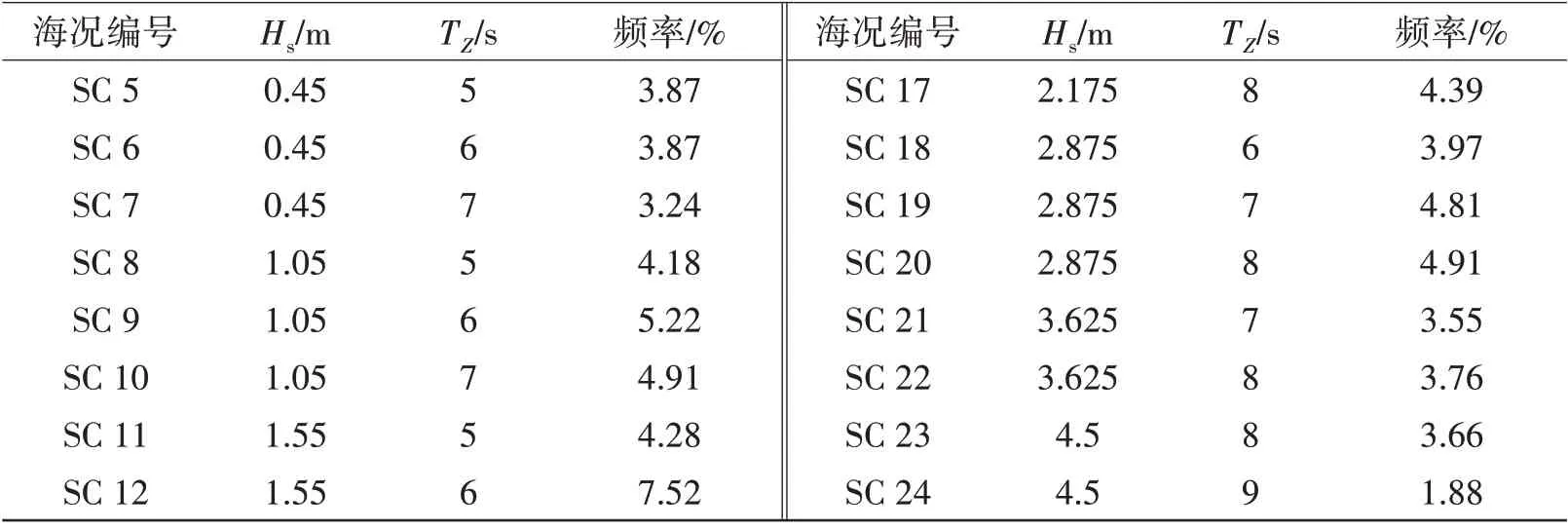
续表2
2.2 时变可靠性计算与讨论
提取水动力计算结果,取系泊链顶端节点作为关键节点,其受力时程曲线如图2所示,数值模拟计算时段时长选为10 800 s,并作为可靠性计算的单位时长。

图2 系泊链顶端张力曲线Fig.2 Time history of mooring chain top tensile force
应用雨流计数法对图2时程曲线进行计数,应用1.2节方法获取载荷的概率分布函数,初始强度的概率密度函数如式(13),不考虑检修和测试的影响由式(11)算得各系泊链顶点疲劳时变可靠性,如表3所示,以可靠性指标β表示。
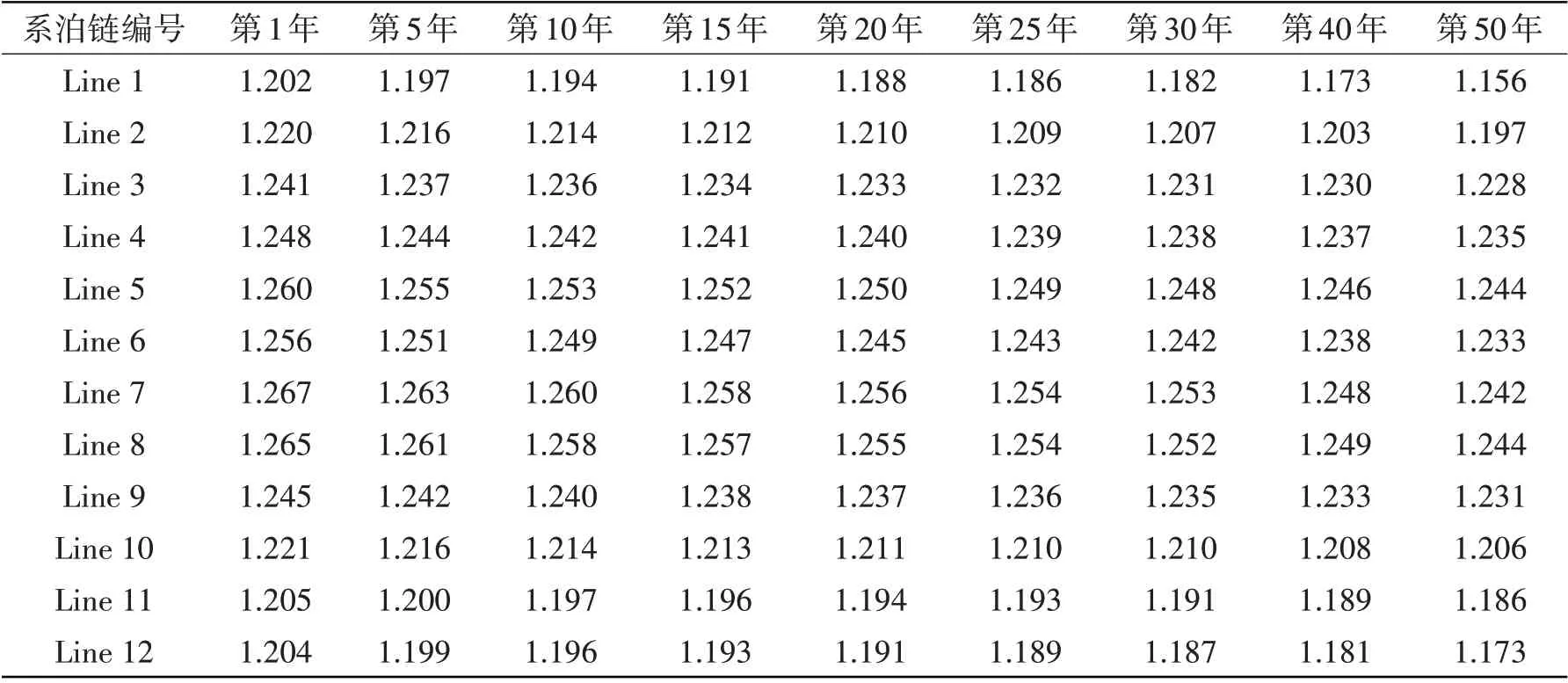
表3 各时间段的可靠性指标Tab.3 Reliability index during each period
2.3 早期测试对疲劳可靠性的影响
由表3可见,各系泊链疲劳可靠性有清晰的下降趋势,但其各时段可靠性指标极低,主要是因为未考虑平台服役前的多种测试,该结果无法被接受。而考虑到平台在正式测试进入工作状态前,通常需要在近海进行测试,则不考虑前6个月测试期内失效获得的结果更具有实际意义,各系泊链顶点疲劳时变可靠性指标如表4所示。
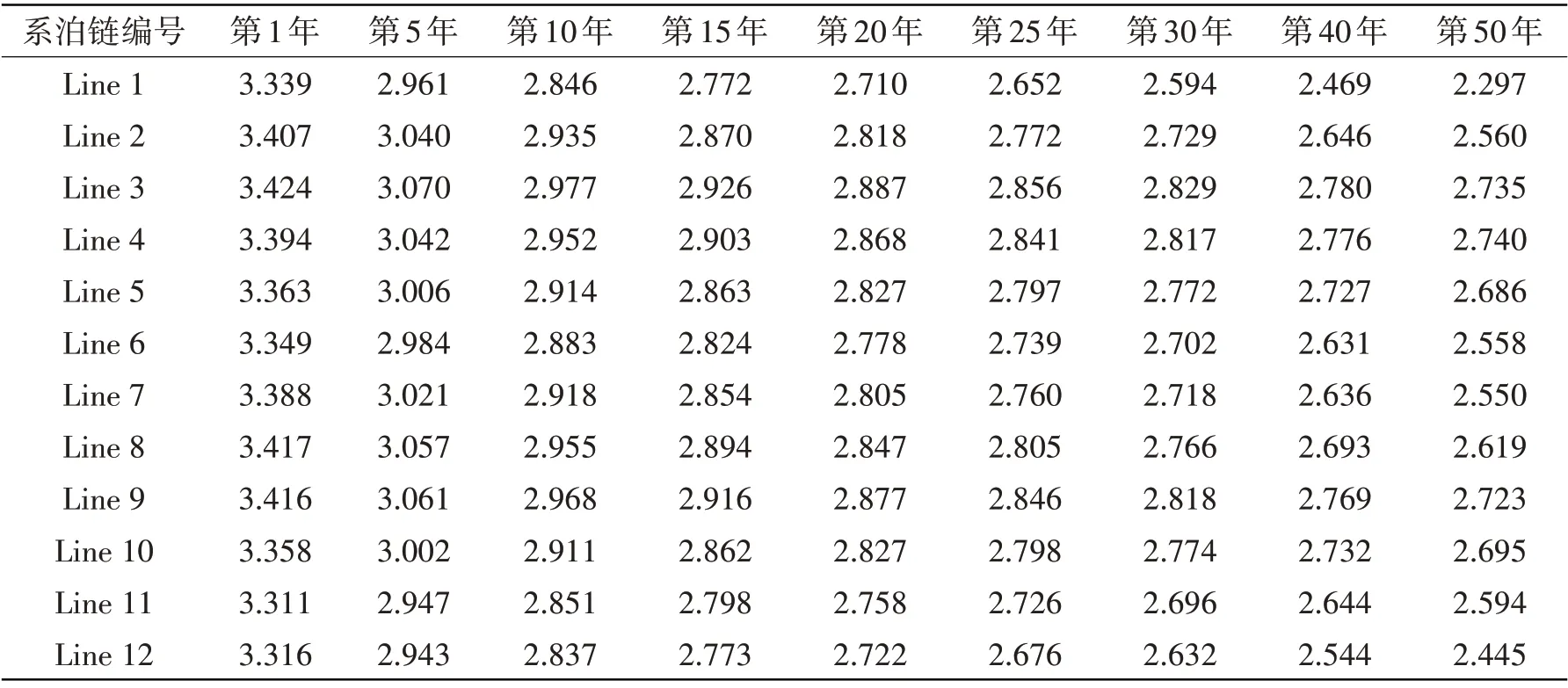
表4 考虑早期测试的各时间段的可靠性指标Tab.4 Reliability index during each period with early test
定义第i年可靠性为第i-1年未发生失效的前提下,在第i年也未发生失效的概率。选取典型的系泊链1、4、7和11,以可靠性指标β表示的时变可靠性、年可靠性变动如图3和图4所示。

图3 时变可靠性曲线Fig.3 Time-dependent reliability curves

图4 年可靠性变动曲线Fig.4 The ith-year reliability change curves
根据时变可靠性下降速率可将研究时段分为三个时期:早期(约1~3年),由于构件强度和载荷的不确定性较强,系泊链疲劳时变可靠性快速下降,此阶段需要对构件进行监控、更换不合格构件,通常为试验期;中期(约4~39年),构件强度经过早期的验证,不确定性降低,可靠性下降速率趋于平稳,此阶段运行相对安全,检修成本也较低;后期(约40年后),由于疲劳累积导致构件的剩余强度下降效果开始明显,可靠性下降速率增大,部分系泊链在短时间内疲劳可靠性快速下降,面临较大失效风险,此阶段平台趋于老龄、安全性下降,需要加强检修。文献[18]将这三种时期称为“早期失效期”、“偶然失效期”和“耗损失效期”。
另外,由于不同节点的应力时程曲线不同,导致疲劳累积的速率不同,不同系泊链的时变可靠性曲线有相交,即表示在不同时期系泊链危险程序排序有变化。
2.4 早期测试时长的影响
2.3节给出了测试期为6个月的可靠性结果,为研究测试期时长对可靠性的影响,以其设计寿命20年的可靠性为标准,获取不同测试时长下的20年可靠性指标,如表5所示。

表5 不同测试时长下的20年可靠性指标Tab.5 20-year reliability under different testing times
与表3、表4中20年可靠性数据对比,可见早期的测试可以显著提升其可靠性,同时单位增量测试时间内的提升效果随着测试时间的增大而减小,考虑测试的经济性可获取最佳测试时长。
3 结 论
本文针对海洋工程构件疲劳可靠性问题,利用Sima软件获取其在复杂海况下的动力响应,考虑构件初始强度的不确定性、载荷的不确定性、构件强度的时变性,进行了海洋工程结构疲劳时变可靠性分析,通过分析认为:
(1)海洋工程疲劳可靠性具有显著的时变性,不考虑检修的情况下,构件可靠性指标呈现下降趋势,且可靠性下降速率、系泊链危险程序排序在不同时间均有变化;
(2)根据疲劳时变可靠性下降速率可将服役期大致分为三个时期,各时期内的主要失效原因不尽相同,应针对每个时期建立不同的维护策略;
(3)早期测试可以显著增加构件设计寿命内的疲劳可靠性,但随着测试时长的增加,单位增量测试时长的提升效果减少。

