近海滑坡冲击桩体的数值模拟*

单治钢，李 阳，王 栋**，董友扣

(1.浙江华东建设工程有限公司，浙江 杭州 310006；2.中国海洋大学环境科学与工程学院，山东 青岛 266100；3.中国地质大学(武汉)海洋学院，湖北 武汉 430074)

近海工程建设中广泛采用桩基础支撑桥梁、油气平台和风机，但桩基础可能受到海底滑坡威胁：水下边坡失稳后形成的流滑体冲击滑动路线上的桩身，造成桩基乃至上部结构的破坏。近年发展起来的剪切带渐进扩展理论能够较好地描述海底土质边坡的失稳机制[1]，但追踪失稳后的流滑形态及其对下构筑物的冲击主要还是依靠模型试验与数值模拟。流滑体由土水混合组成，力学性质接近非牛顿流体[2-4]。当流滑体以较高速度冲击构筑物，法向(垂直于构筑物轴线方向)冲击压力可借助流体力学中的绕流拖曳力形式表达[5]：

(1)

式中：冲击压力p指单位投影面积上的冲击力；CD为拖曳力系数，是雷诺数Re的函数[6-7]；ρ为流滑体密度；v为冲击速度。Zakeri等[8-9]和Liu等[10-11]分别结合非牛顿流体的Herschel-Bulkley模型和幂律模型，按照式(1)给出了高速流滑体对悬浮或放置在海床表面的管线的冲击压力。当流滑体以较低速度冲击构筑物时，式(1)中CD随Re剧烈变化。如果冲击速度接近于零，更适合采用土力学中的地基基础承载力公式估算冲击压力[12]：

p=NCsu。

(2)

式中:NC为承载力系数；su为流滑体拟静力不排水抗剪强度，即流体力学中的剪应力。

为统一描述低速和高速流滑的冲击作用，Randolph和White[13]建议将流滑体对有埋深的海底管线冲击压力分解为拖曳力项和承载力项两部分：

(3)

如果流滑体自重形成的上覆压力也影响冲击压力，式(3)的承载力项可进一步细分为两部分，分别与流滑体的不排水抗剪强度和上覆压力相关[14]。但在以往的研究中，公式(3)仅被用于流滑体冲击海底管线问题，不清楚是否适合流滑体冲击桩身问题。现有的冲击桩基研究仍多采用式(1)总结冲击力[15-16]，低雷诺数时预测冲击力易导致较大误差。

本文采用计算流体力学软件Fluent，模拟不同速度的海底流滑体对桩身的冲击过程，关注低雷诺数下的冲击形态。在验证数值模型后，进行大量变动参数分析，考察影响冲击压力的主要因素，最终提出适应宽广雷诺数范围的冲击力表达式。

1 数值模型构建

1.1 问题定义

薄层滑坡厚度较小[17]，坡脚侵蚀和快速沉积诱发的近海滑坡规模不大，流滑体高度小，不考虑其自重的影响，将流滑体对桩的冲击简化为图1所示的平面应变问题。假定单桩为位置固定的完全粗糙刚体，桩径为D，在中低速冲击情况下不考虑流滑体周围水阻力的影响。采用基于有限体积法的商业软件Fluent，实施“流滑体-气”两相流模拟。

图1的计算域左边界为流体恒速进口，速度等于流滑体初始冲击速度v，用于表征流滑体到达单桩前的速度；右边界为压力出口，压力等于大气压；上下为自由滑移壁面。各边界与桩的距离必须足够远，才能保证冲击力达到稳态时不受边界影响。经过试算，确定与上下边界的距离为8D。为减弱初始计算的不稳定问题，假定流滑体与桩之间的初始距离为0.01 m，以模拟二者在计算开始时即将接触。

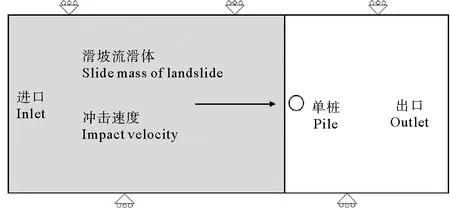
图1 流滑体冲击单桩俯视图Fig.1 Plan view of sliding impact on a pile

桩身附近的网格划分如图2所示，桩周0.2D范围为加密区，采用四边形单元，其它区域为三角形单元。桩身附近单元必须足够小才能保证计算结果的收敛性，单元大小的确定将随后讨论。采用中心差分法显式求解瞬态流动方程，为保证计算精度，规定时间增量步为：

图2 围绕桩身的细网格Fig.2 Fine mesh around the pile

(4)

式中:Lmin为单元最小长度；vmax为节点速度的最大值。

1.2 幂律流体及其雷诺数

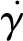
(5)

式中:n为幂律指数，当n=1时，式(5)退化为牛顿流体，高塑性无机黏土的n=0.06～0.17[18]；K为稠度系数，对于黏土质流滑体，K的范围在10～1 300 Pa·sn之间[11]。参照滑坡冲击管线问题[9]，引入名义应变速率：

(6)

对应的名义剪应力为：

(7)

牛顿流体中雷诺数定义为：

(8)

(9)

2 数值模型验证

2.1 网格敏感性

对于图1所示的流滑体冲击单桩，首先进行试算，以确定合适的网格密度。以典型幂律流体参数为例：n=0.1，K=330 Pa·s0.1，ρ=1 600 kg/m3，冲击速度v=2 m/s，桩径D=0.5 m。采用三种网格划分方案：紧邻桩身的单元尺寸分别取0.005D，0.01D和0.02D，沿径向的加密区内单元尺寸按照1.05倍的比例逐渐增大(见图2)，计算域边界上的最大单元尺寸分别为0.1D，0.2D和0.4D。得到归一化的冲击压力p/τapp随时间t的变化如图3。冲击压力达到峰值后迅速下降至稳态值，三种网格划分对应的稳态冲击压力差别在3%以内，这表明桩周围采用0.01D的单元尺寸足以消除网格敏感性。更多典型流体参数的计算也得到类似规律。为平衡计算精度与耗时，在后面的模拟中统一取桩周单元尺寸为0.01D，计算域边界上的最大单元尺寸不超过0.2D。

图3 最小单元尺寸为0.02D(绿色)，0.01D(红色)和0.005D(黑色)的模型计算结果Fig.3 Resultsofmodels with minimum element size varied 0.02D (Green),0.01D (Red)and 0.005D (Black)

2.2 流滑体冲击半埋管线问题

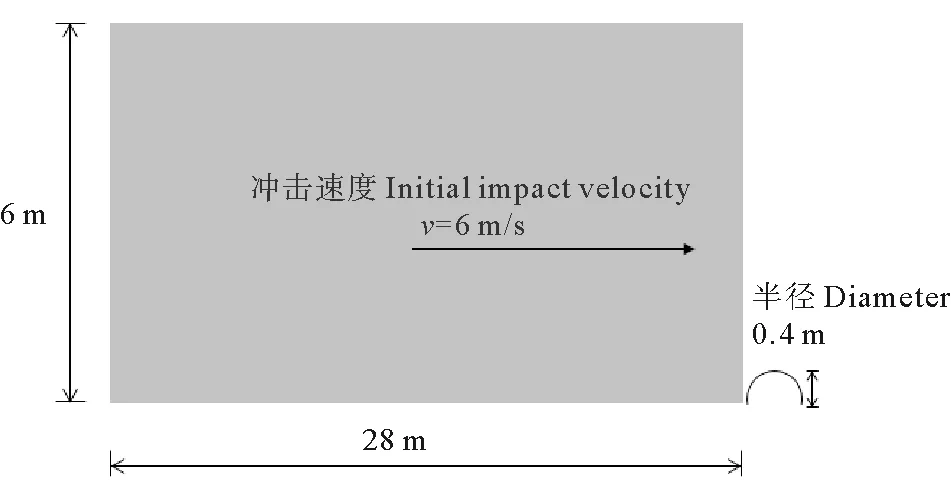
图4 滑坡冲击半埋管线问题Fig.4 Problemof semi-buried pipeline impacted by landslide

在Fluent中建立二维模型，图5比较了所得冲击压力时程曲线与文献[14]物质点法结果。两种方法差别在5%以内，初步证明了Fluent模拟非牛顿流体冲击桩身是可行的。

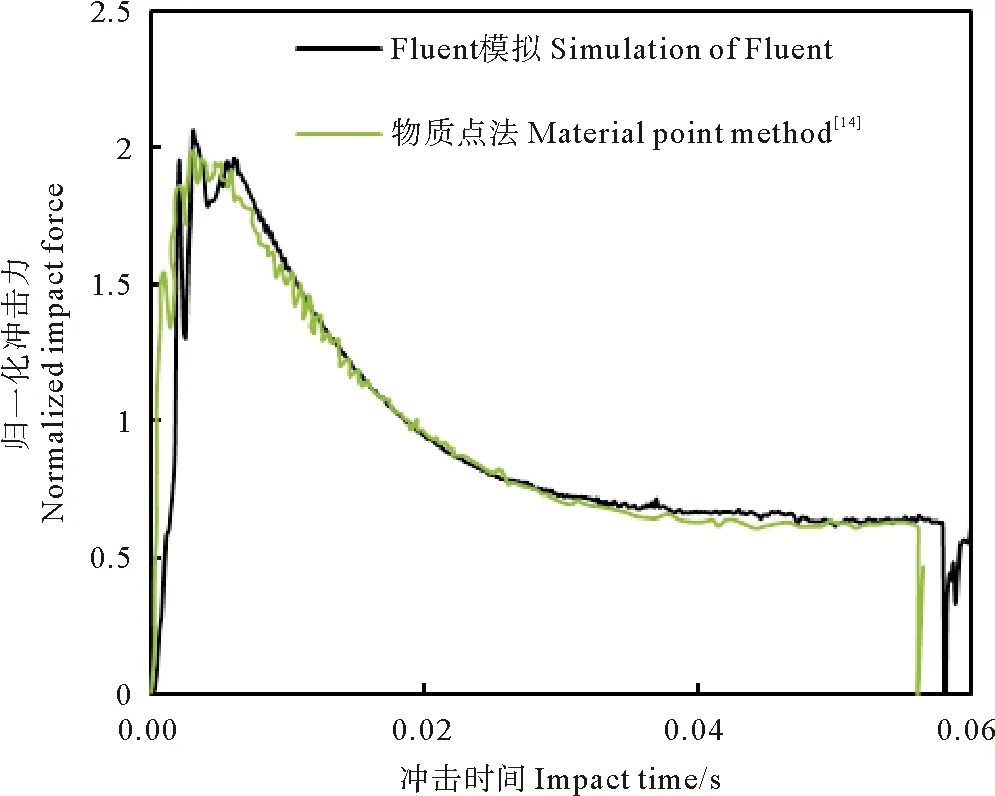
图5 Fluent与物质点法预测的冲击管线压力Fig.5 Normalised impact pressures(on the pipeline)predicted by Fluent and the material point method

3 结果和分析

3.1 冲击过程

采用建立的Fluent数值模型，考察幂律型非牛顿流滑体对桩身的冲击。如图3所示，冲击压力在0.015 s内增大到峰值(OA段)，然后由峰值迅速减小(AB段)，0.05 s之后变化速率放缓(BC段)，0.15 s后冲击压力基本达到稳定值(CD段)。各典型时刻的流滑体形态如图6所示：冲击初始阶段(t=0.02 s)，流滑体沿着桩表面流动，然后流滑体在桩后展开(t=0.035 s)，达到稳态冲击压力时(t=0.2 s)流滑体与桩背侧保持脱离。因峰值持续时间较短，对桩身威胁更大的是持续时间较长的稳态冲击，以下将集中讨论稳态冲击压力。

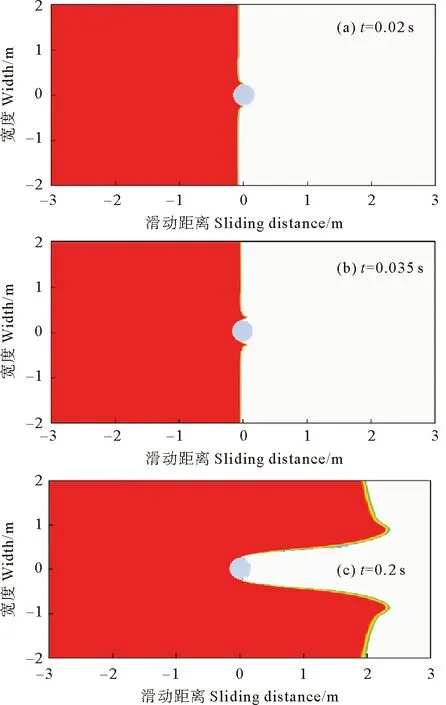
图6 冲击过程中的流滑体形态Fig.6 Morphological evolution of slide mass during impacting

3.2 变动参数分析

改变流滑体的密度和强度特性、冲击速度及桩径，实施变动参数分析，探索稳态冲击压力与上述参数之间的关系。如表1所示，根据海底滑坡的实际条件，选择ρ=1 300、1 600、1 800、2 000 kg/m3；n=0.08、0.1、0.15；模型表达式分别为τ=3100.08、τ=3300.1、和τ=3800.15Pa；v=0.1～6 m/s；D=0.5、1、2、4 m。表1中的48个算例涵盖了Re=0.1～140之间的范围。

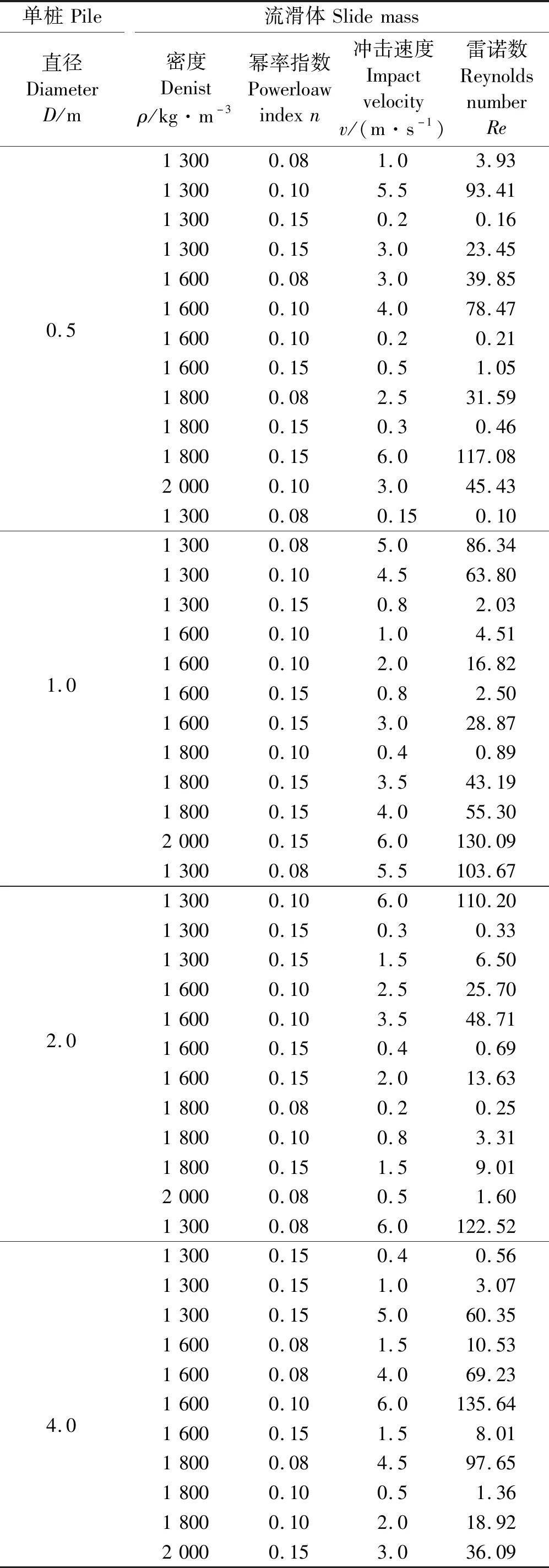
表1 计算模型参数取值Table 1 Variable parameters of calculation models

采用传统形式的单纯拖曳力公式(1)，总结表1中所有算例的Fluent模拟结果，拖曳力系数与雷诺数关系拟合为CD=0.95+12.4/Re1.1，见图7(a)、(b)更清楚地展示了低雷诺数下数值计算与拟合的CD。可以看出，当CD-Re曲线的坡度趋于平缓即Re>5时，拟合公式效果良好；但当Re<2时，如图7(b)所示，CD-Re曲线的坡度急剧变化，数值模拟与拟合公式所得结果的相对误差可能高达20%～50%，这表明低雷诺数的慢速滑动冲击问题不适合采用单纯拖曳力表达形式。

((a)宽广雷诺数范围；(b)低雷诺数范围。(a)Wide range of Reynolds numbers;(b)Low values of Reynolds numbers.)图7 采用单纯拖曳力公式总结的数值模拟结果Fig.7 Numerical results fitted as drag-force equation under

为解决低雷诺数下的冲击问题，需要同时考虑流滑体的拟静力不排水强度和惯性拖曳力。参考公式(3)，拟合表1算例的冲击压力值，见图8(a)，得到NC=7.2和CD=0.76，即

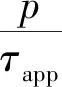
(10)

低雷诺数下的冲击压力与雷诺数关系如图8(b)所示。当Re<4时，Fluent模拟给出的p/τapp趋向于定值，也就是与公式(3)中的NC相关。图8表明，公式(10)能够合理预测Re=0.1～140范围内流滑体对桩身的冲击压力。与公式(1)相比，公式(3)不仅提供了更高的拟合精度，而且具有清晰的物理意义，低雷诺数(低流速)时的冲击力实质上就是土力学拟静力条件下的地基承载力。

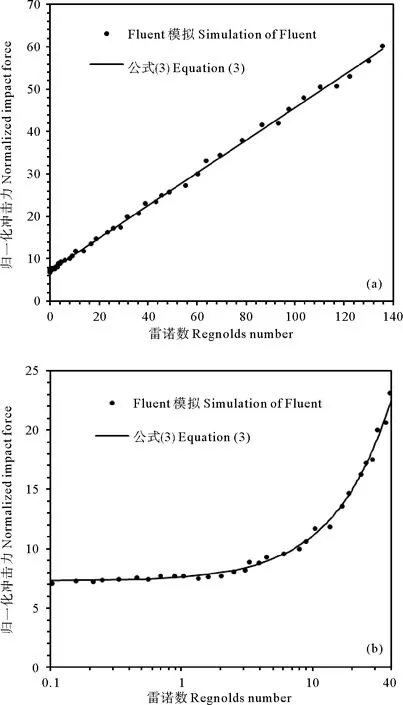
((a)宽广雷诺数范围；(b)低雷诺数范围。(a)Wide range of Reynolds numbers;(b)Low values of Reynolds numbers.)图8 归一化冲击压力与雷诺数拟合曲线Fig.8 Fitting curve of normalised impact pressure

式(10)给出了冲击压力中拖曳力项和承载力项各自的贡献，每一项所占比重与流滑体速度和名义剪应力相关。如图9所示，当Re<10时，承载力占据主导地位，尤其是Re<5时，拖曳力占比超过70%；随着Re增大，拖曳力在冲击压力中的占比增大；当Re>75时，拖曳力占比大于80%，此时可以用单纯拖曳力形式的式(1)估计冲击压力。

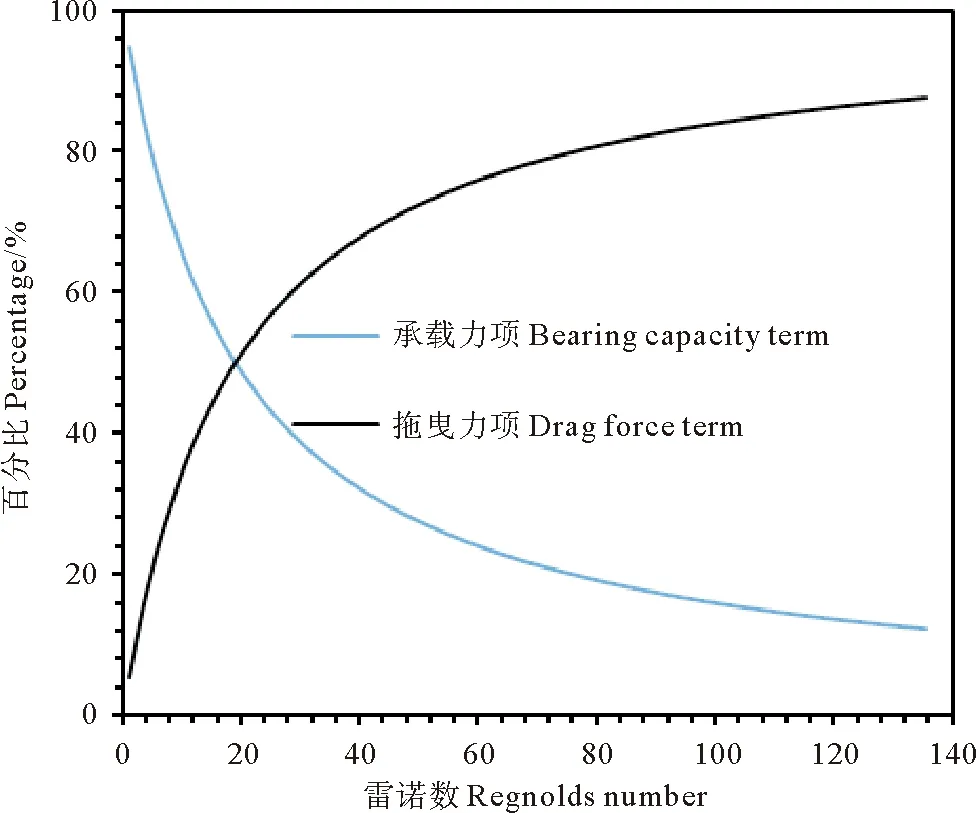
图9 承载力项和拖曳力项在归一化冲击压力中的占比Fig.9 Proportion of bearing capacity and drag force terms in normalized impact pressure

4 结语

将近海滑坡流滑体视为幂律型非牛顿流体，采用流体力学软件Fluent，探索流滑体对桩身的冲击。总结了中低雷诺数下，流滑体的变形形态和基础承受的冲击力变化趋势。给出了稳态冲击压力表达式。针对流滑体密度、粘度和冲击速度以及桩体直径等影响因素，建议采用同时包含承载力项与拖曳力项的稳态冲击压力表达式，即公式(3)，并给出相应系数，可以覆盖雷诺数在0.1～140范围内的工况。

当雷诺数较小时，桩身承受的冲击压力主要来自流滑体的不排水抗剪强度，可以通过承载力项估计冲击力。大雷诺数情况下，拖曳力项的贡献将趋于主导，拖曳力项可以代表冲击力的数量级。