函数思想在解析几何中的应用分析

◇内江师范学院数学与信息科学学院 张 静 徐小琴 吴 爽

函数思想的应用广泛，在解决数学问题中占有十分重要的地位.解析几何一直是高中数学学习的重点和难点，也是高考数学的一大热点.以高考题为例从函数构造和函数性质探究函数思想在解决解析几何问题中的应用.将函数思想渗透进解析几何问题中，不仅能够发展学生的数学思维能力，还能提高学生解决问题的能力.

解析几何是高中数学学习的重要内容之一，解决解析几何问题即通过代数方法解决几何问题.函数思想是研究高中数学问题的一种重要数学思想，穿于整个中学数学的学习，对求解解析几何问题具有重要意义.

运用函数思想方法解决数学问题，就是通过构造辅助函数，将所给问题转化成函数问题，利用函数的性质求解问题[1].以高考题为例，利用解析几何中求最值、取值范围等问题，通过引入参数构造函数，利用函数的有界性和单调性探究函数思想在解析几何中的应用.

1 构造函数

构造函数是一种重要的解题方法，能帮助学生快速找到解题思路，并快速求解问题[2].通过巧妙地构造函数，能使复杂的问题转化成熟悉而简单的问题.在解决解析几何问题的过程中，一般会通过引入变量建立相互关系.如果出现两个变量，通常把某一个变量看作自变量，另一个变量看作自变量的函数，利用函数定义建立明确的函数解析式，从而解决问题[3].常见的有三角函数、对勾函数、二次函数和高次函数等.

1.1 构造三角函数

通过巧妙地构造三角函数，并利用夹角建立等量关系，往往能简化解题步骤，有效解决解析几何问题.对于有关向量和夹角的解析几何问题，常通过构造三角函数求解.

评析：此题为向量夹角范围求解问题.在遇到求取值范围的问题时，常常会引入变量，通过构建函数，将解析几何问题转化为函数值域问题[4].由于需求的夹角范围，因此，容易联想到向量的夹角公式，从而将解析几何问题转化为三角函数问题.根据向量的夹角公式利用余弦表示两向量的夹角，由题目已知条件易知其值域，于是，直接利用反三角函数知识得出结果.

1.2 构造对勾函数

求解解析几何大题时，分式函数通常和圆锥曲线最值问题结伴出现[5].在研究解析几何的最值问题，遇到分式函数时，通常构造形如的对勾函数求解问题.对勾函数是高中数学阶段中一种常见而又特殊的函数，利用对勾函数的图象和性质解决有关问题，简捷而准确.

评析：第(Ⅱ)(ⅱ)问需求出三角形面积的最大值.由(ⅰ)容易写出三角形面积关于直线斜率的函数表达式，于是将问题转化为函数的最大值问题.解决问题的关键在于构造函数求出函数表达式的最大值.通过构造形如的对勾函数，并利用换元法，求出函数的定义域，再构造一次对勾函数，于是根据对勾函数的性质求解最值.

2 利用函数性质

解析几何问题常利用函数法求解，通过构造函数，结合函数的性质解决问题，往往能够降低解题难度.对于解析几何的最值和取值范围等问题，许多学生选择放弃，在解决这类问题时，这时如果考虑利用函数的有界性和单调性，往往能够有效解决问题.

2.1 利用函数有界性

在利用函数的有界性解决问题时，无论是构造如例1、例2的三角函数和分式函数，还是其他各种函数，都需要明确函数解析式的定义域，然后才能利用函数的有界性求解问题.

评析：第(Ⅱ)问需要求四边形面积的最大值.根据题目条件，观察几何图形的特征容易写出四边形面积关于引入参数的函数表达式，于是将问题转化为函数的最大值问题.由于四边形面积中含有根式需满足，所以由 的取值范围根据函数的有界性，容易得出四边形面积的最大值.

2.2 利用函数单调性

函数的单调性常用来求解有关取值范围和最值的解析几何问题.利用函数的单调性求解解析几何问题时，常用的方法有配方法、求导法.对于一元二次函数常用配方法，对于高次函数常用求导法，通过配方法和求导法利用函数的单调性求解.

3 借助函数图象的对称性

函数图象是函数的一种表达形式，是探索解题方法，获得问题结果的重要途径[7].在解析几何问题中，常常包含对图形对称性的考查.在解决问题时，通过对函数图象的对称性进行探究，有助于加深理解，在解题时起到事半功倍的效果[8].

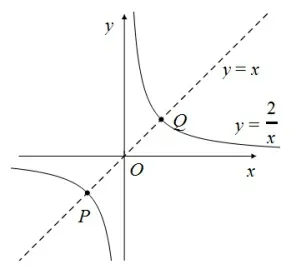
评析：题为求线段长度的最小值问题.在求解问题的过程中，根据函数解析式作出图形，将数与形相结合，充分利用了函数图象的对称性.在解决一些问题时，运用函数图象，通过形的直观往往能够避免复杂的运算过程，快速简洁的解决问题，解法具有明显的优势[9].