多无人机协同侦察路径规划研究∗
黄 辉 年福耿
(海军士官学校 蚌埠 233012)
1 引言
红蓝双方的实兵、实地、实战的对抗演习,现已成为我军常态化的练兵活动。在演习的过程中,需要实时掌握红蓝双方对抗的情势,拟通过无人机携带高分摄像机对演习区域进行实时记录拍摄。据相关资料可知,无人机为实地拍摄专用,其平均飞行速度60km∕h,飞行转弯半径不小于50m,飞行高度不超过海拔2100m,摄像机对地的辐射角度为120°,飞行中与其他地物(山体、地面、树木、建筑物等)之间的安全距离不小于50m。
2 问题的提出
现已获知某演习区域的数字高程数据,假设某一时刻有三架无人机同时从边界(0,30km)处进入该区域,欲完成对该区域的侦察。考虑到战场实际和飞机性能,三架无人机的飞行路线和各自拍摄区域,需要进行科学合理的规划,使其完成任务的时间尽可能短、作业时间尽量均衡、且拍摄覆盖率尽可能高。
3 无人机作业量分配
本文首先利用演习区域高程数据画出山体的等高线图,并计算出2000m以下区域的面积,海拔高于2000m的山体,大致分布在三个区域。由于无人机只需对2000m以下区域进行拍摄,且三架飞机作业量尽量均衡,因此本文利用EXCEL计算出2000m以下区域的面积,并对其三等分,每一块面积376.835km2,由于无人机拍摄过程中探测的面状区域大多处理为矩形,且飞行过程中一般采用“弓字形”路线[3],于是本文对分割好的区域进行微调,将拍摄区域内不规则的山体用小矩形区域进行切割,使之符合无人机工作原理。

图1 区域划分
调整后计算得出无人机实际需要拍摄的面积1号区域357.635km2,2号区域350.595km2,3号区域339.715km2,比较接近。
4 拍摄区域内路径规划
取三个拍摄区域的平均海拔1750m为基准地面高度,无人机飞行高度固定为2100m,摄像机对地幅角120°,利用三角函数和面积公式计算出无人机点状拍摄面积为0.68km2。

图2 无人机点状拍摄工作图
所以无人机飞行时在地面形成的带状拍摄区域幅宽为0.8km。
考虑要保证拍摄区域覆盖率高,可以使用幅宽为0.8km的带状区域覆盖拍摄区域,同时可对拍摄区域内的路径进行规划。由于幅宽为0.8km远大于50m的转弯半径限制,无人机只需在距离区域边界0.4km处转弯即可。

图3 无人机飞行时拍摄的带状区域示意图

图4 无人机转弯示意图
察阅资料可知,无人机飞入面状目标区域内的切入点的位置因航线条数奇偶性的不同而有两种情形:当航线条数为偶数时,切入点和退出点在矩形区域的同一条边上;当航线条数为奇数时,切入点和退出点分别落在矩形区域的一对对边上[1]。

图5 面状区域内无人机航线规划示意图
本文以3号区域为例,根据相关数据可计算出3号区域航线条数为奇数,按照“弓字型”飞行,如从左上端切入,那么必然从右下端飞出,由于无人机拐弯时要多花费些时间来切入下一条航线,因此,在面状目标内部进行航线规划时,要遵循拐弯次数尽量少的原则。根据这个原则,取矩形较长边的方向为航线方向,然后再根据航线间隔,在该区域布设航线,见图6。

图6 途中无向图构造示意图
5 起飞点到拍摄区域的途中最短路径规划
由于问题要求三架飞机同时从边界(0,30km)处进入各自探测区域,其中两架飞机远离侦察区域,需要对飞机的途中路径进行规划。本文以TSP模型为基础,进行调整提出适应本文使用的途中最短路径规划模型,设wij是(i,j)边的权值,即i与j之间的距离,则有如下模型:

该模型使用需要构造无向图,以2号区域为例,在无人机由(0,30km)处(即A点)起飞到2号区域的拍摄途中,选取可能存在的路线转折点(即2000m等高线上点)作为图的节点,连接节点,就得到了2号区域的路径无向图(见图7)。

图7 “1号区域”无人机航线规划示意图
再利用Matlab编程可计算出途中路径规划结果,结合上一问中的区域内规划的路径,如图8~9所示,可以得到最终三架飞机的侦察路径。
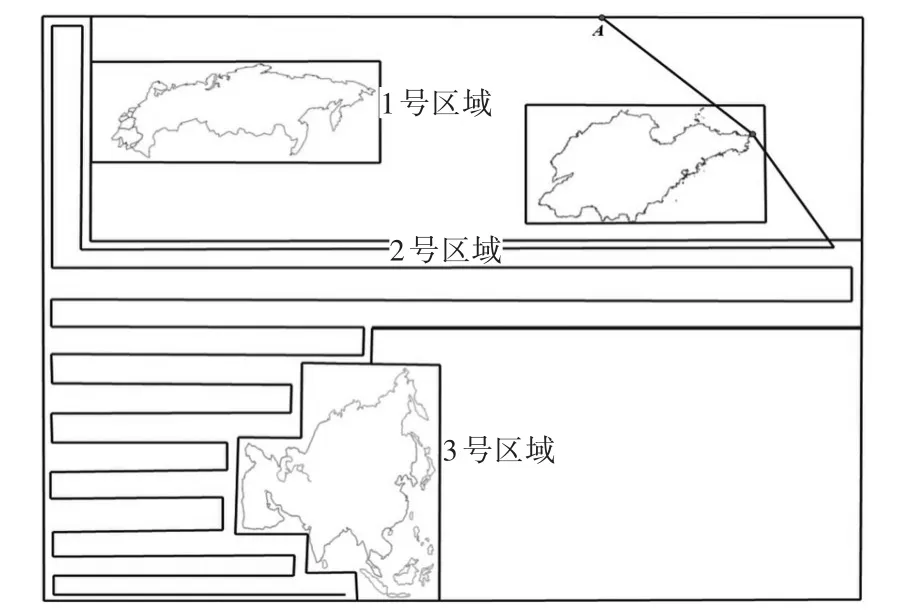
图8 “2号区域”内无人机航线规划示意图

图9 “3号区域”内无人机航线规划示意图
三架无人机的飞行时间、覆盖面积、覆盖率见表1。

表1 三架无人机拍摄规划总表
由表中数据可见三架无人机作业量、飞行时间、覆盖率都比较接近,且效率较高。
6 结语
多无人机协同路径规划是比较复杂的问题,本文仅从工作量均衡、路径最优等角度出发对多无人机侦查区域进行划分从而实现研究目标,整个研究背景较为简单,与客观环境复杂程度相比尚有不足,有待后续进一步完善研究。

