基于转向角的变化分析转向力矩波动方法

皮秋生

（上海世科嘉车辆技术研发有限公司，上海 201700）

引言

传统的分析力矩波动方式是通过计算转速或力矩的变化来获取。但在实车的测试中，转向力矩包含了EPS的力矩补偿，转向传动系的摩擦，路面负载输入的不稳定等因素，导致力矩失真，不能真正的体现车辆的设计力矩波动是否合理。而转向角的变化不受上述因素的影响，同理转向角传动比也可以排除上述干扰。本文介绍了从转向角的变化来分析研究转向力矩波动。

1 非等速万向连接传动理论

如图1所示，为单万向节结构。令轴Ⅰ，轴Ⅱ分别绕各自的旋转轴转动，则与两轴垂直且相互垂直的十字轴和对应的节叉的相交点必定绕一球体的表面作圆周运动。

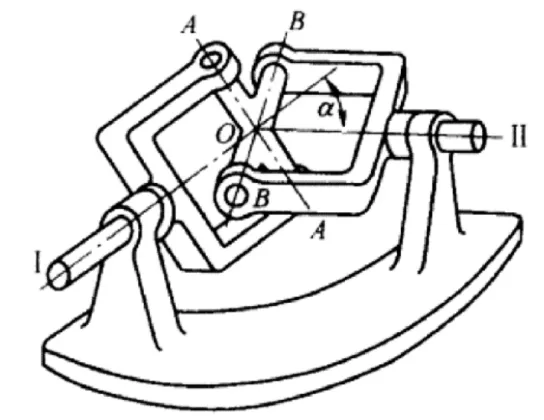
图1 单万向节传动连接[1]

存在于两轴转动之间的关系可用球面三角推导出来[2]。设轴Ⅰ转动角度为φ1，则轴Ⅱ转动角度为φ2，则有两角度之间的关系式为[3]：

或

2 转向传动转角的变化及波动分析

根据相关分析，双联式万向节，只有在输入、输出轴平行或相交时，并且二者在空间的位置固定不变时，才能获得匀速特性。对于转向传动机构，受制于整车布置的限制，上述匀速条件基本不能保证，常见的转向系统布置如图2所示。

图2 常见转向系统布置

转向传动系统简化形式如下图3所示。

图3 转向传动示意图

转向传动在中间轴l2的垂直面上的投影如图4所示（管柱下节叉与面P1重合，即0转角）。

图4 转向传递投影示意图

设管柱、中间轴、转向器输入轴转角分别为φ1、φ2、φ3，方向为驾驶员视角顺时针为正。管柱-中间轴平面P1与中间轴-输入轴平面P2的夹角τ为驾驶员视角P1顺时针转到P2的角度。中间轴上节叉与下节叉夹角（即中间轴相位角）ψ为上节叉顺时针转到下节叉的角度。

根据管柱方向盘输入转角φ1，计算中间轴上节叉输出转角可根据式（2）求得：

对中间轴、转向器输入轴组成的单万向节，当管柱下节叉转角为0时，根据图4可知，中间轴下节叉作为主动轴，其起始角度为λ，节叉0位为节叉两端轴所形成的平面[1]，根据角度关系，计算式为：

因此，当管柱转角为φ1时，中间轴下节叉（第二万向节的主动轴）初始角度为：

根据式（3），转向器输入轴的转角为：

其中：

实际管柱设计时，输入轴管柱节叉与方向盘12点方向的夹角为φ0（驾驶员视线方向，节叉左转至12点方向为正）。管柱-中间轴平面P1与12点方向夹角为△（驾驶员视线方向，管柱-中间轴平面P1右转至12点方向为正），如图5所示。

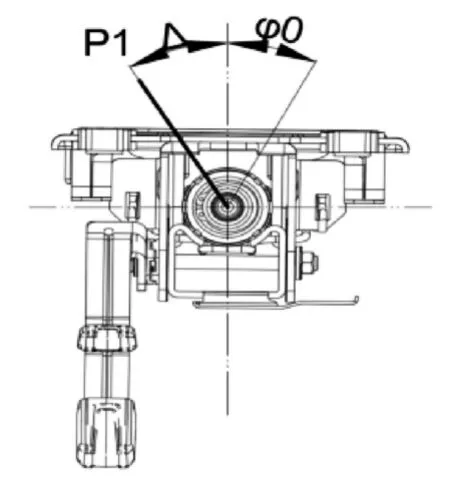
图5 管柱初始相位示意图

则初始输入轴转角满足如下关系：

同理，利用式(6)，可计算出初始输出轴转角φ3（0）。

在计算时，可调整φ0角，即调整输入轴的初始相位角，使力矩波动在方向盘0角度时处于波峰或波谷位置。

考虑转向器的线角传动ic，mm/r，则转向器的齿条位移为：

转向器齿条行程与转向车轮转角之间的关系随不同车型的转向梯形呈现不同的微小的非线性关系。设平均单位齿条行程对应的转向轮转角为is，°/mm，则管柱旋转φ1时，转向车轮的角度为：

瞬时转向角传动比定义为：

根据力矩波动定义和功率守恒原理，有如下式成立。

转速为单位时间t内转过的转角，即：

式（12）变为：

式中：

φ1(n)、φ1(n-1)、i(n)、i(n-1)分别为测试时第n点和第n-1点的输入轴转角和瞬时传动比。

3 应用实例

为检验上述转向力矩波动校核方法，以国内某车型为例，按上述方法来计算如下：

表1 某车型转向参数

根据式（11），转向瞬时角传动比i（未考虑转向梯形的非线性关系）与φ1关系曲线如下图6所示：

图6 输入轴转角-转向角传动比关系

根据式（14），利用转向角传动比变化得出力矩波动曲线如下图7所示，最大3%。

图7 输入轴转角-转向力矩波动关系

转向传动比实测数据如下图8所示，波动率为2.8%。

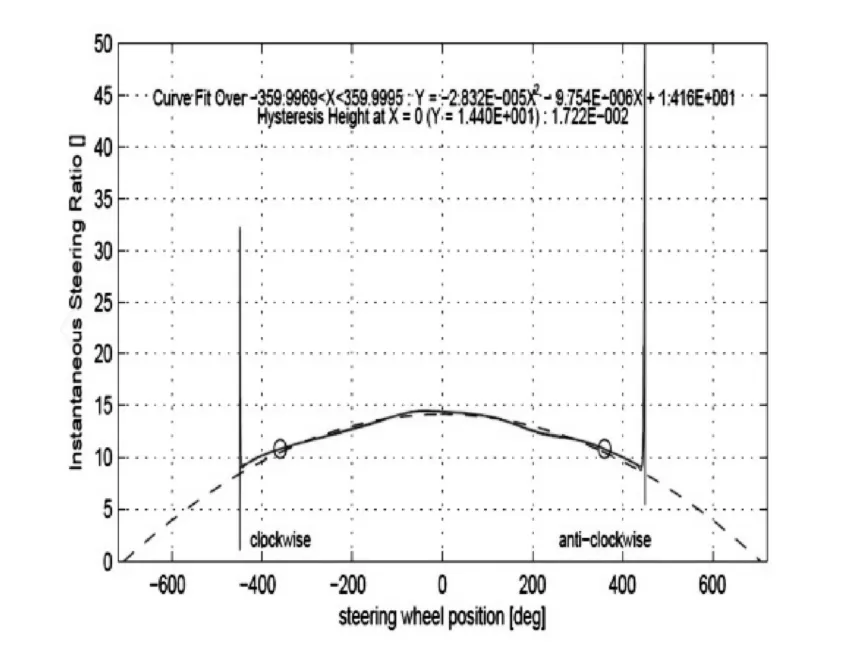
图8 转向传动比实测图

由上分析可知，前述转向力矩波动计算结果有较小的误差，方式有效。

4 结论

为降低转向力矩波动，在转向设计布置初期，转向硬点的布置应尽量减小夹角α1、α2或|α1-α2|。而为了实测力矩波动时排除EPS助力及摩擦的干扰，可以采用计算转向角传动比变化的方式分析力矩波动。