基于分段加Nuttall窗插值FFT的电压暂降检测方法

徐 勇，向运琨，曾 麟，何 哲

(国网湖南综合能源服务有限公司，湖南 长沙 410007)

0 引言

电压暂降是电力系统中发生频次较多、影响较大的一类电能质量问题，会导致电力系统中敏感性用电设备的非正常工作，严重时甚至造成设备发生故障而停止运行，给用户带来巨大的经济损失[1-3]。此外，随着电力电子技术的不断更新，尤其是数字自动控制技术的广泛使用，电压暂降造成的相关问题也愈加突出[4-5]。相关统计数据表明，有80%以上的电能质量问题都是由电压暂降引起的[6]。因此，电压暂降问题越来越受到相关部门和研究人员的关注和重视[7]。

国内外学者在电压暂降检测方面作了大量的研究工作，分别提出了均方根值法、峰值电压法、基波分量法、小波变换法和d-q变换法等[8-10]。均方根值法、峰值电压法和基波分量法等传统电压暂降检测方法在暂降持续时间检测时存在较大误差，且无法给出骤降发生时可能出现的相位跳变信息。小波变换法虽然能够有效提取电压暂降的相关特征量，但其存在母函数选择复杂、抗噪性差和计算量大等问题。d-q变换法通过d-q变换实现对称三相电压瞬时均方根值的求取，从而实现暂降特征量的获取。但在检测前需要进行相应的相位延迟，导致额外增加系统的响应时间。

为此，本文提出了一种基于分段加Nuttall窗插值快速傅里叶变换(fast Fourier transform，FFT)的电压暂降检测方法。该方法首先通过对电压暂降信号进行求导和平方和运算来划分电压信号稳定区间，并得到暂降起止时刻和持续时间，而后对稳定区间内的电压信号进行加Nuttall窗插值FFT运算来得到电压暂降的暂降幅值和相位跳变等特征量，从而实现电压暂降特征量的快速、准确检测。

1 电压暂降的基本概念

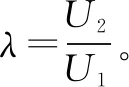
在三相系统里，一般假设最先受电压暂降扰动的某一相的均方根电压值低于暂降起始阈值的时刻，为暂降起始时刻；在各相均方根电压值都恢复到正常供电时均方根电压值的时刻，为该电压暂降的结束时刻。

2 电压暂降检测方法

2.1 暂降起止时刻和持续时间的检测

设电压暂降稳定区间内的电压信号模型为：

s(t)=Acos(2πft+φ)

(1)

式中：A为信号的幅值；f为信号的频率；φ为信号的初相角。

对式(1)求一阶导数，可得：

s′(t)=-A×2πfsin(2πft+φ)

(2)

综合式(1)和式(2)，可得稳定区间内电压信号的幅值为：

(3)

对式(3)进行离散化处理，可得：

(4)

式中：fs为采样频率；s(n)为信号采样值，n=1,2,…,N-1。

由于电压暂降信号在暂降开始时刻和结束时刻的导数不连续，即存在第一类间断点，使得计算出的幅值会远大于实际幅值。通过合理设置幅值检测阈值，即可很好地确定电压暂降起始、终止时刻，并可得到电压暂降的持续时间。考虑到实际电网谐波和噪声的影响，本文将幅值检测阈值定义为2.5。

2.2 暂降幅值和相位跳变的检测

FFT具有计算效率高、易于嵌入式实现等优点，被广泛应用于电力系统分析中。但在非同步采样条件下，FFT会不可避免地引起信号的频谱泄漏和栅栏效应，使得电力系统相关参数检测的准确度往往不高。为此，本文采用加Nuttall窗插值FFT来有效抑制暂降稳定区间电压信号的频谱泄漏和栅栏效应，进而准确获取电压暂降的暂降幅值和相位跳变等特征量。

2.2.1 Nuttall窗函数特性

Nuttall窗为一组余弦组合窗，其时域表达式为：

(5)

典型Nuttall窗函数的系数如表1所示。其中：Nuttall-I表示4项3阶Nuttall窗函数；Nuttall-II表示4项1阶Nuttall窗函数；Nuttall-III表示3项最小旁瓣Nuttall窗函数；Nuttall-IV表示4项最小旁瓣Nuttall窗函数。

表1 典型Nuttall窗函数的系数

表1中不同系数Nuttall窗函数所对应的幅频特性曲线如图1所示。其中，窗函数长度为N=64。

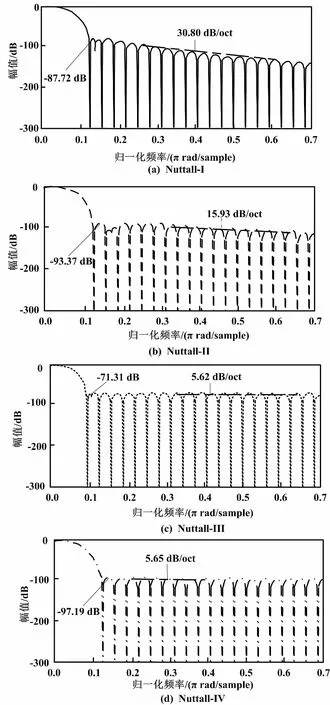
图1 不同系数Nuttall窗函数所对应的幅频特性曲线

由图1可知，Nuttall-III和Nuttall-IV的旁瓣峰值电平分别为71.31 dB和97.19 dB，两者的旁瓣衰减速率分别为5.62 dB/oct和5.65 dB/oct。Nuttall-II的旁瓣峰值电平为93.37 dB，旁瓣衰减速率为15.93 dB/oct。Nuttall-I的旁瓣峰值电平(82.72 dB)要小于Nuttall-II，但其旁瓣衰减速率(30.8 dB/oct)要明显优于Nuttall-II，从而更好地抑制旁瓣泄漏。从图1可见，在这4个Nuttall窗函数中，Nuttall-II的主瓣适中、旁瓣衰减速率最快，故本文选择Nuttall-II窗函数作为加窗插值的窗函数。

2.2.2 加Nuttall窗函数插值FFT获取暂降幅值和相位跳变

在确定电压暂降的起止时刻之后，即可划分相应的暂降稳定区间。通过在电压稳定区间采用加Nuttall窗函数插值FFT来获得相应区间的电压幅值和相位信息，进而得到暂降幅值和相位跳变等特征量。

设采样后的电压信号为x(n)。考虑到实际电网环境往往伴有谐波存在，故有：

(6)

式中：H为谐波的最大阶数；N为信号的采样长度；fh为第h次谐波的频率；fs为采样率；Ah和φh分别为第h次谐波的幅值和初相位。

对式(6)采用Nuttall-II窗函数进行加权并进行离散时间傅里叶变换(discrete time Fourier transform，DTFT),可得：

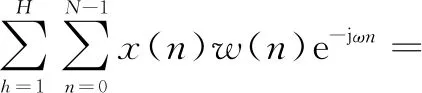
(7)

式中：W(ω)为Nuttall-II窗函数的频谱函数;ωh为第h次谐波的数字角频率；w(n)为Nuttall-I型窗的时域离散表达式。

式(7)对应的离散傅里叶变换(discrete Fourier transform，DFT)为：

(8)

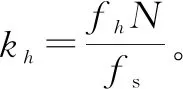
在非同步采样条件下，kh为一个非整数。故设kh1和kh2(kh1≤kh≤kh2=kh1+1)分别为kh附近的2个局部最大值谱线。为求得kh，先定义一对称系数α∈[-0.5,0.5]。由于kh1≤kh≤kh2=kh1+1，则有kh=kh1+α+0.5。再定义另一系数β如下：

(9)

因直接求解式(9)的反函数过于复杂，本文结合kh附近的2个局部最大值谱线并采用最小二乘法来拟合α。具体步骤如下。

①α在区间[-0.5,0.5]内按照步进0.01取101个点，分别计为αi(i=1,2,…,101)。

②根据暂降特征量的检测精度要求，选取合适的拟合多项式阶数L。通常取L为5或7，即可满足要求。本文取L=7。

③通过αi、βi以及拟合阶数L，可求得拟合多项式系数ql(l=1,2,…,L)。

④因β是α的偶函数，故拟合多项式的偶数项均为零，即:

α=q1β+q3β3+…+qLβL

(10)

由上述步骤可得，α和β采用Nuttall窗函数的7阶拟合多项式为：

α=2.954 9β+0.176 8β3+0.089 8β5+

0.056 8β7

(11)

在得到α值后，稳定区间电压信号x(n)的各次谐波频率为：

(12)

各次谐波的幅值Ah可采用式(13)进行计算：

(13)

当N值较大时，可简化为：

(14)

同理，ζ(α)亦可采用最小二乘拟合多项式逼近，因此可改写为：

(15)

式中：α为拟合式自变量；cj为拟合式系数；J为拟合多项式的最高阶数。

Ah是α的偶函数，故ζ(α)的6阶拟合多项式为：

ζ(α)=3.209 8+0.919 2α2+0.141 9α4+

0.016 4α6

(16)

将式(16)代入式(14)，即可得到h次谐波的幅值Ah。

此外，第h次谐波的相位为：

(17)

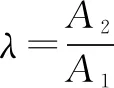
2.3 电压暂降特征量检测流程

图2为基于分段加Nuttall窗插值FFT的电压暂降特征量检测方法流程图。

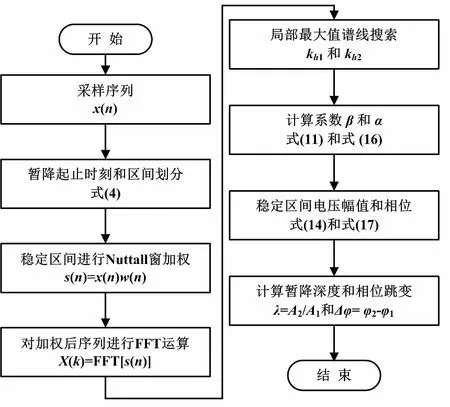
图2 基于分段加Nuttall窗插值FFT的电压暂降特征量检测方法流程图

本文所提基于分段加Nuttall窗插值FFT的电压暂降特征量检测方法的主要步骤如下。

①对采样后的被测电压信号x(n)进行求导、求和运算，得到暂降起止时刻和持续时间。

②依据暂降起止时刻划分电压暂降稳定持续区间，对稳定持续区间的采样信号进行加Nuttall窗插值FFT运算，得到基波附近的2个局部最大值谱线(kh1和kh2)。

③由基波附近2个局部最大值谱线(kh1和kh2)，可得拟合多项式(11)和式(16)的值。

④将拟合多项式的值分别代入式(14)和式(17)，可得电压暂降稳定区间的幅值和相位。

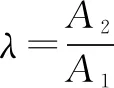
3 仿真试验与实际测试

本节分别在同时发生幅值暂降和相位跳变、谐波影响以及白噪声影响等这3种情况下，采用本文方法对电压暂降信号进行检测。仿真时采样频率为6.4 kHz，采样长度为10个周波。

3.1 同时发生幅值暂降和相位跳变时的电压暂降检测

设电力系统供电电压U0为220 V、基波频率f0为50 Hz，则同时存在幅值暂降和相位跳变时的电压暂降仿真信号表达式为:

(18)

式中：t1为暂降起始时刻,t1=0.04 s；t2为暂降结束时刻,t2=0.12 s；λ为暂降深度,λ=0.8；φ为相位跳变量,φ=-30°。

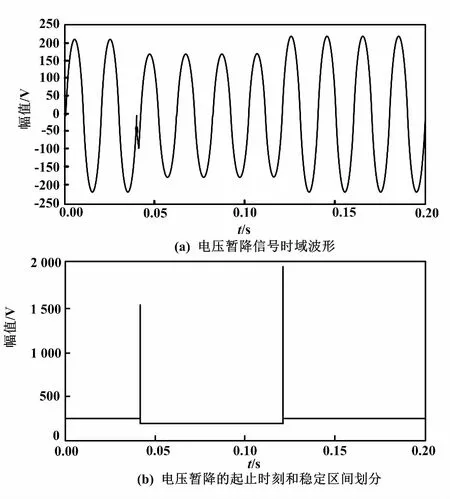
图3 基于分段加Nuttall窗插值FFT的起止时刻和持续时间检测结果(Ⅰ)

3.2 谐波影响下的电压暂降检测

随着大量的非线性和冲击性负荷在电力系统的广泛使用，对实际电网的电能质量造成了严重的污染，引入了大量的谐波成分。为此，在电压暂降的基础上叠加谐波成分，具体表达式为：

(19)

式中：U0为电网供电电压，220 V；f0为基波频率,50 Hz；H为最高的谐波阶次；hi为各次谐波幅值系数,0.05≤hi≤0.3(i=2,3,…,H)；λ为暂降深度,取0.8；φ为相位跳变量,取-60°。

考虑到实际电力系统中第3、第5、第7次谐波的含量较多，故设定各次谐波的幅值分别为h3=0.15、h5=0.1、h7=0.05。含谐波分量的电压暂降信号基于分段加Nuttall窗插值FFT的起止时刻和持续时间检测结果(Ⅱ)如图4所示。由图4(a)可知，由于受到谐波的干扰，暂降信号的波形已经产生了明显的畸变。由图4(b)可知，信号在t′1=0.039 7 s时发生了幅值瞬时下降，并在t′2=0.119 8 s时恢复正常幅值，电压暂降持续时间为td=t′2-t′1=0.080 1 s。同理，对划分好的3个暂降幅稳定区间分别进行加Nuttall窗插值FFT运算，可以得到相应基波幅值，分别为219.994 4 V、176.000 1 V和220.000 0 V，基波相位分别为-1.582 4°、-62.812 3°和-0.000 0°。所以，暂降持续期间的暂降幅值为正常电压幅值的80.00%，即暂降深度为0.8；电压信号波形在暂降发生和结束时存在明显的相位跳变，相位跳变量分别为-61.229 9°和62.812 3°。

图4 基于分段加Nuttall窗插值FFT的起止时刻和持续时间检测结果(Ⅱ)

3.3 白噪声影响下的电压暂降检测

为检验方法的鲁棒性，在上述仿真信号的基础上叠加一定信噪比(signal to noise ratio，SNR)的高斯白噪声。设置信噪比变化范围为30～80 dB，步进量为10 dB。电压暂降信号的暂降起止时刻(持续时间)、暂降深度以及相位跳变量等其他参数与式(19)一致。考虑到噪声的统计特性，每个信噪比条件下的测试样本个数选为3 000个。

本文方法在不同信噪比影响下检测结果的平均相对误差如表2所示。由表2可知，随着测试样本的信噪比逐渐减小，电压暂降3个特征向量检测所得相对误差变化不大，表现出极好的鲁棒性。暂降幅值检测的最大相对误差仅为0.000 3%。暂降持续时间检测的最大相对误差仅为0.195 3%。相位跳变检测的相对误差较大，其最大相对误差为9.370 3%。

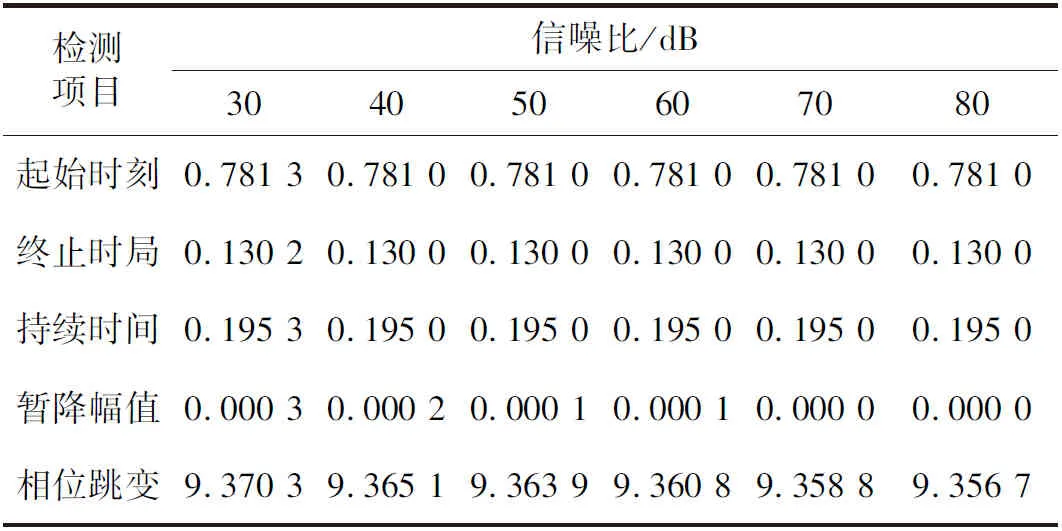
表2 不同信噪比影响下检测结果的平均相对误差

3.4 与其他检测方法对比

为进一步验证所提方法的准确性和有效性，将本文所得检测结果分别与改进d-q变换检测方法[13]、改进S变换检测方法[14-15]的检测结果进行对比。设置电网供电电压U0为220 V，基波频率f0为50 Hz，暂降信号起始时间为0.06 s，截止时间为0.12 s，暂降深度λ为0.4，相位跳变量为-30°，采样速率均为6.4 kHz，采样长度为1 280个点。不同方法所得电压暂降特征量的检测结果如表3所示。

表3 不同方法所得电压暂降特征量的检测结果

由表3可知，采用d-q变换检测方法仅能检测出暂降的起止时刻，无法获得暂降深度和相位跳变等信息；采用改进S变换能够获得电压暂降的起止时刻、暂降深度和相位跳变等信息，但准确度不如本文方法，且运算量较大；采用本文方法所得检测结果在3种检测方法中准确度最高，所得暂降起始时刻为0.059 7 s、结束时刻为0.119 8 s、暂降深度为40.00%、相位跳变量为30.816°。

3.5 实际测试与应用

在理论分析与仿真试验的基础上，设计了基于模数转换器(analog to digital converter，ADC)+数字信号处理器(digital signal processor，DSP)架构的电压暂降特征量硬件测试平台。测试平台结构如图6所示。图6中：ADC芯片采用ADI公司生产的16位、6通道同步采样芯片AD73360L;DSP选用TI公司生产的32位定点型TMS320VC5502。

实际电压信号U0经信号调理电路后送入ADC进行模拟信号到数字信号的转换，再通过ADC的串行外设接口(serial peripheral interface，SPI)将采样所得的数字信号送入DSP进行处理，最后在DSP中完成本文所提基于分段加Nuttall窗插值FFT的电压暂降检测方法，即可得到电压暂降信号的3个重要特征量。

图5 测试平台结构框图

在实际测试中，采用Fluke 6105A作为信号标准源生成电压暂降信号，设置如下参数：U0=220 V；暂降深度为0.8；基波频率为50 Hz，并随机加入3、5、7次谐波；ADC采样率为6.4 kHz，采样长度为10个周波；暂降发生和结束的时刻分别为0.08 s和0.12 s。实际检测所得信号的起始时刻为0.079 7 s，结束时刻为0.119 8 s，暂降深度的相对误差0.01%。由实际测试数据可知，基于分段加Nuttall窗插值FFT的电压暂降检测方法所得测试结果完全满足国家标准GB/T 30137—2013《电能质量 电压暂降与短时中断》的检测误差要求[16]。

4 结论

本文提出了一种基于分段加Nuttall窗插值FFT的电压暂降检测方法。该方法具有计算简单、鲁棒性好等特点，能够准确、有效地检测电压暂降信号的3个重要特征量(暂降幅值、持续时间和相位跳变)。与现有检测方法相比，本文方法具有检测精度高、抗噪性好、易于嵌入式实现等优点。仿真试验和实际构建的ADC+DSP硬件测试平台验证了本文方法的准确性和可靠性。所提方法对于暂降敏感设备特征分析、类型划分以及暂降监测、评估和治理具有重要意义。