潜变量增长混合模型在学龄儿童体质指数变化轨迹分析中的应用

大连医科大学公共卫生学院卫生统计教研室(116044) 雷 芳 宋桂荣 刘启贵 胡冬梅 李国荣 唐 晓

【提 要】 目的 探讨潜变量增长混合模型(latent growth mixture modeling，GMM)和潜类增长模型(latent class growth model，LCGM)在识别儿童体重增长变化潜在类别上的应用。方法 以大连市932名6～12岁学龄儿童的体检纵向数据为例。运用Mplus8.3软件构建不同性别儿童体质指数(body mass index，BMI)变化的GMM和LCGM模型。结果 LCGM模型对男女学龄儿童的生长轨迹均识别出3个增长趋势不同的亚组：“稳定组”、“肥胖组”、“偏瘦组”；GMM模型对男性学龄儿童的生长轨迹识别出2个增长趋势不同的亚组：“稳定增长组”和“肥胖增长组”。结论 GMM和LCGM模型可以识别学龄儿童BMI发展轨迹的异质性，拓展了描述儿童体重动态变化的方法研究。

儿童生长发育状况关系到社会发展水平及健康水平。体质指数(body mass index，BMI)，是国际上常用于评价儿童生长发育、营养状况及胖瘦程度的重要指标[1]。在对BMI多次监测构成的纵向数据的研究中，广义线性混合模型、多元线性回归模型等模型是目前常见的分析方法，但这些研究方法都只对调查对象进行了一个群体性BMI轨迹研究，并未对群体内部BMI发展异质性进一步研究与探索。然而，在实际情况中，不同个体BMI变化的轨迹可能是存在差异的，比如，某一儿童群体的BMI随时间变化可能会呈现“持续保持平稳”、“明显升高”、“明显降低”等不同类别的变化轨迹，即研究群体内部可能存在BMI发展趋势不同的亚群。潜变量增长混合模型(latent growth mixture modeling，GMM)和潜类增长模型(latent class growth model，LCGM)是目前较先进的纵向数据建模方法，可用于识别随时间变化有不同发展趋势的群体，探究并确定研究群体中各个亚群的发展趋势及轨迹特征。本研究通过对大连市学龄儿童纵向数据的分析，来阐述这两个模型在BMI发展轨迹中的应用。

资料与方法

1.模型原理

传统的潜变量增长曲线模型(latent growth curve model，LGCM)可采用线性、二次、更高次曲线或分段函数来模拟纵向数据的轨迹，以线性函数为例：

yit=αi+βit+εit

αi=α0+μαi

βi=β0+μβi

其中，yit表示个体i在t时点(年龄)的应变量值，t为测量时点，αi为个体i的截距，即个体指标的初始水平，βi为个体i的斜率，即个体i指标的发展速度。α0和β0分别为群体的平均截距和平均斜率，也称为固定效应，μαi、μβi分别为个体i的截距和斜率的变异程度，也称为随机效应，εit为随机误差。此线性模型的潜变量为截距潜变量和斜率潜变量。

GMM模型在LGCM的基础上增加了分类潜变量，可以将存在异质性的群体分成若干个亚群，描述各个亚群的发展轨迹及其内个体的发展变化的差异，该模型存在两种潜变量：(1)连续潜变量，包含增长特征参数，即随机截距、随机斜率或随机加速度等因子。(2)分类潜变量：将研究群体分成互斥的亚群来描述群体的异质性[2]。

GMM模型的表达公式如下(以线性函数为例)：

yit=P(C=k)·(αik+βikt+εitk)

αik=α0k+μαik

βik=β0k+μβik

分类潜变量C表示群体可分成的若干个亚群，共包含k个类别；P(C=k)表示个体i属于第k类的概率；αik和βik分别表示个体i在第k类的截距和斜率，α0k表示第k类的截距均值，用于描述第k类的平均初始值，μαik表示第k类个体间初始值的差异；βik表示第k类的斜率总均值，描述该类的总平均变化率，μβik表示第k类个体间平均变化率的差异。εitk表示个体i在第k类的残差[3]。

LCGM模型是GMM模型的特例，与GMM模型使用随机系数来估计个体的斜率和截距不同，LCGM模型假设在同一亚组内个体的斜率和截距均相同，类别组内的发展轨迹不存在个体差异[4]。

LCGM模型的表达公式如下(以线性函数为例)：

yit=P(C=k)·(αik+βikt+εitk)

αik=α0k

βik=β0k

模型拟合优劣的评价指标：(1)模型拟合评价指标有AIC 、BIC、aBIC、Entropy，前三个指标越小说明模型拟合情况越好，Karen等人研究表明，aBIC是最好的信息指标[5]。Entropy评价模型分类的精确性，取值在0～1，一般大于0.8认为该模型的分类精确性较高[6]。(2)模型亚组分类比较包括VLRT和BLRT检验，当比较含k类的模型与k-1类模型拟合情况时，若检验结果P<0.05，则表示含k个亚类的模型更好，反之，则k-1类模型拟合较好。

2.资料来源

资料来源于2003年至2009年大连市四个区小学的队列研究数据，数据收集情况见文献[7]。共有515名男童和417名女童共932名学生纳入 6年的队列研究，资料包含研究对象1到6年级每年的身高(cm)和体重(kg)，BMI=体重/身高2(kg/m2)。按照WHO 2007分性别和年龄别的标准分别计算男童及女童BMI的标准化评分BMI-Z。本研究经大连医科大学公共卫生学院与伦理委员会批准，所有参与者、家长或法定监护人均已知情同意。

3.模型方法

由于男童和女童的体质存在差异性，且体脂发育不同步，故按性别不同分别进行建模分析[8]。本研究分两部分进行：将6年监测的BMI-Z作为观测变量分别拟合线性、二次函数的LCGM和GMM；以前一步得到的最优模型的分类和基线身高作为自变量，以6年身高的总增长值作为因变量进行多元回归分析，来探讨BMI发展趋势不同的儿童身高增长的差异。

使用Mplus 8.3软件进行LCGM和GMM模型，使用SPSS 20.0对人口学变量进行统计描述和多元回归分析。

结 果

1.研究对象基本特征

共有932名学生纳入本次研究，其中，男童515名(55.3%)，女童417名(44.7%)，基线的平均年龄为(7.10±0.34)岁；基线的平均BMI：男童(16.31±2.67)kg/m2，女童(15.50±2.16)kg/m2。

2.儿童BMI-Z的LCGM模型拟合结果

LCGM模型拟合男女童的BMI-Z值发展情况的结果见表1和表2。模型结果显示，男童和女童都是含3个潜在类别的二次函数的LCGM模型拟合情况较好。

表1 LCGM模型拟合统计量结果(男童)

表2 LCGM模型拟合统计量结果(女童)

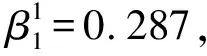
表3 学龄儿童BMI-Z发展趋势的LCGM模型参数估计结果

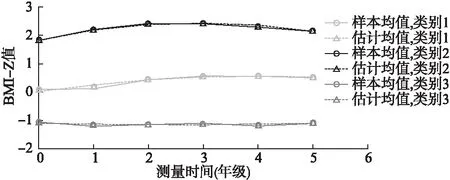
图1 男童LCGM增长趋势图(样本均值和估计均值)

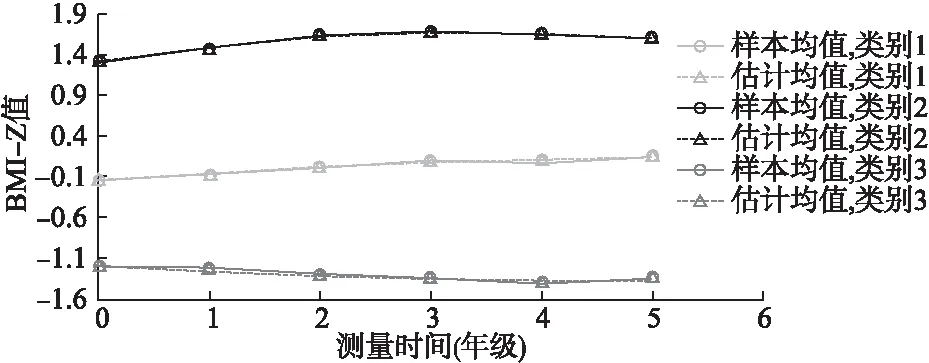
图2 女童LCGM增长趋势图(样本均值和估计均值)

3.儿童身高变化影响因素的多元回归分析

多元回归模型的因变量为6年身高增长值，自变量为基线身高和LCGM确定的亚组分类，其中，将“稳定组”设置为对照组。结果显示男女童中肥胖组与稳定组对比，身高变化差异均无统计学意义(P>0.05)；而男女童偏瘦组均比稳定组平均身高降低。两组结果提示，体重增加并不能使得身高增加，而偏瘦会使身高增加不足。结果见表4。

表4 学龄儿童身高增长影响因素的logistic回归结果

4.儿童BMI-Z的GMM模型拟合结果

运用GMM模型对儿童的BMI-Z值增长情况进行群体异质性分析的过程和LCGM类似。比较不同曲线及不同类别模型的相关拟合评价指标，男童含2个潜在类别二次增长的GMM模型拟合较好，模型参数估计结果见表5，增长趋势图见图3。在第一类别中，男生BMI-Z变化的特点是初始值略低于标准值，随时间变化较缓慢增长，但增长速度减慢，命名为“稳定增长组”；截距、斜率、二次项系数的方差均有统计学意义，说明这一亚组个体间的BMI-Z初始值、增长率和增长加速度均存在差异；这一类别中增长特征参数间的协方差有统计学差异，表明，男生BMI-Z初始值与斜率、增长加速度有关联，BMI-Z初始值越高，增长速度越快，增长加速度会减缓。在第二类别中，男生初始值高于标准值，且随年龄增长而增长，增长速度减缓，命名为“肥胖增长组”；男生这一亚组中截距、斜率、二次项系数的方差分别为2.238(P<0.05)、0.167(P<0.05)、0.001(P=0.101)，说明该类别的男生BMI-Z初始值和增长率存在个体差异，而增长速度没有个体差异；该组协方差结果表明，男生BMI-Z初始值与增长斜率、增长加速度均有关联，BMI-Z初始值越高，增长速度越慢，但增长加速度增大。

表5 男童体重发展趋势的GMM模型参数估计结果

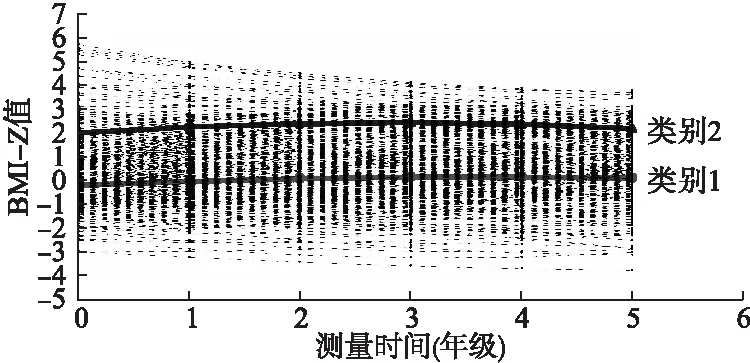
图3 男童GMM增长趋势图(样本均值和估计均值)

GMM模型在本例女童中应用的效果不佳，根据模型拟合评价指标提示，女童含2个潜在类别二次增长的GMM模型拟合较好。但从表6中可以看出，第一亚组中人数占比为98%，第二亚组人数占比只为2%，研究者普遍认为分类结果中每组人数至少要大于等于5%样本量[9]。亚组中样本数量过少，模型分类结果的可靠性低。女童BMI-Z的增长趋势图见图4。

表6 女童体重发展趋势的GMM模型参数估计结果

图4 女童GMM增长趋势图(样本均值和估计均值)

讨 论

以往许多关于学龄儿童BMI的研究重点关注的是儿童肥胖率与超重率[10-11]，但探索儿童随着年龄增长BMI的发展轨迹可以揭示体重的动态变化。学龄儿童在生长发育期间，存在着不同体重变化轨迹的亚群体[12]。本文基于LCGM和GMM两个模型探索了学龄儿童BMI的变化轨迹，研究发现学龄男女生均存在不同类型的变化轨迹，且回归模型提示“肥胖组”身高增长并不显著，说明超重肥胖并不能对身高有所贡献。故应积极对此类人群体脂进行干预与控制，促进儿童体质健康发展。

关于学龄儿童BMI的队列研究中，常用的研究方法为传统的线性混合模型，这样的方法假定所有人群来自同一体，即群体内每个个体的生长轨迹具有相同的截距和斜率等增长参数，显然这种方法对异质性较强的儿童群体有很大的局限性。将潜在类别引入增长模型中，既可以刻画学龄儿童的BMI增长趋势又可以探讨是否存在不同的潜在亚组。GMM模型允许亚组内存在个体差异，而LCGM模型中假设各个亚群的发展轨迹不存在个体差异。两种模型的最大优点在于，将连续潜变量和分类潜变量结合起来，通过分类潜变量将研究总体分为不同的亚群，根据连续潜变量来描述不同亚群的增长趋势，甚至可以识别亚群内个体间是否存在差异[3]。因此GMM和LCGM是分析纵向数据的两种较先进的方法。

由于GMM模型允许潜变量方差与协方差的估计，故对有些数据模拟效果不佳。在本研究中运用GMM模型对女童BMI-Z进行群体异质性分析时，分类结果出现某类别样本数量过少的情况，模型分类结果的可靠性低。该模型分类精确性的主要影响因素为潜类别间距离和类别内方差，若潜类别间距离越小，模型分类效果越差；若类别内方差越大，类别之间重叠的部分越大，则将个体划分到特定类别组就越困难[13-14]。因此GMM和LCGM模型的选择性与适用性也是未来研究中需要不断总结的问题。