基于有向无环图和线性回归理论定量分析常见混杂的影响*
荆 典 段重阳 谭 铭,2△ 陈平雁△
【提 要】 目的 结合有向无环图(directed acyclic graphs,DAGs)与线性回归模型,提出常见混杂的定量分析方法。方法 针对典型的两种DAGs(情形1:X←C→Y;情形2:X←C1→M←C2→Y),基于线性回归理论给出偏倚大小的定量表达式,并探讨各参数对因果效应估计的影响。结果 对于情形1的DAG,暴露X与结局Y的因果效应估计需通过关闭二者间后门路来控制混杂C,否则X与Y间因果估计会受到混杂偏倚的影响。理论推导结果显示,若只改变C对X的效应则同时会增加X的方差,此效应的强弱对混杂偏倚的影响是非单调的,除非在改变C与X的效应的同时控制X的方差不变,而C与Y间的效应强弱对混杂偏倚的影响则是单调的。对于情形2,又称M-DAGs无需做变量控制即可做X与Y的因果估计,但当错误地控制碰撞点M后会导致后门路径打开而出现混杂,此时需进一步控制C1和(或)C2来关闭后门路径。我们用回归理论解释了该结果,并且得到当C1与X相关性较高时,同时控制C1和M的方法结果会不稳定。结论 本研究基于有向无环图,根据线性回归理论推导出常见混杂的定量分析方法,该方法也适用于无法观测的混杂,为多因素因果推断提供了一种实用工具。
在多变量的因果推断中,如何选择纳入回归分析的协变量始终是一个研究的热点问题[1-4]。有向无环图(directed acyclic graphs,DAGs)应用甚广,能够基于预先假定的因果关系找到应校正的混杂因素集合[5-8]。然而,DAGs只能定性表达混杂的影响[9-11]。如何结合DAGs的定性方式,又能定量表达混杂的影响是一个值得研究的课题。因此,本研究将通过DAGs说明传统的混杂偏倚和由于校正碰撞点所引起的选择偏倚,并经由线性回归理论推导讨论校正偏倚及改变变量间关系对于偏倚大小的影响,以期对DAGs的结论用回归理论做解释说明,并同时给出DAGs无法给出的混杂定量影响的相关结论。
方 法
DAGs利用图示方法描述待研究的处理或暴露(X)、结局(Y)以及协变量之间的因果关系[10,12]。“后门路径(backdoor path)”是DAGs的一个重要概念,其定义为即使移除所有从暴露指向其子代变量的路径,在暴露和结局间仍存在一条非因果效应的路径[12-13]。如果X和Y之间除因果路径还存在开放的后门路径,在估计X和Y之间的因果效应时就会产生偏倚。由X和Y的共同原因导致开放的后门路径所引起的偏倚称为混杂偏倚(confounding bias),而由两个变量(其中之一为X或/与X相关的变量,另一为Y或/与Y相关的变量)的共同效应导致开放的后门路径所引起的偏倚称为选择偏倚(selection bias)或碰撞点偏倚(collider bias)。需要注意的是,对于碰撞点施加干预会打开额外的后门路径并引起偏倚,如碰撞点DAG(M-DAG)[8,12-14]。
图1为探讨混杂常用的DAGs,其中图(a)、(b)、(c)表示暴露X与结局Y之间除了因果路径X→Y外,还存在开放的后门路径,即(a):X←C→Y;(b):X←C←U→Y;(c):X←U→C→Y,因此X与Y之间存在混杂。若要控制混杂则需要关闭后门路径,如采用协变量校正、分层、匹配等方法。图(d)、(e)常用于说明并非所有变量都可以校正,有时校正变量反而会引起混杂。由于碰撞点的存在,如(d):C1→M←C2;(e):X→C←U,除了因果路径X→Y外,并没有开放的后门路径,因此不存在混杂。但是,如果过度校正了碰撞点,则反而打开了后门路径,引起选择偏倚。上述5个DAGs中我们可以发现(b)和(c)为(a)的变形,(e)为(d)的变形,所以我们选择具代表性的DAG(a)和DAG(d),结合线性回归模型建立控制混杂的定量分析方法[12,15-16]。

图1 常见混杂的DAGs
1.DAG(a)
DAG(a)为最常见的一种混杂偏倚,即由于共同原因C的存在导致X和Y之间存在开放的后门路径(X←C→Y)。例如,在研究体重(X)是否会影响收缩压(Y)时,发现年龄(C)均会对二者造成影响,即使体重和收缩压不存在真实的因果效应,仍能通过年龄(C)发现关联[12]。如下我们用回归理论解释该关系。
表示X受C的影响,令X=γ0+γ1C+εx;表示Y受X和C的共同影响,令Y=λ0+λ1C+λ2X+εy,其中γ1、λ1和λ2分别为C对X、C对Y和X对Y的效应;εx和εy分别为X和Y的噪声。
由线性回归模型Y=α+βX+ε拟合X和Y的效应,可得到β的估计值如下:
(1)
其中,Cov(X,Y)是X和Y的协方差,Var(X)是X的方差,SD(X)和SD(Y)是X和Y的标准差,rxy是X和Y的相关系数,并且rxy=Cov(X,Y)/[SD(Y)SD(X)]。由上述方程可进一步得到C同X和Y的相关关系如下:
Cov(C,X)=γ1Var(C)
Cov(C,Y)=λ1Var(C)+λ2Cov(C,X)=
(λ1+λ2γ1)Var(C)
Cov(X,Y)=λ1Cov(C,X)+λ2Var(X)=
2λ1λ2Cov(C,X)+Var(εy)=
(2)
由式(1)和式(2)可得β的期望为:
(3)
rxy的期望为:
(4)
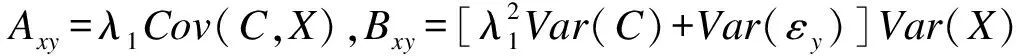
(5)
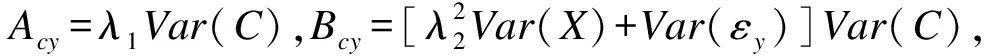
(6)
更特殊的,当X对Y的效应为0时,即λ2=0时,式(2)可简化为:
Cov(C,X)=γ1Var(C)
Cov(C,Y)=λ1Var(C)
Cov(X,Y)=λ1γ1Var(C)
(7)
以及
(8)
2.DAG(d)
DAG(d)被称之为M-DAG,其中存在一个同时受到暴露X和结局Y的父代(ancestor)C1和C2影响的碰撞点M,此时校正M将会打开原本闭合的后门路径(X←C1→M←C2→Y)。例如,研究总胆固醇(X)对收缩压(Y)的影响时,发现年龄(C1)会影响总胆固醇(X),也可影响空腹血糖(M)。与此同时,心率(C2)也会影响收缩压(Y)和空腹血糖(M)。当研究对空腹血糖进行校正时,就会打开原本闭合的后门路径从而引起偏倚[12]。如下我们同样用回归理论解释该关系。
令M=α0+α1C1+α2C2+εm,X=γ0+γ1C1+εx,Y=λ0+λ1C2+λ2X+εy,其中α1、α2、γ1、λ1、λ2分别为C1对M、C2对M、C1对X、C2对Y、X对Y的效应。εm、εx和εy分别为M、X和Y的噪声。由线性回归模型Y=β0+β1X+ε拟合未校正M时X和Y的效应,用模型Y=β0+β1X+β2M+ε拟合校正M的情况,以及用模型Y=β0+β1X+β2M+β3C+ε(C为C1或C2)拟合同时校正M和C1或C2时的情况。基于回归理论可知估计值β为:
(9)
由公式(9)可得由模型Y=β0+β1X+β2M+ε得出校正M后β1的估计值:
(10)
对于同时校正M和C1或C2,可得:
(11)
式中C表示C1或C2。
令H=XTX,可得β1的估计值为:
(12)
及:
(13)
更特殊的,当X对Y的效应为0时,即λ2=0有:
Cov(C1,X)=γ1Var(C1)
Cov(C1,M)=α1Var(C1)
Cov(C1,Y)=0
Cov(C2,X)=0
Cov(C2,M)=α2Var(C2)
Cov(C2,Y)=λ1Var(C2)
Cov(X,Y)=0
Cov(X,M)=α1γ1Var(C1)
Cov(M,Y)=α2λ1Var(C2)

(14)
若校正C1,可知Cov(X,Y)=0且Cov(C1,Y)=0,则公式(13)可简化为:
(15)
若校正C2,可知Cov(X,Y)=0且Cov(C2,X)=0,则公式(13)可简化为:
(16)
结 果
基于前面理论推导结果,我们可讨论各参数对偏倚大小的影响。为形象展示各参数间关系,在具体讨论中我们同时基于一假定的参数绘制了关系曲线,结果见图2。
1.DAG(a)
(1)不对C校正时X与Y效应估计偏倚大小
由公式(3)可知,不对混杂因素C进行校正将会恒定错误估计真实因果效应为
(17)
具体可见图2(A)。
针对之前提到的实例,当研究体重(X)对收缩压(Y)的因果效应时,若不校正年龄(C)这一混杂因素,则会错误估计真实因果效应。并且当体重(X)确定后,其方差Var(X)相对确定,此时偏倚大小与年龄(C)的方差Var(C)、年龄(C)对体重(X)的因果效应γ1,年龄(C)对收缩压(Y)的因果效应λ1在其余二者固定不变的情况下成线性正相关关系。
进一步研究改变C对X和C对Y的相关关系所带来的可能影响。本研究考虑两种方式改变其相关,其一是直接增加C对X或C对Y的因果效应,如增大年龄(C)对体重(X)的影响或是其对收缩压(Y)的影响;其二是通过对X或者Y施加噪声(给定SDs)。
(2)C对X和C对Y效应大小对X与Y效应估计偏倚大小的影响
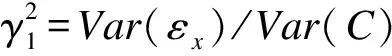
当仅增加C对Y效应λ1时,Cov(C,Y)、Cov(X,Y)、Var(Y)、E(rxy)和E(rcy)随之增加,从公式(17)知,此时除了λ1变化其余各项均不变,因此偏倚(17)随之线性增加。具体可见图2(C)。
(3)X、Y噪声大小对X与Y效应估计偏倚大小的影响
以特殊情形,即不考虑X和Y存在因果效应为例,如假设体重(X)不会影响收缩压(Y),则可由公式(7)、(17)知,当仅增加X噪声标准差SD(εx)时,Var(εx)和Var(X)随之增加,故偏倚(17)随之下降。当仅增加Y噪声标准差SD(εy)时,偏倚(17)不变。当X和Y因果效应不为零时,即假设体重(X)会影响收缩压(Y)时,则基于公式(2)上述结论依然成立。具体可见图2(D)、(E)。
(4)对变量间相关系数估计的影响
对于DAG(a),首先探讨暴露X对结局Y真实因果效应改变所带来的可能影响。由公式(2)~(5)可知固定其他变量不变时,增大X对Y的因果效应λ2,如体重(X)对收缩压(Y)影响λ2增大时,Var(X)、Var(C)、Var(εy)、Cov(C,X)和λ1不变,Cov(C,Y)、Cov(X,Y)和Var(Y)逐渐增加。年龄(C)和体重(X)的相关系数rcx的期望不随λ2的增加而改变,而体重(X)和收缩压(Y)相关系数rxy的期望及年龄(C)和收缩压(Y)相关系数rcy的期望随λ2的增加而增大。
当X和Y的因果效应为0时,如假设体重(X)不会影响收缩压(Y),当仅增加体重(X)噪声标准差SD(εx)时,可由公式(7)、(8)知E(rxy)、E(rcx)会随着SD(εx)的增加而降低,而E(rcy)不变。当仅增加收缩压(Y)噪声标准差SD(εy)时,Var(εy)和Var(Y)增加,故仅E(rxy)和E(rcy)随着SD(εy)的增加而降低。当X和Y的因果效应不为0时,即体重(X)会影响收缩压(Y),仅增加体重(X)噪声标准差SD(εx)时Var(Y)也会增加,此时E(rxy)随之不再单调下降,E(rcy)随之下降,其余结论同上述保持一致。具体可见图2(A)~(E)。

表1 DAG(a)结果汇总
2.DAG(d)
对于DAG(d),主要研究混杂因素的校正对X和Y因果效应估计的影响。此时若不考虑X和Y存在因果效应,则由公式(3)可知通过模型Y=β0+β1X+ε所得的β1估计值是无偏的,即不对任何变量进行校正时不存在偏倚。由公式(10)可知对M进行校正时,Cov(X,M)和Cov(M,Y)会导致偏倚,且偏倚的期望为
(18)
上述关系示例图见图2(F)。

图2 改变各参数对变量间关系的影响
例如研究总胆固醇(X)对收缩压(Y)的影响时纳入空腹血糖(M)会存在偏倚。当总胆固醇(X)对收缩压(Y)不存在影响时,由公式(15)可知纳入所在年龄(C1)后,X和C1以及M和C1的协方差会抵消X和M的协方差,即同时校正M和C1所得的估计值无偏;由公式(16)可知纳入心率(C2)后,Y和C2以及M和C2的协方差会抵消Y和M的协方差,即同时校正M和C2所得的估计值无偏。当X对Y的效应不为0时,即总胆固醇(X)对收缩压(Y)存在影响时,由公式(13)知该结论同样成立,即在存在选择偏倚时要想得到无偏的效应估计可将所在年龄(C1)或心率(C2)纳入模型分析。
由于X和C2的相关系数恒定为0,而X和C1的高度相关使公式(15)中H的行列式接近于0,同时校正M和C1相比于校正M和C2会更加不稳定。
实例分析
由于实际应用中我们无法获得真实的效应,因此无法对偏倚进行准确评价,本实例分析我们基于真实数据背景产生模拟数据,对本文中理论推导结果进行验证。模拟数据的参数设置基于东莞寮步社区高血压人群调查体检数据库得到的汇总数据。针对DAG(a)和DAG(d)模拟研究体重(X)或总胆固醇(X)对血压收缩压(Y)的影响[17-18]。本研究不关注抽样误差影响因此设置较大样本量,基于检验效能大于95%设置样本量为800。
对于DAG(a),年龄(C)服从N(60,13.7)的正态分布,体重(X)(N(64.5,12.2))和收缩压(Y)(N(136.1,16.3))的噪声均服从N(0,1)的正态分布,并分别由回归方程X=86.4-0.36C+εx和Y=117+0.22C+0.1X+εy产生。
对于DAG(d),年龄(C1)服从N(60,13.7)的正态分布,心率(C2)服从N(72,11)的正态分布,总胆固醇(X)(N(199.5,45.0))、空腹血糖(M)(N(5.35,1.65))和收缩压(Y)(N(136.1,16.3))的噪声均服从N(0,0.1)的正态分布,并分别由回归方程X=187+0.22C1+εx、Y=126+0.083C2+0.03X+εy和M=4.1+0.013C1+0.03C2+εm产生。
由表2可知,DAG(a)中校正混杂因素年龄(C)后得到的体重(X)系数估计值结果无偏,而不校正则会低估0.587个单位(公式(17)计算结果为0.591)。而DAG(d)中,仅纳入总胆固醇(X)以及同时校正空腹血糖(M)和年龄(C1)或心率(C2)所得的系数估计值均无偏,但同时校正C1所得的结果不稳定。若直接纳入总胆固醇(X)和空腹血糖(M)则会低估0.151个单位(公式(18)计算结果为0.140)。实例分析情况均同本研究理论推导结果一致。

表2 回归分析结果
讨论与结论
本研究基于两种常见的DAGs,通过线性回归理论对混杂偏倚和因选择偏倚导致的混杂进行了分析,结果与DAGs的图示规则保持一致。此外,本研究给出了偏倚大小的定量表达式(见公式(17),(18)),探讨了不同方式改变混杂因素同处理或结局的效应时对偏倚大小的影响。
对于经典的混杂DAG,当我们考虑混杂与暴露的效应对偏倚影响的大小时,需同时考虑暴露的方差的控制,使其更符合研究者的设定。比如现实数据分析中,若要考虑未观测的混杂导致的偏倚影响大小时,对于观测到的暴露,我们应该假设其方差固定,然后改变假定的混杂与暴露的效应,以评价其可能的影响。如基于数据分析得出X与Y的回归系数为2,此时可以讨论若真实回归系数为0时,存在影响多大的潜在混杂C,可使得估计出的回归系数为2,即当存在影响多大的潜在混杂C时可扭转当前回归系数2到0或者负值。基于公式(17),此时X的方差已知,则假定真实的回归系数为0时,λ1γ1Var(C)作为一个整体取值为λ1γ1Var(C)=2Var(X)可使得估计出的有偏的回归系数为2,此时可将该值与观测到的专业上具有意义的各混杂λ1γ1Var(C)相应值进行比较,来判断该λ1γ1Var(C)=2Var(X)存在的可能性,如果该可能性较小,则认为当前估计结果受潜在混杂影响而扭转结局的可能性较小[19]。
对于M-DAG,不对任何协变量做处理时估计值无偏。若对碰撞点进行校正,还需校正位于碰撞点和处理或结局间的变量以得到真实因果效应的无偏估计。在变量间相关性较强的情况下同时校正碰撞点和位于碰撞点和结局间的变量所得的估计结果会更稳定。
由于篇幅限制,本研究仅考虑变量服从正态分布的情况。虽然结局指标的类型不会影响DAGs的混杂理论,但在考虑实际应用的回归分析策略时,结局的类型不能忽略,例如二分类结局利用logistic回归对协变量进行校正可能同标准线性回归大不相同。同时,变量间成非线性关系时混杂因素的影响也有待探讨。
本研究建立了将DAGs与线性回归模型结合估计混杂偏倚的定量分析方法,该方法还适用于无法观测的混杂,为多因素因果推断提供了一种实用工具。

