基于改进MCCIPM的含TCPST电力系统最优潮流计算

张宁宇，张恪，李群，刘建坤，赵静波，孙国强

(1.国网江苏省电力有限公司电力科学研究院，江苏 南京 211103；2.河海大学能源与电气学院,江苏 南京 211100)

0 引言

随着经济的快速发展，我国部分地区的电网供电能力已无法满足人们日益增长的生活需求，寻找缓解此矛盾的方法是当今电网建设的首要任务[1—5]。可控移相器(thyristor controlled phase shifting transformer，TCPST)作为新一代柔性交流输电(flexible AC transmission system，FACTS )装置，可通过调整可控元件参数实现对母线电压和线路潮流的灵活控制，并有效提高分区供电能力[6—7]，因此，TCPST具有广泛的应用前景。

系统最优潮流(optimal power flow，OPF)是电力系统优化运行领域的重要分支[8—9]，因此，研究含TCPST的电力系统OPF问题可充分发挥TCPST对线路潮流的调控能力，进而提高电网运行的安全性[10—12]。文献[13—14]将FACTS 最优参数的设定问题描述为优化问题，并通过求解OPF得到FACTS装置的可控参数值。文献[15]验证了TCPST在线路潮流灵活控制、降低系统网损方面的有效性。文献[16]对含TCPST等FACTS装置的电力系统进行最大输电能力的OPF计算，验证了TCPST提高系统运行经济的能力。文献[17]采用原对偶内点法(primal dual interior point method，PDIPM)完成含TCPST系统的OPF计算，然而在拓扑结构复杂的大系统中，PDIPM很可能出现收敛性差、甚至不收敛情况。针对内点法求解易出现方向错误、计算效率低等问题,采用高阶算法来提高牛顿方向的多中心-校正内点法(multiple centrality-correction interior point method，MCCIPM)逐渐应用于电力系统优化计算中。文献[18]基于鲁棒性好的MCCIPM完成系统OPF计算，验证了MCCIPM对求解OPF问题的有效性。文献[19]利用MCCIPM完成可用输电能力的计算，提高了优化问题计算的收敛性。

文中首先依据TCPST工作原理获得其等效功率注入模型；其次以系统有功损耗最小为目标确定计及TCPST的OPF模型；然后针对目前MCCIPM参数设置保守、迭代计算时间长等问题，提出重新配置部分映射参数、改进MCCIPM的仿射方向迭代步长；最后，采用改进MCCIPM对IEEE 14、IEEE 30和IEEE 118节点系统算例展开测试。算例结果表明，文中方法收敛性好、计算效率高，可充分发挥TCPST的潮流控制能力，提高系统经济性。

1 TCPST原理及潮流计算模型

1.1 TCPST原理及结构

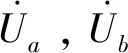
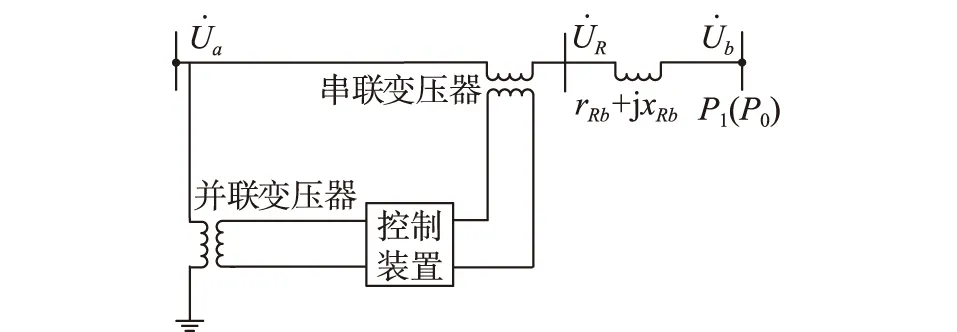
图1 TCPST结构模型Fig.1 Structure model of TCPST

P0=(UaUb/XL)sin(φb-φa)

(1)

P1=(URUb/XL)sin(φb-φR)

(2)

式中：XL为线路电抗；φx为节点x的相角，x=a,b。对比式(1)、式(2)可知，TCPST通过串联变压器向所在线路注入电压从而改变线路末端电压幅值和相角、控制线路的潮流分布，最终达到提高系统可靠性的目的。

1.2 TCPST潮流计算模型

图2 含TCPST的网络示意Fig.2 Schematic diagram of network with TCPST

根据电路原理，TCPST等效电压源和电流源可分别表示为：

(3)

(4)

式中：φ为TCPST的移相角。同时：

(5)

(6)

基于以上变换，可将TCPST移出网络，将TCPST的作用等效为两端的节点注入功率，其节点注入功率模型如图3所示。PTa，PTb，QTa，QTb分别为TCPST对节点a和b的等效注入有功功率和无功功率。

图3 TCPST等效功率注入模型Fig.3 Equivalent power injection model of TCPST

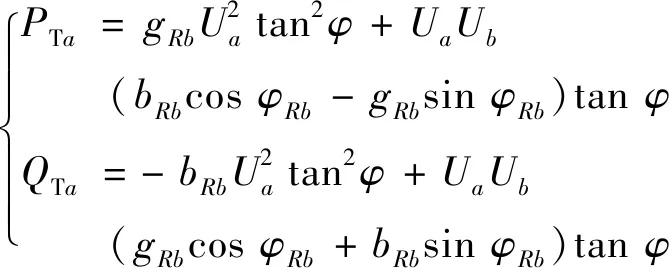
(7)

(8)

式中：gRb，bRb分别为TCPST所在支路的等效电导和电纳，且gRb+jbRb=(rRb+jxRb)-1；φRb为线路Rb的相角。当TCPST加入系统之后，可用上述等效注入功率来表示TCPST对系统潮流带来的影响。考虑到在高压输电线路中，线路的等值电导远小于线路的等值电纳，因此可以忽略线路的等值电导。由于TCPST相角和节点电压相角差不大，所以可以忽略附加节点注入功率的无功分量而只计有功分量。因此，等效功率注入可简化为：

(9)

(10)

2 计及TCPST的电力系统OPF模型

OPF问题标准形式可表示如下：

(11)

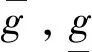
2.1 目标函数

为研究TCPST对线路有功损耗的调节作用，同时简化计算，文中以系统有功网损最小为目标函数建立基于直角坐标系的OPF模型。其目标函数如下：

(12)

式中：n为节点数；Ui，Uj分别为节点i，j的电压；Gij为导纳矩阵中对应元素的实部；θij为节点i和节点j的电压相角差。

2.2 约束条件

(1)等式约束：

(13)

式中：PGi，QGi分别为节点i上发电机发出的有功功率和无功功率，但当节点i不与发电机相连时，二者均取0；PDi，QDi为节点i的有功负荷和无功负荷；Bij为导纳矩阵中对应元素的虚部。

对于加入TCPST的线路，需在线路两端节点附加式(9)、式(10)表示的等效注入功率。因此，线路ij安装TCPST时，功率平衡方程为：

(14)

式中：PTi，PTj分别为TCPST对i和j的等效注入有功功率。

(2)TCPST容量不等式约束：

(15)

式中：*表示共轭；Smax为容量上限。

(3)TCPST调整控制不等式约束：

(16)

式中：UBmax，θBmax分别为串联侧电压源电压和相角的上限；UBmin，θBmin分别为串联侧电压源电压和相角的下限。

(4)其余不等式约束：

(17)

式中：Uimax，Uimin，θimax，θimin分别为节点i的电压幅值和相角的上、下限值；Pij,max，Pij,min，Qij,max，Qij,min分别为线路ij有功功率和无功功率上、下限；PGi,max，PGi,min，QGi,max，QGi,min分别为节点i上发电机出力的上、下限。

3 改进MCCIPM

为改善内点法在电力系统OPF计算中计算效率低等不足，当前多考虑在泰勒展开和迭代中保留部分高阶信息[22—23]，提高牛顿迭代方向的同时，减少计算迭代总次数。MCCIPM即为一种计及高阶项的改进内点法[24]，对于OPF问题，构造拉格朗日函数如下：

(18)

式中共有r个不等式约束。其中，y=[y1…ym]T，z=[z1…zr]T，w=[w1…wr]T分别为等式约束和不等式约束的拉格朗日乘子；l=[l1…lr]T，u=[u1…ur]T为不等式约束的松弛变量，将该问题转化为只含等式约束的优化问题；μ为障碍函数的扰动因子。在针对各变量偏导进行泰勒级数展开时保留扰动因子的高阶项，在预测阶段对应求出仿射方向及步长，校正阶段求解映射到超立体空间中的牛顿方向利用牛顿-拉夫逊法完成迭代计算[25]并完成下一步迭代。

为了更快速地寻求校正方向，减少迭代次数，首先将原MCCIPM的仿射方向步长增长为：

α′=min{max{α1,α2,α3}+δ,1}

(19)

式中：α1为仿射方向步长；α2为中心方向步长；α3为校正方向步长；δ为仿射步长增量。选取3个方向步长中最大值作为迭代计算的仿射步长，保证校正方向的快速性。基于此，对原、对偶变量更新可得：

m′=m(k)+α′Δb1

(20)

式中：m′为迭代更新后的各变量；Δb1为仿射方向；k为迭代次数；m=[xyzwlu]为计算中各变量。设向量p′,q′为：

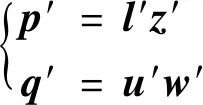
(21)

式中：l′=diag[l′1…l′r]T，z′=diag[z′1…z′r]T，u′=diag[u′1…u′r]T，w′=diag[w′1…w′r]T，且各迭代变量均通过式(19)更新获得。将p′，q′映射到超立体空间Ω=[βmaxμ1βminμ1]得到新的向量p和q。其中，μ1为预测步骤中获得的仿射扰动因子；βmax，βmin为设定的空间阈值的最大、最小值。基于以上映射，求解中心-校正方向Δb23及总牛顿方向Δb，表示为：

∇2L(m)·Δb23=n

(22)

Δb=Δb1+Δb23

(23)

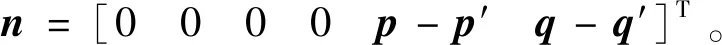
4 算例分析与测试

选取IEEE 14、IEEE 30和IEEE 118节点系统进行仿真测试，TCPST移相角的上、下限分别设置为30°和-30°。基于Matlab 2014a进行编程，测试的硬件平台基于PC机，处理器为Inter Core i5-3470 3.20 GHz CPU，8 GB内存。

根据选址原则，TCPST应安装在优化效果最好的关键支路上[27—30]，表1列出了各系统TCPST安装的最佳位置。

表1 测试系统基本参数Table 1 Basic parameters of test system

4.1 不同算法及有功网损结果

为了校验改进MCCIPM算法在求解含TCPST的OPF问题中的正确性和有效性，表2给出了PDIPM与改进MCCIPM算法求解OPF的迭代次数对比。同时，为验证TCPST具备提高系统运行经济性的能力，基于文中方法对有无TCPST系统进行OPF计算，系统有功网损对比结果如表2所示。

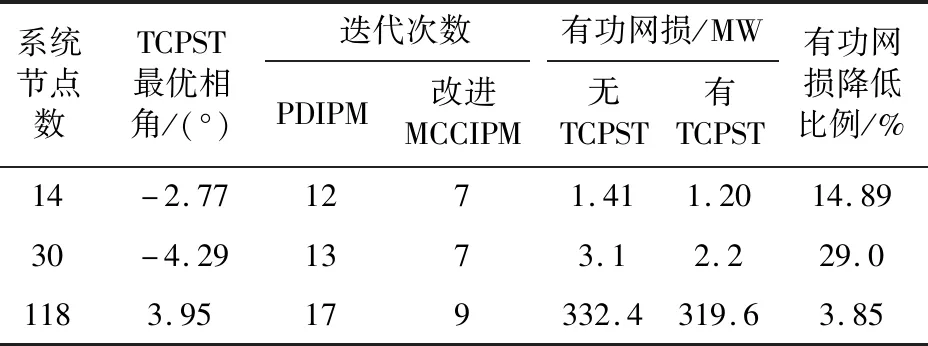
表2 OPF计算结果对比Table 2 Comparison of OPF calculation results

从2种算法的迭代次数可以看出，PDIPM对不同系统进行OPF计算时迭代次数均远高于文中所提的改进MCCIPM；且随着系统增大，PDIPM迭代次数增加明显，更易出现大系统迭代计算缓慢甚至无解等现象。反观文中算法，不同系统在OPF计算中均能快速收敛，且迭代次数受系统大小影响不大。除此之外，含TCPST系统的有功网损较原系统有明显下降，其中IEEE 14和IEEE 30节点系统有功网损降低比例较大，分别为14.29%和29.03%，调节效果明显；而IEEE 118节点系统因为系统较大，仅加入一台TCPST时，有功网损降低不明显，仅为3.85%。以上分析可知，改进MCCIPM可有效减少迭代次数，提高OPF计算效率，且在大系统OPF计算中仍具备良好的收敛性。同时，TCPST的加入可大幅降低系统运行的有功损耗，在大系统中考虑增加TCPST设备数可以更好地提高系统运行的稳定性和经济性。

4.2 电压质量结果

为了验证TCPST对系统电能质量的改善效果，对不同系统进行算例分析。图4为TCPST的加入对系统节点电压幅值的影响程度。

由图4(a)可以看出，节点8在系统未加入TCPST时有电压幅值不满足安全约束的情况，而在加入TCPST后，该节点的电压幅值满足相关要求。若以电压合格率的方式描述系统电压水平，IEEE 14节点系统在加入TCPST后，电压总合格率由初始的92.86%提高到100%。除此之外，安装TCPST之前，系统各节点的电压偏移总和为35.8%；TCPST参与调节后，电压偏移总和大幅度降低至13.5%。IEEE 30节点系统加入TCPST后，系统各节点的电压偏移总和从131.9%降低到122.1%。而在IEEE 118节点系统，仅加入1台TCPST并没有对其节点电压偏移产生明显影响。综上，在中小型系统中，TCPST的加入在降低系统有功损耗的同时，能有效减小节点电压偏差，提高系统的电能质量；且为了更好地改善大型系统电能质量，提高大系统稳定性和经济性，可酌情增加TCPST安装数量，以更好地发挥TCPST控制潮流分布、降低系统网损等功能。

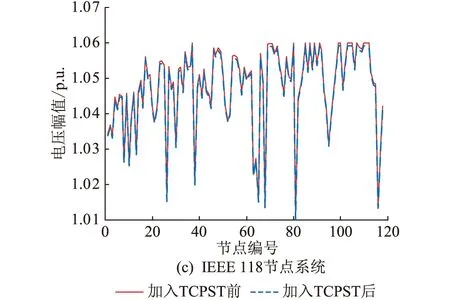
图4 TCPST加入前后各节点电压幅值对比Fig.4 Voltage amplitude comparison of each node before and after TCPST addition

5 结语

文中基于TCPST的原理及结构模型，以系统有功网损最小为目标函数，建立了计及TCPST的电力系统OPF模型，提出了基于改进MCCIPM的含TCPST系统OPF计算方法。

改进MCCIPM方法可有效提高OPF计算效率，降低迭代次数，满足系统对求解速度的要求。TCPST可降低系统运行成本，提高系统安全性，在中小型配电网络中，其调节作用更加明显。

本文得到国网江苏省电力有限公司科技项目“基于可控移相器(TCPST)的柔性交流潮流运行控制技术研究”资助，谨此致谢！