基于博弈算法的电动汽车有序充电优化及效益分析
马英姿,马兆兴
(青岛理工大学信息与控制工程学院,山东 青岛 266525)
0 引言
以化石能源为基础的能源消费结构,一定程度上造成了生态环境不可逆转的破坏[1]。为缓解能源紧张、建设美好生态环境,以电力为能源的电动汽车呈现井喷式增长[2]。然而,电动汽车的普及给电网带来了巨大的用电压力,如在充电过程中,加剧用电尖峰负荷,进一步恶化电能质量等[3—4]。
为解决这一难题,文献[5]提出根据电池寿命、电动汽车电池荷电状态(state of charge,SOC)、车主是否出行等调控次序指标,缓解电动汽车充电导致的电力不平衡,但未考虑电价对调控的影响。文献[6]提出以调峰、损失最小化和用户利润最大化为目标的电动汽车调度优化,以电动汽车为能源储备缓解负荷高峰,但未考虑用户出行计划。文献[7]考虑电动汽车车主充电首选时区,以充电时间和总系统功率损失最小化建立目标函数,缓解峰值,改善电压分布,降低功率损耗。文献[8]以传输给电动汽车最大电能为目标,提出自动开断充电模式和平滑调节充电模式,最大限度满足用户充电需求,但未考虑用户充电费用问题。文献[9]提出以功率为限制的电动汽车充电策略,可降低负荷方差,减少用户充电消费。文献[10]综合考虑电动汽车、用电器负荷、其他储能系统和可再生能源之间的能量交换,使用粒子群优化(particle swarm optimization,PSO)算法求解用电成本最小解,但忽略了用户的出行状态。
上述研究均通过某一个或几个指标有序调控电动汽车充电行为,但综合考虑充电成本与充电完成时间对电动汽车用户影响的研究较少。文中为缓解电动汽车无序充电对负荷曲线的影响,综合考虑用户充电费用和充电所需时间、售电站调峰效益和售电收益,提出用户充电时间和充电价格博弈下的电动汽车充电优化策略。售电站在分时电价基础上制定电价,减少电动汽车充电引起的峰谷差。文中利用PSO算法求解最优条件下的双方策略,以600户家庭的居民小区为例,模拟用户充电行为,对所提控制策略进行仿真验证,并对售电站的经济效益进行分析。
1 电动汽车充电行为分析
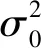
(1)
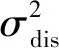
(2)
用户出行时间及行驶路程概率分布规律见图1。
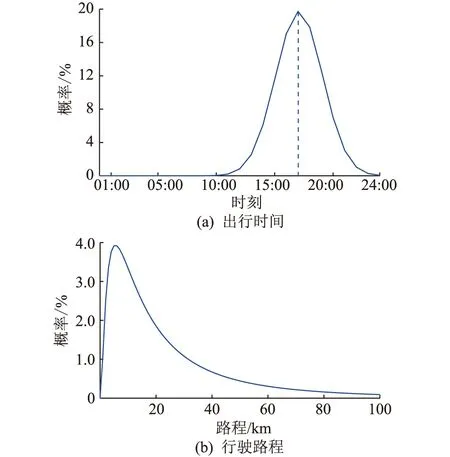
图1 用户出行时间及行驶路程概率分布Fig.1 Probability distribution of user travel time and driving distance
2 基于博弈论的电动汽车充电模型及求解
2.1 应用于电动汽车充电领域的博弈论
为了应对电动汽车即到即充的用电需求,分时电价一定程度上缓解了电力高峰时刻的用电压力,但仍无法应对电动汽车充电需求的随机性[15]。为了缓解大规模电动汽车同时充电对电网的冲击,使用斯塔克尔伯格博弈对电动汽车充电进行优化管理[16—17]。斯塔克尔伯格竞争模型是价格领导模型,决定价格的依据是:领导者决定一个价格,追随者可以看到这个价格,然后领导者根据追随者的产量决定自己的产量。二者存在先后顺序。值得注意的是,领导者在制定价格的同时,应该注意追随者的行动,追随者行为符合统计规律反应函数。简而言之,上层领导者给定初始电价,下层电动汽车使用者计算最优充电策略,实现电动汽车充电满意度最优。领导者可以预期自己决定的价格对追随者的影响。正是考虑到该因素,领导者决定的价格可以实现以追随者的反应函数为约束的营业值利润最大化。
2.2 充电模型建立
以博弈的三要素,即参与人、策略、收益建立充电模型。以售电方、电动汽车用户两方为博弈参与人,考虑二者的目标,制定博弈策略。
2.2.1 售电方目标函数
在电价博弈中,售电方是领导者,其主要职责是根据负荷曲线合理制定电动汽车充电价格,限制电动汽车聚集充电,保证负荷曲线不超过本区域功率限制。售电方通过制定充电价格获取电动汽车充电利润并调节电网压力,电动汽车充电带来的利润f1,1为:
(3)
式中:N,T分别为充电的电动汽车总数和充电的时段数;Pcharge,n为售电方电动汽车n的充电收益;Pprice,t,n,Pstart,t,n分别为博弈后的t时段电动汽车n充电电价和电网制定的分时电价;Estage,t,n为t时段电动汽车n的充电电量;t0为起始时段。
系统负荷曲线由居民区常规负荷曲线和电动汽车充电负荷曲线组成,小区引入电动汽车后的负荷为:
P∂,t=Pcommand,t+PEV,t
(4)
式中:Pcommand,t为居民小区未考虑电动汽车时的t时段基础负荷;PEV,t为t时段电动汽车充电负荷,由在该时段内充电的M辆电动汽车的充电功率PEV,t,n组成,如式(5)所示。
(5)
由于方差可以度量数据与数据均值之间的偏离程度,选取方差作为考察售电站对负荷曲线“纠偏”的贡献程度,由式(6)计算电网奖励售电方缓解电网压力做出的贡献,即调峰收益f1,2。
(6)
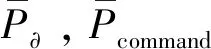
综上,售电方的收益函数F1为:
F1=f1,1+f1,2
(7)
2.2.2 售电方约束条件
充电费用会影响电动汽车普通用户的充电能力。一般来说,为保证电动汽车用户可更加灵活地选择充电时间,需对各个时段的最高充电电价进行限制。同时,设定一个最低值保证售电站的总体收益。
Pmin,t≤Pprice,t≤Pmax,t
(8)
式中:Pprice,t为售电方t时段制定的充电电价;Pmax,t,Pmin,t分别为售电方t时段可定制的最高、最低电价。
一般而言,居住小区建设时根据用户住宅面积统一规划,有一定的变压器容量。为了保证电网平稳运行,居民日常负荷应始终保持在变压器的容量Plimit之下。
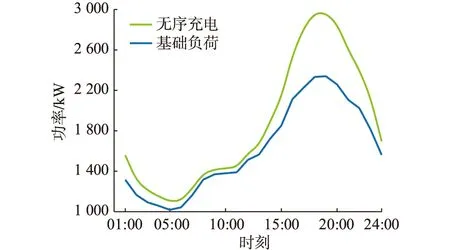
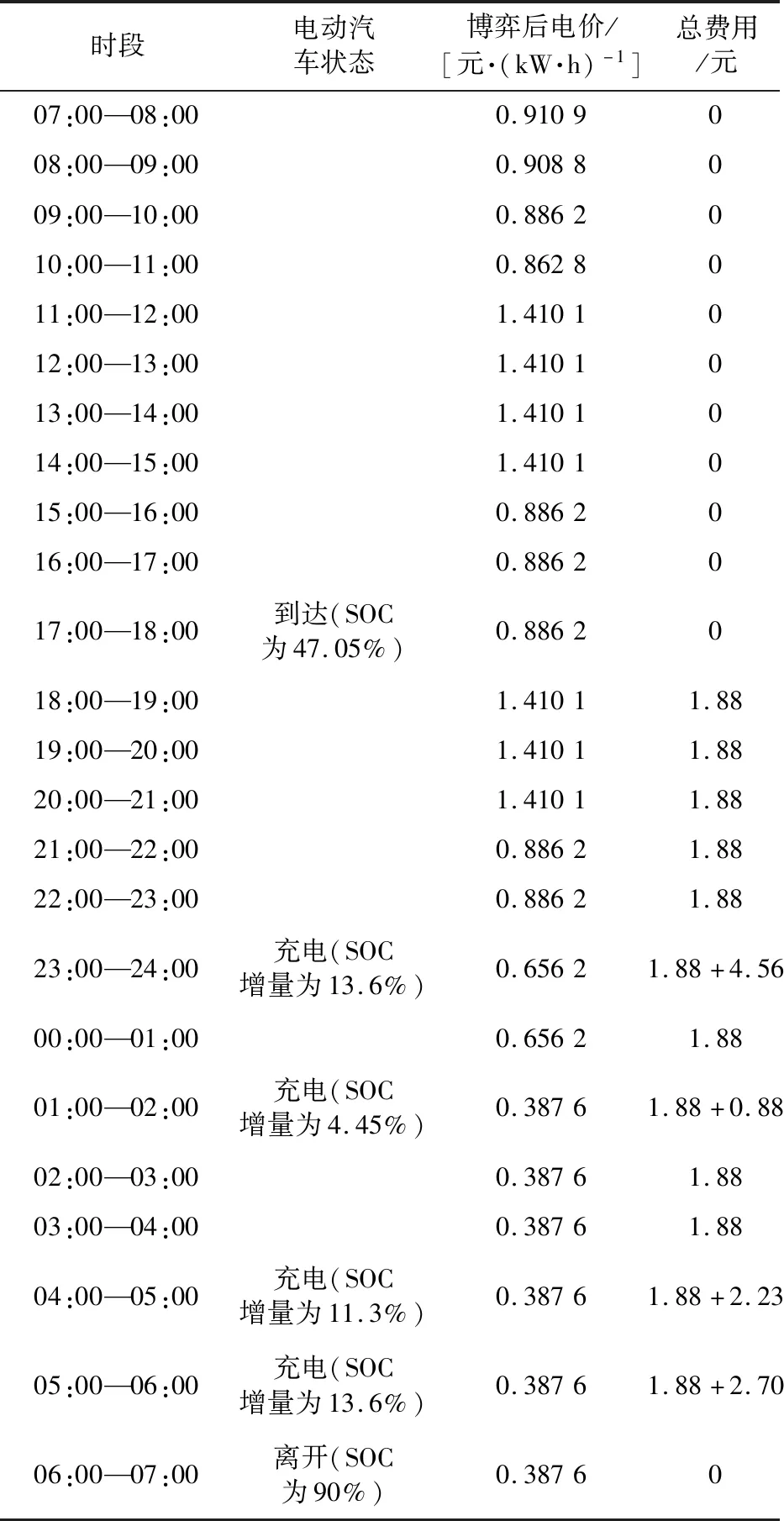
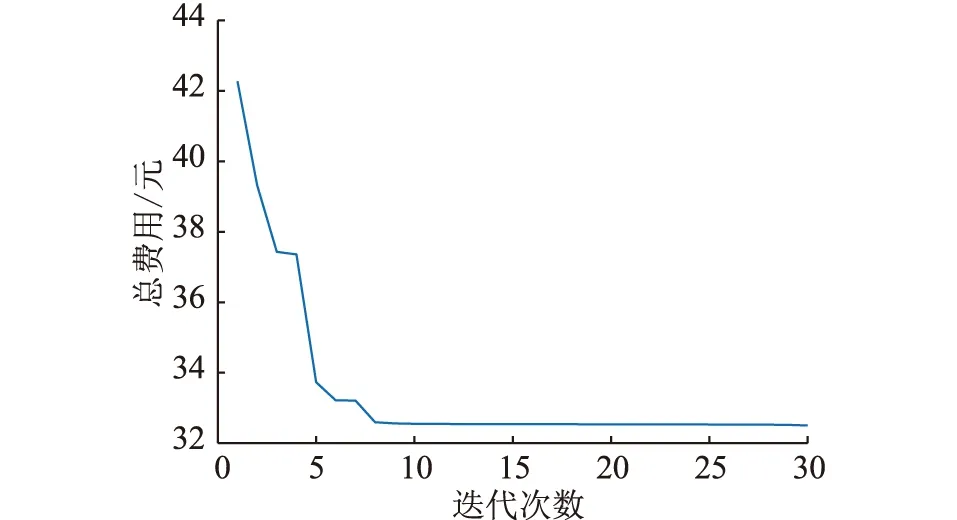
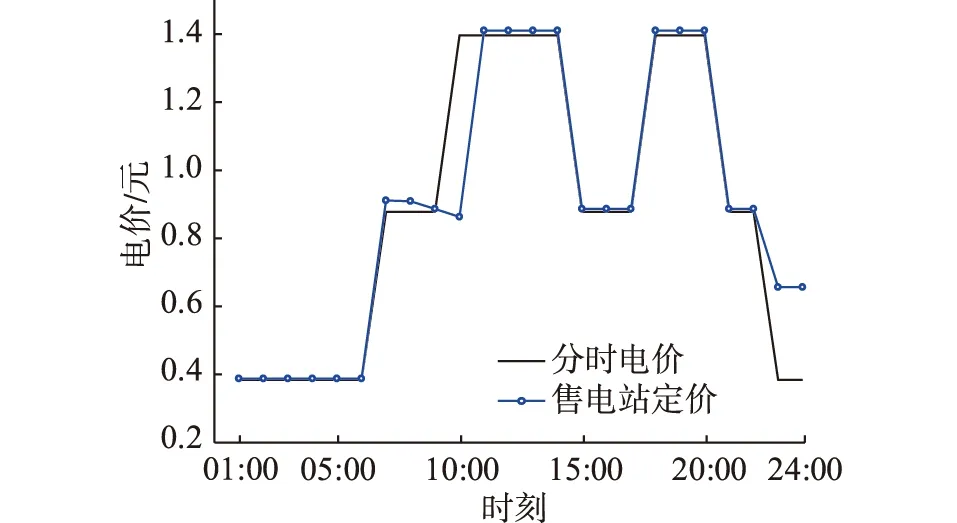
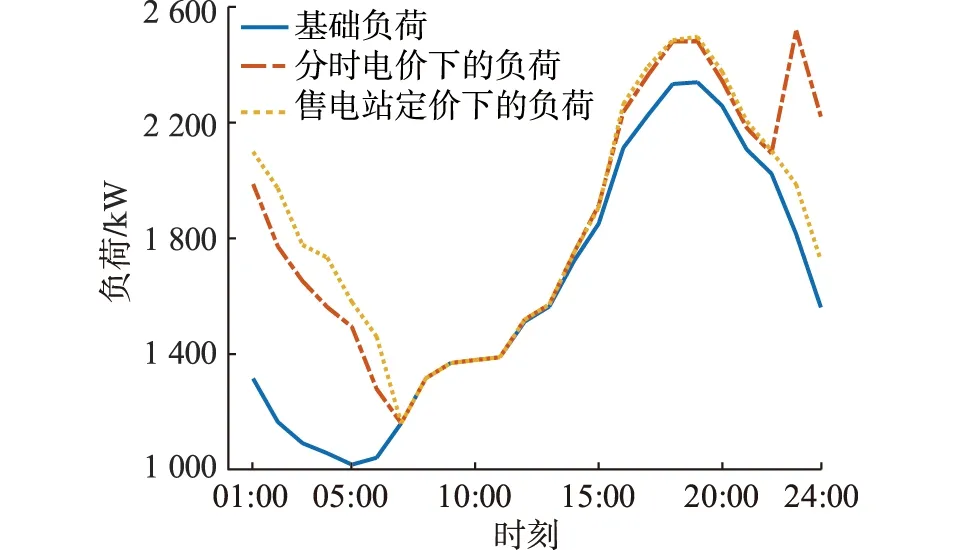
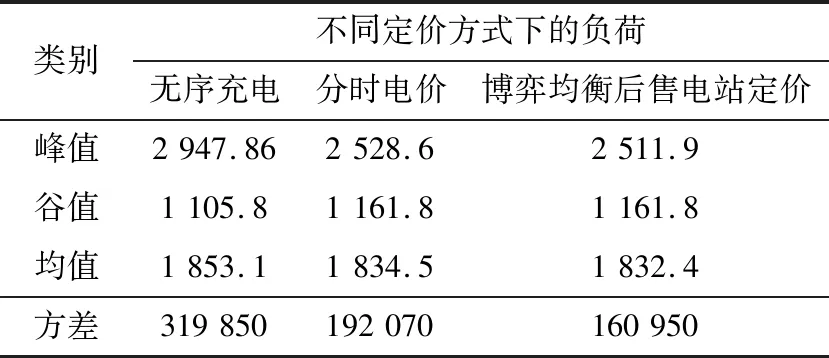
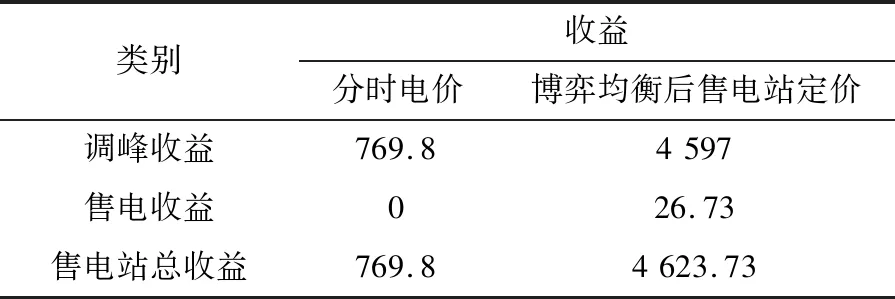
Pcommand,t+PEV,t (9) 2.2.3 售电方售电策略 售电方作为约束电动汽车充电时间、保证负荷曲线稳定在一定限度内的重要中介,其制定的电价既要约束大批量电动汽车同时接入充电,又要满足所有电动汽车的充电需求。售电站根据负荷曲线及表1中的分时电价制定电动汽车每小时的充电电价。 表1 分时电价Table 1 Time-of-use electricity price 当某时段负荷水平较高时,售电方在分时电价基础上抬高电价,抑制充电;负荷水平较低时,在分时电价基础上降低电价,鼓励用户充电。结合电价约束条件,可得: Pprice,t={Pmin,t,…,Pstart,t,…,Pmax,t} (10) 式中:Pstart,t为t时段电网制定的分时电价。 2.2.4 用户目标函数 为了使电动汽车用户获得良好的充电满足感,即相对便宜的充电价格和较短的充电等待时间。电动汽车用户的目标函数由充电成本和充电完成效益组成。一般来说,选择到达立即充电的用户充电费用较高,充电完成时间较短。选择响应充电策略的用户充电成本较低,充电完成时间较长。相应地,对于大部分电动汽车用户来说,目标是充电满意度最大。电动汽车n的充电金额f2,1,n为: (11) 式中:Plevel为充电效率,一般取0.88。 电动汽车n的充电完成效益f2,2,n由电动汽车接入时间tstart,n,充电结束时间tcomplete,n和接通充电桩时的剩余电量SSOC,n决定,即: (12) 综上,电动汽车用户的目标函数F2为: (13) 2.2.5 用户约束条件 为避免电动汽车电池极板损伤以及电池寿命缩短,需满足: (14) (15) 式中:Eneed,n为电动汽车n的可充电电量;Ebase,n为电动汽车n的电池总容量。 电动汽车的剩余电量不能超过电池容量,即: SSOC,min,n (16) 式中:SSOC,min,n,SSOC,max,n分别为电动汽车n电池剩余电量的最小值和最大值。 2.2.6 用户充电策略 为了最大化用户的充电满意度,用户需根据电价和充电所需时间及时调整充电策略。通过在配套的充电设施人机交互模式中添加最优化充电和立即充电模式选项,引导用户充电。使用户在高电价时段,一般选择不充电或者充少量电,在合适电价下,分散进入充电序列。电动汽车n的充电时间tdur,n为: (17) 式中:Pch,n为电动汽车n的充电功率。 则用户的充电时间策略集为: tdur,n={tstart,n,tstart,n+1,tstart,n+2,…,tcomplete,n} (18) 在PSO算法中,每个粒子代表一个可行解,通过粒子个体和群体内的信息交互,使粒子达到最佳位置[18]。将博弈双方的策略抽象为PSO算法中的粒子,利用PSO算法的速度和位置更新公式,求解双方的博弈策略,达到博弈均衡[19]。算法的位置和速度更新如下: (19) 式中:vi(m),xi(m)分别为粒子i在第m次迭代时的速度和位置;pbest,i(m),gbest,i(m)分别为粒子i的个体最优值和群体最优值;ω为惯性权重,取值区间为[0,1];c1,c2为学习因子;r1,r2为[0,1]间的随机数。 制定电动汽车充电策略和售电站电价是完成充电优化的前提。电动汽车连接充电桩后,系统通过电动汽车所需电量,预判充电时间。PSO算法根据当前负荷,模拟选取临近充电接入时间且电价相对较低的时段,制定充电策略,并生成新的负荷预测曲线。售电方根据负荷调整电价,重复进行上一轮策略模拟,直至售电站收益和电动汽车用户满意度综合最优。具体步骤如下: (1)对当天的基础用电负荷进行预测,初始化分时电价。 (2)根据居民区生活规律,导入电动汽车的到达时间和所需充电电量信息。 (3)种群信息初始化。生成种群大小为K的电动汽车用户和售电方的初始种群,分别记为KEV,Kcharge。初始化粒子的位置和速度,以变压器容量约束条件对电动汽车充电量进行限制,以售电站约束条件对充电电价进行限制。 (4)依据式(19)对粒子的位置和速度进行迭代更新。 (5)计算电动汽车用户目标函数,求解最优值。根据每小时电价求解满足约束条件且用户满意度最大化的粒子。 (6)基于博弈模型计算充电站目标函数,求解最优值。根据用户充电策略求解满足约束条件的收益最大化粒子。 (7)判断是否满足迭代终止条件,若不满足,转到步骤(4)重新计算,最终得到最优充电方案。 以深圳某住宅小区为例,模型参数为:居民用户600户,变压器最大负载能力为3 529 kW;居民小区内配有交流充电桩,充电功率恒为7 kW;电动汽车的电池容量为45 kW·h。假设:所有电动汽车均在当前居民小区内完成充电;居民小区内的电动汽车每天充满电后使用;居民小区内的充电桩可以支持数量足够多的电动汽车同时充电;电动汽车驾驶员的出门时间、行驶距离、返回时间均是相互独立的随机变量。 以1 h为间隔,对200辆电动汽车充电负荷进行仿真,验证文中所提有序充电优化方法的优越性。 在没有博弈的情况下,电动汽车充电的时间与人们正常生活工作的规律基本吻合。基于居民基础负荷,随机模拟电动汽车到达时间和行驶距离,不考虑分时电价,所有的电动汽车在到达后立刻连接充电桩充电,直至充满才断开连接。电动汽车无序充电下的负荷曲线如图2所示。 图2 无序充电下的负荷曲线Fig.2 Load curve under disorderly charging 由图2可知,电动汽车充电接入时段与电网的晚高峰时段基本重合,在15:00左右开始持续增长,18:00左右达到峰值。居民基础负荷和电动汽车充电负荷叠加,在17:00—21:00产生“峰上加峰”现象。随着电动汽车用户持续增加,负荷峰值将继续增大,容易导致变压器过载,不利于配电网安全运行。 电动汽车用户与售电站进行多轮博弈达到博弈均衡。某用户消费组成如表2所示。 表2 某用户消费组成Table 2 A user consumption composition 表2中,总费用为充电等待费用与充电费用之和。该用户1 d的总费用合计32.93元。用户在17:00左右到达,用户充电时除了考虑充电费用,还需考虑充电等待费用如停车费用等,表2中取1.88元/h。由23:00—24:00总费用可知,在电价较高时,充电费用明显大于充电等待费用,故用户在进行充电决策时,一般不会选择在电费较高的时段内充电,而选择电费相对较低的时段进行充电。该用户的充电决策迭代过程如图3所示。 图3 用户充电决策迭代Fig.3 User charging decision iteration 博弈均衡后售电站定价与分时电价对比如图4所示。由图4可知,售电站最终制定的电价在分时电价附近波动。17:00—21:00,进入充电等待的电动汽车较多,该段时间内电价都相对较高。相比之下,23:00—24:00电价明显降低,为降低充电成本,大批量用户会选择在该段时间进行充电。电动汽车集中充电会导致这2个时间段产生新的用电高峰,故23:00—24:00售电站电价略高于分时电价。在01:00—06:00,售电站电价略低于分时电价,可吸引大批量电动汽车用户在该段时间进行充电。 图4 分时电价与博弈均衡后售电站定价对比Fig.4 Comparison of time-of-use electricity price and game equilibrium selling power station price 以表1中的分时电价作为售电方基础定价,按照算法流程求得分时电价和博弈后售电站定价下的负荷曲线如图5所示。 图5 分时电价和博弈均衡后售电站定价下的负荷曲线对比Fig.5 Comparison of load curves under time-of-use electricity price and game equilibrium selling power station price 由图5可知,分时电价、博弈均衡后售电站定价下的负荷曲线与居民基础负荷曲线相似。与图2无序充电负荷曲线相比,二者均能在07:00前完成充电,不影响电动汽车用户的正常出行。分时电价虽然能在一定程度上抑制“峰上加峰”现象,但在居民用电高峰之后会出现电动汽车的充电高峰。博弈均衡后售电站定价下,第2个高峰消失,且不易超过变压器容量限制。值得注意的是,售电站电价下的负荷高峰并未消失,这是因为此时的电价水平已相对较高,且部分提早进入充电序列的高电量用户只有在此刻充电才能平衡充电等待花费和充电花费。 电动汽车在无序、分时电价、博弈均衡后售电站定价下充电的电网负荷情况如表3所示。 表3 不同充电定价下的负荷对比Table 3 Load comparison under different charging prices kW 由表3可知,相比无序充电定价下的负荷方差,博弈均衡后售电站定价下的负荷方差减幅为49.68%,分时电价定价下的负荷方差减幅为39.95%。售电站在寻求最大售电利益的同时兼顾电网侧负荷,电网负荷水平相比无序充电下的负荷水平明显改善。分时电价与博弈均衡后售电站实时定价的收益对比如表4所示。 表4 分时电价和博弈均衡后售电站定价下的收益对比Table 4 Income comparison under time-of-use electricity price and selling power station price 元 售电站参与电网调峰,减小负荷方差,获得调峰收益4 597元,相比分时电价下的调峰收益769.8元,增幅达到83%。可见,博弈均衡后售电站定价方式可以充分调动售电站参与调峰的积极性,避免负荷峰值持续升高。 同时,博弈均衡后售电站定价下用户的充电成本为5 606元,分时电价下的用户充电成本为5 518元。博弈均衡后的定价虽然在一定程度上增加了用户的充电成本,但能缓解分时电价下产生的充电高峰,保证电动汽车在07:00前完成充电,并在变压器容量限制下充分满足用户出行需求。 文中通过分析居民小区的出行规律和用电习惯,考虑用户的充电需求,建立了居民小区基本用电负荷模型,在此基础上提出了基于博弈论的电动汽车充电模型,并结合分时电价调节居民小区电动汽车用户充电行为。对某居民小区电动汽车充电时的电网负荷进行仿真,结果表明:在没有约束的情况下,电动汽车无序充电进一步加大了峰谷差,随着电动汽车数量增多,会影响配电网的安全可靠运行。而基于博弈论的电动汽车优化充电,降低了电网负荷方差,转移了负荷峰值,一定程度上改善了电压曲线,提高了电网的安全性。同时,所提控制策略考虑了电动汽车用户本身的出行、充电时长需求以及充电电价对负荷的影响,有效避免了新的负荷高峰出现。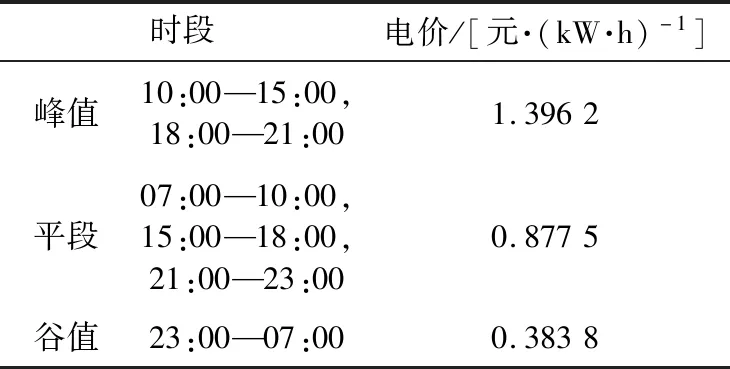
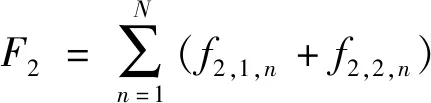
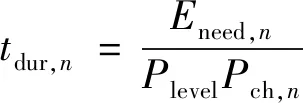
2.3 基于PSO算法的最优解求解
3 算例分析
3.1 仿真设置
3.2 无序充电仿真
3.3 博弈算法下的电动汽车优化充电仿真
3.4 算例结果比较
4 结语

