面向非完全理性用户的多元充电站优化调度策略
何胜利,刘现涛,张甜,陈中
(1.南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;2.国电南瑞南京控制系统有限公司,江苏 南京 211106;3.东南大学电气工程学院,江苏 南京 210096)
0 引言
截至2020年底,中国电动汽车(electrical vehicle,EV)保有量已达约500万辆。规模化EV的发展推动了交通与能源行业的融合[1—3],这不仅拓宽了电网的业务范围[4—5],也为含高比例可再生能源电力系统的随机性平抑提供了优质的用户侧资源[6—8]。
EV与电力系统融合的优化调度策略研究主要集中在2个层面:(1)合理调整EV充电的地点、时间和功率,减小规模化EV充电对配电系统负面影响,降低用户及运营商的用电成本[9—11]。(2)视EV群为分布式的储能系统,设计相应的调度及通信架构、优化算法和激励措施,为电网提供移峰填谷、频率调节等服务[12—14]。
用户行为对EV与电网融合有着深入影响,将成为信息-物理-社会融合系统中的重要环节[15]。在建模与优化控制的过程中,必须对非完全理性用户的决策行为进行研究[16]。期望效用理论(expected utility theory,EUT)是风险状态下用户决策的经典规范性理论,建立了不确定条件下对理性人选择进行分析的框架[17]。而前景理论(prospect theory,PT)将心理学研究应用在经济学中,由诺贝尔奖得主丹尼尔·卡内曼及其合作伙伴共同提出[18],是面向非完全理性人决策的描述性模型。
EV充电与分布式新能源(distributed renewable generation,DRG)具有潜在的协同性[19,且目的地充电是用作日常通勤的EV充电的主要方式之一[20],文中以含有DRG、常规负荷、储能的多元充电站(multi-element charging station,MCS)为研究场景。当前的研究中[21],往往将用户的充电需求作为约束条件,而对用户充电决策的主观性考虑不足。面向用户的激励机制较为复杂,缺乏直观性。
针对上述问题,文中设计了面向用户自主选择的价格机制,通过价格激励,引导用户为充电站的调节提供灵活性。并分别建立了基于EUT和PT的用户决策行为模型。同时考虑充电站运行经济性和面向电网的调节灵活性2个目标,采用模型预测控制(model predict control,MPC)方法,使得充电站运行优化能够兼容用户决策的随机性。基于合作博弈方法求解二者的平衡点,并通过虚拟变量的设置,将双层优化转化为单层二次优化。
1 价格机制设计与用户充电决策模型
1.1 充电价格机制设计
用户最终充电费用C决定方式如下。充电开始时,用户选择期望充电电量Q和能够接受的充电时长T,并计算预期的充电费用,如式(1)所示。
(1)

在用户离开前进行结算,设用户实际的充电持续时长为Tactual,则用户最终的充电费用为:
(2)
1.2 基于EUT的用户充电决策模型
EUT为规范性理论,即从客观角度出发,用户按此种方式进行决策能够实现利益最优。用户抵达充电站后,若选择T作为其充电时长,期望效用E(T)为风险条件下付出的充电成本的负值,可由式(3)进行计算。
(3)
式中:f(t)为充电持续时长的概率密度函数;E1(T),E2(T)分别为用户在设定时长达到之前、之后离开时所付出的充电成本的负值,二者之和为期望效用。用户选择使其期望效用最大的T作为其充电持续时长。
1.3 基于PT的用户充电决策模型
PT是用户在不确定性条件下进行决策的描述性模型。在PT的框架下,用户做出的决策未必是最优的。用户将选择前景值最大而非期望值最大的T,基于PT建立用户决策模型的主要步骤可以表示如下。
(1)参照点依赖。用户决策的载体是相对于参照点的收益或损失。用户选择Q,T后,将产生的C作为参考点。若用户提前离开,产生的损失为:
Lbefore=Qs(1-β(Q,T))
(4)
若用户推迟离开,产生的损失为:
Lafter=Qs(β(Q,T)-β(Q,Tactual))
(5)
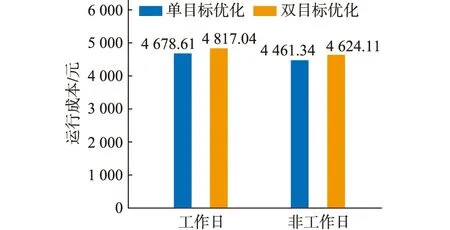
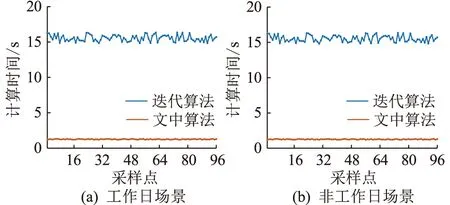
(2)框架效应。用户决策系统性的依赖前景的描述方式。选取Tactual,0,Tactual,1和Tactual,2作为用户可能离开的典型场景,Tactual,0 (6) 设L1 V(T)=L2ω(1-F(Tactual,2))+ (7) 式中:F(T),F(Tactual,1),F(Tactual,2)分别为用户在T,Tactual,1,Tactual,2前离开的累积概率密度;ω为概率的非线性变换函数。 (3)非线性偏好。PT框架下,用户会为小概率的事件赋予较大权重,而对中间概率事件p的变化不敏感,采用加权函数对概率进行非线性变换: (8) 式中:δ为损失规避系数,一般取值为0.2。 基于MPC的充电站调度优化的基本流程如图1所示,设每次优化的时间尺度为ΔT,执行时间步长为Δt,主要包括预测、优化、执行与滚动3个步骤。 图1 基于MPC充电站优化调度流程Fig.1 Optimization scheduling process of charging station based on MPC 首先,以Δt为步长,采用自回归滑动平均模型对DRG和常规负荷在当前优化时段Ti的值进行滚动预测;同时,对充电站未来时段的充电需求进行滚动预测,并根据用户行为决策模型预测用户选择的充电方案;然后,以当前优化时段Ti经济性最优、下一执行时段t2可用功率最大等为目标,以Δt为步长,计算当前时段Ti储能及EV的最优功率;得到最优功率计划后,仅执行时段t1的计划。并以Δt为步长向前滚动。 (1)优化目标。MCS的目标之一为其自身运行的经济性,而运营收入与MPC的效果无关,故在优化的过程中,采用运营成本代表其经济性目标: (9) 式中:Cobj(Ti)为当前优化时段充电站的运行成本;Ptotal(tj)为tj时段充电站的总功率;Eprice(tj)为tj时段的购电电价;βBE为储能充/放单位电量的损耗成本;PBEc(tj),PBEd(tj)分别为tj时段储能的充/放电功率。在短时间尺度的经济性优化中不考虑DRG的出力成本。 MCS的目标之二为其下一执行时段可上调功率,即其相对于计划功率可增加吸收的值最大化,反映了上级电网对充电站灵活调节能力的要求,可表示为: maxPobj(Ti)=max(Pt,max(t2)-Ptotal(t2)) (10) 式中:Pobj(Ti)为在下一执行时段的可上调功率;Pt,max(t2)为当前运行方案下时段t2能达到的最大功率;Ptotal(t2)为时段t2的原计划功率。 (2)约束条件。与EV相关的约束可表示为: (11) 式中:uEV,k(tj)为0-1变量,为1时代表第k辆EV在时段tj正在充电;UEV,k(tj)为时段tj的可充电状态,为1时代表其在时段tj可以充电,根据对用户充电行为的预测及用户的实际选择情况得到;PEV,k,min,PEV,k,max分别为第k辆EV的最小、最大充电功率;PEV,k(tj)为其在时段tj的充电功率;CEV,k,min(Ti),CEV,k,max(Ti)分别为时段Ti结束后的最小、最大充电电量。 与储能相关的约束可表示为: (12) 式中:uBEc(tj),uBEd(tj)均为0-1变量,uBEc(tj)为1代表储能处于充电状态,uBEd(tj)为1代表储能处于放电状态;PBEc,max,PBEc,min分别为储能充电功率的最大值、最小值;PBEd,max,PBEd,min分别代表储能放电功率的最大值、最小值;EB(tj)为时段tj储能的荷电状态;EB,max,EB,min分别为储能的最大、最小荷电量。 新能源出力与总功率相关的约束为: (13) 式中:Pnew(tj)为新能源出力;Pnew,predict(tj)为预测得到的新能源出力最大值;Pload(tj)为常规负荷的预测值;Ptotal,max为MCS受容量限制能够吸收的最大功率,设置Ptotal(tj)≥0。 MPC的目标1和目标2存在如下关系:目标2的优化是在已有运行计划基础上再次进行的,且仅当上级电网下发响应指令时才会执行,只影响之后的运行计划,而对目标1进行优化的时候,需考虑优化结果对目标2的影响。因此该优化是双层优化问题,为减少计算时间,满足在线滚动需求,文中采用如下方法处理目标1和目标2之间的关系。 记X(tj)为当前优化问题的控制变量,增设虚拟变量X′(tj),虚拟变量除满足式(11)—式(13)外,还需满足约束条件X(t1)=X′(t1)以保证下一执行时段调度计划的一致性。 同时,将优化目标2修改为: maxPobj(Ti)=maxP′total(t2)-Ptotal(t2) (14) 通过增设虚拟变量及相应约束条件,将双层优化问题转换为单层双目标优化问题进行求解。 由于MCS和电网处于长期稳定的合作关系之中,故可基于合作博弈的思想求该双目标优化的帕累托最优解。 (1)记目标1为Ψ1,目标2为Ψ2,分别求解Ψ1的最大值Ψ1,max和最小值Ψ1,min,Ψ2的最大值Ψ2,max,Ψ2的最小值记为0; (2)将目标1改写为: (15) 目标2改写为: (16) (3)加入权重变量d,将总目标记为: maxφ=max[(1-d)φ2-Cφ1] (17) 通过步骤(1)、(2)对目标函数进行规格化,并将权重作为优化变量以寻求最佳的配比。由此,将双目标线性优化转换为单目标二次优化,可通过成熟的求解器进行计算。 开展面向真实人的实验测试。受试者分为2组,分别由20名具备一定驾驶经验的学生和20名专业司机组成。实验流程如图2所示。 图2 面向真实人的充电行为决策实验Fig.2 Experiment of charging decision making for real people 首先设定实验人初始奖励。根据预设规律自动生成充电开始时刻、Q和预期离开时刻及其概率分布并告知实验人。有限时间内,实验人被鼓励按直觉设置T。之后,系统根据规则抽取Tactual并结算C。将初始奖励扣除C,作为本次实验的最终奖励发放给用户。开展2组对照实验。一组充电开始于日间,Q较少,T较短;另一组充电开始于傍晚或夜间,Q较多。β0取0.6,s取1.2元/(kW·h)。初始奖励为50元。 图3展示了PT和EUT的预测结果与实验人实际选择的对比。相较EUT,PT更为贴切地描述了用户的决策:EUT的预测结果平均相对误差为14.23%,而PT的预测结果平均相对误差为4.81%。面向专业司机和学生的实验结果没有明显差异。EUT在夜间长时间充电场景下的预测准确度明显提升,原因可能在于,用户对时间跨度较长的决策的风险敏感性有所降低。 图3 面向真实人的实验结果Fig.3 Results of experiments for real people EV进站流量、充电开始时刻、持续时长和充电电量等参数根据文献[22]中的方法生成。DRG容量为40 kW·h,常规负荷峰值为200 kW,采用文献[23]中的方法预测其出力及功率曲线。ΔT,Δt分别取1.5 h和15 min。充电桩数量为30,额定功率为21 kW。储能容量为20 kW·h,最大和最小的充放电功率分别为10 kW和1.4 kW,初始电量为容量的50%。峰(08:00—12:00,17:00—21:00)、谷(00:00—08:00)、平(12:00—17:00,21:00—24:00)等时段的电价分别设为1.07元/(kW·h)、0.31元/(kW·h)和0.64元/(kW·h)。采用PT预测用户的充电决策,根据3.1节的实验结果,以4.81%为平均值随机生成预测误差。基于Matlab平台,采用Yalmip工具箱调用Mosek求解器对模型进行求解,相关的运行环境为Intel(R)Core(TM)i7-9700 CPU@3.00 GHz RAM 32.0 GB。计算该充电站在工作日、非工作日2种场景下的调度结果,并与无序充电情况下的运行结果对比,如表1、表2所示。 表1 优化及仿真结果(工作日)Table 1 Optimization and simulation results on weekdays 表2 优化及仿真结果(非工作日)Table 2 Optimization and simulation results at weekends 无序充电情况下仅对储能运行进行优化。文中提出的优化调度策略在不同场景下均能有效降低运行成本达20%左右,并提供一定的功率灵活调节能力。特别是在非工作日,由于用户出行弹性大,优化调度策略的效果更为显著。 表1中,优化值是根据光伏、常规负荷和用户行为预测进行优化得到的结果,而仿真值是计及预测误差情况下执行决策变量优化值得到的结果。文中基于MPC的调度策略能够显著的抑制误差和随机性导致的优化结果劣化,仿真值与优化值的偏差控制在1%左右。 为进一步验证文中优化调度策略的效果,研究如下对比算例: (1)基于EUT预测用户的充电行为。工作日场景下充电站总功率优化值及仿真值如图4所示。对比算例中,由于未能较为准确的预测用户选择,总功率的优化值与仿真值之间存在较大偏差,优化得到的充电站日运行成本为4 701.65元,而运行成本的仿真值则为5 081.47元,文中调度策略下运行成本的仿真值则为4 817.04元。 图4 不同调度方法下充电站的运行情况Fig.4 The operation of charging station under different scheduling strategies 模拟上级调度于03:45下发功率上调指令,上调量为60 kW。文中调度策略下,充电站总功率准确跟踪了上级调度指令。而未考虑用户非完全理性行为的调度策略则未能完全满足上级调度需求。 (2)以站级经济性为单一目标进行优化调度。不同场景下,充电站运行成本对比如图5所示。单一优化目标下,工作日和非工作日运行成本分别为4 678.61元和4 461.34元。当采用文中的双目标优化方法时,增加运行成本小于4.0%,能够在经济性牺牲较小的情况下,提供站级调节灵活性。 图5 充电站运行成本对比Fig.5 Comparison of operating cost for charging stations (3)在双目标求解时,采用上下层迭代的方式进行。单次计算时间与文中所用方法的对比如图6所示。采用迭代方法时,单次计算时间在20 s以上,相同环境下,文中的求解算法大幅降低了求解时间,单次计算时间在1~2 s间,且在不同场景下保持了计算速度的稳定性,可满足在线优化的需求。 图6 计算时间对比Fig.6 Comparison of calculation time 文中将包含常规负荷、DRG及储能的MCS作为研究对象。设计了充电价格激励机制,在保证用户自由选择的基础上,挖掘其调节灵活性。并分别采用EUT和PT,建立了用户充电决策预测模型。基于MPC方法,通过合作博弈以及虚拟变量设置,对EV充电和储能的调度策略进行了多目标优化。真实人参与的实验结果表明,在面向不同对象时,考虑用户非完全理性的PT在描述用户选择上均更具优势。仿真实验结果表明,文中所提调度方法在不同场景下均能显著降低充电站运行成本,并以较小的经济代价为上级电网提供灵活调节能力,同时具备能够满足在线应用要求的模型求解速度。 与电力系统传统的调度对象不同,EV用户是分散的、具有非完全理性的个体。在进行EV与电网互动等工作时,应考虑社会-物理融合的模型。未来拟进一步开展面向城市级、多层次的EV充电优化调度研究。
L0(ω(1-F(Tactual,2)+F(T))-ω(F(T)))+
L1(ω(1-F(Tactual,1)+F(T))-ω(1-F(Tactual,2)+F(T)))2 基于MPC的充电站优化调度策略
2.1 调度优化的基本流程
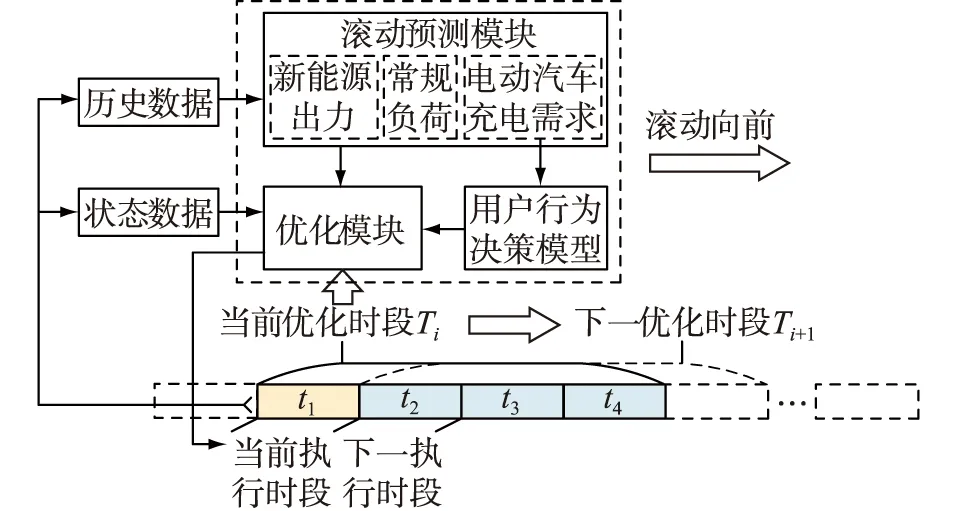
2.2 优化目标与约束条件
2.3 求解方法
3 实验及算例分析
3.1 理性人模型与非完全理性人模型的对比
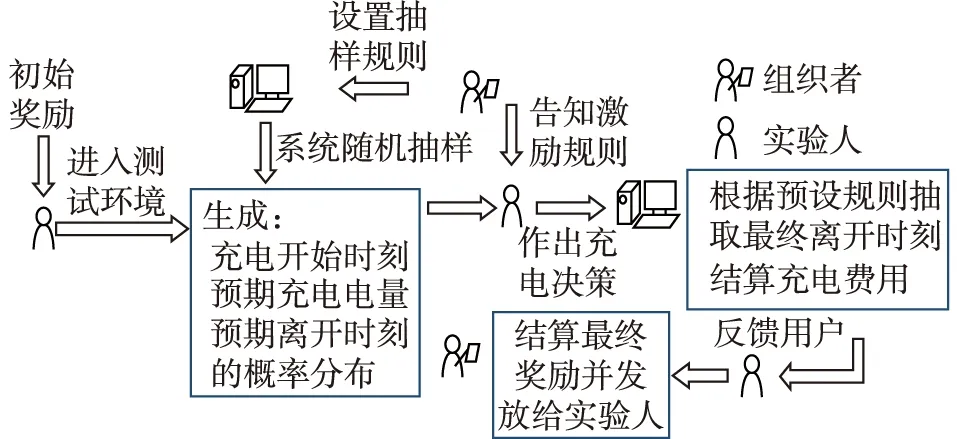

3.2 调度策略的有效性
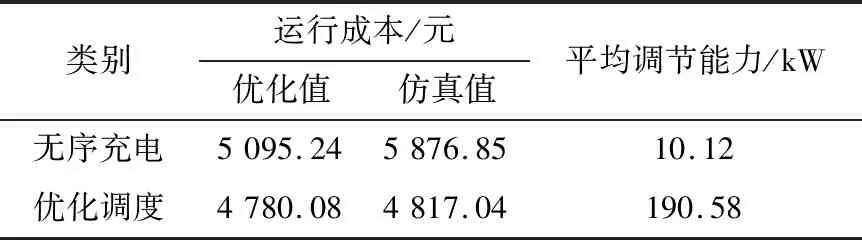
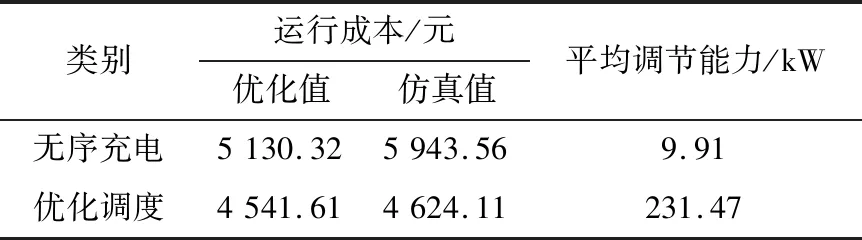

4 结语

