Hansen系数及其导数的直接计算方法∗

吴连大 张明江

(1 中国科学院紫金山天文台南京 210023)

(2 中国科学院空间目标与碎片观测重点实验室南京 210023)

1 引言

在天体力学的分析理论中,需要将摄动函数展开为时间和轨道根数的显函数,这涉及到两个最常用的特殊函数:倾角函数和Hansen系数[1].在卫星动力学中,地球引力场和日月第3体引力摄动的摄动函数展开即与Hansen系数有关[2–3].

Balmino[4]、Wnuk[5]、Giacaglia[6]、McClain[7]和Proulx等[8]给出了Hansen系数的各种直接计算表达式.利用这些Hansen系数的直接计算表达式,对轨道偏心率e直接求导,我们可以得到相应的Hansen系数导数的直接计算表达式.基于Hansen系数的定积分表达式及其直接求导的导数表达式,也可以实现Hansen系数及其导数的直接计算.此外,Wnuk[5]还给出了另一种Hansen系数导数的直接计算表达式.这样,对于Hansen系数及其导数的直接计算,本文回顾总结出7种主要方法:Balmino方法[4]、Wnuk方法[5]、Wnuk直接求导方法、Giacaglia方法[6]、两种McClain方法[7–8]和定积分方法.这些计算方法涉及的具体数学表达式,参见附录.需要说明的是,附录相关计算方法的数学表达式中,求和指标的符号遵照了原文献的形式,以便读者查阅原文.

本文针对这7种Hansen系数及其导数的直接计算方法,重点探讨各种方法的计算效率以及稳定性,进而得到一些有益的结论,为实际应用中Hansen系数及其导数的计算提供参考.

2 计算效率

为了比较分析,我们编制了这7种Hansen系数及其导数的直接计算方法的Fortran程序,包括:

(1) Balmino方法[4],即附录中表达式(1a)和(1b),其中指标t的求和限为0–50;

(2) Wnuk方法[5],即附录中表达式(2a)和(2b),其中指标s的求和限为0–70,指标t的求和限为−70至70;

(3) Wnuk直接求导方法,即附录中表达式(3a)和(3b),其中指标s的求和限为0–70,指标t的求和限为−70至70,注意附录中表达式(2a)和(3a)实质上是相同的;

(4) Giacaglia方法[6],即附录中表达式(4a)和(4b),其中,当指标时,指标s的求和限为0–70;当指标0时,指标t的求和限为0–70;

(5) McClain方法1[7–8],即附录中表达式(5.1a)和(5.1b),其中指标i的求和限为0–70;

(6) McClain方法2[7–8],即附录中表达式(5.2a)和(5.2b),其中指标i的求和限为0–70;

(7)定积分方法,即附录中表达式(6a)和(6b),使用分段两点Gauss积分方法,分段数为2000.

利用上述7种方法,计算偏心率函数Glpq=(l∈[2,30],p∈[0,l],q∈[−2,2],e=0.1)及其导数,各种方法的计算时间,如表1所示.计算设备的基本配置参数为:处理器Intel®Xeon®W-2125 CPU @ 4.00 GHz (8 CPUs),主频约4.0 GHz;内存32768 MB RAM.由表1可见,各种方法的计算效率差别很大,在具体使用时需要注意.另外,需要注意的是,目前本文中各种计算方法所采用的相应指标的求和限未必最优,读者在使用时应根据需要进行必要的数值试验,以确定指标合适的求和限.实际上,各种计算方法中指标的求和限选取,主要取决于偏心率的大小和需要计算的Hansen系数的阶次.

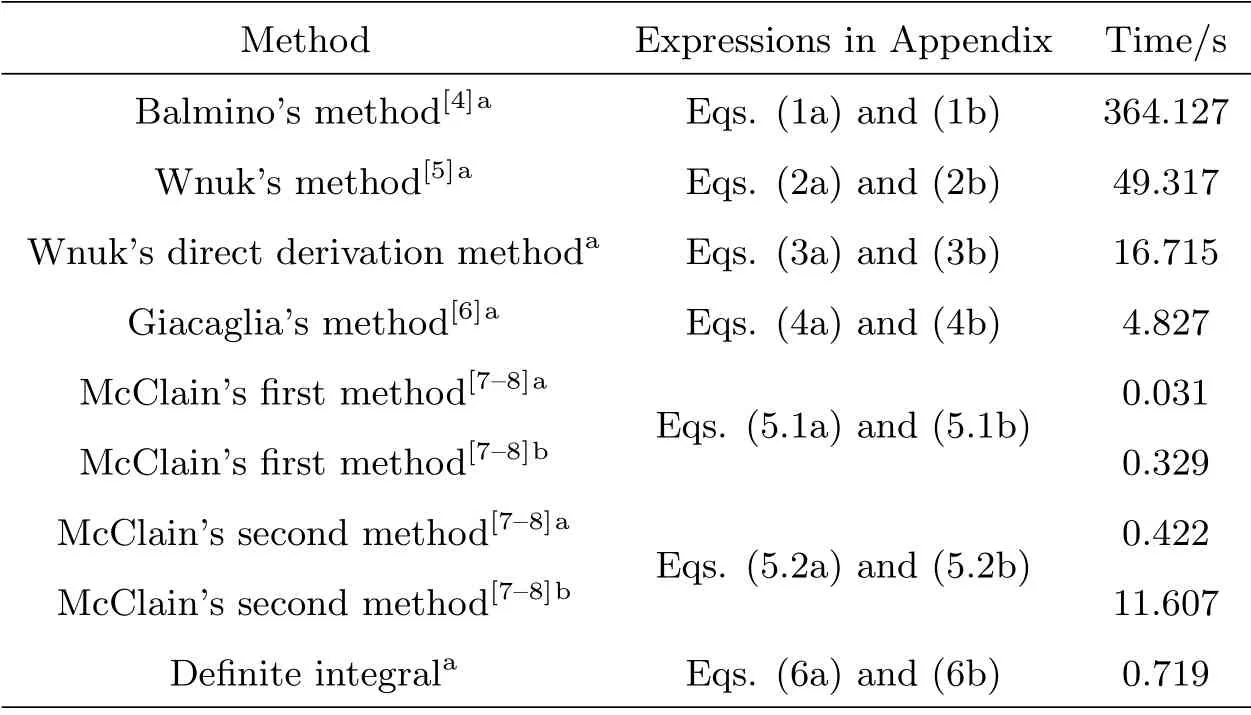
表1 各种方法的计算时间Table 1 Computing time of various methods

3 稳定性分析

Wnuk[5]对相关Hansen系数及其导数直接计算方法的稳定性,有过简约的评价:

(1)利用改造Bessel函数(渐近展开)算法的Wnuk方法,对应附录(2a)和(2b)式,是数字稳定的,对于偏心率e<1以及高阶l、p和q,能进行偏心率函数Glpq=及其导数的快速计算;

(2)Kaula方法[2](与McClain方法2本质上相同,对应附录(5.2*)、(5.2a)和(5.2b)式),对于大偏心率是数字不稳定的;

(3)定积分方法,对应附录(6a)和(6b)式,对于大偏心率e情形计算得很好,但由于计算时间和数字不稳定性,在实际应用中对高阶l、p和q的偏心率函数计算受到限制.

下面,我们结合上述7种Hansen系数及其导数的直接计算方法的Fortran程序计算算例,较深入地分析这些方法的计算稳定性.

3.1 Hansen系数计算的不稳定性例子

计算结果表明:对于小偏心率(e <0.2),各种方法计算均是稳定的.但是,对于大偏心率,Hansen系数计算会出现不稳定的情况.例如,对于偏心率e=0.6,Hansen系数的相关计算结果,见表2.

由表2中计算结果可见,对于Hansen系数的直接计算,Wnuk方法(Wnuk直接求导方法)和Giacaglia方法(即附录(3a)和(4a)式)的计算结果符合得较好(附录(2a)与(3a)式实质相同);定积分方法(即附录(6a)式)的计算结果与Wnuk方法、Giacaglia方法整体上一致.然而,Balmino方法和McClain方法1 (即附录中(1a)和(5.1a)式)的计算结果与Wnuk方法相比,从q≥−4开始就符合得不好了;McClain方法2 (即附录中(5.2a)式)的计算结果与Wnuk方法相比,从q≥6开始符合得不好了.计算表明:这些方法在大偏心率高阶的情况下,出现了不稳定的情况.这种不稳定现象的根源在于计算机字长不够,如果采用4精度计算,结果就稳定了.

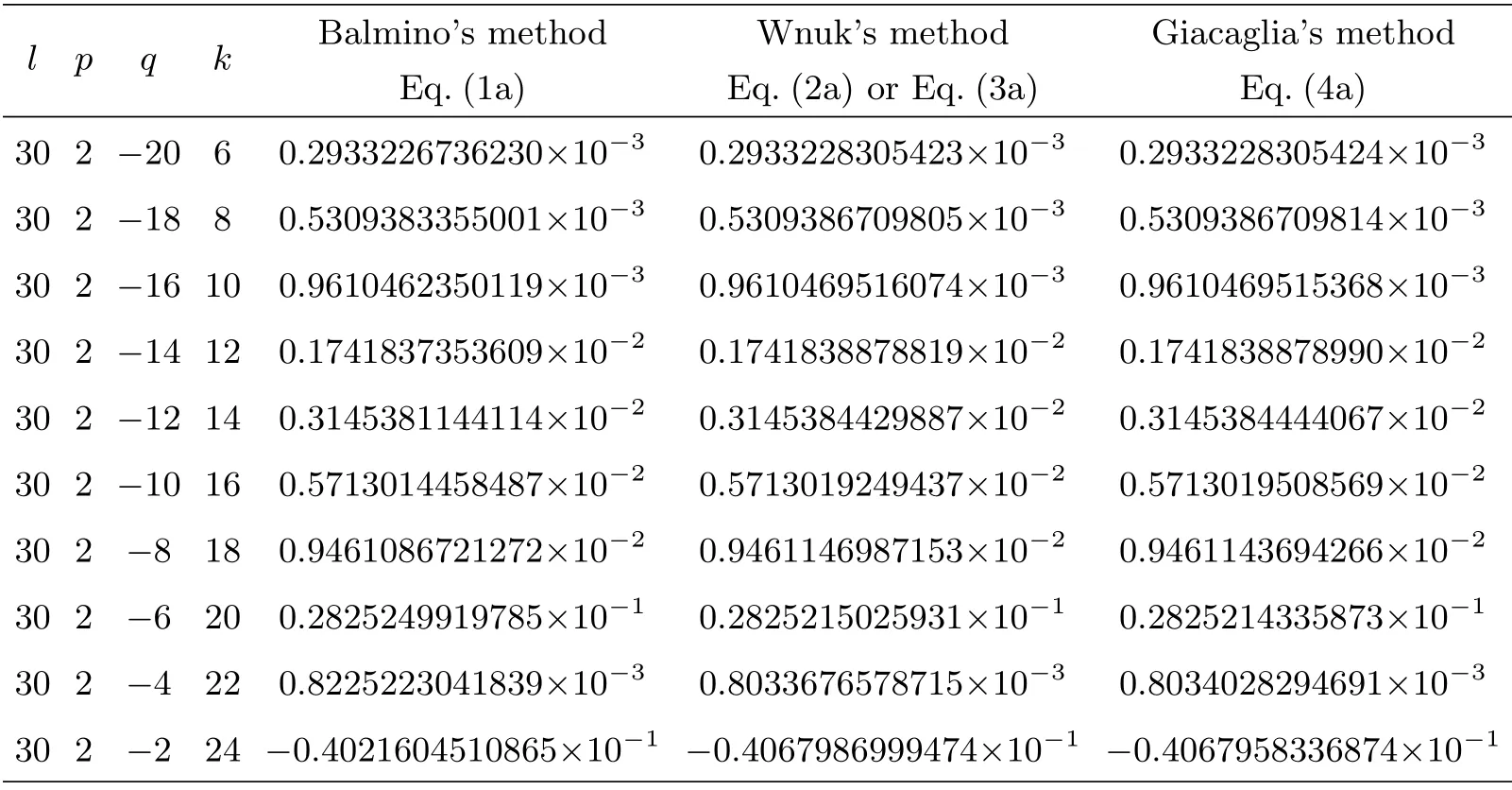
表2 Hansen系数计算算例(e=0.6)Table 2 The calculation example of Hansen coefficients (e=0.6)

表2 续Table 2 Continued

3.2 计算方法稳定性的判别

为了比较各种方法的优劣,需要一个判别计算方法稳定性的准则.实际上,利用直接计算方法计算得到的Hansen系数,通过判别这些数据是否满足Hansen系数的递推关系,就可判别方法的稳定性.

不难验证,对于小偏心率,各种方法的计算结果,均满足递推关系.但是,对于大偏心率,就不一定满足了.举一个例子,偏心率函数的递推关系式为[6]:

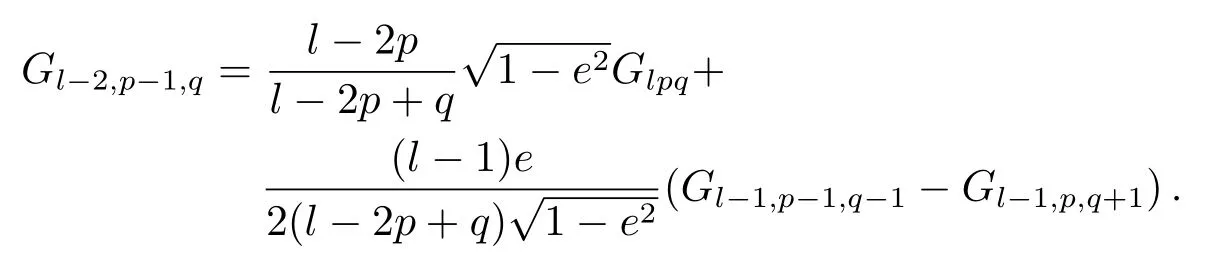
对于偏心率e=0.75,指标l=30、p=29和q=−1,Wnuk方法和McClain方法1,即附录(2a)和(5.1a)式程序计算结果,见表3.要判别Wnuk方法和McClain方法1的计算结果是否稳定,只需将计算结果代入上述递推关系式即可.对于Wnuk方法,此时Glpq=0.2056355791128×103、Gl−1,p,q+1=0.4210025874464×102、Gl−1,p−1,q−1=0.9079971968072×102、Gl−2,p−1,q=0.1542231019741×102;而l=30、l−2p=−28、l−2p+q=−29、l−1=29,于是递推关系式右边=94.5116409715.42231020 (递推关系式左边),显然这个结果不能认为是稳定的.对于McClain方法1,通过类似判别,相应的计算结果更不稳定.

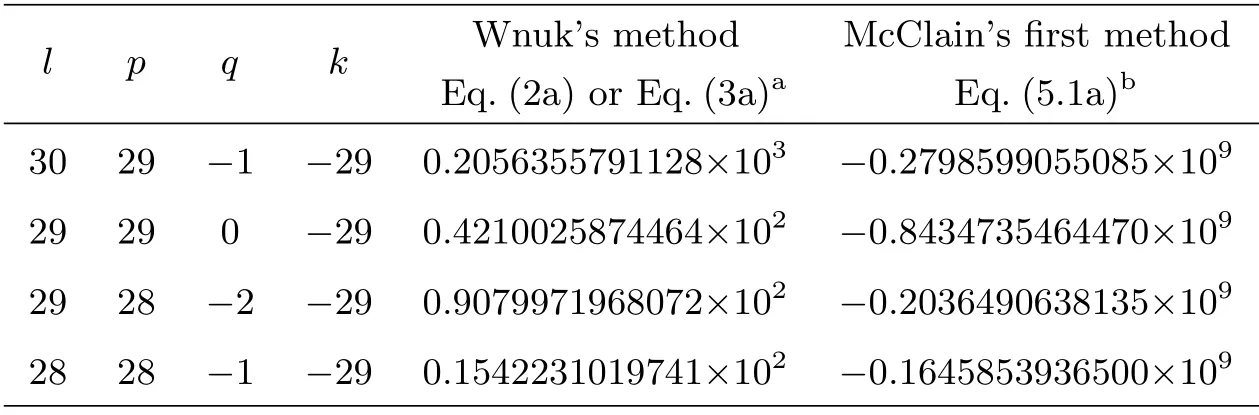
表3 稳定性判别数据(双精度计算)Table 3 The data for stability discrimination (double precision computation)

进一步分析表明,Wnuk方法的计算结果不稳定是由于求和范围不够,而McClain方法1不稳定是由于计算机字长不够.我们扩大Wnuk方法的求和范围,在McClain方法1中利用4精度计算,计算结果如表4所示.由表4可知,这两种结果可以认为是稳定的.应该说明,由于McClain方法1的计算效率很高,即使采用4精度来计算时间也较短,可以满足实用要求.

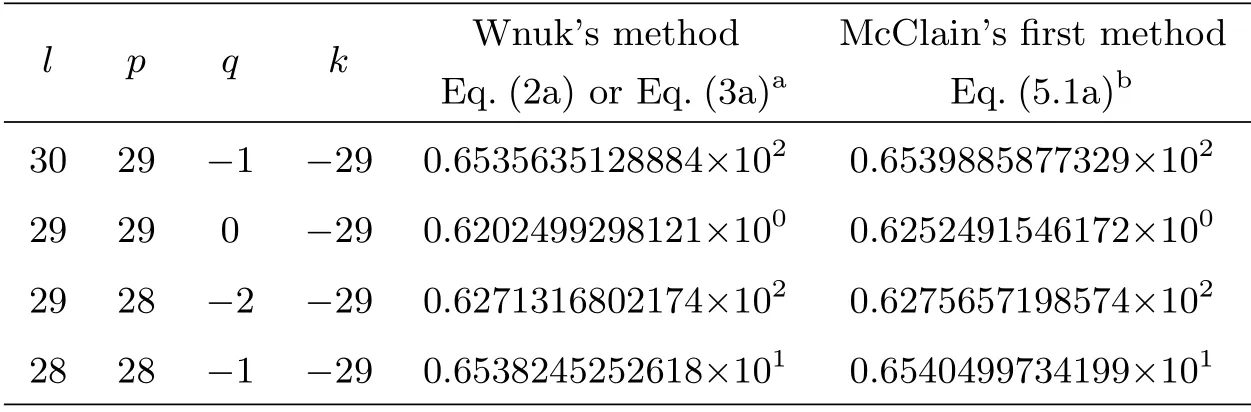
表4 稳定性判别数据Table 4 The data for stability discrimination

3.3 小结

根据7种Hansen系数及其导数直接计算方法的Fortran程序计算情况,结合上述分析,可以对Hansen系数计算,得出如下初步结论:

(1)对于小偏心率(e<0.2)轨道,各种计算方法均可以满足计算精度的要求;

(2)对于大偏心率轨道,Wnuk方法(Wnuk直接求导方法)和Giacaglia方法计算结果较好;

(3)可以利用递推关系来判别计算结果是否稳定;

(4)Hansen系数计算的主要困难是计算机字长不够.

Hansen系数计算不稳定的情况,均出现在大偏心率轨道情形,而小偏心率轨道没有问题.对于大偏心率轨道,分析Hansen系数计算丢失有效位数的原因,主要是由于Hansen系数计算,均是由级数求和得到,即y=∑xi.由于xi中含有阶乘和二项式系数,在偏心率较大时,其数量级相差很大,求和时会损失计算精度.最糟糕的是在求和时数量级大的数正负相消,余下部分(即为Hansen系数计算结果)是一个小数,如果这个小数比最大数的末位数值还小,计算结果就没有有效数字,不稳定问题就呈现出来.

由于大多数人造卫星采用小偏心率轨道,使用无奇点根数的摄动计算是必须的.针对无奇点根数的摄动计算,我们需要的是Hansen系数核,即须从Hansen 系数中提取e|k−m|因子,同时Hansen系数核本身不存在偏心率e为零的小分母问题.Wnuk方法,即附录(2a)或(3a)式,不能满足这一要求,不能计算Hansen系数核及其导数,因而不适用于无奇点根数的摄动计算.采用4精度计算的McClain方法1,即附录(5.1a)式,可以兼顾大小偏心率的Hansen系数计算,也许是较好的选择.

4 结论

本文回顾总结了7种Hansen系数及其导数的直接计算方法,给出了相关方法的直接求导的导数表达式,比较分析了这些方法的计算效率和计算稳定性.研究表明:Hansen系数的递推关系可以用来判别计算结果的稳定性.值得指出的是,Wnuk方法(双精度计算)和McClain方法(4精度计算)是稳定的,可以用来计算人造卫星轨道摄动.由于

大多数人造卫星采用小偏心率轨道,需要计算无奇点摄动,推荐使用McClain方法1 (4精度计算),即附录中(5.1a)和(5.1b)式.

附录

A.1 Balmino方法

基于Balmino给出的Hansen系数表达式[4],利用杨辉三角,我们得到下列Hansen系数的计算表达式:

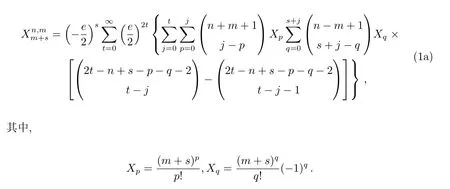
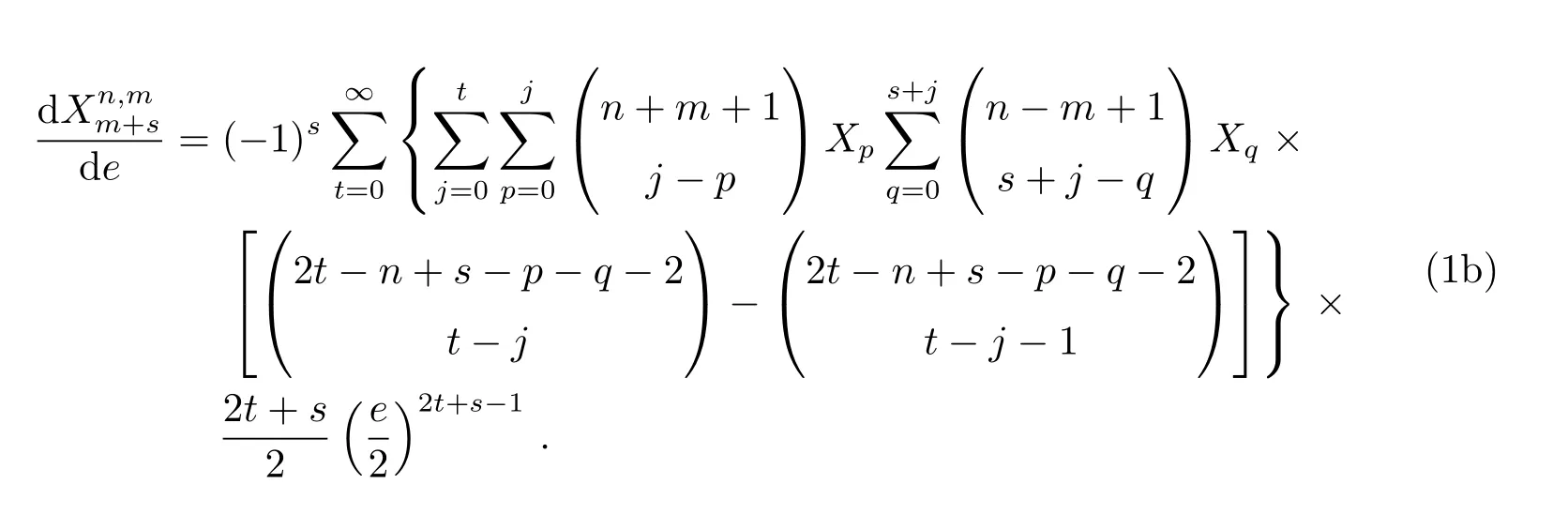
上述表达式(1a)和(1b)中,s必须恒为正.如果s <0,则利用Hansen系数的对称性进行计算,即表达式中的m和s均改变符号.

A.2 Wnuk方法

Wnuk给出下列Hansen系数及其导数的计算表达式[5]:

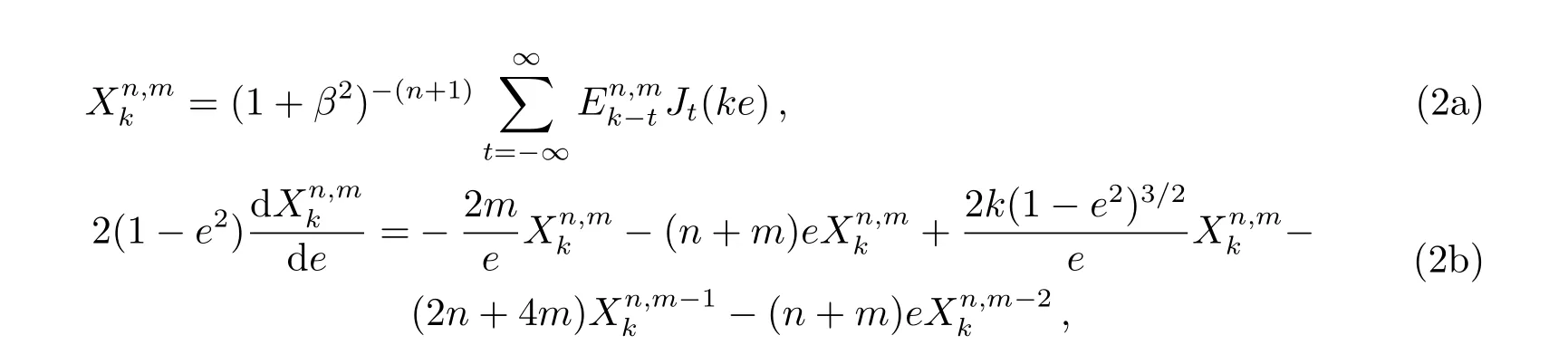
其中,

Jt(ke)是关于ke的Bessel函数.

Wnuk建议,按如下方法计算Bessel函数Jt(ke)[5,9]:

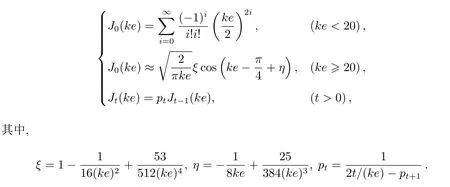
值得指出的是:J0(ke)有许多渐近展开式,上式中ξ和η的计算表达式引自文献[10],试算表明,这样计算J0(ke)的相当精度约为10−8,已能基本满足计算Hansen系数的要求;pt的递推计算,参见文献[9],从pt+1=0开始递推,取t=2N,N为需要计算的Jt(ke)的指标t的最大值;当ke=0时,上式中pt的计算有0分母,需要特殊处理.

当t<0或ke<0时,需用下式计算Bessel函数[9]:

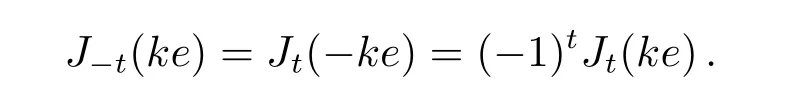
A.3 Wnuk直接求导方法

Hansen系数的计算表达式(2a)[5],可改写为如下形式:

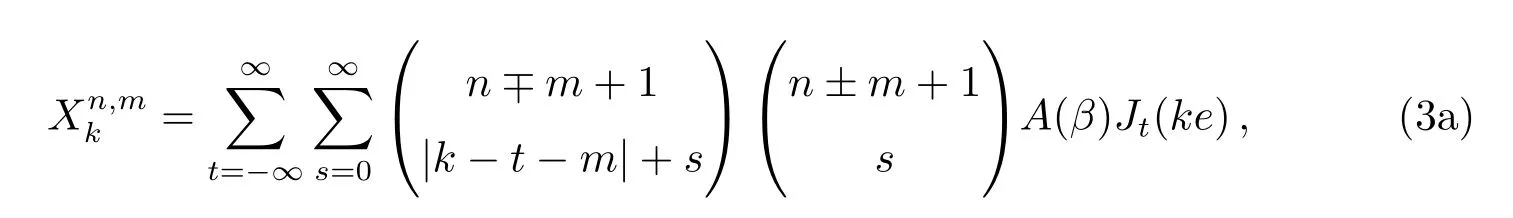
其中,m前的正负号可以根据k−t−m是否大于0来决定,

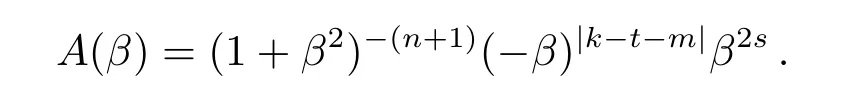
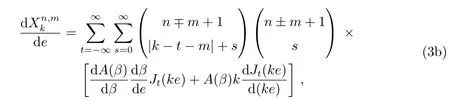
其中,

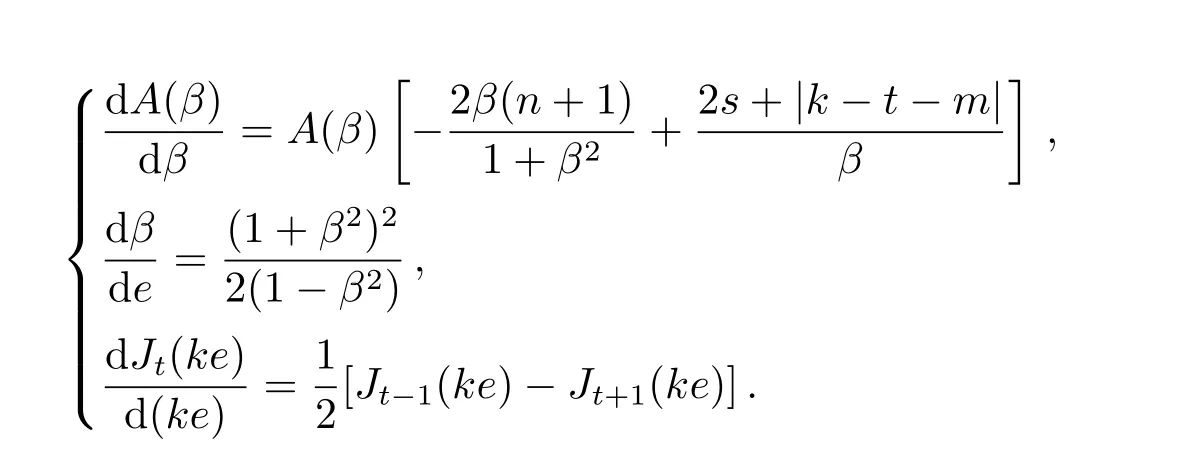
A.4 Giacaglia方法

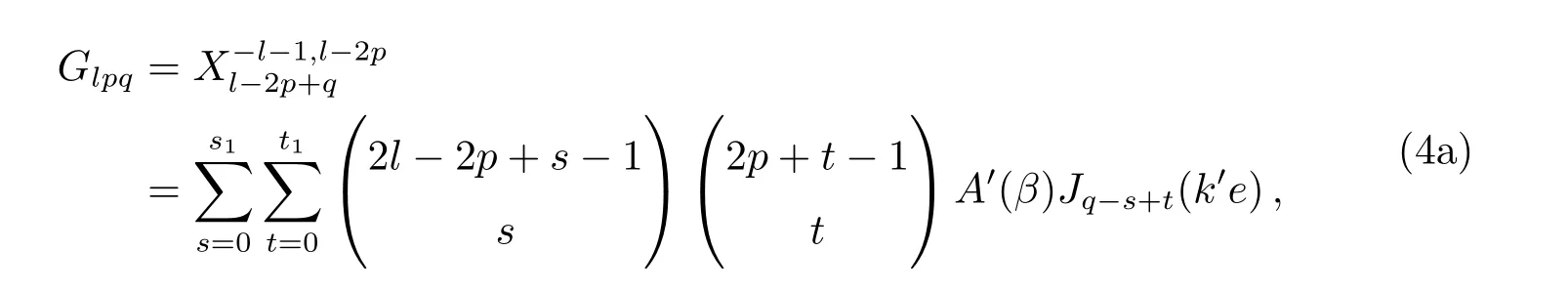
其中,

我们将(4a)式中偏心率函数Glpq,直接对轨道偏心率e求导,得到相应的偏心率函数导数的计算表达式:

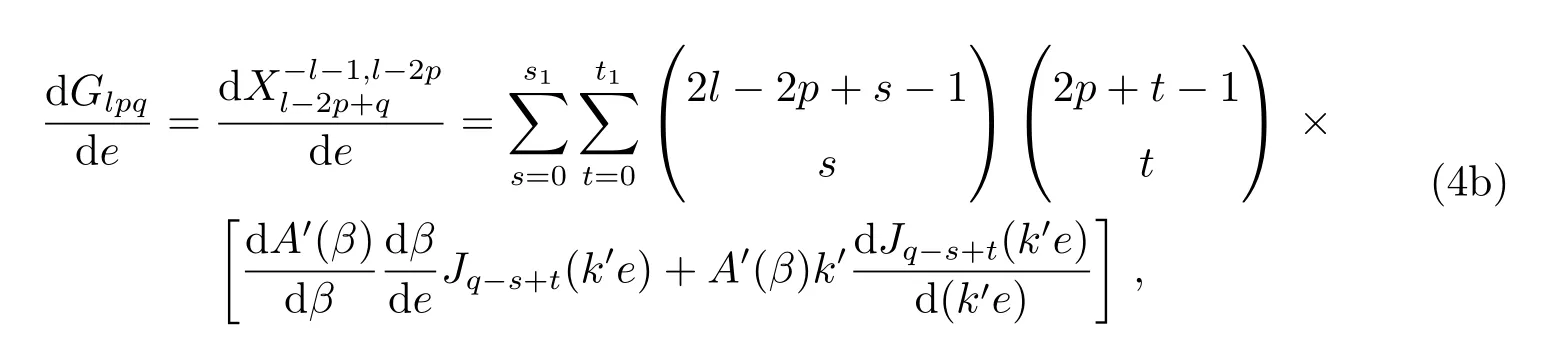
其中,

A.5 两种McClain方法

(1) McClain方法1

我们将(5.1*)式改写为下列形式,并将其对轨道偏心率e直接求导,有:

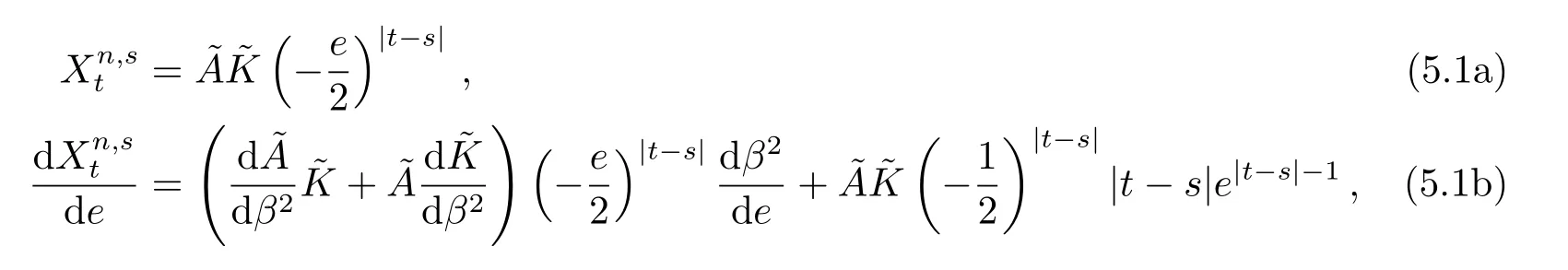
其中,

(2) McClain方法2

我们将(5.2*)式改写为下列形式,并将其对轨道偏心率e直接求导,有:

A.6 定积分方法

利用轨道偏近点角E作为积分变量,Hansen系数及其导数的定积分计算表达式为:

其中,r为目标向径,a、e、M和f分别为轨道半长径、偏心率、平近点角和真近点角.