基于AHP-TOPSIS 法的教学实验室综合评价与优选决策

林海斌

（台州学院 国有资产与实验室管理处，浙江 台州 318000）

0 引言

高校实验室是从事实验教学、科学研究、技术开发与社会服务的重要场所，是高校综合实力的重要体现，是高校物力、财力最集中的地方。教学实验室是高校应用型人才培养的重要基地，是对学生进行综合素质提高的重要阵地，也是从理论到实践过渡的重要桥梁，有利于培养学生的综合能力、严谨求实的科学作风、创新探索的精神［1］。随着对教育投入的加大，高校实验室的软硬件建设也日臻完善，但是高校实验室规划不科学、管理薄弱、安全隐患突出、实验室教学资源利用率不高、投入与产出效益比例较低等现象依旧存在，这些问题与高校实验室管理与评价的滞后有密切的关系。教学实验室综合评价是高校实验室管理和建设的重要环节，也是提高教学实验室建设质量与管理水平的有效措施之一［2］。建立和健全教学实验室综合评价体系与评价方法就显得尤为重要，目前关于高校教学实验室综合评价指标体系的研究比较广泛，但对评价方法研究并不多，更多的研究主要还是实验室的建设和管理问题［3－4］。因此，需要探索一套具有可行性、有效性的教学实验室评价模型，为实验室管理者对教学实验室综合考评提供理论依据与可操作性工具，促进教学实验室建设和管理水平的提高，具有现实的意义。

教学实验室的综合评价是一个多指标、多因素的复杂的评估过程。通过对影响教学实验室因素的梳理与分析，教学实验室综合评价的关键是评价指标的选取和评价方法的确定。目前，对高校教学实验室评价指标的选取和评价体系的确立，主要采取层次分析法（AHP）［5－11］。这种评价方法采用定性和定量确定各评价因素的权重，建立评价模型，对实验室的绩效水平做出综合评估，虽然在实验室综合评价方面取得了一定的效果，但层次分析法仍存在不能为决策提供新方案、特征值和特征向量以及精确求法比较复杂等不足［12－14］。逼近理想解排序法（TOPSIS）［15－17］具有运用灵活、评价合理、对样本无特殊要求、能充分利用原有数据信息、与实际较为吻合、能对评价对象的优劣进行排序的优点，本文将AHP 法与TOPSIS 法相结合，先利用AHP 法对影响指标进行分层别类，确定指标权重，然后结合TOPSIS 法建立高校教学实验室综合评价的决策模型，并对教学实验室综合状况的优劣进行决策排序，为管理者对教学实验室科学规划、合理投入、持续建设和发展提供决策依据。

1 教学实验室综合评价指标体系的建立

1.1 评价指标制定的原则

教学实验室综合评价的指标有很多，要选取具有代表性和能反映实验室情况的关键指标，因此在制定指标体系时应遵循几个原则［18］。（1）指标遵循特定性原则，要把教学实验室与科研实验室区分对待，指标要突出教学实验室的特点，既要考虑评价指标的客观性又要考虑它的竞争性，不但要求全面还应具有可比性、易于量化计算。（2）遵循客观性原则，要体现实验室的本质和特征，收集评价的佐证材料要具有真实性和准确性，实事求是地进行评估，评价结果应该做到客观、公正。（3）遵循指导性原则，评估目的在于，通过评估促使各实验室了解在建设、使用、管理过程中存在的问题与差距，不断提高管理水平。

1.2 评价指标体系的建立

在文献［18－22］研究的基础上，结合对教学实验室管理的调研总结和对众多评价指标归纳分类进行筛选和分析，最终确定教学实验室综合评价指标体系由实验室管理、实验教学管理、资产管理、实验队伍管理、环境与安全、管理制度等6 个一级指标（准则层）和26 个二级指标（指标层）组成，如表1 所示。

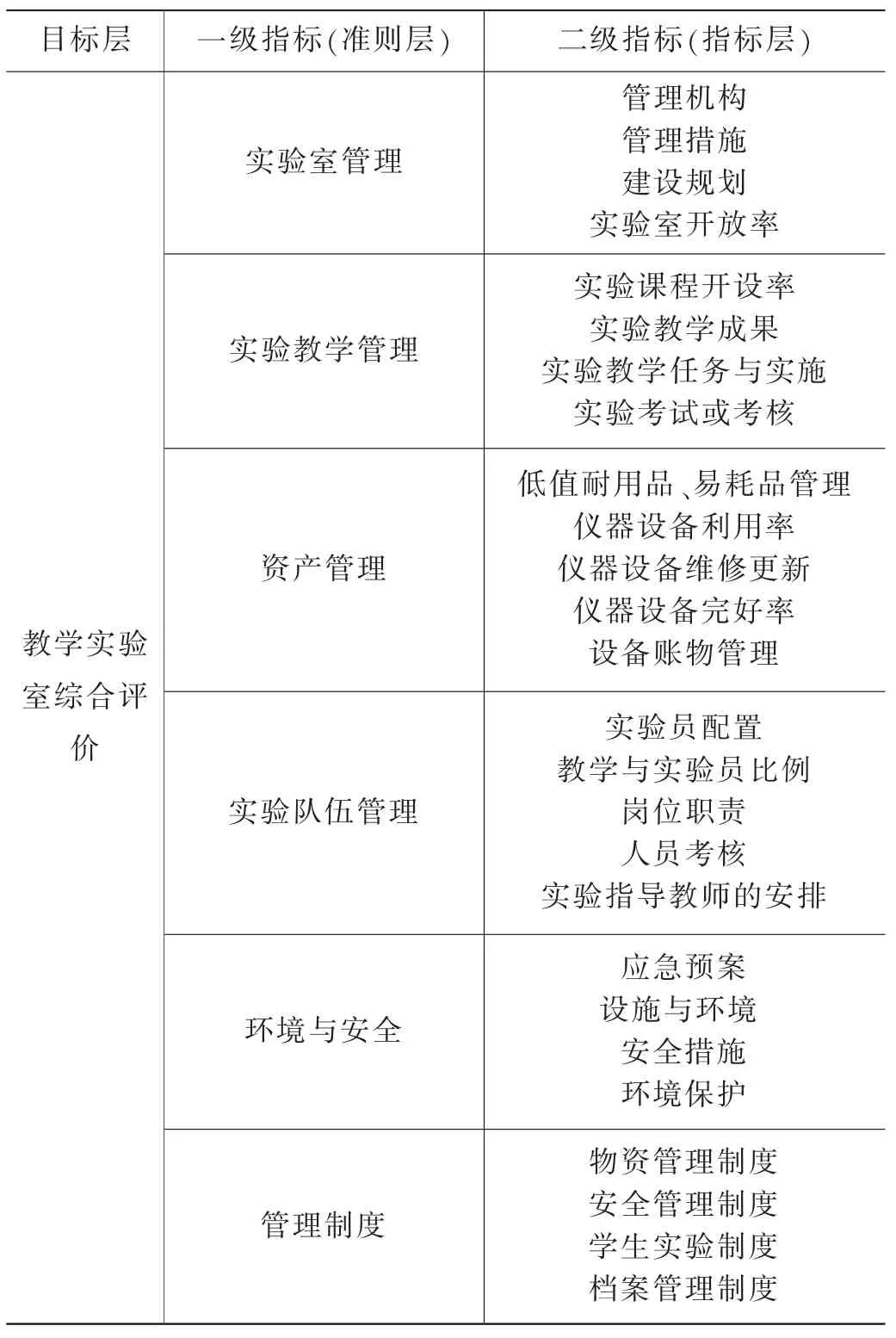
表1 教学实验室综合评价指标体系

2 AHP－TOPSIS 法评价模型的研究

2.1 AHP 法确定权重

（1）构造判断矩阵

构建第一层目标层、第二层准则层、第三层指标层的三个层级评价指标体系，以上一层中的某一指标作为评价准则，对本层的指标进行两两比较来确定相对重要程序，用数字1～9 以及其倒数来确定矩阵元素，构建判断矩阵A［23］。

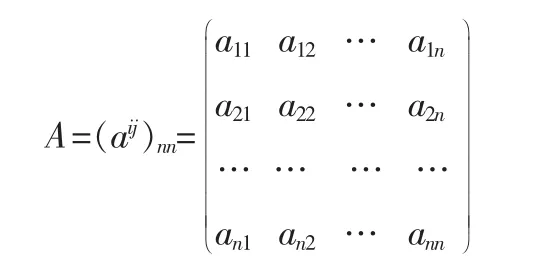
式中n 是指与上一层某准则相关的该层因素的个数，aij选取依据是表2 所表示的模糊标度。

表2 模糊标度及其含义

A 中的每行元素连乘并开n 次方

（2）一致性检验

对判断矩阵A 的特征根求解（AW=λmaxW）得到特征向量W，经过归一化后，成为属性的排序权重。

为避免权重产生误差，使判断矩阵的结果更符合实际，需进行一致性检验，一致性指标为，n 为判断矩阵的阶数。对于1～9 阶判断矩阵的平均随机一致性RI 的值见表3。

表3 1～9 阶判断矩阵的平均随机一致性指标RI

2.2 构建AHP－TOPSIS 模型

TOPSIS 法是一种距离综合评价法，也称为逼近理想解排序法。这种方法的特点是借助于多目标决策问题的“理想解”和“负理想解”进行方案排序。“理想解”与“负理想解”是基于标准化后的原始数据矩阵中设想的一个最优或最劣的方案，然后获得某一方案与最优方案和最劣方案间的距离，从而得出该方案与最优方案的接近程度，依据相对接近度的大小对评价结果排序。TOPSIS 法通过对原始数据进行同趋势和归一化处理，消除了不同指标的量纲影响，能客观反映方案间的真实差距，应用广泛［24－26］。

（1）建立决策矩阵

假定对被评价N 个方案的P 个指标进行综合评价，建立多方案、多指标属性决策矩阵，见表4。

表4 多方案多指标属性决策矩阵

将标准化后的决策矩阵中的每一列与运用AHP 法得到的各个因素的权重Wi相乘得到矩阵

（2）确定正负理想解及计算接近距离

正理想解Z+：Z+=（Z1+，Z2+，…，Zp+），其中Zj+=max（WjZ1j，WjZ2j，…，WjZnj）j＝1，2…，p

负理想解Z-：Z-=（Z1-，Z2-，Zp-），其中Zj-=min（WjZ1j，WjZ2j，…WjZnj，）j＝1，2，…，p

计算正、负理想解之间的欧氏距离：

式中Di+为方案与正理想解的距离，Di-为方案与负理想解的距离。Zj+为正理想解的第j 个分量，Zj-为负理想解的第j 个分量。

（3）确定决策方案与正理想解的接近度

Ci值在［0，1］区间变化，Ci值越接近1，说明决策方案越接近理想方案。

（4）综合评价

将评价方案到正理想解的接近度矩阵Ci进行排序，就可以确定决策方案的优劣顺序，Ci越大，方案则越优。

3 实例应用

以某地方高校2018 年对制药化工实验教学示范中心的7个建制教学实验室（①材料工程实验室；②基础化学实验室；③高分子材料实验室；④分析测试实验室；⑤化学工程与工艺实验室；⑥3D 打印实验室；⑦制药工程实验室）综合评价分析为例。邀请校内外10 位实验室管理专家通过听取汇报、查阅资料、现场考察等形式对7 个建制教学实验室按上述教学实验室评价指标体系中的6 个一级指标、26 个二级指标进行评价，二级指标按优90 分、良75 分、中60 分、差45 分四个等级进行评定后换算成算术平均值。实验室管理专家评定结果换算成算术平均值统计如表5 所示。

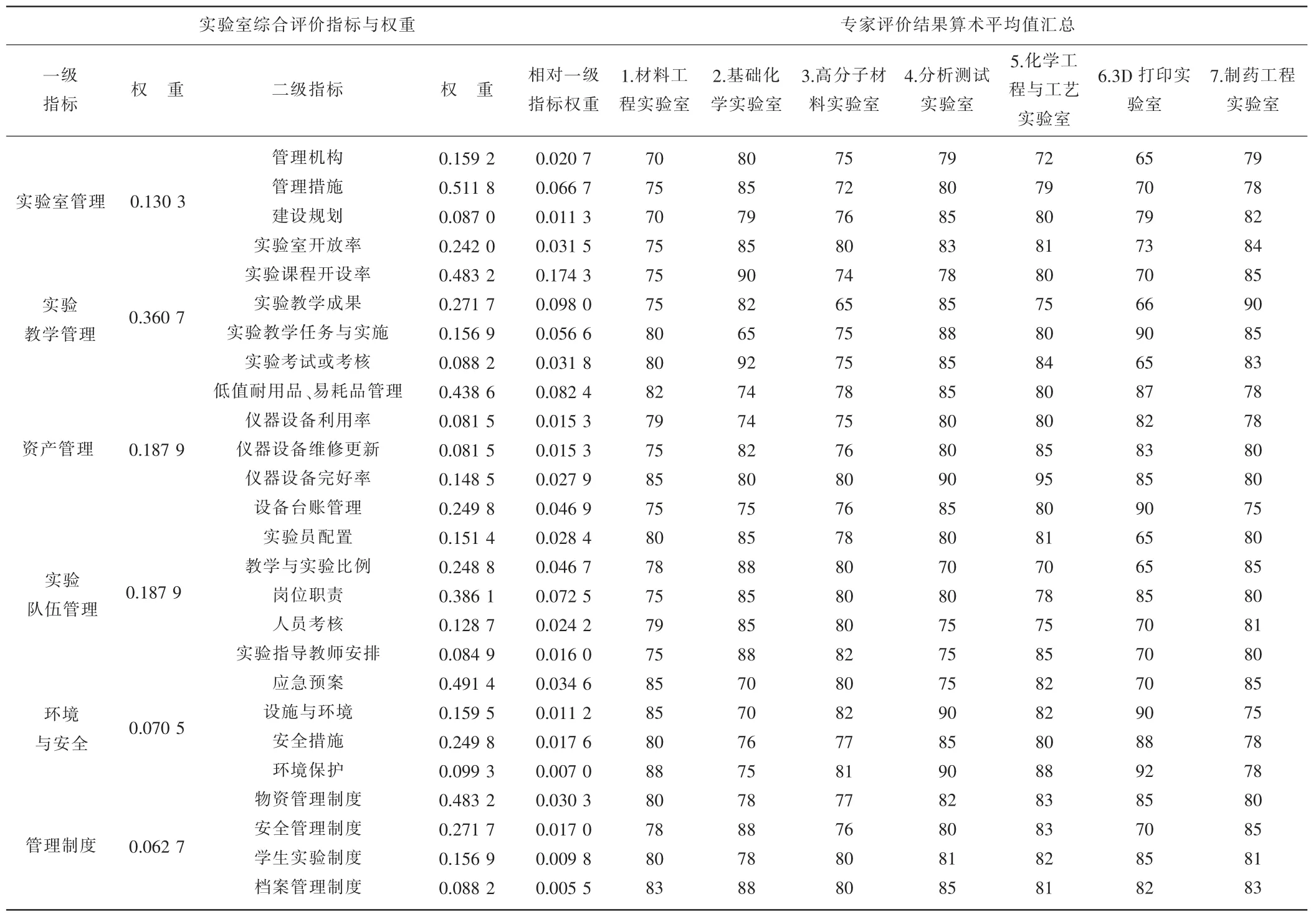
表5 10 位专家对7 个建制教学实验室评价结果统计表

3.1 AHP 法确定教学实验室各评价指标权重

以问卷调查及专家访谈形式对教学实验室评价指标中的6 个一级指标、26 个二级指标的重要性进行两两比较。6 个一级指标建立起判断矩阵如下：

根据公式（1）（2）计算出6 个一级指标的权重，结果为w1＝0.130 3，w2＝0.360 7，w3＝0.187 9，w4＝0.187 9，w5＝0.070 5，w6＝0.062 7

根据公式（3）（4）计算λmax，λmax＝6.069 7

同理可得出：一级指标“实验室管理”下面的4 个二级指标的权重为w1＝0.159 2，w2＝0.511 8，w3＝0.087 0，w4＝0.242 0；“实验教学管理”下面的4 个二级指标的权重为w1＝0.483 2，w2＝0.271 7，w3＝0.156 9，w4＝0.088 2；“资产管理”下面的5 个二级指标的权重为w1＝0.438 6，w2＝0.081 5，w3＝0.081 5，w4＝0.148 5，w5＝0.249 8；“实验队伍管理”下面的5 个二级指标的权重为w1＝0.151 4，w2＝0.248 8，w3＝0.386 1，w4＝0.128 7，w5＝0.084 9；“环境与安全”下面的4 个二级指标的权重为w1＝0.491 4，w2＝0.159 5，w3＝0.249 8，w4＝0.099 3；“管理制度”下面的4 个二级指标的权重为w1＝0.483 2，w2＝0.271 7，w3＝0.156 9，w4＝0.088 2。

3.2 建立归一化处理的数据矩阵

相乘得到归一化后的矩阵Z：

根据公式（5）得出与各个二级指标相对一级指标权重Wi

3.3 确定指标最优值和最劣值

确定指标最优值和最劣值，分别构成最优值向量和最劣值向量，即被评价七个建制教学实验室的最优方案和最劣方案为：

3.4 评价指标值与最优值和最劣值的距离

根据公式（6）（7）计算方案与正负理想解之间的欧氏距离，得出各评价指标与最优值和最劣值的距离为D1+=0.016 7，D2+=0.045 1，D3+=0.016 5，D4+=0.025 7，D5+=0.020 2，D6+=0.027 3，D7+D2+0.018 1；D1-=0.043 8，D2-=0.021 5，D3-=0.040 0，D4-=0.028 0，D5-=0.036 9，D6-=0.031 3，D7-=0.041 3。

3.5 计算相对接近程度

根据公式（8）计算与正理想解的接近度，得出C1=0.724 0，C2=0.322 8，C3=0.708 0，C4=0.521 4，C5=0.646 2，C6=0.534 1，C7=0.695 3。

3.6 建制教学实验室综合评价优劣排序

根据Di+、Di-、Ci计算值，排序结果见表6。

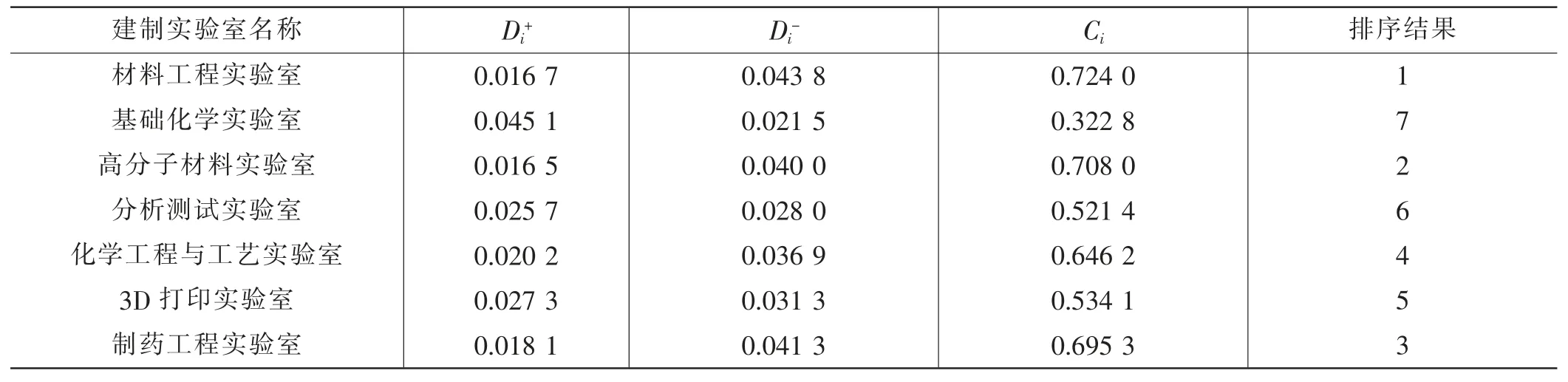
表6 建制教学实验室评价指标值与最优值接近程度及排序结果

从表6 可知，建制教学实验室综合评价的结果以材料工程实验室综合评价最优，其次为高分子材料实验室，基础化学实验室综合评价最差，评价结果与实验室事实状况基本相符。因此，实验室管理部门可以依据评价结果，分析问题存在的原因，有针对性地采取整改措施，促进实验室管理水平的提高。

4 结语

本文提出了基于AHP－TOPSIS 法的教学实验室综合评价方案优选决策模型，采用层次分析法确定指标权重，有效解决了评价指标间相互依赖与反馈关系，避免了人为赋予权重主观性和片面性的影响。AHP－TOPSIS 法的教学实验室综合评估可以促使各教学实验室具体了解在实验室建设、使用、管理过程中存在的问题与差距，不断提高实验室管理水平。为管理者对实验室科学规划、合理投入、持续建设与发展提供决策理论依据和一套切实可行的评价工具。

用AHP－TOPSIS 法对教学实验室综合评价具有原理简单、易于理解、结论直观等优点，是在TOPSIS 法评价基础上的升级改良，是综合评价的有效方法，为开展在其他领域进行评价提供了新的思路与方法。