从图形运动看全等三角形
第一章 全等三角形
领 衔 人:王金坤
组稿团队:江苏省盐城市毓龙路实验学校
在以前的学习活动中,我们常常将一个图形平移、翻折、旋转,以此来进一步认识图形的性质。图形的平移、翻折、旋转统称为图形的运动。图形的运动不改变图形的形状、大小,也就是说,运动前、后的两个图形是全等图形。下面,让我们一起通过图形运动的方式来认识全等三角形。
一、在图形运动中感受全等三角形
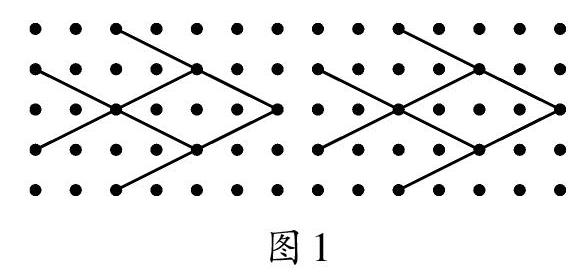
问题1:我们观察图1、图2、图3中的两个全等图形,想一想,怎样改变其中一个图形的位置,使其与另一个图形完全重合?你能按照同样的方法,在这3个图中分别画出第3个、第4个图形吗?(苏科版数学八年级上册第7页。)
通过观察,我们发现,在图1中可以平移其中一个图形得到另一个图形,在图2中可以把其中一个图形翻折得到另一个图形,在图3中可以把其中一个图形旋转得到另一个图形。按照同样的运动方式,我们可以分别画出第3个、第4个图形。
上述过程中,我们经历了观察、比较、思考、画图等活动,体会到图形运动的本质是图形的形状、大小不变,只是图形的位置发生变化。因此,我们可以用动态的、直观的方法认识全等三角形。
二、在图形运动中识别全等三角形的对应边、对应角
两个能完全重合的三角形叫作全等三角形,互相重合的顶点叫作对应顶点,互相重合的边叫作对应边,互相重合的角叫作对应角。表示两个三角形全等时,通常要把对应顶点的字母写在对应的位置上,这样方便找出全等三角形的对应边与对应角。那么,怎样正确地找出全等三角形的对应元素呢?
问题2:图4、图5、图6中的两个三角形是全等三角形,请你找出它们的对应顶点、对应边、对应角。
这3个图形中的两个三角形是全等三角形,说明它们能分别完全重合。我们可以用一张透明纸覆盖在其中一个三角形上,用笔描出这个三角形,然后移动这张透明纸,尝试与另一个三角形重合。在操作活动中,我们发现,图4中,平移△ABC可以与△DEF重合,点A与点D、点B与点E、点C与点F分别重合,这样就找到了它们的对应顶点,接下来就找出了对应边、对应角。类似地,图5中,将△ABC沿BC所在直线翻折,可以与△DBC重合;图6中,将△ABC绕点C旋转180°,可以与△DEC重合。
下面,请同学们用上述方法尝试解决问题3。
问题3:图7、图8、图9分别是两个全等三角形的组合图形,想一想,怎样改变其中一个图形的位置,使其可以与另一个图形完全重合?请你找出各对全等三角形的对应顶点、对应边、对应角。
三、在图形运动中发现复杂图形中的全等三角形
在本章的学习中,我们要认识全等三角形及其性质,学习两个三角形全等的条件,学会利用全等三角形探索图形的性质,其中,识别并证明三角形全等是关键。
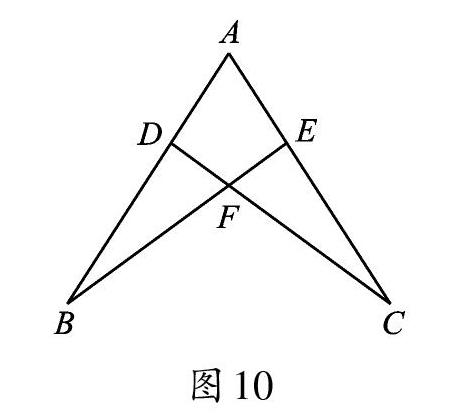
问题4:已知,如图10,点D、E分别在AB、AC上,AB=AC,∠B=∠C,你能证明AD=AE吗?
这个问题中,我们也可以用一张透明纸覆盖在图10上,画出△ABE,尝试与△ACD重合。操作中不难发现,先将△ABE绕点A顺时针旋转,旋转角为∠A,使AE落在AD所在直线上,再沿AD所在直线翻折就能与△ACD重合。更简单的方法是,将△ABE沿AF所在直线翻折与△ACD重合。这样,我们用图形运动的方法找到了全等三角形,接下来思考如何证明△ABE≌△ACD。
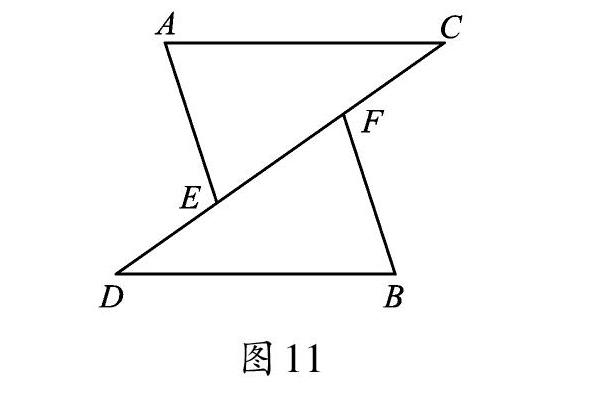
问题5:已知,如图11,点E、F在CD上,DE=CF,AC=DB,且AC∥BD,你发现AE与BF有什么关系?证明你的发现。
观察图形,从直观来看,将△ACE沿EC方向平移,使点E与点F重合,再将△ACE绕点F旋转180°,就可以与△BDF重合,或者将△ACE绕点EF中点旋转180°,就可以与△BDF重合。这样的图形运动给我们提供了思路,通過证明△ACE≌△BDF,从而发现AE=BF,AE∥BF。请同学们自己写出证明过程。
上述两个问题中,我们都是先观察图形,用图形运动的方法先识别两个全等三角形,再根据三角形全等的条件进行证明。接下来,请同学们自己解决以下问题:
问题6:如图12,已知AB=AD,∠1=∠2,∠3=∠4。请找出图中的全等三角形并进行证明。
问题7:如图13,已知∠DAB=∠EAC=60°,AB=AD,AC=AE,BE、CD相交于点O,AB、CD相交于点P,AC、BE相交于点F。你能求出∠DOE的大小吗?
问题8:如图14,已知点C、D在BE上,BC=ED,∠1=∠2,∠3=∠4。图中有哪些全等三角形?请分别加以证明。
图形的平移、翻折、旋转给了我们对全等三角形的初步的、动态的、本质的认识,使我们对全等三角形有了更深刻的感悟。借助图形的运动,我们探索并发现了许多图形的性质。当然,确认一个图形的性质,通常需要运用推理的方法,有时也可以运用图形运动的方法,请同学们在今后的学习中进一步体会。
(作者单位:江苏省盐城市毓龙路实验学校)

