基于BP神经网络的地下水位变幅预测模型
张 蔷
(长治市水文水资源勘测站,山西 长治 046000)
随着水资源供需矛盾的日益突显,部分地区地下水超采引起了地面沉降、岩溶塌陷、地下水体污染等一系列生态地质问题。随着国家最严格水资源管理制度的不断推进实施,水利管理单位需要定量考核用水总量,实施用水单位取水总量控制。因此,有必要依据当地地下水开发利用现状及经济发展用水需求,建立地下水位预测模型,可以定量进行指标控制性管理。
伴随计算机技术的快速发展,神经网络也逐渐被引进到地下水位预测中,从而替代了传统方法[1]。在众多的神经网络模型中,BP神经网络凭借其成熟的预测方法而被广泛采用[2]。BP神经网络模型能够更准确的反映地下水系统的非线性关系,其稳定性较好,精度较高[3]。目前,采用BP神经网络建立地下水水位预报模型成为了主流方法。本文选用BP神经网络模型,建立地下水水位变幅预测模型,模型精度较高,从而达到预测地下水位的目的。
1 长治盆地概况
长治盆地位于山西省东南部,太行山西麓,北与文王山毗连,东与太行山接壤,西与太岳山为邻,南与羊头山搭界,盆地中北部为潞州区,东北部为潞城区,南部为上党区,西南部为长子县,西北部为屯留区,面积为1169km2。长治盆地属季风气候区,多年平均降水量为574.7mm,平均蒸发量为1028.2mm。属海河流域漳卫南运河水系,浊漳河南源是盆地的主要河流,支流主要有绛河、岚水河、陶清河、石子河、碧头河。
长治盆地由黄土丘陵和低山组成,海拔在883.3~981.0m之间,该盆地为新生界早期形成的断陷盆地,广泛分布着第四系的松散堆积物,其厚度由西北向东南逐渐增大,总厚度0~330m,富水性强。新生界松散堆积物的孔隙水主要靠大气降水补给,又接受基岩裂隙水的补给,此外水库、河流及农田灌溉对地下水也有一定的补给作用。
根据多年的地下水动态监测资料以及用水调查统计资料显示,盆地浅层地下水资源开采量逐年增加。供水对象为农业灌溉、农村人畜饮水以及部分工业供水。依据地下水开发利用程度评判指标,长治盆地属于地下水采补平衡区。
随着供水需求得不断增加,集中开采导致部分地区地下水水位下降,引发了以采煤为中心的孔隙含水层被疏干,水井枯竭、水质变差等一系列问题。
2 地下水位影响因子分析
地下水位影响因素较为复杂,收集长治盆地2018-2020年降水量、补给量、浅层地下水水位、实际开采量等资料,并进行分析,降雨量和开采量作为影响长治盆地浅层地下水水位的主要气候因子。长治盆地内代表雨量站共5个,分别为南呈、五里后、西河北、漳泽水库、长子雨量站,采用泰森多边形法,得到盆地平均降雨量。长治盆地分为边坡山区、倾斜平原区和冲洪积平原区,各分区代表监测井共6个,分别为东关、东大关、南关、南呈、北关街和黄南监测井,采用算数平均法得到盆地浅层地下水位。本文采用相关系数法进行分析。
相关系数是衡量两个随机变量之间的线性相关程度的指标,其计算公式为:
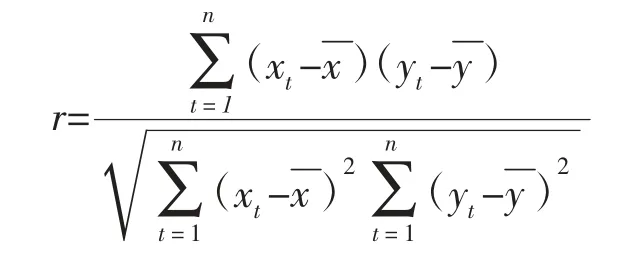
式中:r——相关系数;
xt,yt——分别为x和y的实测值,t为年次;
n——资料年限,t=1,2…n。
采用以上公式,分别计算变量间的相关系数。选定因子为前期降水(其中前期降雨为上一年降雨总量)、本年度降水量、年开采量、上年水位,分别分析这些因子与本年水位以及年水位变幅间的相关性,具体见表1。
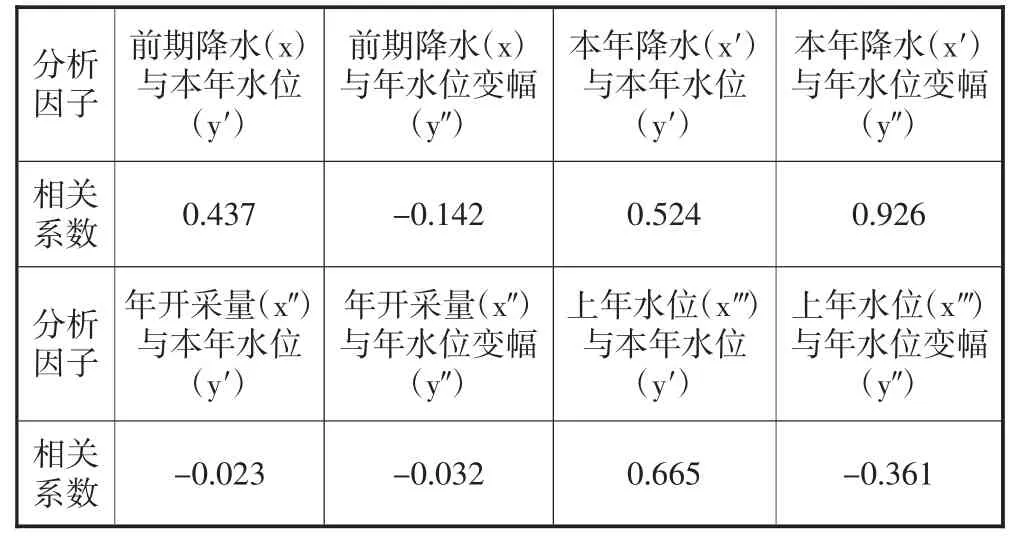
表1 因子间的相关性分析表
通过相关性分析,可以得到本年度降水与水位变幅相关系数为0.926,两者间有较高的相关性。本文选择建立两个模型,其中模型一作为对比模型。
模型一:建立前期降水、本年降水、年开采量、上年水位与本年水位间的关系模型。
模型二:建立前期降水、本年降水、年开采量与年水位变幅的关系模型。
3 模型对比分析
3.1 BP神经网络模型
BP神经网络的结构,主要分为三层输入层、隐含层和输出层。神经网络为自适应的模拟黑箱子模型,输入因子的选择影响着输出结果的精度。通过影响因子分析,选择相关性较好的因子建立模型。本文选择三层网络结构进行模拟。
式中:xi——输入层,即(i=1,2,……,R);
yi——隐含层神经元的输入信号(j=1,2,……,m);
wji——输入层到隐含层的连接权值;
m——隐含层神经元个数;
αj——隐含层神经元的阈值;
wkj——隐含层到输出层的连接权值;
hj——隐含层的输入;
yj——隐含层的输出;
f1——隐含层的激活函数;
k——输出层神经元的个数;
θk——输出层神经元的阈值;
uk——输出层的输入;
f2——隐含层激活函数;
zk——网络输出。
dk——期望输出。
BP神经网络学习算法是基于梯度下降法,通过不断地调整阈值和权值,使神经网络的输出值与所期望的实际值的均方误差达到极小值。
3.2 模型参数的选择
确定BP网络的结构,主要是对输入层、隐含层和输出层的设计,包括网络层数的确定、各层神经元数的确定、各层激活函数的选取、学习率的确定以及最大训练次数的确定。BP神经网络中较为重要的参数设置为:隐含层神经元数和激活函数。
(1)隐含层神经元数是比较难确定的,可能会出现“过拟合”的现象,因此本文参考经验公式确定隐含层神经元数的范围,然后再从该范围中找到最优参数,公式如下:

式中:h——隐含层节点数;
m——输入层节点数;
p——输出层节点数;
α——从0~10之间的任意常数。
(2)激活函数的选择激活函数较为常见的包括:线性函数、阶跃型函数以及S形函数。本文选用正切S型函数,它具有任意阶导数都可以由自身某种形式来表达,并且具有很好的光滑性以及鲁棒性。S型函数公式为:

3.3 模型的建立
BP神经网络是高度非线性动力系统,系统采用S型激活函数,为了有效避开S型函数的饱和区,提高训练的速度,需要对输入的数据进行归一化处理。将输入的数据处理在[0,1]之间,同时也缩小了样本数据不同量纲的差别,一般常用的归一化方法有线性转换函数、对数转换函数以及反余切转换函数。本文选择线性转换函数,其计算公式如下:
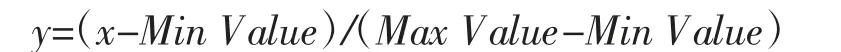
式中:x——样本数据转换前的值;
y——样本数据转换后的值;
MaxValue——输入数据的最大值;
MinValue——输入数据的最小值。
3.4 模型计算
3.4.1 模型一
通过因子分析,可以建立本年水位与上年降水、上年水位、本年水位、年开采量间的关系。前期降水与本年水位的相关系数为0.437,本年降水与本年水位相关系数为0.524,可以看出降水是影响长治盆地浅层地下水的重要因子。采用BP神经网络模型预测本年水位,计算结果详见图2。

图2 三层BP神经网络结构图

图2 实测水位与模拟水位对比图
3.4.2 模型二
通过因子分子,本年降水与年水位变幅相关系数达到0.926,两者之间的相关性更强,两者关系详见图3。因此建立降水与水位变幅间的关系,预报水位变幅值,从而间接得到水位控制指标。

图3 年降水与水位变幅关系图
采用BP神经网络模型预测年水位变幅,计算结果详见图4。
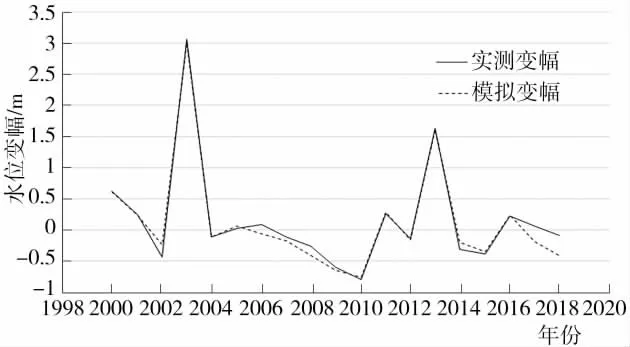
图4 实测水位变幅与模拟水位变幅对比图
3.5 误差分析
为了验证水位变幅预测模型的有效性,采用本年末水位预报模型(模型一)作为参照对比方案。采用确定性系数、误差均方根及误差均值指标,来衡量水位变幅预测模型的预报精度。

式中:N——样本的个数;
yi——实测值;
y^i——模型模拟值。
从表2中可以得到,模型二的确定性系数达到0.98,相对于模型一有了进一步提高,误差均方根和误差均值分别为0.119、0.033均小于模型一,这说明模型二相对于模型一误差降低。因此,相对于之前的水位预报模型,水位变幅预报模型更加稳定,模型精度更高。
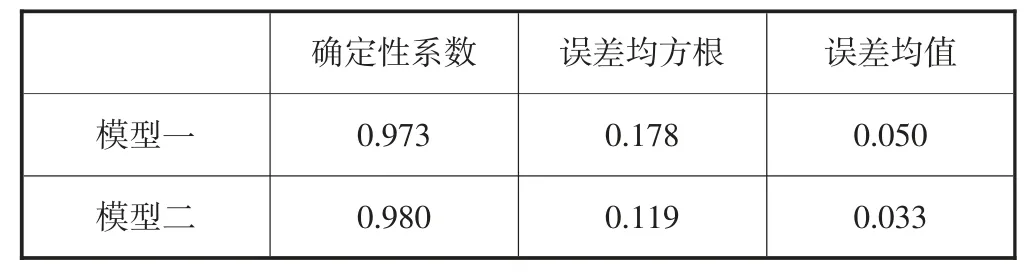
表2 模型误差分析表
4 结论
本文首先对影响浅层地下水因子进行分析,年降雨与年水位变幅的相关系数达到0.926。通过分析降雨时影响浅层地下水数位变幅的重要影响因子,采用BP神经网络方法建立了水位变幅预测模型,相对于之前的水位预测模型,模型计算误差降低,确定性系数达到0.98,模型的精度得到了进一步的提高。因此,在实际应用中,采用水位变幅预测模型能够很好地进行预报,可为控制浅层地下水开采提供技术服务。

