珠江三角洲地区断块运动与应力场特征的数值模拟研究

董纳颖，加依娜·叶尔扎提，刘 洁,2

（1.中山大学地球科学与工程学院，广州 510275；2.南方海洋科学与工程广东省实验室，广东 珠海519082）

0 前言

珠江三角洲地处广东省中部南端、珠江下游，是中国综合实力最强的地区之一。珠江三角洲属于断块型三角洲[1-2]，周边及内部断层纵横交错，基底断裂具有一定的活动性。区域地震危险性研究认为珠江三角洲的地震活动水平较低，但该区域仍属构造活动区，不排除突发性灾害发生的可能[3-4]。三角洲内部的基底面埋深差异较大，显示为断块山与断陷盆地的相间分布，山地、盆地、台地和海域等地区均存在一定的高程差。已有观点推断珠江三角洲的基岩面起伏与断裂活动造成的断块运动相关，然而是否与研究区的莫霍面起伏和应力场的作用方式存在联系，目前还没有更细致的研究。从大湾区城市群的地质安全角度考虑，珠江三角洲区域的地块活动性探讨至关重要。根据珠江三角洲地区的断裂构造建立三维地质模型，探究断裂活动引起的断块运动及应力场特征，对进一步认识珠江三角洲区域的构造演化、大湾区城市的发展建设等具有重要的科学价值和现实意义。

前人采用数值模拟的方法在华南及邻区开展的地学研究多侧重应力场特征的描述或与地震活动的对比分析从而探索研究区的构造演化过程，如：沈立英[5]采用三维有限元数值模拟方法分析了广东及邻区较大范围内的应力场特征及其与地震的关系；闻则刚等[6]采用二维模型模拟计算了广东省范围内的现代地壳构造应力场及其力源；康英等[7]根据震源机制解，采用应力张量反演法确定了广东及其邻区应力主轴的方向并讨论了其构造意义；李红等[8]模拟研究了广州地区4条断裂的现今活动方式及库伦破裂应力年累积速率并与地震活动进行比较；章纯[9]运用数值模拟的方法探讨了台湾地震的发生对华南、华东地区应力场的影响；张亮和栾锡武[10]模拟分析了南海的构造演化过程及控制构造演化的主要因素。

上述研究以二维模型为主，采用的网格模型分辨率较低，材料模型也以线弹性为主，且没有考虑地下不同深度上的温度影响，对珠江三角洲地区的断裂及壳幔结构与基岩面起伏的关系的分析研究涉及很少。因此，本文根据该地区的地球物理数据及活动断裂数据建立三维有限元模型，根据大地热流值建立50 km深度内的温度场，以黏弹塑性本构描述地壳和上地幔的变形特征，采用热-力耦合的三维有限单元方法分析珠江三角洲地区在远场边界条件和先存断裂作用下断块体的差异变形等动态过程，深入研究珠江三角洲地区断块运动与应力场特征。

1 基础资料

1.1 区域地质与断裂

珠江三角洲的地理范围约为112.6°E～114°E，22°N～23.5°N，主要由西江、北江和东江三角洲组成[11]，在构造单元上属于华南褶皱系中粤北、粤东北—粤中拗陷带的粤中拗陷区。珠江三角洲的基底在白垩纪的燕山运动晚期开始成型，并出现了断块山与断陷盆地；准平原化阶段出现在新近纪时期，最终到第四纪晚期才重新开始接受沉积[12]。据历史地震记录来看，珠江三角洲地区没有或很少发生5级以上历史地震[4，13]，地震的活动频率中等，强度较弱。但该区域存在发生强震的构造背景[14]，一旦出现地质安全问题，所造成的损失将是巨大的。因此，城市基底断块（断裂）运动规律及应力场特征的研究仍然十分重要。

本文研究考虑了三角洲内的9条主要断裂（图1）。其中，北东向断裂主要形成于白垩纪的燕山运动晚期，包括五桂山南、北麓断裂、新会—市桥断裂、广州—从化断裂。北西向断裂多处切割北东向断裂，主要形成于渐新世到上新世末的喜马拉雅运动时期，包括西江断裂、白坭—沙湾断裂、化龙—黄阁断裂、南岗—太平断裂，断裂规模相对较小。近东西向断裂主要为瘦狗岭断裂。

图1 研究区主要断裂及基岩等深面图[15]Fig.1 Distribution of main faults and the depth of bedrock in the Pearl River Delta area[15]

1.2 地温场

以珠江三角洲地区的大地热流数据[16-19]为基础，建立研究区地下温度场。热流观测数据的最低值与最高值分别为63.5 mW/m²和83.9 mW/m²，平均值为74.98 mW/m²。

假定地表热流主要源自地幔热流和地壳中放射性元素生热，根据Turcotte和Schubert[19]给出的地温随深度变化公式：

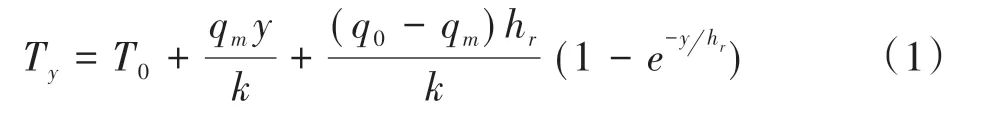
计算地下温度，式（1）中，Ty为地下深度y处的温度；T0为地表温度，取研究区的年平均气温值22.3℃；k为导热系数，取研究区的平均热导率3.34 W/m·K[18]；q0为观测的地表热流值；qm为幔源热流，取全球平均值28 mW/m²；hr为岩石放射性生热层的深度，取研究区地壳的近似厚度30km[21]。莫霍面以下的地温计算公式为：式（2）中，T1为由公式（1）得到的莫霍面处的温度，D1为莫霍面深度，km为地幔岩石热导率，取3.4由此计算得到研究区地下50 km内的地温分布曲线图（图2）。两条实线代表按照地表热流最高和最低值计算的珠江三角洲的地温曲线，虚线为其平均值，对应地下50 km处的温度约为784℃。该值与唐晓音等的研究结果接近[22]。

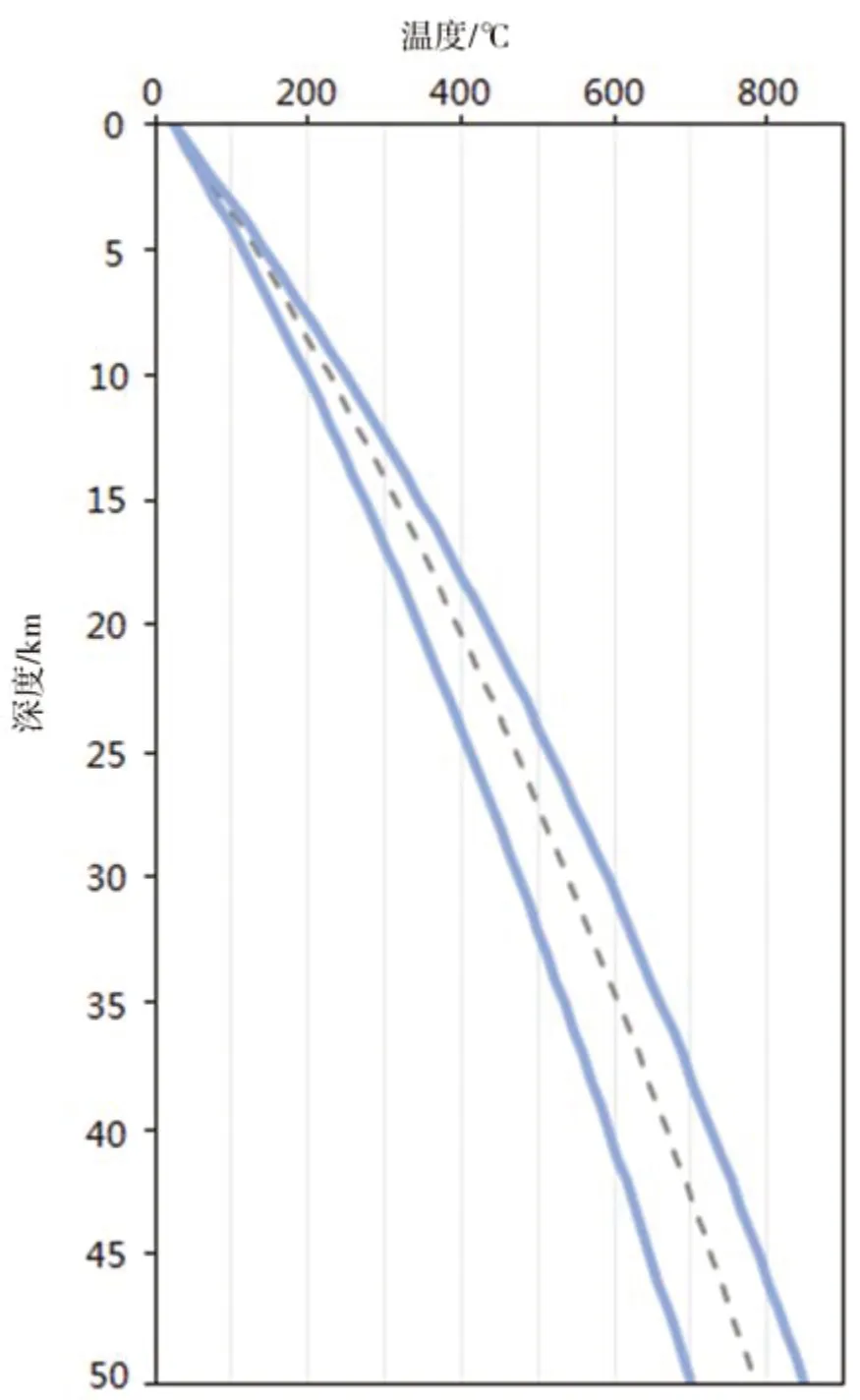
图2 珠江三角洲地下50 km内地温分布曲线Fig.2 Ground temperaturedistribution curve within 50 km underground in the Pearl River Delta

2 三维模型与网格剖分

三维建模的范围较珠江三角洲的实际地理区域（图1）范围大，为112°E～114.5°E，21.5°N～23.8°N（图3a）；模型深度为50 km，包括上、中、下地壳和上地幔顶部四层。采用Geomodeller®软件实施三维建模和网格剖分。

采用分辨率为1°的全球地壳模型Crust1.0数据（http：//igppweb.ucsd.edu/～gabi/crust1.html），确定50 km深度以上的地层划分。根据数据，上、中、下地壳的厚度范围分别约为10～11 km，9～10 km及8～10 km，地幔厚度约为20 km。

在Geomodeller®中添加地层、断层及相关参数并进行建模。根据地表断层观测，瘦狗岭断裂、新会—市桥断裂、五桂山南麓断裂倾向南东，西江断裂和化龙—黄阁断裂倾向北东，白坭—沙湾断裂、南岗—太平断裂倾向南西，五桂山北麓断裂、广州—从化断裂倾向北西，断裂倾角一般介于70°～90°。建模时的断层会自动延伸到模型边界，这与所考虑的区内9条主要断层的实际情况相符。需要注意的是，数值模型中对断层参数的简化会造成局部断层关系与野外观测有差异，但这些局部结构的差异，其影响也是局部的。

三维地质模型建立后，利用Geomodeller®进一步实现网格剖分。三维有限元网格模型如图3b，模型在深度上共划分了15个单元层，节点总数为117936，单元总数为108 000，单元尺度约为3.3 km。Geomodeller®的网格输出数据为vtr格式，不能直接用于Abaqus的模拟计算，需要将其转化为Abaqus格式的节点、单元数据，并定义不同的地层、断层、边界单元以及节点组。数据转化时将莫霍面以下的断层单元修改为该层的普通单元，亦即尽管在建模时断层会自动延伸到上地幔中，但是在模拟时并不考虑地幔中的断层影响。

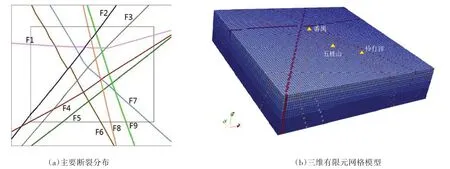
图3 断裂及三维有限元网格模型示意图Fig.3 Schematic diagramof main faultsand the 3Dfinite element mesh model

3 物理模型

3.1 控制方程

本文采用Rosenbaum等[23]分析伸展大陆变形时使用的热-力学耦合的物理模型。本构模型为黏-弹-塑性，综合考虑了浅部塑性破坏、深部蠕变流动及可恢复弹性变形。约定张应力为正，压应力为负。控制方程如下。

（1）质量守恒方程：

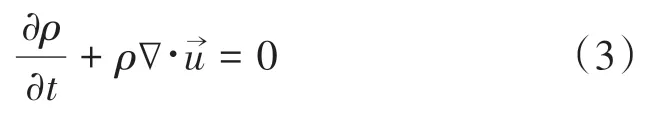
式（3）中，ρ和u→分别是密度和物质速度矢量，t为时间变量。

（2）动量守恒方程

式（4）中，σij为应力张量，为体积力。

（3）能量守恒方程

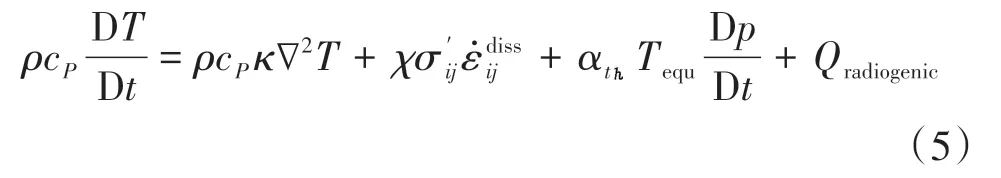
式（5）中，ρ、cP和T分别表示密度、比热和温度，κ为扩散系数，χ为机械功转化为热能的效率为偏应力，是由粘性和脆性应变率导致的耗散蠕变，αt为线性热膨胀系数，Tequ表示绝热体积变化引起的平衡温度变化。

式（5）右端第一项表示热传导；第二项为剪切生热项，本文取χ=1，即假设机械功均转化为热能；第三项为等熵生热，是用于描述如热膨胀与冷却收缩等热弹性效应的弹性反馈项；最后一项为放射生热项。

（4）本构方程

本构方程表达应力和应变之间的关系。总应变率可分为三部分：

式（7）中，E、ν是杨氏模量与泊松比，δij为克罗内克函数，A和n均为材料常数，H、R分别代表活化焓和理想气体常数，R一般取8.314，单位为J·mol-1·k-1，J2为偏应力张量的第二不变量。公式（7）中的第一项为弹性应变率，包括弹性剪切应变率，弹性体积应变率和热膨胀；第二项为塑性应变率；第三项为蠕变应变率，其中参数A、n及H参考高温高压实验获得的石英、长石和橄榄石的相关参数[24-25]。

采用Abaqus®软件实现以上所确定的数值方法。

3.2 材料参数

假设模型各层的力学参数均匀，只考虑层间的参数差异，同时参考Kronenberg等的研究成果[24-25]，设置各地层和断层单元的热-粘弹塑性材料参数（表1）及流变学参数（表2）。

表1 弹塑性及热参数Table 1 Elastic-plastic and thermal parameters

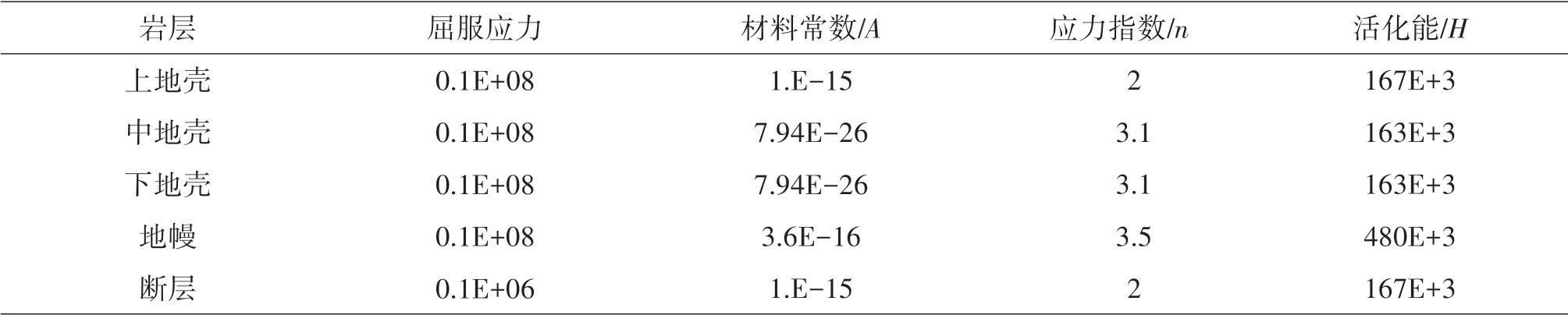
表2 流变学参数Table 2 Rheological parameters

4 计算结果与分析

4.1 边界条件

本文研究区的远场应力条件具有不确定性。地质观测的大量北东向正断层和断陷盆地表明华南地区在中、新生代整体属于伸展构造区，伸展方向为北西-南东[26]；而地震震源机制解给出的现代构造应力场为NWW向主压应力[27]。一种可能的解释是研究区应力场在中生代和新生代早期为NW-SE向伸展，新生代中后期转换为NWW-SEE向挤压[28]。鉴此，本文考虑了4种边界条件，均涉及边界条件的反转。

图4a显示了四种不同边界条件，箭头指示模型侧边界最终受力状态，即：①BC1：东西向位移边界条件，先挤压、后拉张；南北向边界法向约束；②BC2：东西向位移边界条件，先拉张、后挤压；南北向边界法向约束；③BC3：南北向位移边界条件，先挤压、后拉张，东西向边界法向约束；④BC4：南北向位移边界条件，先拉张、后挤压，东西向边界法向约束。所有方案的地表面均为自由面，底部法向约束。最大位移量均设置为10 km，分解到两个对应的边界上分别为5 km。

模拟分析的时间设置为10 Ma，分为四个阶段（图4b）：0～1 Ma为重力沉降阶段，重力作用会引起模型整体沉降且地表面的沉降量最大，逐步增加重力载荷以保证计算的稳定；1～4 Ma为加载阶段，边界位移从0增至10 km；4～7 Ma为卸载阶段，边界位移从10 km恢复到0；7～10 Ma为反向加载阶段，边界位移再次从0增至10 km。尽管边界位移的方向发生了变化，但是速率保持3.3 mm/yr不变。

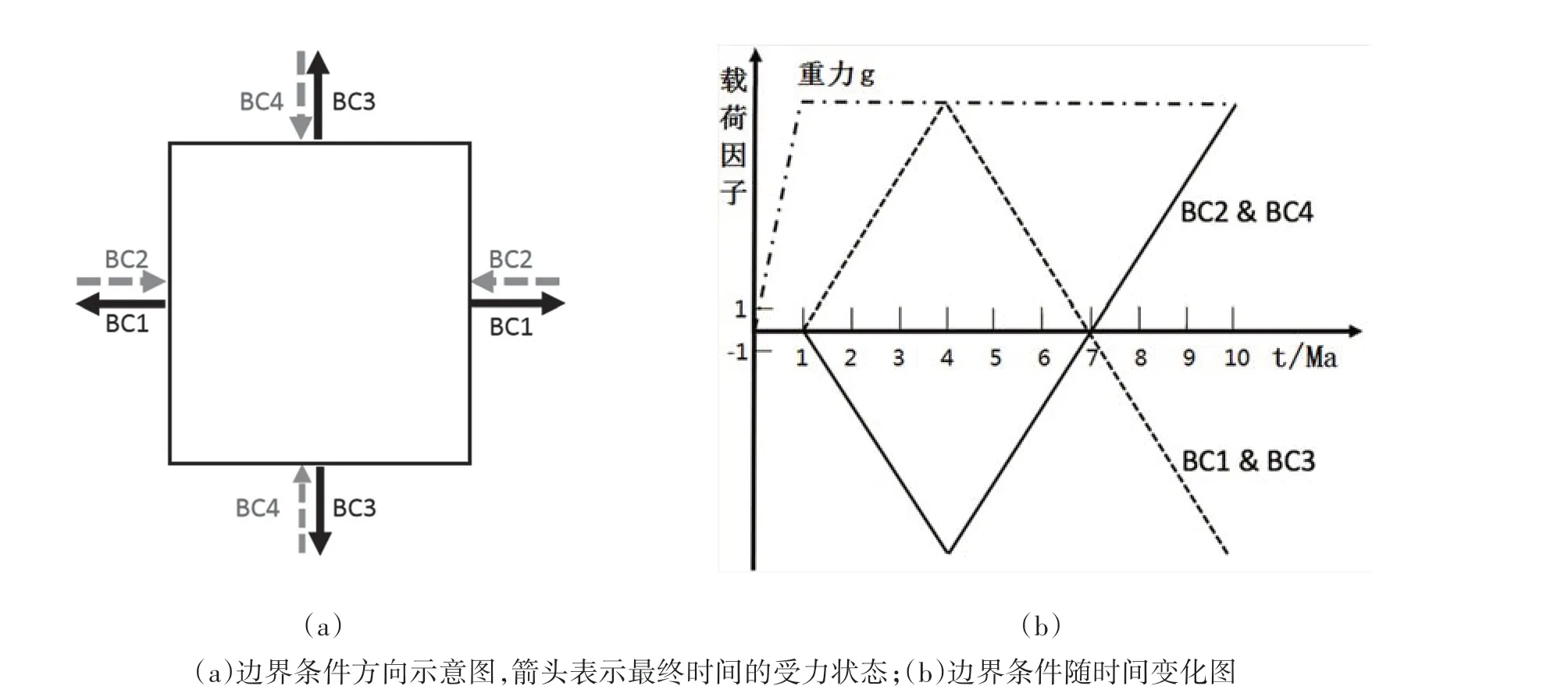
图4 边界条件及随时间变化示意图Fig.4 Schematic diagram of boundary conditions and their changes over time

4.2 对应四种边界条件的结果

图5为BC1情形在10 Ma时的地表位移云图。图5a显示X方向的位移以中轴线为界呈对称分布，东西的最大位移均为5 km左右，与所设边界条件一致。图5b显示Y方向的位移沿不同的断裂带有不同程度的差异，尤其在东西向断裂带的南北侧差异最为明显：断裂以南向南运动，最大位移值约为800 m，断裂以北向北运动，最大位移值约为900 m。图5c显示了垂向位移沿断裂带呈现了一定规律性的分布，断裂附近及交汇处的绿色条带表明断裂部位的垂向位移较四周（蓝色区域）较小。BC2情形也是东西向位移边界条件，地表位移云图的总体分布与BC1情形相似，仅因为位移加载方向随时间变化顺序的不同导致其X方向的位移与图5a相反。

BC3情形为南北向位移边界条件，X方向的位移沿断裂带呈现差异分布，量级约在500～700 m，极值在北东向断层附近；Y方向的位移以南北对称为主；垂向位移的分布依然与图5c相似。BC4情形与BC3情形的差异主要表现在Y方向的位移相反，区域内断块间的差异升降仍然一致。

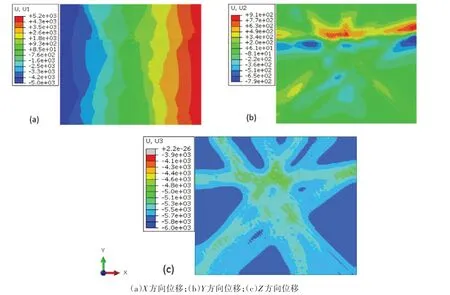
图5 BC1情形计算的t=10 Ma时地表位移云图Fig.5 Cloud map of the surfacedisplacement at t=10 Macalculated in the BC1 case

选取模型中五桂山、番禺台地和伶仃洋地区的地表节点，提取各节点的垂向位移数据并分区块求平均，绘制BC1情形和BC4情形时三个地块的垂向位移随时间变化的曲线（图6）。其中，两种情形下的0～1 Ma间的重力沉降阶段均造成三个区块整体沉降约4 km，后期的构造抬升和沉降应该以这一基础值为参考。图6a为BC1情形下三个地区节点组的平均垂向位移随时间变化的曲线，在1～4 Ma的隆升阶段，五桂山的垂向位移最大，抬升约1.1 km，番禺台地和伶仃洋抬升分别约为1.06 km和0.94 km，五桂山和伶仃洋的最大高差为110 m。在4～10 Ma的下沉阶段，三个地区保持了基本不变的高差整体向下沉降，在模拟结束的10 Ma时，伶仃洋地区的垂向位移最大，下沉约2.85 km，五桂山和番禺台地分别下沉约2.8 km和2.73 km，五桂山和伶仃洋的最大高差为160 m。图6b显示的是BC4情形时同样三个地区节点组的平均垂向位移随时间变化的曲线。尽管位移曲线趋势与图6a不同，但三个典型区块间的相对高程基本一致，10Ma时的地表高程由大到小依次为五桂山、番禺台地和伶仃洋，五桂山和伶仃洋的最大高差为360 m。由此可以推论，模型中这几个位置的垂向位移差异基本不受外部边界作用的影响。

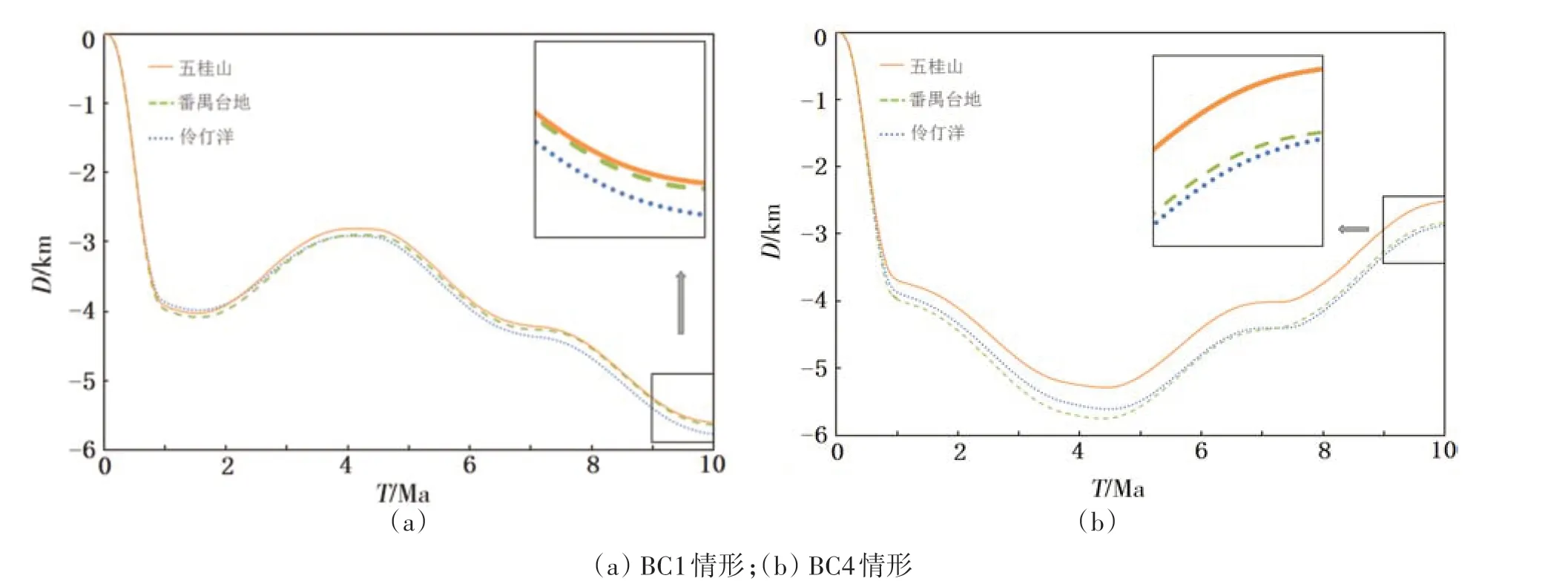
图6 五桂山、番禺台地、伶仃洋区典型单元垂向位移-时间图Fig.6 Vertical displacement-time diagram of typical elements in Wugui Mountain，Panyu platform and the Lingding Bay area

4.3 分别考虑断层和莫霍面起伏影响的断块差异升降

图6所示的五桂山、番禺台地和伶仃洋三个区块的整体垂向运动差异在不同的外边界作用下均相同，意味着造成差异升降的原因在结构内部，即可能由于地层起伏或断层运动造成。为此本研究分别进行了进一步的计算分析：①将计算模型中的莫霍面起伏和断层单元均消除；②将莫霍面起伏消除，仅考虑断层作用的影响（上、中、下地壳间层面本身起伏很小）；③将断层单元消除，仅考虑地层起伏的影响。

显然，将地层起伏和断层单元均消除后，网格模型完全均匀，由此计算的三个地块节点的平均垂向位移起伏完全一致。分别仅考虑断层影响和地层起伏影响的垂向位移随时间的变化见图7。图7a显示当模型中仅有断层影响、无地层起伏、边界条件为BC1情形时，在1～4 Ma的挤压阶段，五桂山、番禺台地和伶仃洋的垂向位移抬升值分别约为1.13 km、1.02 km和1.11 km，在随后的拉伸阶段，五桂山、番禺台地和伶仃洋三个地区的下沉值分别约为2.75 km、2.69 km和2.78 km，在10 Ma时三个区块的地表高程由大到小依次为五桂山、番禺台地和伶仃洋，五桂山和伶仃洋的最大高差为70 m。图7b显示当模型中仅有地层起伏、没有断层影响时，相同BC1边界条件下，在1～4 Ma的挤压阶段，五桂山、番禺台地和伶仃洋的垂向位移抬升值分别约为0.97 km、0.99 km和0.84 km。在随后的拉伸阶段，三个地区保持了与图7a基本不变的高差整体下沉，在10 Ma时，三个区块地表高程的相对位置也与前者相一致，五桂山和伶仃洋的最大高差为160 m。对比图6和图7中三个区块的升降差异可知，莫霍面起伏和断层运动都会影响珠江三角洲断块的差异升降，莫霍面起伏对断块差异升降的影响可能略强于模拟所考虑的断层运动的影响。

图7 五桂山、番禺台地、伶仃洋区典型单元垂向位移-时间图Fig.7 Vertical displacement-time diagramof typical elements in Wugui Mountain，Panyu platformand the Lingding Bay area

4.4 应力场特征

模拟计算结果也给出了不同边界条件下的应力场特征。图8为BC1情形在10 Ma时的应力场方向图。图8a为6 km深度上的主应力场方向分布图。空白区表示应力值较低，圈出的高应力区与图5c所示的高地形区相一致。图中可以看出，应力场方向大多与坐标轴平行，但是断层及邻近单元的应力方向发生了偏转。图8b为15 km深度上的水平最大主应力方向分布图。在近东西向伸展作用的条件下，最大水平主压应力方向为近南北向。同样，断层附近应力场的方向偏转明显，断层交汇区出现压应力高值。图8c展示了在XZ剖面上的主应力方向，箭头大小表示应力值的相对大小，表明应力场随深度明显增加，是重力作用导致的垂向应力占主导地位的应力场的基本特征。图8d为模型南边界附近XZ剖面的Mises应力云图，断层单元均显示代表最低应力值的蓝色，而断层相邻单元的应力值明显高于同一层的普通单元，显示断层活动导致周围应力集中。

图8 BC1在t=10 Ma时应力场计算结果图Fig.8 Calculated results of stress field at t=10 Ma in the BC1 case

其它不同边界条件下的模拟计算结果仅造成最大水平主应力方向的不同，东西向伸展和南北向压缩均使得最大水平主应力为南北向；反之，南北向伸张和东西向压缩使得最大水平主应力为东西向。但是，以所施加的边界条件的强度，垂向应力总是最大值，水平方向两个主应力值较接近，量值大约为垂向应力值的80%。需要补充说明的是，本文不以拟合水平最大主应力方向为目标。上述计算结果的结论对于不同方向水平外边界载荷均成立。

5 结论

本文建立了珠江三角洲地区的三维地质模型，三角洲区域内断裂的影响得以充分考虑；采用热-力学耦合的黏弹塑性材料有限单元方法研究了珠江三角洲地区的断块活动特征及应力场特征。模拟研究结果表明：

（1）珠江三角洲地区的断裂结构控制了区域内的差异升降，模型整体受压时，番禺台地和五桂山地区的抬升较周边地区大，且五桂山的抬升量更大，伶仃洋地区的抬升量最小；在模型伸展时，沉降量的由大到小依次为伶仃洋地区、番禺台地和五桂山地区。这一差异升降规律给出了当前珠江三角洲地区基岩埋深的合理解释。同时，壳幔结构也对研究区的差异升降存在影响。

（2）应力场的最大主压应力表现为重力占主导地位的垂直方向，水平方向应力场受边界条件控制，东西向拉张时，最大水平压应力方向为近南北向；而东西向受压或南北向拉张时，最大水平压应力方向为近东西向。水平方向两个主应力值差异较小。

（3）应力场方向在断层附近因为断层相互运动而明显偏移，例如总体呈南北向的水平主应力甚至可以偏转到东西方向上；而且应力场量值也在断层交汇区出现极大值。

致谢：感谢张小双及陈震为计算参数和模型提供的帮助。感谢“珠江三角洲基底断裂探查与研究项目”（2017201）提供的数据支持。