基于ITD的强震动加速度记录数据处理方法
徐玉聪
(长江三峡勘测研究院有限公司(武汉),武汉 430074)
0 引言
强震动监测是震害评估的重要监测手段[1],高质量的强震动监测记录经过数据处理计算后得到的峰值、持时、频谱和反应谱特征,对于分析研究地震震源机制、建筑物结构响应、评估场地周边灾害具有重要意义[2]。但是强震记录数据由于受到数据记录过程中仪器偏移或者背景噪声等影响,原始记录数据会产生明显基线偏移,这些误差的引入对加速度波形的形态影响并不大,但是对加速度积分之后获得的速度、位移波形和各种反应谱会产生很大的影响[3-4]。因此为了减小由于初始加速度值不为零而产生的误差,有必要在加速度积分得到速度、位移时程之前,对加速度时程进行专门的零线调整[5]。国内外学者对于强震记录的基线校正方法进行了大量研究,各种基线校正处理方法主要集中在滤波法、WiLson校正法[6]、迭代法、分段积分法(Iwan)、经验模态分解(EMD[7-8]等,但是上述方法都存在缺点,例如:滤波法处理结果会影响信号的准确性,、WiLson校正法在基线斜率较大时基本没有校正效果,另外几种处理方法存在依赖于经验判断、计算耗时长、无明确物理意义等缺点。而强震加速度记录作为一种非线性、非平稳的随机信号,需要依赖于信号自身特点进行分析计算,选取合适的处理方法对于快速准确的获得校正加速度十分必要。本征时间尺度分解法(intrinsictime-scale decomposition,ITD)方法[9]能够自适应地将一个复杂信号分解为若干个相互独立的瞬时频率并具有物理意义的合理旋转(properrotation,PR)分量和一个趋势项之和[10],分解过程具有自适应、简单、高效的特点,目前在医学信号分析、机械故障诊断等领域得到了广泛应用。
本文基于本征时间尺度分解ITD算法,首先对比了采用二次拟合法和EMD(TheEmpirical Mode Decomposition)[11]算法的人工合成地震波的数据处理结果,进而对台湾集集地震[12]和某强震动台阵实测未校正加速度进行处理,并采用带通滤波方法进行进一步滤波处理和变换获得校正后的加速度、傅里叶频谱、反应谱,最后通过梯形数值积分计算得到速度和位移,对比分析了经验模态分解(EMD)算法基于上述处理过程和采用强震数据分析软件的计算结果,验证了本文提出的基于ITD基线校正的强震动数据处理方法是稳定、可靠的,可以作为实时、快速的处理强震动加速度记录的一种有效方法。
1 理论和方法
1.1 本征时间尺度分解法算法(ITD)
设Xt为待处理离散信号,并将L定义为基线提取算子,定义Xt=LXt+(1-L)Xt=Lt+Ht,则离散信号的均值曲线表示为LXt,简单记录为Lt,将Ht=(1-L)Xt定义为合理旋转分量(PR),ITD算法具体分解流程如下:
(1)确定信号Xt(t≥0)的极值点Xk及对应的时刻τk(k=1,2,3,…,N,N为所有极值点的个数),简单起见定义τk=0。另假设Lt和Ht定义在区间(0,τk),Xt满足区间范围t∈(0,τk+2)。然后定义信号的分段线性基线提取因子L在t∈(τk,τk+1)范围内为:
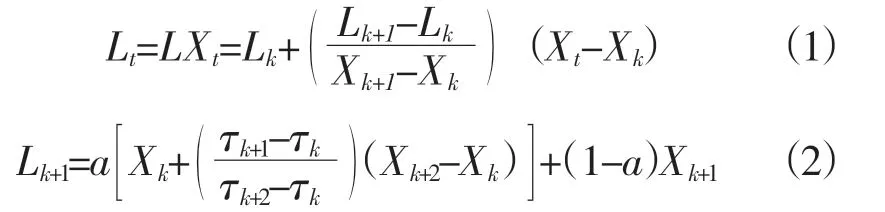
其中t∈(τk,τk+1);a为控制提取固有旋转分量幅度的增益控制参数,0<α<1,通常取α=0.5。
(2)定义合理旋转分量提取因子H,利用计算得到的基线分量Lt可得PR分量Ht为:

(3)将Lt作为下一次分解的输入信号,采用上述步骤进行再次分解,直至最终基线分量单调,则分解过程终止。
(4)通过多次ITD分解,待处理离散信号分解为若干合理旋转分量(PR)和一个单调趋势项之和,最终分解结果可以表示为:

其中HLkXt为第k+1阶的合理旋转分量,LPXt为单调趋势项或最低频率基线。
从上述算法分析,ITD方法中基线的定义是基于信号的线性变换避开了EMD中使用两次三次样条拟合,因此可以减少计算时间,降低拟合之后的误差,所以ITD方法适合在线实时的处理数据。
1.2 基于ITD的强震动加速度数据处理流程
将原始加速度记录通过本征时间尺度分解法算法(ITD)分解后,从原始加速度记录中去除分解后的趋势项,然后通过设计的带通滤波器即可得到校正后的加速度记录,然后通过梯形积分法积分得到速度和位移结果,通过统计分析可以得到最大加速度(PGA)、速度(PGV)和位移(PGD),进一步将校正后的加速度进行变换可以得到傅里叶谱和反应谱等信息,该处理方法具有简单、高效的特点,具体数据处理流程如图1所示。
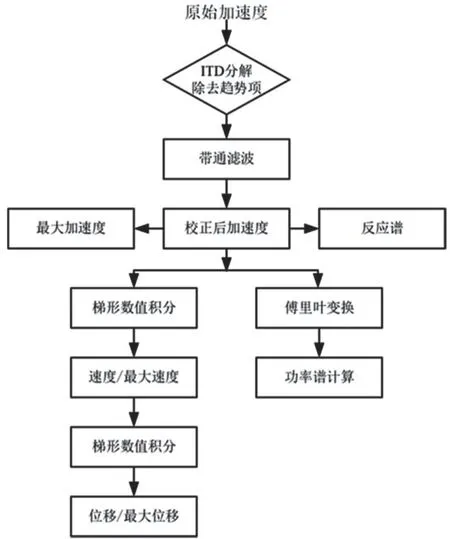
图1 基于ITD的强震动数据处理流程Fig.1 The strong vibration data processing flow based on ITD method
2 人工合成地震波处理分析
为了比较ITD算法、二次拟合法和EMD算法对合成地震波数据的处理效果,选取了1979年美国Imperial Valley地震的一条强震动记录,通过人工合成和加入随机噪声得到合成记录,如图2所示,其中人工合成地震波的采样间隔0.01 s,时间长度40 s,加入3%的随机噪声。

图2 原始地波及合成地震波Fig.2 The original and synthetic seismic waves
图3a、3b为二次拟合法、EMD算法、ITD算法对图2b所示人工合成地震波处理后计算得到的加速度和位移记录。对比速度计算结果,ITD方法、二次拟合法和EMD算法,速度曲线基本一致,EMD方法仅在波形初始阶段有略微波动,说明三种方法对于加速度计算都是有效的;图3b为ITD算法、二次拟合法和EMD算法对位移的计算结果对比,其中ITD算法、二次拟合法计算结果波形基本一致、局部存在差异,而EMD算法在的位移极大值处偏大或者偏小,并且和上述两种方法计算结果的局部波形形态差异较大。
分析图3c为采用三种方法对合成地震波处理后得到的FFT频谱,在数据处理过程中采用了带通通滤波,所以在0.5~30 Hz的有效频段范围内,三种方法计算结果基本一致,说明了采用不同方法进行基线校正过程对于傅里叶频谱计算结果影响不大。
三种方法计算得到的位移反应谱如图3d所示,位移反应谱差异集中在周期2~4 s之间;其中在2~3.5 s之间,ITD算法和二次拟算法形态基本一致,仅在数值有差异,而EMD方法和另外两种方法计算结果相比形态差异较大;ITD算法、二次拟合法形态差异主要原因是随机噪声的引入,而EMD方法计算结果差异还由于算法本身缺陷而引起。
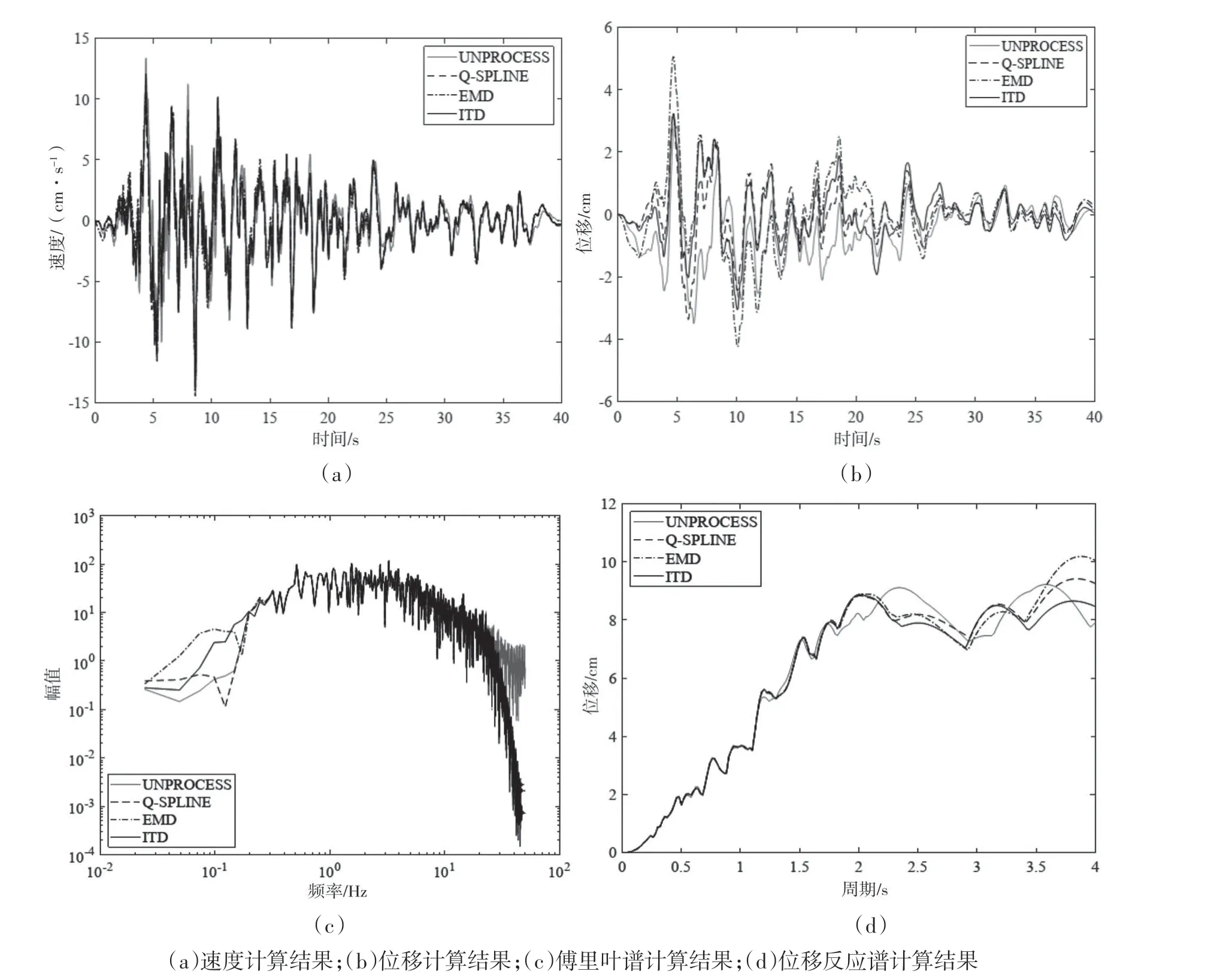
图3 不同方法合成地震波的计算结果对比Fig.3 The comparison of calculation results of seismic wave synthesized by different methods
通过对人工合成地震波计算结果对比分析,ITD算法和二次拟合法处理结果基本一致,EMD方法总体计算效果不稳定。
3 实测资料处理对比分析
由于ITD算法和EMD算法均属于模态分解方法,而目前强震分析软件主要采用二次拟合法对原始加速度记录进行基线校正处理。为了验证ITD算法对实际强震动记录的处理效果,将对比EMD算法,另外将基于二次拟合法的强震分析软件作为参照,对台湾集集地震加速度记录和某强震监测台阵实测资料进行处理分析。
采用ITD分解算法和EMD分解算法,基于章节1.2提出的强震动加速度数据处理流程,选取了集集地震中TCU079(台站代码B079)、TCU116(台站代码B116)、TCU122(台站代码B122)3个强震动监测站和某强震动监测台阵S1、S2、S3测点记录到的三分向强震加速度记录进行计算处理,并采用强震处理软件(SPA)进行参照计算,得到了图4所示的不同方式处理后的PGA、PGV、PGD计算结果。

图4 强震动加速度处理结果Fig.4 The processing results of strong vibration acceleration
从采用三种方式计算得到的图4a、4d所示PGA结果来看,ITD分解算法、EMD分解算法和强震软件处理结果误差不大;但是从图4所示PGV、PGD计算结果分析,ITD分解算法和强震软件处理结果相近,说明ITD算法是稳定、可靠的。但是EMD算法处理结果另外两种方式差别较大,特别是最大位移结果基本上反映不出来真实的计算结果,这与EMD算法对人工合成数据处理后存在波动是对应的,这种微小的误差波动对在处理实际强震记录数据时经过两次积分获得位移将产生巨大误差,基本无法识别真实的结果。
图5是图4中ITD分解算法、EMD分解算法和强震软件处对强震动监测台阵S3测点垂直向原始加速度记录的计算结果,数据时长120 s,采样频率100 Hz,进行带通滤波,图5a~5d分别是计算得到的速度、位移、FFT频谱和反应谱曲线,ITD分解算法和软件计算结果曲线形态基本一致;EMD算法计算得到的位移曲线和FFT谱曲线对主要强震记录之外的数据形态进行了放大,导致波形产生大幅度的跳变,导致计算结果严重失真;EMD计算得到的反应谱在固有周期2.5~4.0 s也产生了波动,主要还是由于加速度记录处理阶段的误差引起。
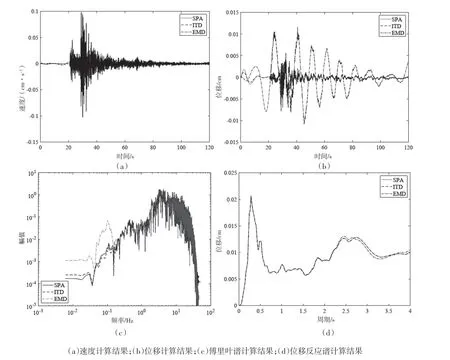
图5 ITD分解算法、EMD分解算法和强震软件处理结果Fig.5 The calculation results by the methods of the ITD,the EMD and the strong earthquake analysis software
从ITD分解算法、EMD分解算法和强震软件对集集地震加速度记录和某强震监测台阵实测资料处理结果对比分析可知,ITD分解算法可以而有效的对强震动记录进行基线校正,并且通过后续的带通滤波、梯形数值积分计算得到的速度、位移和FFT频谱、位移反应谱与强震软件的处理结果对比误差很小,所以ITD分解算法对实际的强震动记录处理计算都是有效的。
4 结语
通过对人工合成地震波数据的对比计算分析,相比于EMD等方法,ITD分解算法能够自适应的分解出数据中的趋势项,并且不依赖于先验因子,该算法稳定、适用性强;对实际强震加速度记录分析表明,ITD分解算法可以有效的在对强震动记录数据处理过程中进行基线校正,并且通过后续的带通滤波、梯形数值积分计算得到的速度、位移基本可以达到强震分析软件的效果,所以ITD分解算法对原始加速度基线校正以及后续速度、位移等的计算处理都是适用的。所以本文提出的基于ITD分解算法的强震加速度数据处理方法能够稳定、可靠的处理的强震动记录。

