浅水区串联航行体超空泡流动特性研究
周 栋,施红辉,周东辉,张程伟,王焯锴
(浙江理工大学 机械与自动控制学院,浙江 杭州 310018)
航行体在水下高速运动时形成的超空泡显著降低了航行体所受的水的黏性阻力,使航行体能够获得90%以上的减阻量,航行体的速度因此得到极大的提升[1]。因此,超空泡在国防军事方面(水下兵器领域)有着重要的应用,一直是高速水动力学领域研究的热点之一。
目前,对于水下及近自由面下的超空泡流动研究已经有了很多的结果。NOURI等[2]采用边界元法对超空泡势流进行了数值研究,提出了一种求解二维对称流动空腔边界的迭代算法,可以与边界元法或其他数值方法相结合来预测超空泡流动的特性。易文俊等[3]研究了不同空化器结构以及不同空化数下的水下射弹超空泡的形态特性。胡雨博等[4]对76 mm直径高速射弹进行了数值模拟,分析了不同速度下超空泡的演化规律以及阻力特性。施红辉等开展了高速射弹水平入水实验并分析了水深和弹体长径比对超空泡弹体阻力系数及空泡形状的影响[5];模拟了不同表面凹槽数的水下航行体的超空泡流场,得出凹槽数增加会导致超空泡外形轮廓变小[6];研究了水平运动超空泡在近自由面区域的水动力学特性,分析得出深水区自然超空泡的外部轮廓近似一个椭圆,而浅水区自然超空泡的外部轮廓具有非对称性[7]。王一伟等针对水下航行体云状空化问题,开展了实验和相关数值模拟,并通过数值模拟结果验证了预测公式的有效性[8];还进一步研究了近自由面轴对称弹丸的云状空化现象[9]。徐畅等[10]针对近自由面的轴对称弹丸的超空泡流动进行了实验研究,并基于Volume of Fluid(VOF)和Large Eddy Simulation方法进行数值计算,得到了空腔和水层的非定常特性。
目前,对于浅水区超空泡的流动研究主要集中在单个航行体,关于浅水区串联航行体的超空泡流动研究还未见公开报道。在浅水区利用超空泡射弹或者超空泡鱼雷饱和攻击时,必然涉及到超空泡武器的串联运动,此时就需要考虑2个甚至多个超空泡之间的相互作用、超空泡与自由面的相互作用等问题。串联超空泡航行体周围流场相互影响、干扰,引起航行体间流场的变化,与单独航行体的超空泡有很大的区别[11]。串联航行体超空泡的流动特性既包含单个航行体超空泡的流动特性,又具备自身的复杂性。因此,有必要研究浅水区串联航行体的超空泡演化规律,这在理论研究和工程应用上都具有重要意义。本文基于VOF多相流模型,建立了浅水区串联航行体的数值模型,利用FLUNET计算流体力学仿真软件数值模拟了浅水区串联航行体的超空泡流场,研究了水深和航行体间距对超空泡流动的影响。
1 控制方程和数值方法
1.1 计算模型
航行体模型来源于文献[5]的实验射弹模型,该模型其质量约4.62 g,材料为镁铝合金;航行体为圆柱体,其长度Ln=60 mm,直径Dn=6 mm,长径比为10,如图1所示。

图1 航行体模型


图2 串联航行体各项参数定义
1.2 控制方程
浅水区超空泡的流动涉及到气、汽、液三相之间的相互作用,具有其复杂性,所以本文数值计算基于VOF多相流模型,包含空气、水、水蒸气三相。
连续性方程和动量方程[12]分别为
(1)
(2)
式中:ρ为混合物密度;t为时间;ui,uj分别为i和j方向的速度分量;xi为i方向的坐标分量;μ为混合物动力黏度;p为流场的压力;SM为附加的源项。
ρ,μ的表达式分别
ρ=αvρv+αgρg+αlρl
(3)
μ=αvμv+αgμg+αlμl
(4)
式中:α,ρ,μ分别为体积分数、密度和动力黏度;下标v,g,l分别表示水蒸汽、空气和水。
标准k-ε湍流模型[13]基本形式为

(5)
(6)
式中:k为湍流动能;ε为耗散率;μt为湍流黏性系数;Prk,Prε分别为k和ε的湍流普朗特数;Gk为速度梯度湍流动能;Gb为浮力湍流动能;YM为可压湍流中振荡膨胀对耗散率的贡献;Sk,Sε为附加源项;C1ε,C2ε,C3ε为常数。
Schnerr-Sauer空化模型[14]水蒸气相的体积分数一般形式为
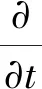
(7)
(8)
(9)
式中:Re为蒸发速率,Rc为冷凝速率,vv为水蒸气相的速度矢量,rB为气核的半径,pv为水的饱和蒸汽压力。
1.3 数值方法
1.3.1 边界条件设置与网格划分
数值模拟的计算模型为位于浅水区的轴向串联航行体,定义相邻两航行体的间距为l;水深为h;计算区域长度为3 000 mm,宽度为1 500 mm,上方为空气,下方为水。边界条件设置如下:上部、下部以及航行体均为无滑移壁面边界条件,左侧为速度进口边界条件,右侧为压力出口边界条件,如图3(a)所示。本文计算区域均采用四面体网格,并对自由面以及航行体周围网格进行加密处理,如图3(b)所示。上述计算模型中压力与速度耦合的求解采用Coupled算法,压力场和空间离散采用PRESTO格式,体积率离散采用Modified HRIC。

图3 边界条件及网格划分
给定航行体速度以及航行体直径可以求得弗劳德数[15]:
(10)
式中:v∞为航行体速度;g为重力加速度;Dn为航行体直径;其中v∞=60 m/s,g=9.8 m/s2,Dn=6 mm,根据公式(10)可得Fr=247.4≫30。故依据重力效应的判断准则,可以不考虑重力因素的影响[11]。
1.3.2 数值方法验证

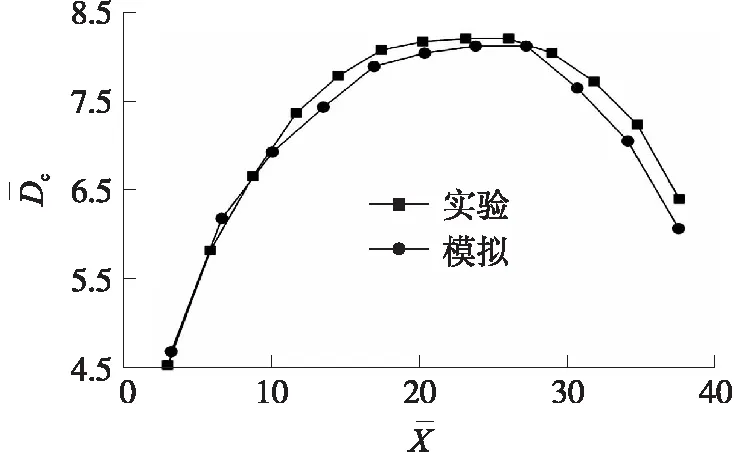
图4 单个航行体实验与模拟对比


图5 不同网格数量下的前航行体无量纲空泡上部轮廓曲线

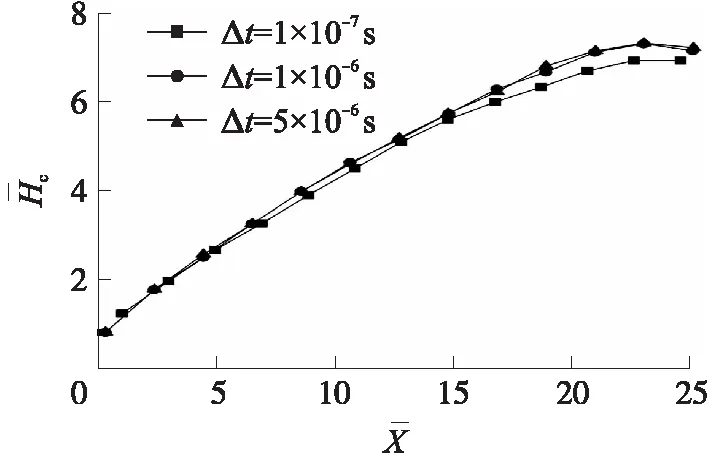
图6 不同时间步长下的前航行体无量纲空泡上部轮廓曲线
2 数值计算结果与分析
2.1 典型工况计算结果
在典型工况中,串联航行体速度为60 m/s,水深为20 mm,航行体间距为120 mm(2Ln),记为工况1。将数值模拟结果经过CFD-Post处理之后得到串联航行体超空泡水相图,如图7所示。

图7 不同时刻串联航行体超空泡水相图

由图8可见:从t=3.6 ms开始,后航行体开始进入前航行体的超空泡流场,与前航行体的超空泡流场发生相互作用;在t=6.6 ms后航行体已经完全进入前航行体产生的超空泡内,最终前航行体产生的超空泡包裹着2个串联航行体在一个空泡内运动;空泡右上部分的水层已经很薄,空泡开始破裂并从超空泡后部卷入空气,超空泡逐渐变大,后航行体产生的空泡逐渐溃散并消失,与施红辉等[5]实验结果一致;在t=12 ms之后,上部空气卷入空泡内部的速度逐渐变慢,并在某一时刻不再卷入;在t=23 ms超空泡充分发展,空泡前后轮廓近乎对称。图9给出了典型时刻t=1.2 ms时前航行体头部前端10 mm附近压力分布曲线,图中以航行体中心线位置为分界点,向上为正,向下为负。

图9 工况1中t=1.2 ms时刻前航行体头部附近压力分布
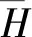

图10 不同时刻无量纲波浪高度
2.2 不同水深的影响
为了探究水深h对串联航行体超空泡流动特性的影响,本文计算了4个水深(h=20 mm,60 mm,200 mm,400 mm)的工况,分别记为工况1(即前文工况1)、工况2、工况3、工况4,除水深不同外,串联航行体速度均为60 m/s,航行体间距为120 mm(2Ln),如表1所示。

表1 不同水深工况汇总
取典型时刻t=1.2 ms,分析不同水深时前航行体(以航行体中心线位置为分界点,向上为正、向下为负)头部前端10 mm附近压力分布。由图11可知:在浅水区空泡上、下压力差异较大,而在深水区空泡上、下压力差异较小,这也是导致浅水区空泡上部轮廓较凸、下部轮廓较为平缓,而深水区上、下空泡轮廓几乎对称的原因。

图11 t=1.2 ms时刻不同水深对前航行体头部附近压力分布
在工况2(h=60 mm)工况中,取典型时刻t=3.6 ms,6.6 ms,8.4 ms,12 ms,水相图如图12所示。由图7、图12可知:工况2(h=60 mm)与工况1(h=20 mm)相比,后航行体开始进入前航行体形成的超空泡时刻基本相同,约在t=3.6 ms时刻。不同的是:约在t=6.6 ms时,工况1(h=20 mm)后部空泡开始破裂并从上方卷入空气;而工况2(h=60 mm)空泡后部不再破裂,没有上方空气卷入,如图13所示。这可能是因为工况2中设置的水深h相对于航行体的直径足够大,此时水深约为10Dn,由此推论:当水深h远大于Dn时,尽管存在自由面的影响,但是水深相对于航行体直径足够大,上方空气不再卷入超空泡内。

图12 工况2(h=60 mm)不同时刻串联航行体水相图

图13 t=6.6 ms时刻工况1和工况2串联航行体水相图
取典型时刻t=21 ms,得到不同水深时串联航行体的最大波浪高度、最大空泡直径、最大空泡长度,如表2所示。由表2可知:最大波浪高度、最大空泡直径在浅水区时较大,而在深水区时较小;最大空泡长度在浅水区时较小,而在深水区时较大。

表2 t=21 ms不同水深时各项参数汇总

(11)
(12)

水深一定的情况下,在航行体高速无推力自由运动过程中,忽略重力和浮力的影响,空化数仅由航行体速度v决定,空化数[17]的表达式为
(13)
式中:p0为标准大气压,其值为101 325 Pa;ρl为水的密度;pc为空泡内部压力,即水的饱和蒸气压,这里取值pc=3 540 Pa;v∞为航行体速度,本文设定v∞=60 m/s。求得空化数σ=0.054。
(14)
不同水深时得到的超空泡无量纲直径与根据Logvinovich半经验公式得到的空泡截面直径进行对比,如图14所示。由图14可知:在浅水区时,4种水深时的最大空泡直径要明显大于Logvinovich半经验公式得到的值,这是由于在浅水区运动的航行体形成的超空泡上下压差较大,表现为上部较凸,下部较为平缓,不再满足独立膨胀原理。而随着水深的增加,空泡上下轮廓趋于对称,无量纲轮廓曲线更加平缓。

图14 t=21 ms时不同水深无量纲空泡截面直径曲线
2.3 航行体间不同间距的影响
为了探究串联航行体间的间距l对串联航行体超空泡流动特性的影响,本文计算了4个间距,120 mm,240 mm,300 mm,480 mm(即l=2Ln,4Ln,5Ln,8Ln)4种工况,分别记为工况1(即前文工况1),工况5,工况6,工况7。除间距不同外,串联航行体速度均为60 m/s,水深均为20 mm,如表3所示。

表3 航行体间不同间距工况汇总
取典型时刻t=6.6 ms,研究串联航行体匀速运动下的超空泡流动特性,如图15所示。由图可知:t=6.6 ms时,随着串联航行体间距的增大,前航行体后部卷入空气增多,后航行体后部卷入空气差异不大;在工况1(l=120 mm)中,后航行体已经完全进入前航行体形成的超空泡中;在工况5(l=240 mm)中,后航行体即将进入前航行体形成的超空泡中;在工况6(l=300 mm)以及工况7(l=480 mm)中,后航行体进入前航行体形成的超空泡仍需要一段时间,后者更甚。由此推论:随着前后航行体间距的增大,后航行体进入前航行体形成的超空泡的时间越迟。

图15 t=6.6 ms串联航行体不同间距水相图
图16为串联航行体超空泡充分发展阶段在典型时刻t=21 ms时的超空泡外形轮廓曲线。

图16 t=21 ms不同间距时无量纲空泡截面直径曲线
由图16可以看出:随着航行体间距的增大,超空泡轮廓变得越加平缓;l<5Ln时,4Ln与2Ln间的差异比8Ln与5Ln间的差异更明显,且8Ln与5Ln的走势比较接近,故可以近似认为5Ln为临界间距;当间距l≥5Ln时,不同间距的串联航行体超空泡轮廓差异不大。
3 结论
①前后串联航行体形成的超空泡流场相互影响,后航行体进入前航行体的超空泡流场后,与前航行体的超空泡流场发生相互作用,最终前航行体产生的超空泡包裹着2个串联航行体在一个空泡内运动;在浅水区,空泡发展到一定时刻,空泡尾部上方的水层已经很薄,空泡开始破裂并从超空泡后部卷入空气,超空泡逐渐变大,后航行体产生的空泡逐渐溃灭并消失。
②在浅水区,空泡上下压力差异较大,而在深水区空泡上下压力差异较小;浅水区下超空泡形状总体表现为上部较凸,下部较为平缓,而随着水深的增加,空泡上下轮廓趋于对称,并且空泡的无量纲轮廓曲线更加平缓。
③随着航行体间距的增大,后航行体进入前航行体形成的超空泡的时间越迟;串联航行体超空泡充分发展阶段,随着航行体间距的增大,超空泡轮廓变得越加平缓,当间距l≥5Ln时,不同间距的串联航行体超空泡轮廓差异不大。

