可分辨空间密集目标群跟踪算法研究

修建娟,董 凯,2,徐从安

(1.海军航空大学,山东 烟台 264000;2.中国电子科学研究院,北京 100041)

飞机、舰船等有动力装置的密集目标群的目标间距相对较大,而且不同目标之间存在相对运动、目标运动状态也有一定差别[1-3],为了避免被跟踪、被拦截,空间目标在飞行中段产生的碎片、释放的诱饵以及其他伴飞目标(假弹头等)构成空间目标群,该目标群具有运动速度快、密集性高、可分性差、目标运动特性非常相近等特点[4-7]。空间密集目标不可分辨情况下可采用群质心跟踪或扩展目标跟踪方法[8-10],其中扩展目标跟踪比较适用于飞机、舰船等有具体形状限制的群跟踪[11-12]。空间目标可分辨情况下的跟踪方法有很多[13-19],其中基于概率数据关联和最近邻等的空间多目标跟踪算法在目标密集性比较高的环境下容易出现关联错误,导致目标频繁出现航迹中断和重复起始等问题,有效跟踪的目标数量低、精度差。在跟踪过程中增加其他有用信息可以提高关联正确率,但这也会增加算法的复杂程度,影响空间目标跟踪的实时性。联合概率数据互联算法(JPDA)能够较好地实现密集多回波下的多目标跟踪,但该算法(包括其改进算法)对弹道导弹群目标这种群成员众多、成员之间方向随机、间距复杂的多目标不能有效地进行跟踪[6]。基于随机有限集的群目标跟踪算法有效回避了多目标跟踪中最难以解决的数据关联问题[20],但该类方法的计算量也普遍偏大,很难保证运动速度非常快的空间群目标跟踪的实时性。

为了有效改善可分辨高速空间目标群早期的跟踪态势,提高目标群的跟踪处理速度和跟踪精度,本文提出了可分辨空间密集目标群跟踪算法,该算法首先通过全局聚类群分割、群关联和群跟踪,解决大量距离靠近、运动特征差异不明显的高速空间目标群早期连续稳定跟踪问题,在此基础上,边跟踪边分群,将群目标跟踪逐渐过渡到多目标跟踪,在群目标跟踪中通过结合空间动力学方程提高群内空间目标的跟踪精度,避免跟踪早期由于重复起始导致的大量短小航迹,提升空间密集目标数据处理能力和跟踪精度,为后续目标运动轨迹预报和可靠拦截等提供数据支持。

1 空间群目标分割

为了更好地掌握可分辨目标群跟踪早期的整体信息,提高目标数据的处理速度,本文首先基于全局聚类对群目标分割问题进行研究,该方法在分割过程中不断以群中心以外的其他数据为中心再次寻找落入群门限内的量测,以有效避免分群时群中心数据位于外围边缘所带来的影响,相关过程具体如下。

设Z(k)表示雷达在k时刻所获得的直角坐标系下的转换量测数据集合:

(1)

式中:mk为k时刻转换测量数据数量,第i个数据表示为zi(k)=(xikyikzik)T。

在量测集合Z(k)中的数据多于一个的情况下按如下步骤进行群分割:

1)设立分群指示,初始时刻第1个群目标的分群指示定义为1,其余为0;

2)以k时刻第1个目标的转换测量数据z1(k)为中心,以d0为阈值建立波门,若

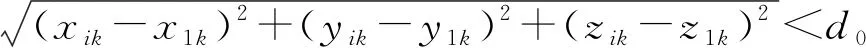
(2)

则判断数据zi(k)和z1(k)属于同一个群,其中阈值d0可结合群目标密集程度、目标类型等进行设置。设置的d0越大,密集目标作为群整体跟踪的时间越长;反之,设置的d0越小,群内目标越快分离出去变为多目标跟踪。

在以d0为门限的分群过程中,根据目标密集程度又可分以下2种情况:

①若k时刻全部数据zi(k)(i≠1)和z1(k)的距离均小于门限d0,则判定该时刻的所有目标测量数据均落在一个群内,计算群中心数据如下:

(3)

式中:(xlk,ylk,zlk)为落入该群内的第l个数据;m1为落入第1个群中的数据数量。

②如果k时刻只有部分数据和z1(k)的距离小于门限d0,则首先由这些数据获得群中心相关信息,同时以该群内其他目标(目标1除外)为中心对落在群门限外的数据进行判断。如果判断有数据和第1个群内其他目标的距离小于群门限,则该数据仍判断属于第1个群,并利用这些数据对群中心数据进行更新。

3)若k时刻所有数据均判断完毕后,仍有数据和第1个群内所有目标的距离均大于群门限,则以这些落在群门限外的数据为中心进行新群的分割。

①如果落在第1个群外的数据多于一个,则第2个群目标的分群指示变为1,重复步骤①、②完成第2个群目标的判断;

②如果落在第1个和第2个群目标外的数据多于1个,则第3个群目标的分群指示变为1,重复步骤1)、2)完成第3个群目标的判断;

③依次类推,直到k时刻的所有测量数据均分群完毕,然后对下一时刻目标测量数据进行分群。

2 空间群目标关联

在完成群分割的基础上,还需解决多群情况下的群关联问题。考虑到弹道目标运动速度很快,传统多目标数据关联方法在密集目标环境下为了保证关联效果处理过程往往比较复杂,实时性很难保证;而简单的数据关联算法实时性提高了,但关联效果往往不尽如人意,数据关联有可能存在“先占先得”问题,即先关联目标(例如目标A)抢占的数据是另外一个目标(目标B)的有效数据,目标B的正确数据被抢占了,它关联上的数据又会影响到其他某个目标,形成连锁反应。密集性较高的空间目标环境下该问题的影响尤其严重,为此本文提出基于双向互选方法解决群关联问题。该方法首先根据空间群目标统计距离构造检验统计量,在此基础上基于最近邻准则由目标在全局范围内选择关联的群数据,当选择的群数据出现归属矛盾时,再根据该矛盾数据对目标进行选择,通过目标与群数据的互相选择确认来提高数据关联的正确率,具体步骤如下:

1)将某时刻获得的群数据分别给予相应的目标编号,这里的群数据是指经过坐标转换后直角坐标系下的转换测量群中心数据。

2)将雷达下一时刻所有的群数据依次和不同目标前一时刻群数据通过波门进行关联,这时又分为以下几种情况:

①若下一时刻所有的群数据全部落在前一时刻的某个(例如第i个)群目标的波门外,则该群目标(第i个)下一时刻数据漏检,赋“0”值。

②若下一时刻有群数据落在前一时刻的某个群目标(例如第i个)的波门内,则取和波门中心距离最近的群数据予以关联,完成群目标1候选数据的关联判断;同理,其他群目标也需和所有群中心数据做关联判断。

③从第2个群目标开始要判断选择的群中心数据和前面几个群目标选择的是否相同。

④如果判断有2个以上群目标选择了相同的群数据,则由该群数据对群目标做选择,并将该数据从群数据集合中去除。

⑤将没有关联冲突(即和唯一群目标关联)的群数据也去除,如果此时群数据集合中仍有未找到归属的数据,则将它们和前面冲突关联中剩余的群目标按步骤2)进行关联判断。

⑥群数据在和所有群目标均完成关联判断后,仍有未找到归属的群数据,则将这些群数据作为新出现群目标给予相应的群目标编号,按步骤2)进行关联判断。

3 基于空间动力学方程约束的群跟踪

3.1 空间动力学方程约束的系统模型

传统跟踪算法中目标状态方程通常建模为

X(k+1)=F(k)X(k)+V(k)

(4)

式中:F(k)为k时刻的状态转移矩阵,X(k)为状态向量,V(k)为零均值的高斯白噪声,其协方差为Q(k)。

考虑到中远程空间目标在中段惯性飞行阶段仅受重力作用[16,21],具有椭圆运动轨迹的特点,为此,从空间目标运动特性出发,利用空间目标动力学方程实时对式(4)给出的状态方程进行修正,建立空间目标动力学方程约束下的状态方程:

X(k+1)=F(k)X(k)+D(k)f(X(k))+V(k)

(5)

式中:f(X(k))为空间动力学方程约束下实时加速度估计[20-21],此处为雷达站东北天(ENU)坐标系下的空间目标加速度,即

(6)

式中:μ为万有引力常数,J2为地球二阶带谐系数,re为地球赤道半径。

(7)

z′(k)=z(k)+re+h

(8)

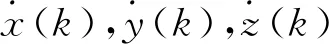
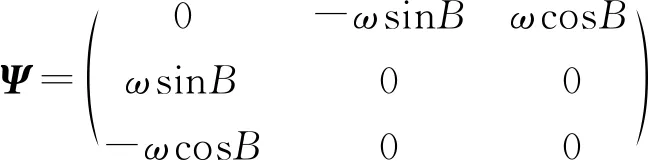
(9)

式中:B为雷达站大地纬度,ω为地球自转角速度。

状态向量和状态转移矩阵分别为

(10)

(11)

式中:O3×3为3×3的全零矩阵;Φ(k)为x,y或z轴数据对应的状态转移矩阵,这里采用Singer模型,即

(12)

式中:T为采样间隔;α为机动时间常数的倒数,即机动频率。系数矩阵为

(13)

空间目标量测方程为

Z(k)=h(X(k))+W(k)

(14)

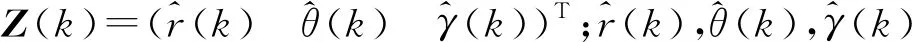
(15)

W(k)为量测噪声序列,且假定其为零均值、协方差为R(k)的白色高斯噪声,且

(16)

3.2 空间动力学方程约束的滤波模型

在式(4)和式(14)给出的状态方程和量测方程基础上空间目标跟踪无论是采用EKF、UKF等非线性滤波方法,还是转换测量卡尔曼滤波(CMKF)等线性滤波方法都不可避免地会存在一定的误差。空间动力学方程约束的目标跟踪利用的是式(5)给出的状态方程,其滤波模型为了充分利用式(6)给出的重力加速度对跟踪中的目标状态进行实时调整,还需对f(X(k))做线性化处理,该处理过程又会带来一定的误差,但由于该目标状态方程更符合空间目标运动规律,该线性化处理所带来的误差是不可避免的,不会对跟踪结果带来负面影响。

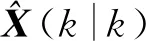
(17)

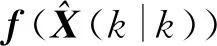
(18)

式中:x1,x2,…,x9分别为式(10)给出的状态向量X(k)中的各元素。

由式(17)可得空间动力学方程约束下的状态一步预测为

(19)

将式(17)和式(19)相减,可得:

(20)

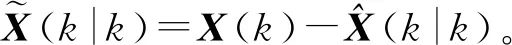
由式(20)可得协方差的一步预测:

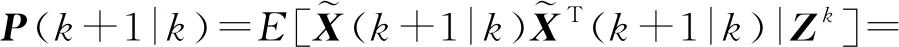
(21)

式中:Q(k)为过程噪声V(k)的协方差矩阵,有

(22)

(23)

新息协方差:

S(k+1)=H(k+1)P(k+1|k)HT(k+1)+RD(k+1)

(24)

式中:H(k)为量测矩阵,RD(k)为直角坐标系下转换量测噪声序列WD(k)的协方差阵[3]。

增益:

K(k+1)=P(k+1|k)H′(k+1)S-1(k+1)

(25)

状态更新方程:

(26)

协方差更新方程:

P(k+1|k+1)=[I-K(k+1)H(k+1)]P(k+1|k)·[I+K(k+1)H(k+1)]T-K(k+1)RD(k+1)KT(k+1)

(27)

式中:I为9×9的单位阵。

4 仿真分析

4.1 仿真环境

本文在仿真条件下对空间密集目标跟踪算法进行验证,可分辨空间密集目标群数据处理过程的流程如图1所示,仿真中相关参数设置如表1所示。

图1 可分辨空间密集目标的群跟踪流程图

表1 仿真参数设置

4.2 仿真结果分析

图2～图4给出了东北天(ENU)坐标系下本文方法、基于距离分割[3]的群目标跟踪、未做群处理直接跟踪的结果对比。图中,实线为目标真实轨迹,点线为量测轨迹,长虚线为滤波轨迹。图5为100次蒙特卡洛实验后的1号目标位置均方根误差图。

图5 1号目标位置均方根误差对比图

相关计算如下:

(28)

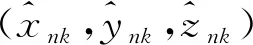
由图2～图4可看出,无论是群目标产生的初期阶段,还是群目标跟踪后期(下降段),利用本文方法的群跟踪航迹平滑度和清晰度都明显优于基于距离分割群跟踪和未做群处理直接跟踪的结果。由图2和图3可看出,在诱饵刚释放的上升段早期,目标密集性较高,本文提出的群处理方法在以某个数据为中心进行分群处理的基础上,还以该目标群内其他数据为中心再次进行判断,因而群目标合并处理的效果更加明显。由图4可看出,随着跟踪时间的延长,目标逐渐从群里分离出去,群目标跟踪就逐渐过渡到多目标跟踪,但根据目标密集情况的不同,可能仍有部分目标需要作为一个群来处理。

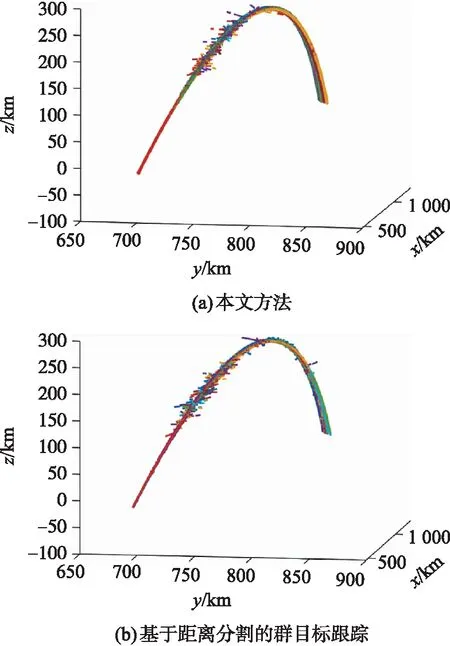
图2 群目标跟踪三维轨迹图

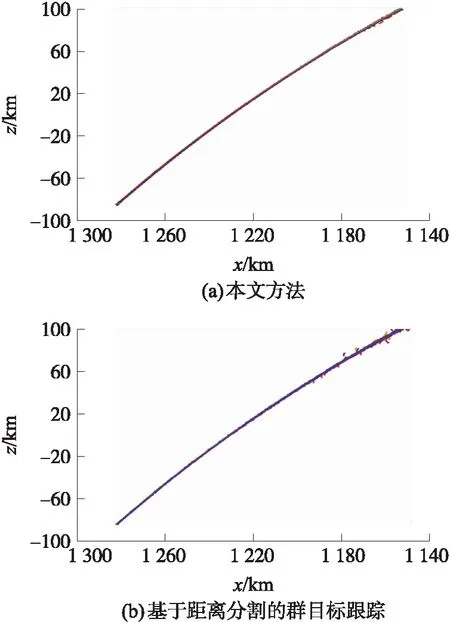
图3 群目标上升段局部轨迹放大图

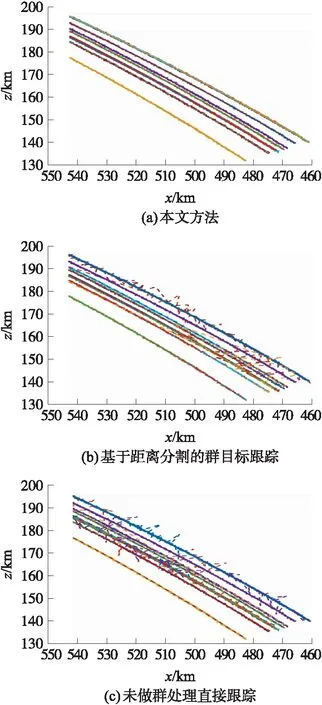
图4 群目标下降段局部轨迹放大图

由图5可看出,100次蒙特卡洛实验所得到的1号目标位置均方根误差由原来的15 m左右降到3 m左右,基于空间动力学方程约束的目标跟踪相比传统方法跟踪精度有较明显的提升。由仿真分析还可看出,本文所提算法在目标密集性较高的场合优势更明显,如果群内目标间距较大或者目标距离均大于设定的群门限,则群处理后仍为多目标跟踪。群处理在密集目标环境下可以起到事半功倍的效果,其能够有效避免密集群目标跟踪早期由于频繁的数据互联错误而导致的短小航迹多、跟踪态势混乱等问题,同时还可以提高群目标跟踪处理速度。

由仿真分析还可看出,本文所提算法在目标密集性较高的场合优势更明显,如果群内目标间距较大或者目标距离均大于设定的群门限,则群处理后仍为多目标跟踪。

5 结论

空间目标群具有运动速度快、密集性高等特点,该情况下多目标数据关联可能会因为关联错误,出现航迹中断、频繁重新起始、交错跟踪等问题,导致短小航迹多、跟踪态势混乱,同时大量数据做关联处理还会对跟踪实时性产生影响。为了有效改善可分辨空间目标群早期的跟踪态势,提高高速目标群的跟踪处理速度和跟踪精度,本文将空间目标特征信息和群跟踪算法相结合,提出了基于全局聚类的群目标分割方法,在此基础上,根据空间目标群中心数据实时构造检验统计量,通过目标与测量数据双向互选提高数据关联的准确性。最后,利用空间目标动力学方程估计的加速度实时修正和协方差闭环反馈循环提高跟踪精度,提升空间密集目标数据处理能力,为后续空间目标轨迹预报提供数据支持。