基于伪标签局部集成投票属性约简*

王东杰

（江苏科技大学 镇江 212003）

1 引言

Pawlak［1］提出的粗糙集理论是经典粗糙集的延伸。它已被证明在数据挖掘［2～3］，人工智能［4］等学科中具有重要作用。

尽管如此，粗糙集理论在实践中仍有许多局限性需要解决。例如基于等价关系的经典粗糙集仅适用于离散数据，而数值数据［5～6］在实际应用中随处可见。基于此，作为广义粗糙集模型的一个重要组成部分，Hu等［7］提出的邻域粗糙集模型在粗糙集理论中取得了巨大成功。

众所周知，属性约简作为粗糙集核心内容之一，在邻域粗糙集中也获得了广泛关注。属性约简就是根据给定的度量准则去除不相关属性，以满足相应的约束条件。广泛接受的属性约简策略包括穷举式算法和启发式算法［8～9］，然而很多穷举式算法和启发式算法将所有样本作为一个整体，忽视了不同样本具有的决策类别不同这一情况。为解决这一问题，Qian等［10］提出的局部邻域粗糙集属性约简算法考虑了不同决策类对不同关键属性的需求。

然而，局部邻域粗糙集属性约简算法仍然面临着以下两个问题：1）经典邻域粗糙集没有关注到半径变化对样本标签的影响，以致于不同标签样本被划分到相同邻域；2）传统的属性约简算法只有一个约束条件，缺乏适用性［11］。为了能够同时解决上述两个问题，笔者利用杨等［12］提出的伪标签策略，设计了一种基于伪标签局部集成投票的约简算法。基于伪标签局部集成投票的约简算法主要步骤：首先，利用k-means聚类计算出伪标签加入到决策系统中；其次，利用启发式算法计算出每个决策类属性重要度，并选取属性重要度最大的属性；最后，利用集成投票机制将合适的属性添加到约简集中［13～20］。

2 基础知识

2.1 领域粗糙集

在粗糙集理论中，一个决策系统可以表示为一个二元组DS=＜U，AT∪｛d｝＞，其中U是所有样本的集合，AT是条件属性的集合，d是决策属性。此外，∀x∈U，d｛x｝表示样本x的标签。给定决策系统DS，当DS中的所有决策值都是离散时，可以定义不可分辨关系INDd为

显然，INDd是一种等价关系。通过INDd可以获得样本U上的划分：

∀Xj∈U/INDd，Xj称为第j个决策类。∀x∈U，包含样本x的决策类表示为［x］d。在传统粗糙集理论中，等价类仅适用于处理离散数据，并不适用于处理连续型数据。为填补这一空白，Hu等［15］提出了邻域粗糙集。邻域粗糙集优势在于：1）邻域可以用数值数据表征样本之间相似性距离；2）通过使用不同的半径可以获得不同的邻域尺度，从而形成多粒度结构。邻域粗糙集中邻域关系的概念可以用条件属性来定义。

定义1给定一个决策系统DS，∀B⊆AT，邻域关系可以定义为

其中ΔB(x,y)指通过B中的条件属性表示样本x和y之间的欧几里德距离，δ是给定半径，且δ≥0。遵循定义1，可以得到如下邻域：

邻域概念不仅可以用于构建粗糙集，还可以用于构建分类器。不同于近邻分类方法，邻域分类器并不指定待测样本的邻居个数，而是采用设定半径的方式找到满足约束条件的待测样本的邻居。可以设计如算法1所示的邻域分类器。

算法1邻域分类器（NEC）

输入：训练数据构成的数据表DS=＜U，AT∪｛d｝＞，B⊆AT，半径δ，待测样本y。

输出：y的预测分类标签：Pre（By）。

步骤1：∀x∈U，计算样本之间距离D（Bx，y）；

步骤2：计算测试样本的邻域δ（By）；

步骤4：Xk=arg max{Pr(Xi|δ(y)):∀Xi∈U/INDd}；

步骤5：根据Xk找到对应的标签，并赋值给Pre（By）；

步骤6：输出Pre（By）。

通过比较真实标签与邻域分类器分得的结果，邻域决策错误率可以定义如下。

定义2对于决策系统DS，∀B⊆AT，邻域决策错误率可定义为

显然，邻域决策错误率的值越小，算法的分类性能越好。

2.2 伪标签邻域粗糙集

经典邻域粗糙集没有关注到半径变化对样本标签的影响，以致于不同标签样本被划分到相同邻域。为解决这一难题，杨等［12］提出伪标签策略。与邻域决策系统类似，伪标签邻域决策系统可以表示为DSP=＜U，AT∪｛d｝∪dP＞，dP是伪标签属性。∀x∈U，d（Px）表示样本x的伪标签值。

定义3给定一个伪标签决策系统DSP，∀B⊆AT，伪标签邻域关系定义为

根据定义5，可以得到如下伪标签邻域：

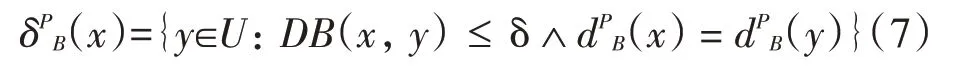
3 属性约简

属性约简也称为特征选择，其目的是通过某些给定约束删除冗余属性。通过这一策略，能够大大降低学习的难度和时间消耗。近年来，根据实际需求，已有大量学者提出了多种度量准则，例如近似质量［15］、邻域决策错误率［16］等，笔者选择邻域决策错误率作为属性约简的约束条件。

3.1 传统启发式属性约简

在启发式属性约简中，给定一个决策系统DS，∀B⊆AT和∀a∈AT-B，如果NDER（B，d）＞NDER（AT，d），属性a对分类精度的提高没有贡献；如果NDER（B，d）≤NDER（AT，d），属性a提高了分类精度。因此根据邻域决策错误率，可以得到如下属性重要度：

以下算法2给出了一个求解启发式约简的具体描述。

算法2启发式算法

输入：决策系统DS=＜U，AT∪d｝＞，半径δ。

输出：一个邻域决策错误率约简red。

步骤1：计算NDER（AT，d）；

步骤2：red←∅；

步骤3：WhileNDER（B，d）≤NDER（AT，d）

1）∀ai∈AT-B，计算属性ai的重要度SigNDER（ai，B，d）；

2）选出一个重要度最大的属性b，令red=red∪｛b｝；

3）计算NDER（B，d）；

End While；

步骤4：返回red。

算法2的时间复杂度为O（|U|2×|AT|2），|U|为论域中样本数目，|AT|为条件属性数目。

3.2 伪标签局部集成投票属性约简

经典邻域粗糙集没有关注到半径变化对样本标签的影响，以致于不同标签样本被划分到相同邻域。另外，传统局部算法只有一个适应度函数，导出的约简仅考虑一个约束，致使约简结果缺乏通用性。为了同时应对上述难题，笔者提出了一种基于伪标签局部集成投票的约简算法。以下给出伪标签局部集成投票邻域决策错误率的定义。

定义4给定一个伪标签决策系统DSP，∀B⊆AT，决策类Xi的伪标签邻域决策错误率定义如下：

给定一个决策系统DS，∀B⊆AT，∀Xj∈U/INDd，∀a∈AT-B，可以得到如下属性重要度：

以下算法3给出了一个求解伪标签局部集成投票属性约简的具体描述。

算法3伪标签局部集成投票算法

输入：决策系统DSP=＜U，AT∪｛d｝∪dP＞，半径δ。

输出：约简R。

步骤1：计算NDERP（AT，d）；

步骤2：R←∅；

步骤3：For d=1 toq//q为决策类个数

1）∀ai∈AT-B，计算属性ai的重要度；

2）根据每个决策类Xi选出一个重要度最大的属性b并记录每个属性的出现次数。

End For

步骤4：投票选择频率最高的属性：c；

步骤5：R=R∪｛c｝；

步骤6：WhileNDERP（B，d）≤NDERP（AT，d）

Go to step 3；

End While

步骤4：返回R。

算法3的时间复杂度为O（q×|U|2×|AT|2），其中q为决策类的数目。

4 实验分析

为了验证上述所提伪标签局部集成投票算法的有效性，笔者从UCI数据集中选取了五组数据，数据的基本描述如表1所列。

表1 数据集描述

实验采用了5折交叉验证的方法，并且选取了十个不同的半径δ，其值分别为0.05，0.10，…，0.5。试验过程中将实验数据中的样本平均分成5份，即U1，U2，…，U5。第一次使用U2∪U3…∪U5作为训练集，使用U1作为测试集；第二次使用U1∪U3…∪U5作为训练集，使用U2作为测试集；依次类推，第五次使用U1∪U2…∪U4作为训练集，使用U5作为测试集。本组实验选取了邻域决策错误率作为约简的度量准则。实验结果如图1所示。

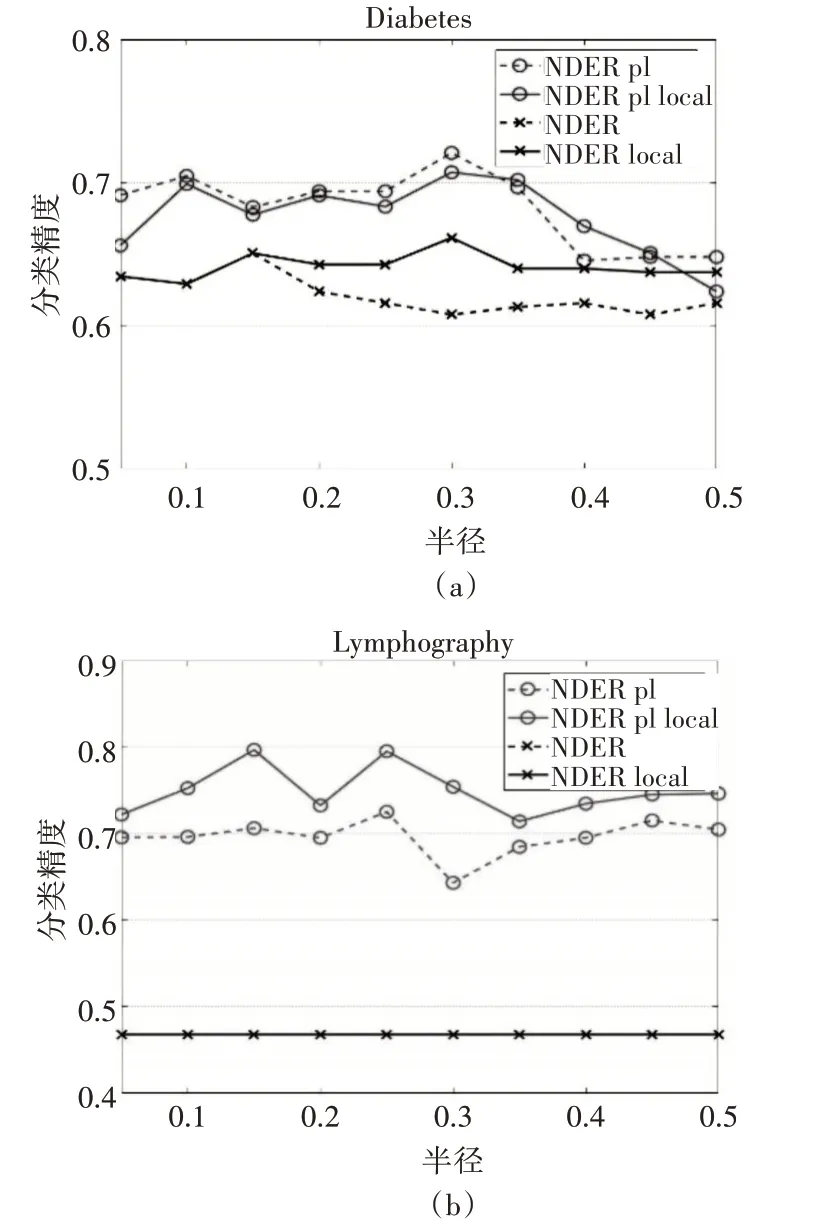
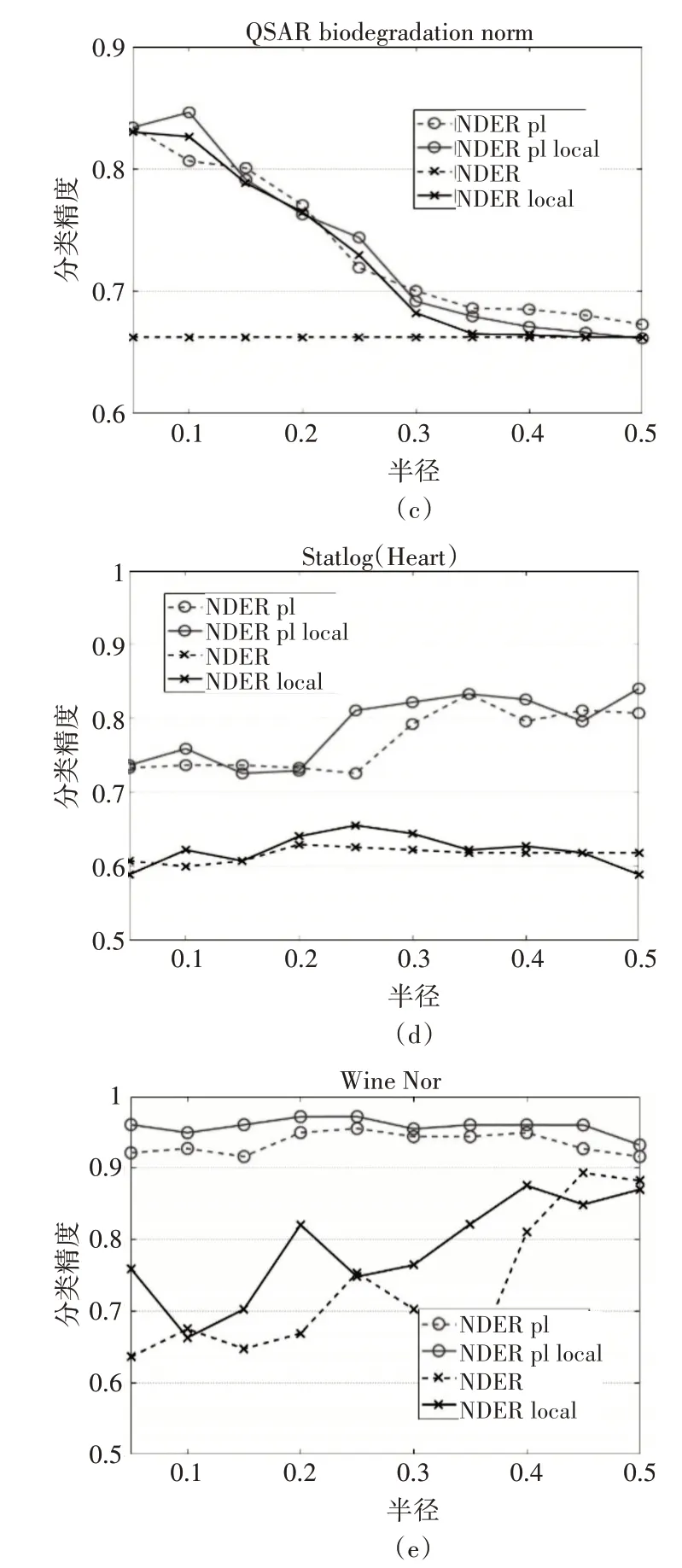
图1 分类精度对比

在以下的结果图中，用“NDER”，“NDER local”，“NDER pl”，“NDER pl local”分别表示邻域决策错误率约简、局部邻域决策错误率约简、伪标签集成投票邻域决策错误率约简、伪标签局部集成投票邻域决策错误率约简。

4.1 邻域决策错误率（NDER）上约简结果的分类精度对比

观察图1可以发现，在10个半径下，不难得出如下结论。

1）与传统约简相比，伪标签局部集成投票的约简算法的分类性能更好；

2）在四种算法的比较中，伪标签局部集成投票算法的分类精度最高。

4.2 邻域决策错误率（NDER）下约简的时间消耗对比

通过观察图2可以发现：

图2 时间消耗对比

1）在四种约简算法中，利用局部约简求解总体上需要更多的时间消耗。这主要是因为相较于传统算法，局部算法需要考虑每一个决策类的变化；

2）与传统局部算法相比，伪标签局部集成投票算法明显降低了时间消耗。

通过观察表2可以发现：与补加伪标签集成投票的算法相比，加上伪标签集成投票的算法大体上降低了时间消耗。

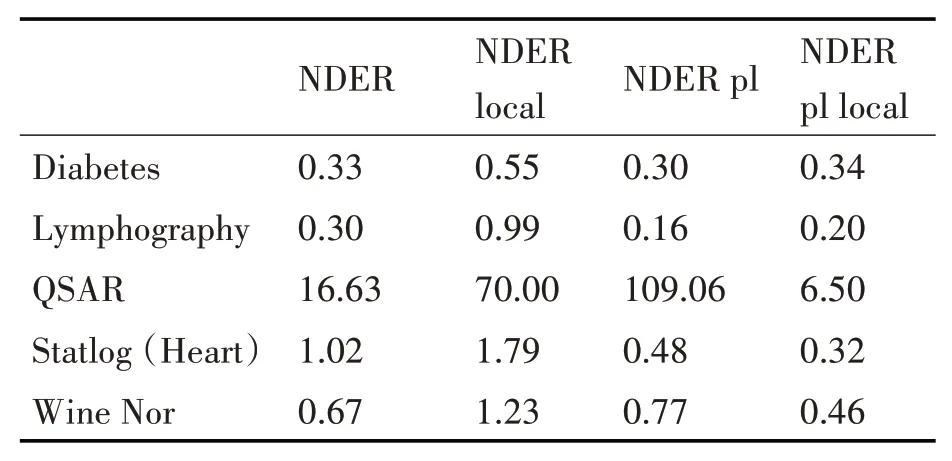
表2 平均约简求解时间消耗对比（单位：s）

5 结语

为了防止不同标签样本落入相同邻域以及增强约简求解的通用性，笔者提出了一种伪标签局部集成投票算法。通过实验分析表明，相较于传统算法，伪标签局部集成投票算法可以明显提高分类性能，并且降低时间消耗。在此基础上，笔者将进一步讨论以下问题。

1）文中算法的时间消耗仍然较高，今后可以尝试进一步降低时间消耗。

2）文中算法模型仅使用在邻域粗糙集，今后可以尝试使用在模糊粗糙集等模型。