基于中心对称多胞体的四旋翼无人机执行器故障检测

杨雨薇，胡 陟，章 伟

(上海工程技术大学 机械与汽车工程学院，上海201620)

0 引 言

近年来，四旋翼无人机由于其体积小、机动性强、具有灵活性等特点，得到了研究者们的广泛关注和研究，无人机的诸多性能指标飞速提高，控制技术得到极大的发展，其在军事和民用领域发展十分迅速。在日常的生活中如航拍、空中载物、侦察监测等各个方面逐步普及［1］。由于无人机内部结构精细，同时存在机载环境的温度变化，机械振动等客观因素，无人机较易发生损伤或失效，导致系统出现故障［2］。为了更大范围的降低损失，快速检测判断无人机是否发生故障，保证系统安全性尤为重要［3］。

无人机故障通常分为执行器故障与传感器故障。目前为止，对具有执行器故障系统的研究和四旋翼无人机执行器故障问题有很好的借鉴意义。Chadli等人设计了H／H∞观测器对故障进行观测［4］；为了提高观测器对噪声和干扰的鲁棒性，汤文涛、胡志坤等人通过设计未知输入观测器对干扰和噪声进行解耦，实现了故障检测与分离［5］；王振华等人通过将故障视为辅助状态向量来构造增强系统，基于增强系统设计观测器，解决了离散线性系统描述符系统的执行器故障估计问题［6］；叶慧等人采用小波变换，不依赖系统模型，提高了故障的可分离性［7］；宫勋等针对四旋翼无人机可能存在执行器故障的情况，使用并行降维观测器构建检测与重构算法，有效地实现对执行器故障的检测并将出现故障的执行器进行隔离，此外该控制算法的应用可以有效地抑制扰动［8］；有文献提出了一种新的基于自适应观测器的执行器故障估计方法［9］。然而以上文献考虑的问题主要集中在执行器故障的稳定控制问题，并且取得了很好的控制效果，但是四旋翼无人机性能没有得到足够的重视。文献针对执行器故障检测，提出基于中心对称多胞体的一种故障诊断与分离的方法，根据一般的离散数学模型设计未知输入观测器，与原值对比得到残差信号，基于中心对称多胞体形成故障范围阈值，通过残差与阈值的比较，完成故障诊断［10］。但该文献也只考虑了普通执行器的故障问题，通常四旋翼无人机的模型为一个六维的连续方程组，本文在此基础上，完成了模型的离散化与维度的扩展，并通过仿真实验证明，该算法对于四旋翼无人机的2种不同执行器故障模型的检测是有效的。

1 四旋翼无人机系统物理模型建立

为了便于四旋翼无人机的数学模型建立，且不失一般性，可做如下假设［11］:

（1）四旋翼无人机为刚性结构，运动过程中质量保持不变；

（2）四旋翼无人机结构完全对称；

（3）地面坐标为惯性坐标系，不计重力加速度随高度的变化，不计地球曲率；

（4）电机的电压-力矩函数为线性函数；

（5）四旋翼无人机的质心严格位于结构中心。

四旋翼无人机飞行姿态动力学模型，对其泰勒展开并做适当的截尾处理得到如下系统模型［12］，式（1）:

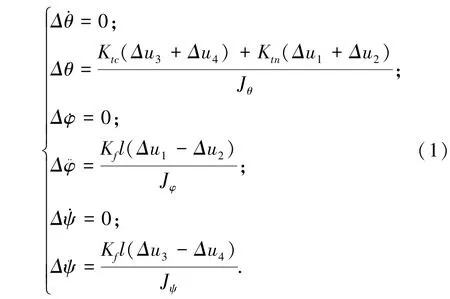
将模型（1）表示成一般的线性动态方程，式（2）:

其中，A、B、C为适当维数的系统矩阵。状态向量为输出向量 为y＝［θ φ ψ］T； 控 制 输 入 为u＝［Δu1Δu2Δu3Δu4］T。

2 四旋翼无人机执行器故障系统数学模型

2.1 执行器故障特征描述

执行器由于外部干扰，润滑失效等现象会产生故障。按执行器故障的特点与严重程度，可分为突变加性故障、缓慢时变故障。

四旋翼无人机有多个执行器，第i个执行器发生故障时，其数学模型可表示为:

（a）突变加性故障fi＝b，其中，b为常量。

（b）缓慢时变故障fi＝ηi（t-ts），其中，ηi表示第i个执行器的故障系数，为常量；ts为故障的起始时刻；t为故障发生的任意时刻。

2.2 中心对称多胞体

中心对称多胞体的符号定义及其特性:

中心对称多胞体集合ℑ⊂Rn是一种特殊的凸多面体，首先给出中心对称多胞体的数学定义:

定义一个r维中心对称多胞体ℑ⊂Rn定义为以p∈Rn为中心的r维单位立方体Br＝［-1，+1］r的仿射变换，即式（5）:

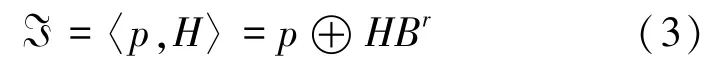
其中，矩阵H∈Rn×r称为ℑ的生成矩阵，其决定了ℑ的形状和大小。

中心对称多胞体的主要性质［14］有:

性质:给定中心对称多胞体ℑ＝〈p，H〉，则有式（4）～（6）:

其中:p，p1，p2∈Rn，H，H1，H2∈Rn；⊙表示线性映射；L∈Rl×n为适当维数的矩阵；H-∈Rn×n是对角矩阵；其对角元素为

2.3 四旋翼无人机带有执行器故障的模型

首先对系统（2）做离散化处理:

其中，x（k）∈Rnx是状态向量；u（k）∈Rnu是输入向量；y（k）∈Rny是输出向量；D1，D2为已知适当维数的矩阵；ω（k），υ（k）分别为系统受到的未知干扰与噪声。

考虑系统存在执行器故障时的离散时间线性模型表示为式（8）:

式中，F为已知的故障矩阵，f（k）∈Rnf表示执行器故障。

假设，四旋翼无人机系统有且只有一个执行器发生故障，第i个执行器发生故障时的系统模型为式（9）:

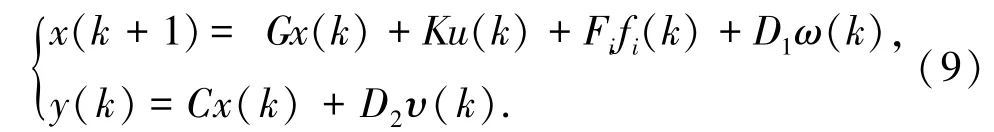
其中，Fi表示故障矩阵F的第i列。

3 执行器故障检测

3.1 未知输入观测器设计

未知输入观测器本质上是针对不确定系统设计的观测器，通常这类不确定系统可以描述为式（10）:

该类系统与严格正则的线性系统相比多出了一个Ed的未知输入项。式中，E为未知输入分布矩阵，d为未知干扰向量。在未知输入观测器的设计中，为了消除未知干扰d的影响，需要对干扰进行重构并完成解耦。

根据系统（7），得到:

为了消除干扰ω（k），必须满足式（12）:

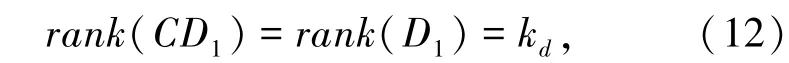
才能达成完全重构干扰项的目的。在这个条件下，存在Mcd，式（13）:

用Mcd同时乘以式（11）的左右两边，得式（14）:

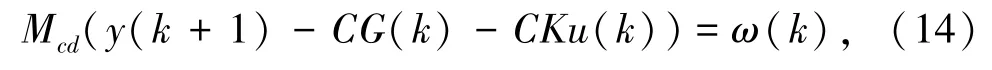
即可以估计得到式（15）:

设计Luenberger观测器，式（16）:

观测器方程中，无法事先知道y（k+1）。故假设:

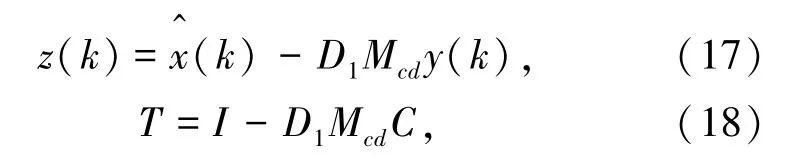
代入（15）得式（19）:

令P＝TG-LC，J＝TK，Q＝D1Mcd，故未知输入观测器方程为可以简化为式（20）:

残差信号可以表示为式（21）:

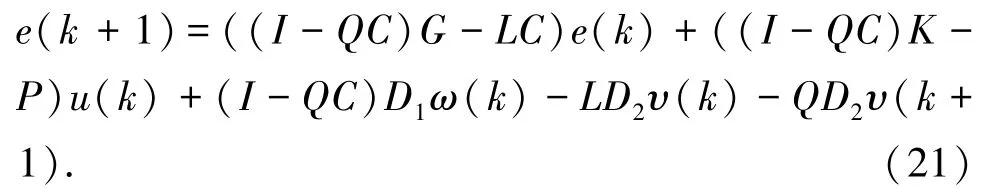
命题3.1［10］如果存在（I-QC）D1＝0，可得式（22）:

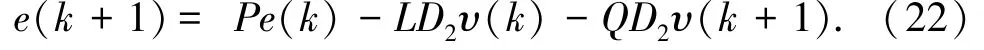
命题3.2［15］方程（I-QC）D1＝0的充要条件为式（23）:

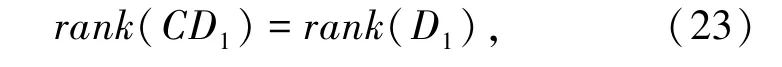
故有:

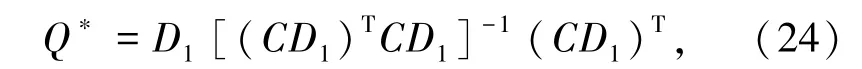
式（20）是系统（7）的未知输入观测器的必要条件为:rank（CD1）＝rank（D1），（C，G1）矩阵对可观测，

其中:

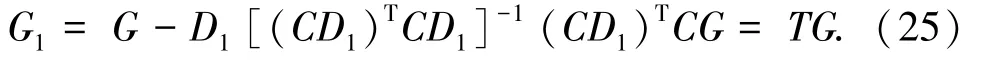
满足以上条件的情况下，可以计算出相应的未知输入观测器设计参数矩阵。

3.2 四旋翼无人机执行器故障的区间估计

考虑带有第i个执行器发生故障的系统（9），设计相应观测器进行故障解耦。设计观测器如式（26）:

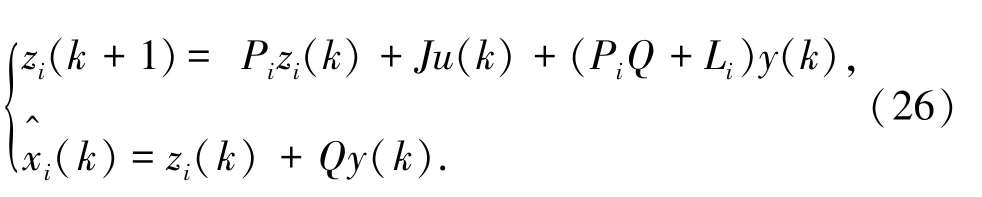
式中，zi（k）∈Rnx表示第i个未知输入观测器的状态变量表示第i个未知输入观测器的状态估计值；矩阵Pi，Q，Li为带设计矩阵，且Pi，Li满足式（27）:

由式（21）可知，第i个执行器故障时，状态估计误差为式（28）:

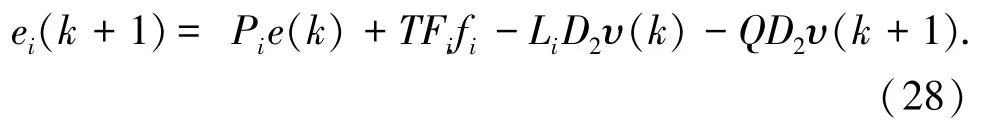
已设计好的观测器的残差生成器为式（29）:

在进行故障检测之前，首先需要满足以下假设:

（1）系统（9）的未知输入干扰项满足:

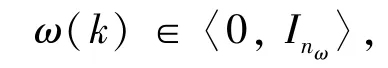
（2）系统（9）的噪声项满足:

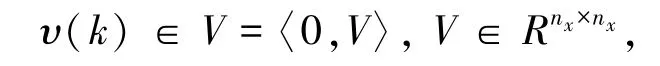
（3）系统（9）的状态估计误差初值满足:

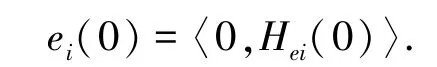
命题3.3［10］对于离散系统（9），若满足上述假设，则存在合适的观测器增益Li，使得k+1时刻地估计误差为ei（k+1）∈〈0，Hei（k+1）〉，残差满足ri（k）∈〈0，Hri（k）〉，其中，中心对称多胞体的生成矩阵为式（30）和式（31）:

通常在使用中心对称多胞体对故障进行检测分析时，生成多胞体ℑ的维数会不断地增加，因此，需要对其进行完成降维处理［16］。所以在无故障的情况下，残差满足式（32）:

通过中心对称多胞体生成不考虑故障时的最大包络，将其作为阈值。

4 仿真实验

本次实验采用无人机相关参数在MATLAB上进行仿真。取仿真采样周期为Δt＝0.01 s，则离散方程（7）中相应的系统矩阵为:

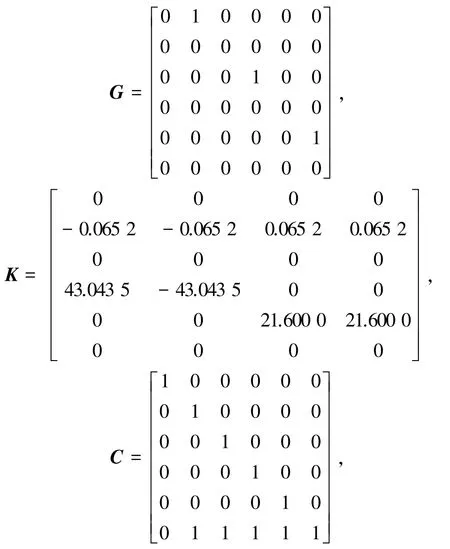
在本次研究中，取［16］:

在满足McdCD1＝Ikd×kd的前提下解Mcd，Q，T:

四旋翼无人机模型系统满足（I-QC）D1＝0，矩阵G1为:

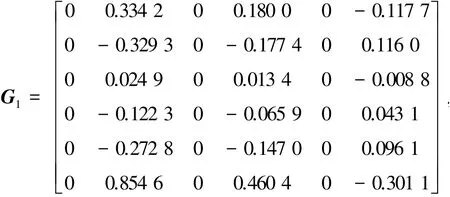
经检验，G1满足（C，G1）可观测的假设。

通过MATLAB工具箱对合适的极点进行极点配置，即可以求得观测器的增益矩阵L以及P为:

假设执行器1在k＝50时发生突变故障，执行器2在k＝50时发生缓慢时变故障:

当执行器1发生突变故障时仿真结果如图1所示。显然，图1中存在有残差超过相应的阈值范围，因此本文研究的算法可以适用于执行器的突变故障分析。当执行器2发生缓慢时变故障时，故障诊断结果如图2所示，同样地，发生缓慢时变故障时依旧能够很快速地诊断出该故障。

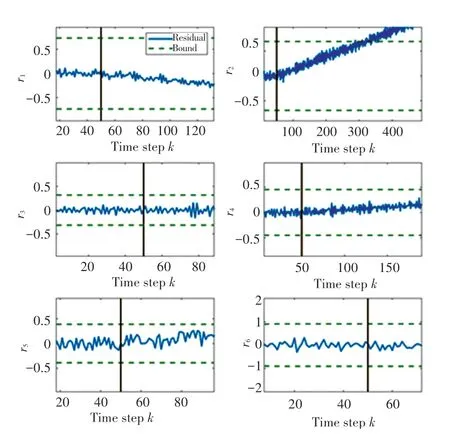
图1 突变故障诊断结果Fig.1 Abrupt fault diagnosis result

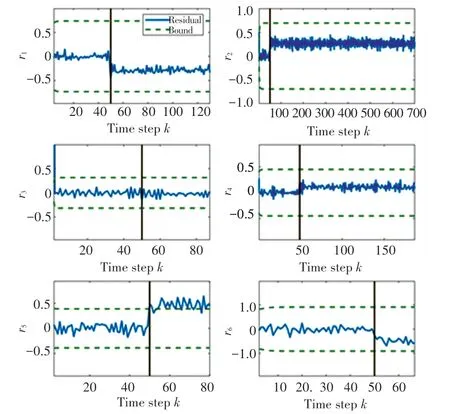
图2 缓慢时变故障诊断结果Fig.2 Slow time-varying fault diagnosis result

5 结束语

本文针对发生不同执行器故障的四旋翼无人机提出了基于中心对称多胞体形成阈值的方法进行故障检测。首先根据实际力学方程建立无人机系统模型，利用泰勒展开得到无人机的线性动态方程。通过设计全维未知输入观测器得到执行器的故障估计，利用中心对称多胞体形成故障阈值区间，通过分析比较故障值与故障区间对执行器故障进行检测。根据本文设计的检测算法，在MATLAB平台上成功的检测了执行器发生的两种不同故障。本文研究的故障类型仅限于突变故障和缓慢时变故障，其它类型的故障还有待研究。