二阶时变时滞多智能体系统快速一致性算法

张婷婷，张 伟

(上海理工大学 光电信息与计算机工程学院，上海200093)

0 引 言

近年来，随着人工智能和分布式协调控制理论的发展，多智能体系统的协调控制也吸引了大批研究者的关注和研究。多智能体系统应用于多领域，如分布式传感器网络［1］、编队控制［2-4］、群集［5］、协同控制［6］和分布事件触发［7-8］等。实现多智能体网络协调控制，需要各个智能体状态达到一致。因此，一致性问题是研究多智能体系统的基础和核心。在保证多智能体系统的稳定性前提下，提高系统的动态性能也具有一定的研究意义。

多智能体系统的动态性能，即多智能体的一致性收敛速度。提高收敛一致性，无疑能够提高系统的通讯能力及性能。文献［9］中，Olfati提出了一种超高速信息网络的算法，该算法可以在小网络上以惊人的速度达到多智能体一致性，并且验证了收敛速度由通信的代数连通性决定，为研究快速一致性提供了有力的理论基础。基于此理论，She［10］等人提出基于局部信息的多智能体系统，引入PI控制器设计快速一致性算法，给出智能体快速收敛的充分条件。文献［11］针对分布式控制与大系统的快速一致性，基于双跳网络提出快速一致性算法，使得多智能体系统的收敛速度更快。文献［12-15］研究了二阶以及高阶系统的多智能体快速收敛一致性算法。由于通讯约束，智能体之间交互信息时产生时滞，研究者从网络通讯拓扑图着手，引入多跳网络设计一致性算法，且利用频域法分析系统收敛条［16-19］。文献［20］分析了带有时变时滞的多智能体一致性，引入小增益理论，基于频域的角度分析系统的稳定性。受文献［13，20］的启发，本文从频域的角度分析带有时滞的快速一致性。虽然随着网络的发展，传输速度越来越快，但是智能体传输的过程中，依旧会存在时滞，并且实际过程中的时滞可能是时变的，所以对研究时变时滞多智能体系统具有实际意义。

本文将时变时滞的二阶多智能体网络系统作为研究对象，基于频域的角度分析二阶时变时滞多智能体系统，且时滞是具有上界的，任意变换的。本文研究结果为:通过一致性协议改进算法，基于频域理论，小增益理论，矩阵论和图论等，推导得到了使系统快速收敛一致性的充分条件；相较于已有的控制协议，本文改进的算法能够使系统快速渐近收敛一致。

1 预备知识

1.1 图论

本文基于无向网络拓扑图，研究多智能体一致性问题。研究此类问题需要利用如下的图论知识和一致性问题的描述。

假设，用图G＝（V，ε，A）来表示所描述的多智能体网络系统（Multi-Agent Systems，MAS）的无向拓扑图。其中是节点集的N索引值，ε∈V×V为图G的边集。A＝［aij］RN×N（R表示实数集）为图G的邻接矩阵，并且为非负元素。其中i，j∈V（i，j分别表示智能体i和智能体j）。当aij＞0时，代表智能体i和智能体j之间有信息传递；而aij＝0表示智能体i和智能体j之间没有信息传递。考虑本文所研究的是无向图，则邻接矩阵A是对称的。若在任意2个智能体i，j∈V之间存在一条 路 径，则 称 图G为 连 通 图。 令Ni＝，表示智能体i的邻居集。degi＝表示智能体i的度，定义度矩阵D:＝那么图G的拉普拉斯矩阵LG＝D-A。拉普拉斯矩阵描述节点与边的关系，且LG＝[lij]∈RN×N，其中:

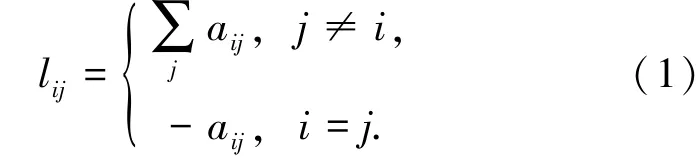
由于系统的拓扑图为无向图且连通，则拉普拉斯矩阵是对称且为正半定矩阵。若λi∈的特征值，则根据拉普拉斯矩阵的性质可得:

1.2 模型描述

假设有N个二阶多智能体系统，每个智能体的动态方程为:

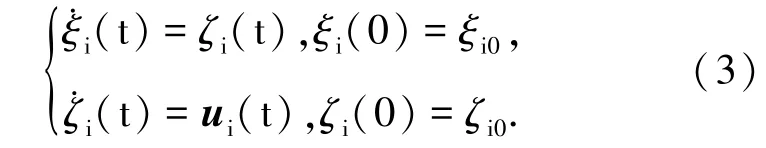
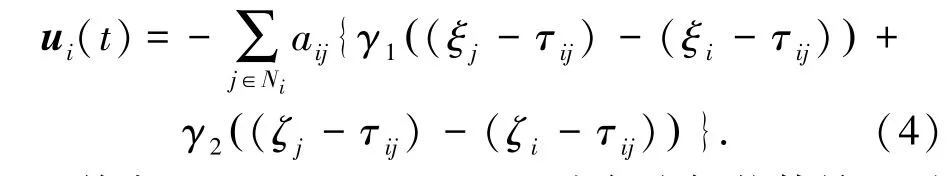
其中，γ1＞0；γ2＞0；τij为每个智能体输入时变时滞；考虑到图G为无向图且连通，则τij＝τji，令若系统在一致性算法式（4）控制输入下，使得智能体状态达到一致性，则系统满足如下条件:

2 主要结果

为了提高体统的收敛速度，本文引入PI控制器，基于式（4）的控制输入提出如下快速一致性算法:

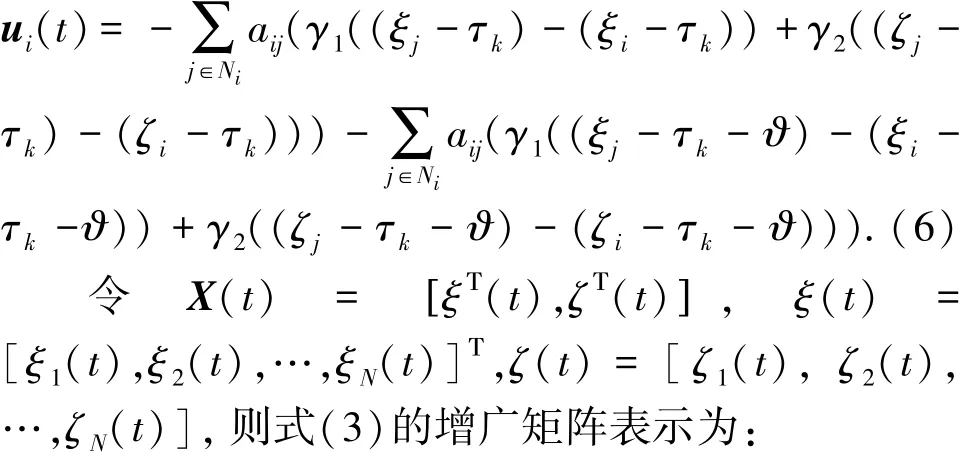
设系统初始值为0，对式（7）进行拉普拉斯变换可得:

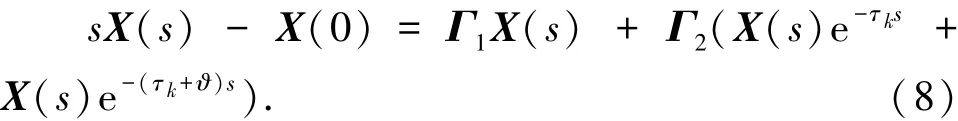
因此，系统的特征方程为:

为了保证系统的稳定性和连通性，需使用如下引理。

引理1［21］当初始值为时，设则系统在一致性算法式（4）的控制输入，使得智能体收敛一致满足的条件为:

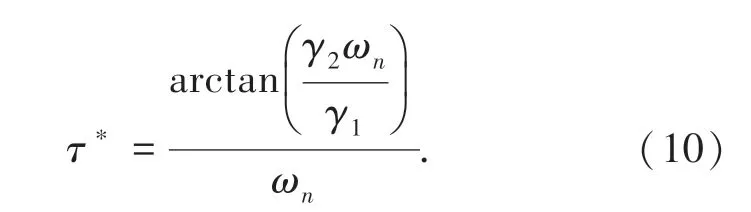
其中，τ*为时滞的上界。

引理2［22］记时滞算子υτk+ϑ:＝ξ（t）-ξ（t-τk-ϑ），υτk:＝ξ（t）-ξ（t-τk），υi:＝υτk+ϑ+υτk。 定义 算 子Δf:＝（Δ（υ）-1）°（1／s），Δ（υ）＝是以τm*为上界的诱导增益，记诱导增益为‖Δf‖∞，‘°’为合成符号，则有

基于引理1与引理2，定理1给出了系统在一致性算法式（6）的控制输入情况下，使智能体状态达到一致的稳定条件。

定理1若连通拓扑图是无向连通的，具有时滞的二阶系统在快速一致性算法式（6）的控制协议下，使得智能体状态达到一致，则满足如下条件:

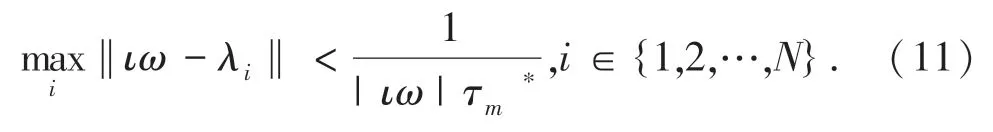
其中，ι为虚数单位。

证明 二阶系统可由线性时不变系统和时变时滞算子表示，其线性时不变系统与时变时滞算子连接如图1所示。

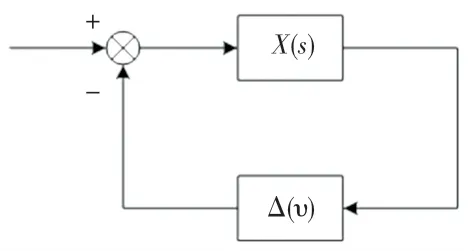
图1 线性时不变系统与时变时滞算子连接图Fig.1 Connection graph of linear time invariant systems and time varying delay operators

图1中，X（s）表示系统的时不变系统矩阵，Δ（υ）为系统的时滞算子。

根据引理2，式（7）的状态空间表达式为:

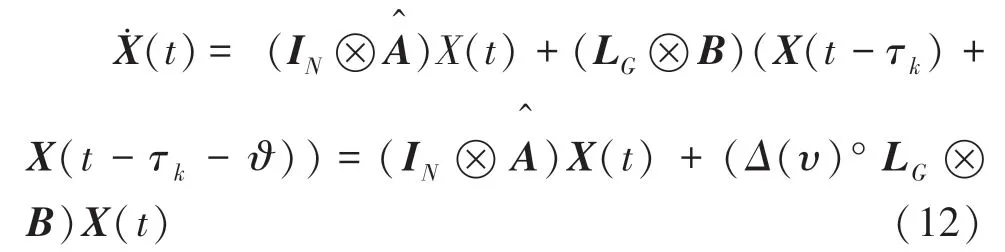
由于LG为对称矩阵，引入酉矩阵U，则根据Laplace矩阵特性可得:

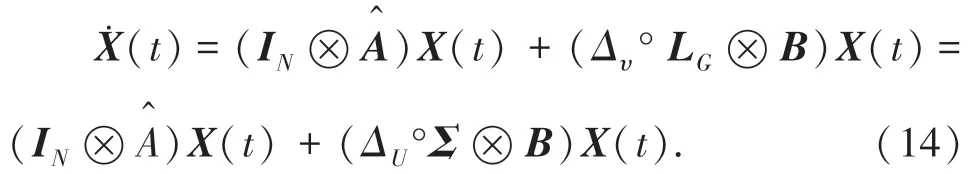
将式（14）进行Laplace矩阵变换，可得到:

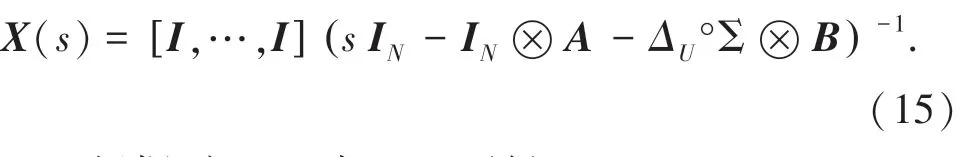
根据引理2，式（15）可得:

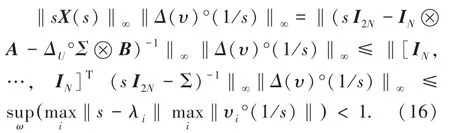
由式（16）可推出式（17）:

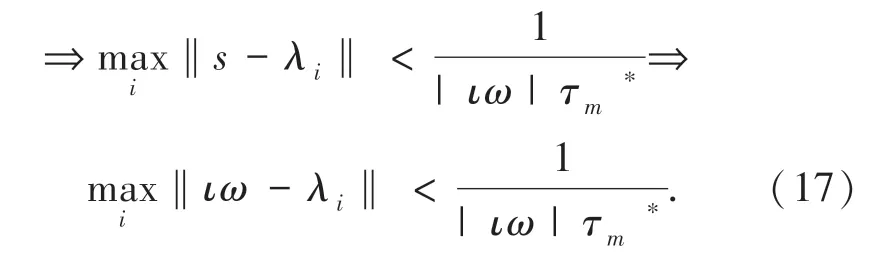
系统基于定理1的情况下，定理2为系统在一致性算法式（6）的控制输入提供了快速收敛充分条件。

定理2 系统在一致性算法式（6）的控制协议下，使系统快速收敛一致的区间为ϑ∈（0，δ），其中δ满足:

证 明 由式（9）可得系统特征方程等价于下式:

根据拉普拉斯矩阵的性质可知，LG的特征λ1＝0，且Re（λi）＞0，i＝2，…，N，则式（18）等价于:

将式（23）取极限可得:

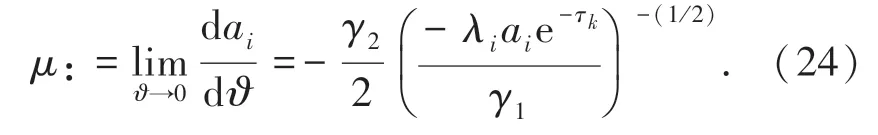
其中，μ为实数部分微分的极限值。当ϑ＞-τk时，ai＜0，则μ＜0。 由局部保号性定理知，存在去心领域内当ϑ＝0时当＜0，即单调递减。若使系统达到快速一致性，则δ满足ai｜ϑ＝δ＝ρ并使其达到最小值。将系统的根代入式（21）得:

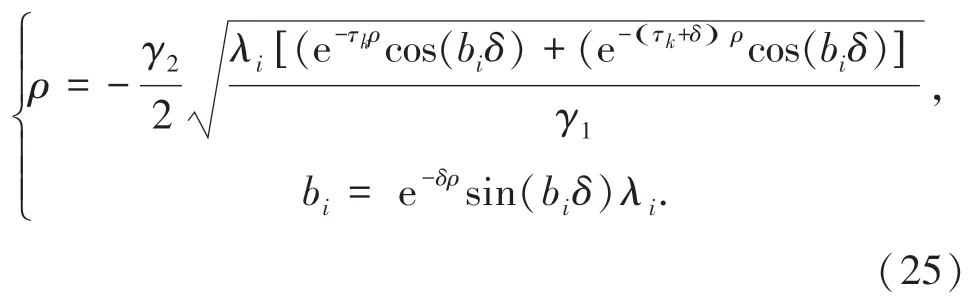
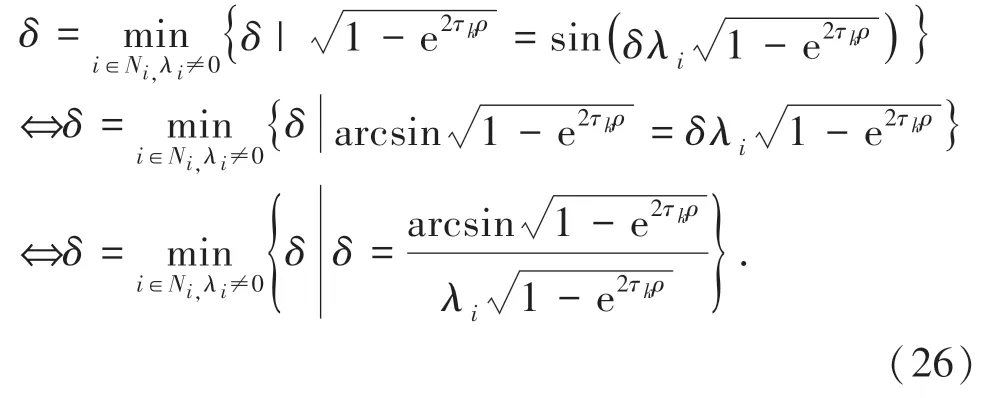
3 仿真分析

为了验证定理1和定理2的有效性，本文以环形网络拓扑结构为例进行验证。通讯网络拓扑图G，共有8个智能体，如图2所示。

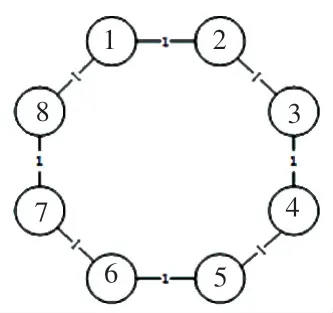
图2 系统网络拓扑Fig.2 The system of network topology

由图2的通讯网路拓扑图可得系统的拉普拉斯矩阵为:

（1）时变时滞为τk＝0.3713*et／（1+et）。 由定理2可计算δ＝0.186，ϑ∈（0，0.186）。 系统分别在控制算法式（4）和式（6）的控制输入下进行仿真，其位移状态变化量的仿真如图3和图4所示。

对仿真图3和图4分析得出，二阶时变时滞多智能体系统在一致性算法式（4）和式（6）的控制输入下，智能体的状态可以达到一致。根据智能体达到一致性的最初时间τ0对比发现，系统在一致性算法式（6）的控制输入下，比系统在一致性算法式（4）控制输入下收敛速度更快。

图3 系统在一致性算法式(4)控制输入下的仿真Fig.3 The simulation diagram of the system in control decision(4)is given

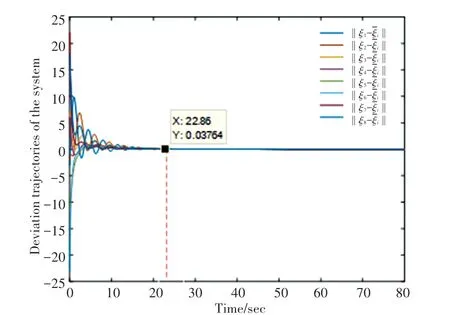
图4 系统在一致性算法式(6)控制输入下的仿真Fig.4 The simulation diagram of the system in control decision(6)is given

（2）时变时滞为τk＝0.3713*et／（1+et）。 若令δ＝0.3，ϑ∈（0.18，0.3），系统在一致性算法式（6）控制输入下，位移状态变化量的仿真如图5所示。τ0表示达到一致性的最初时间。当取δ＝0.3＞0.186时，系统在τ0＝57.27s时达到一致性；在τk不变的情况下，系统在δ＝0.3＞0.186时达到一致性，但达到一致性的速度小于δ＝0.186。 由此实例证实定理2的有效性。

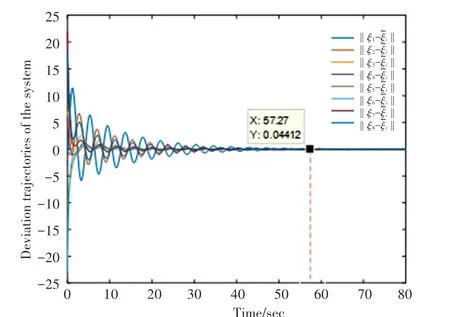
图5 系统在控制协议(4)的仿真Fig.5 The simulation diagram of the system in control decision(4)is given

（3）时变时滞为τk＝0.5*et／（1+et）＞τ*，取参数δ＝0.186、ϑ∈（0，0.186），系统在一致性算法式（4）和式（6）的控制输入下的仿真如图6和图7所示。从图中发现，系统位移状态变量是发散的，系统不能达到一致。而此时的τk的最小值大于τ*，导致系统的不稳定。由此可说明，定理1是合理并且是有效的。

图6 系统一致性算法式(4)控制输入下的仿真Fig.6 The simulation diagram of the system in control decision(4)is given

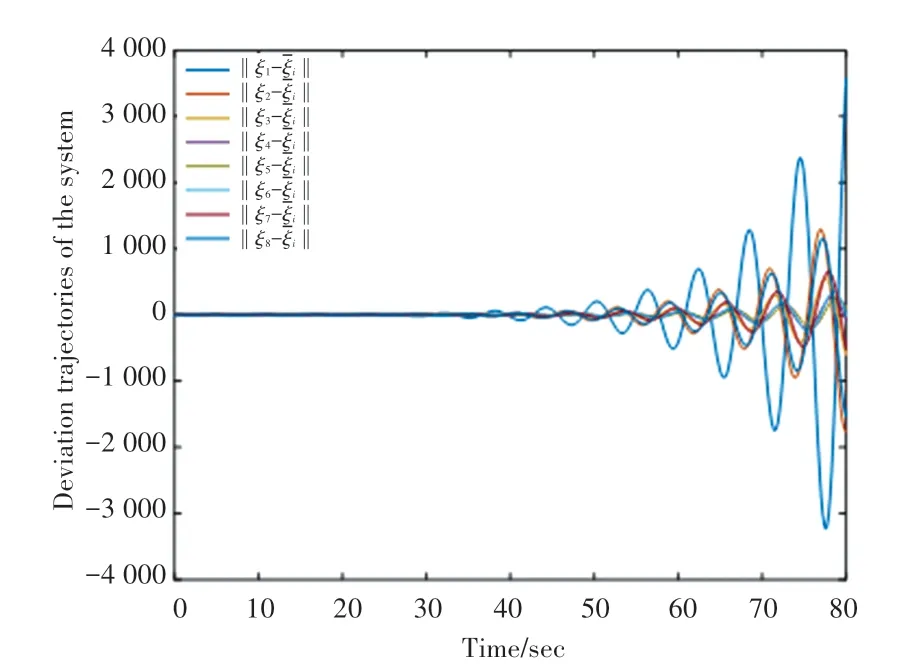
图7 一致性算法式(6)控制输入下的仿真Fig.7 The simulation diagram of the system in control decision(6)is given

根据仿真实例，系统在一致性算法的控制下分析结果如下:

（1）二阶时变时滞系统在时滞上界相同（其时滞上界为引理1计算所得），δ取值相同时，系统在改进后的一致性算法式（6）的控制输入下，首次趋于一致性的时间比系统在已有的控制算法控制输入下快，表明改进后的控制算法的有效性。

（2）二阶时变时滞系统在时滞上界相同（其时滞上界为引理1计算所得），δ大于定理2所计算的值时，系统在改进后的一致性算法控制输入情况下达到一致，但不是最快。

（3）二阶时变时滞系统的时滞上界大于引理1计算出的时滞且δ取值相同时，系统在一致性算法式（4）和一致性算法式（6）控制输入下都会发散。

综上所述，证明了本文提出快速一致性算法的有效性。

4 结束语

本文基于传统的一致性，提出快速一致性算法，结合图论、控制理论和矩阵论，证明了改进后的控制协议的合理性和有效性。利用MATLAB验证了时变时滞的二阶多智能体的快速收敛一致性。本文的研究方向针对连续二阶系统，根据系统的复杂性，后续研究方向是将控制协议推广到带有时滞的离散系统和高阶系统中。