基于绝对节点坐标法的气动软体驱动器建模
陶羽玲,赵春花,鲍康文
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
到目前为止,机器已经逐步代替了人工,生活中到处都充满了机器人的身影。随着市场需求的增大及对生产品种、种类要求增多,人们对机器人末端执行器的要求越来越高[1-2]。传统的机器人末端执行器为刚性执行器,存在硬度大、整体结构笨重且构型复杂等问题,在抓持一些表面易碎的物体如鸡蛋、玻璃器皿、新鲜的瓜果蔬菜等时,对抓取方式及抓取力的大小等要求较高;另外,现在的生产呈现一种多批量、小生产的趋势,要求机器人末端执行器能适应各种场合。随着生活水平及医疗水平的提高,机器作为一种医疗辅助器械更应该以高度的柔顺性和环境适应性来辅助医疗。为解决传统刚性执行器存在的硬度大、结构笨重、环境适应性差及安全系数较低等问题,研究者对软体驱动器进行了研究。
人们受自然界中的生物如象鼻、章鱼臂、海星等的启发[3],对软体驱动器的结构进行设计,使得软体驱动器能够实现大的变形,从而完成对物体的抓取等动作。
南京理工大学的郭钟华[4]等参照国内外前人对软体驱动器的研究,研究出一款气动驱动的柔性夹持器[5-6];为解决驱动器开口较小的问题,林浩鹏在柔性夹持器的基础上研究出一款气动软体塑形夹持器[7];上海交通大学的谷国迎团队设计了基于纤维增强型驱动器的气动软体抓手[8];北京航空航天大学的王田苗等设计了一款可控三维运动的软体驱动器[9],此外,他们还设计了一款可变长度的软体仿生夹具[10];广东工业大学的管贻生[11]等从尺蠖的足部钩爪中获得灵感,仿尺蠖钩爪的钩爪式柔性夹持器,可用于危险探测及农业采摘等;立命馆大学设计了一款预应力软夹持器[12-13],解决了午餐盒包装的抓取问题。
虽然国内外学者在对软体驱动器的设计研究方面进展很多,但是如何对其建立有效的模型并采用合适的分析方法,到目前为止仍是一个极具挑战性的问题。
绝对节点坐标法[14](ANCF)是Shabana 提出的一种有限元分析方法,它基于一般连续介质力学,将传统有限元中的转角坐标替换成梯度向量,只使用一个坐标系,减少了坐标转换之间存在的误差,且单元质量阵为常数阵,不存在离心力和科氏力,因此更适用于大变形、大转动问题。到目前为止,研究人员已经对ANCF 梁单元、板单元及实体单元进行了研究[15],由于本文研究的多腔体气动软体驱动器为三维模型,其构型较为特殊,本文采用ANCF 四面体单元[16]进行分析。气动软体驱动器一般由橡胶等超弹性材料制成,为非线性不可压缩材料。Maqueda[17]等基于ANCF 梁单元,构建了Neo-Hookean 和Mooney-Rivlin 非线性本构模型;Jung[18]等研究了Neo-Hookean、Mooney-Rivlin 和Yeoh 本构模型下的悬臂梁受弹性力作用下的瞬态响应,得到Yeoh本构模型下的结果较其他两个本构模型的结果与实验误差最小,因此本文使用基于Yeoh 本构模型的ANCF 四面体单元对气动软体驱动器进行建模分析。
1 基于ANCF 方法的Yeoh 四面体单元
本文采用基于Yeoh 本构的三维四面体单元对气动软体驱动器进行建模,四面体单元模型如图1 所示。图1 中,oxy 为笛卡尔坐标系,与全局参照系相关联。ξ,η,χ,ζ为体积坐标,单元任意点P 的位置坐标可以表示为
式中:S——形函数;x,y,z——笛卡尔坐标下P 点的坐标;ξ,η,ζ,χ——体积坐标系下的P点坐标;p——笛卡尔坐标系下的节点位置矢量;e——体积坐标系下的节点位置矢量;T——笛卡尔坐标节点位置矢量与体积坐标节点位置矢量之间的转换矩阵,维度是48×48。
单元节点坐标可以定义为

形函数表示为

式中:I——3×3 的单位矩阵;ξ,η,ζ,χ——体积坐标。
1.1 基于Yeoh 模型的广义弹性力阵
超弹性材料弹性力的非线性本构模型一般采用应变能密度函数来描述。各向同性材料的应变能密度函数是张量不变量I1,I2,I3的函数,张量不变量I1,I2,I3可以定义为
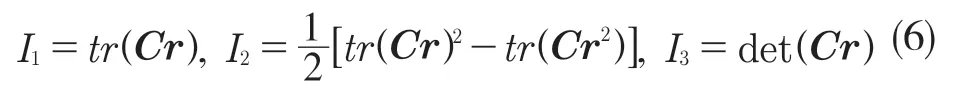
式中:Cr ——右柯西格林应变张量,Cr=JTJ,J——位置矢量梯度矩阵,,为保证不可压缩性,使得I3=1 或者J=|J|=1。因此应变能密度函数中只包含 I1,I2两项,可表示为

Yeoh 模型是基于应变能密度函数在第一个不变量I1的三项展开式中的表示,为

式中:C10,C20,C30——单轴拉伸实验测得的材料常数。
在本文中,利用罚函数法来确保不可压缩性条件。罚函数公式为

式中:α——不可压缩性常数,其值应足够大,以保证材料的不可压缩性。
因此,不可压缩弹性Yeoh 本构模型的应变能密度函数为
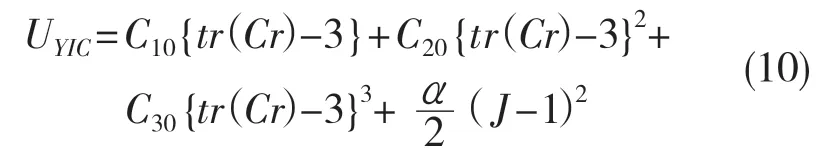
将式(9)对单元坐标p 求偏导可得

则弹性力阵可以表示为
单元弹性力阵的导数阵为QY对PT的偏导,表示为
1.2 单元压力矩阵
为了反映软体驱动器内部气腔的受力情况,首先需要求出作用于气动驱动器内部的压力阵。对气动驱动器施加压力所作的虚功为

式中:r——位移矢量,r=Se;S——形函数矩阵;ep——单元坐标列阵;p——压强;s——单元表面积;Qep——单元压力阵,表示为

1.3 单元平衡方程
在ANCF 中,本文研究的一端固定的多腔体气动软体驱动器静力学平衡方程可表示为

式中:K(e)——刚度矩阵;Qep——压力矩阵。
由于软体驱动器为超弹性材料制成,产生大变形,不易收敛,因此综合使用牛顿迭代法和载荷增量法对式(15)进行求解。
将式(15)改写为φ(e,λ)≡K(e)e-λQep,用λQep代替Qep,其中λ为载荷因子。将载荷因子分为M 个增量,总数为1,每个增量表示为Δλ=λm+1-λm,载荷增量表示为ΔQep=Qepm+1-Qepm=ΔλQep。
2 气动软体驱动器
本文针对如图2 所示多腔体气动驱动软体驱动器进行建模,制作过程详见文献[19],其尺寸如图3 和表1 所示。

表1 多腔体气动软体驱动器尺寸参数Tab.1 Dimensional parameters of multi-cavity pneumatic software driver
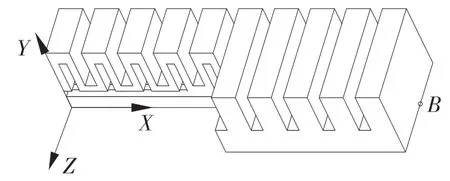
图2 多腔体气动软体驱动器Fig.2 Multi-cavity pneumatic software driver

图3 多腔体气动软体驱动器尺寸Fig.3 Size of multi-cavity pneumatic software driver
3 超弹性气动软体驱动器力学分析
在只考虑受压的情况下,本文对超弹性气动软体驱动器进行力学分析。本算例所用气动软体驱动器尺寸如表1 所示,材料参数如下:C10=0.373 MPa,C20=-0.037 MPa,C30=0.005 MPa,罚因子α=1 000 MPa。分别向驱动器内充入5,10,15 kPa 的压力,使用基于Yeoh 本构的绝对节点坐标四面体单元和基于Yeoh 的ABAQUS 四面体单元对该驱动器进行分析。
图4 为利用ABAQUS 分析时划分9 192 个单元,5,10,15 kPa 下软驱动器的变形情况。

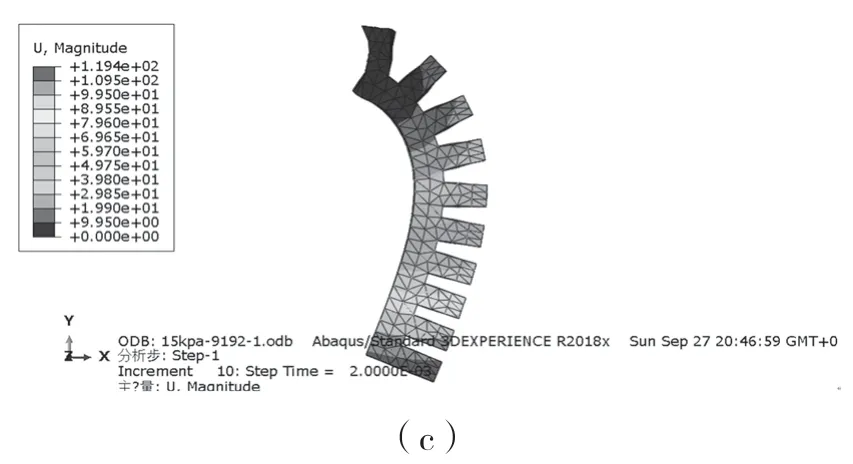
图4 ABAQUS 仿真结果Fig.4 ABAQUS simulation results
图5、图6 分别显示了气动软体驱动器末端B 点在ABAQUS 和ANCF 仿真下的位置情况。可以发现,无论是何种方法进行仿真,在一定范围内压力越大变形越大。

图5 ABAQUS 仿真B 点位置随压力的变化Fig.5 ABAQUS simulates the change of point B position with pressure

图6 ANCF 仿真B 点位置随压力的变化Fig.6 ANCF simulates the change of point B position with pressure
图7—图9 分别显示了不同压力情况下驱动器末端B 点X 方向和Y 方向的位置随单元数增加的变化情况。从图中可以看出,随着单元数的增加,B 点X 方向位置与Y 方向位置在ABAQUS和ANCF 仿真下的结果趋于一致,验证了基于ANCF 的气动驱动器建模的有效性。

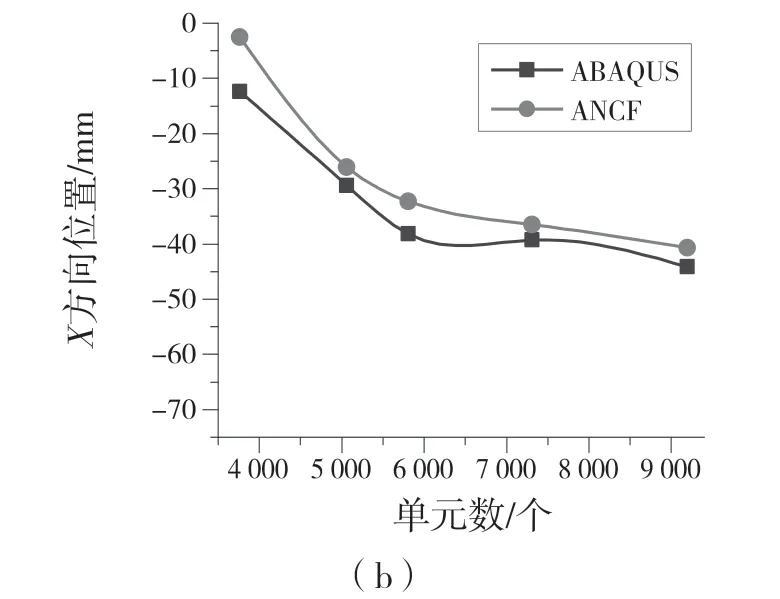
图7 5 kPa 下B 点的位置Fig.7 The position of point B when pressure is 5 kPa
4 结论
基于Yeoh 本构模型的ANCF 四面体单元对多腔体气动软体驱动器进行了建模。基于Yeoh本构模型的应变能密度函数推导了ANCF 四面体单元弹性力阵及其导数阵。对受压力情况下的多腔体气动软体驱动器进行数值仿真,得到以下结论:
(1)随着单元数的增加,ANCF 仿真结果与ABAQUS 仿真结果逐渐趋于一致,验证了基于ANCF的气动软体驱动器建模的有效性和收敛性。
(2)不管是ANCF 仿真还是ABAQUS 仿真,随着压力的增大,仿真结果逐渐趋于一个稳定的值。
文中基于ANCF 的多腔体气动软体驱动器模型是有效的,为绝对节点坐标法在软体机器人中的应用奠定了基础。然而,此类建模中对驱动器划分的单元数较多,对平衡方程的求解提出了更高的要求,为了实现高效的求解,对适合超弹性材料的高效求解算法提出了更高的需求。
——三角形一个共线点命题的空间移植

