多翼离心风机的气动噪声预测与降噪
邓伟,苗晓丹
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
多翼离心风机作为一种应用广泛的叶轮机械,在家用电器领域如空调、换气扇、风冷冰箱等发挥重要作用,给人们生活带来便利。离心风机内部复杂的流动变化致使流场压力脉动而产生的气动噪声给人们的产品体验以及身心健康都会造成很大的影响。按照GB 19606-2004《家用和类似用途电器噪声限值》规定,空调噪声限值为40~68 dB,该噪声限值为旋转噪声与气动噪声低频段的叠加值。噪声指标成为行业焦点,这也使得降噪成为当前风机研究的热点与难题。目前,国内外研究学者着力于从仿真模型与方法的改善,蜗壳、叶轮等结构参数的改进方面来实现离心风机降噪。王惠茹[1]等人以某发动机风扇为研究对象,运用Fluent 计算稳态压力场,将其作为边界条件导入到LMS Virtual Lab 中,利用Acoustic 模块计算其气动噪声。动静交界面采用滑移网格的方法处理,将壁面流体区定义为动的区域。湍流模型选用了LES 模型,将稳定的压力场作为声学仿真的边界条件,得到噪声仿真结果,并在一个半消音环境下进行了试验验证,噪声误差均在4%以内,验证了联合仿真的准确性,但仿真运行所占内存空间很大,对处理器要求很高;方开翔[2]等人对风机内部流场进行数值模拟以及噪声预测。稳态流场模拟的湍流模型采用RNG k-ε模型,动静交界面采用MRF 移动参考坐标系模型,瞬态流场的湍流模型采用LES 大涡模拟,用滑移网格求解动静交界面。通过叶片穿孔降低气流紊流强度达到降噪,穿孔角度为45°,穿孔系数为0.08 时风机正前方1 m 处声压级降低8.23 dB,但穿孔对风机性能如流量、效率等有较大影响;刘晓良[3]等人采用基于离心风机内部非定常流场的气动声源数值计算分析方法,结合试验测量,研究了改变蜗壳宽度对前向离心风机气动噪声和气动性能的影响。采用滑移网格方法处理动静交界面。其中,非定常计算控制方程采用三维雷诺守恒N-S 方程,湍流模型采用Realizable k-ε模型,近壁面选择标准壁面函数。研究结果表明,风机的全压和效率随着蜗壳宽度的增加而提高且蜗壳宽度增量为15 mm 时,噪声在大流量区域噪声有所减弱,但未定量分析噪声。当前的研究在数值模拟方法上进一步完善,定性分析了结构参数对风机流场与噪声的影响,未进行定量分析。在这些研究的基础上,本文用数值模拟的方法研究叶片数目、叶轮与蜗舌间距、蜗舌形状、蜗壳出风口长度等结构参数对离心风机气动噪声的影响,对所选取的多翼离心风机进行参数化建模,以达到风机噪声预测与降噪的目的。
1 计算模型
离心风机主要分为4 部分:进口、叶轮、蜗壳和出口,入口段、出口段和蜗壳为静止部件,叶轮为转动部件。考虑到多翼离心风机的叶轮结构较为复杂,且对流场仿真的干扰作用,可以忽略不计,因此在保证模型计算准确性的前提下对风机结构进行简化建模。多翼离心风机的三维模型如图1 所示,风机叶轮三维结构如图2 所示。原型离心风机的叶轮外径为157 mm,内径127 mm,叶片数为46,叶片高度为85 mm,厚度为1.35 mm。设置的工作转速为1 000 r/m。

图1 离心风机三维结构示意图Fig.1 Three-dimensional structure sketch map of centrifugal fan

图2 叶轮结构示意图Fig.2 Structural sketch of impeller
2 数值模拟理论
流体在风机内的流动在绝大多数情况下都为湍流状态[4],故风机内的流动要遵守湍流方程。对于本文计算的多翼离心风机模型,由于不考虑传热等方面的问题,因而在计算时可以不需要考虑能量方程。对这些物理定律的数学表达形式即为流体力学上的控制方程。
连续性方程

表述的是三维可压流体的连续性方程,ρ表示流体密度,由于本文研究的对象为多翼离心风机,流体的速度不是很大,一般可当作不可压缩流体来计算,因此ρ为定常数。因此,标准方程(1)可简化为

动量方程
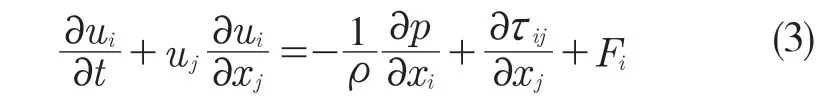
式中:p——静压;ui,uj——流动速度分量;Fi——质量力;τij——应力张量分量,定义为
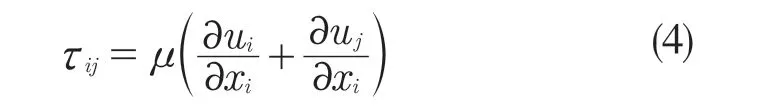
Lighthill 方程
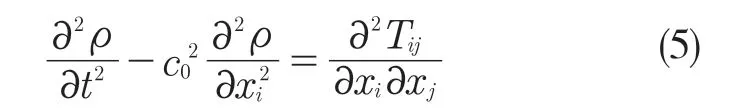
式中:Tij——Lighthill 应力张量,即

这时,我会想,母亲每次骂完我,心里也会疼的吧?慢慢地,当年对她的那些恨和不满,越来越淡。我开始三天两头就回娘家看看她,我好像习惯了她训我,然而,她骂我却骂得越来越少,反过来,我开始经常数落她了。我怪她光会省钱,怪她操心太多,怪她不懂得照顾自己……
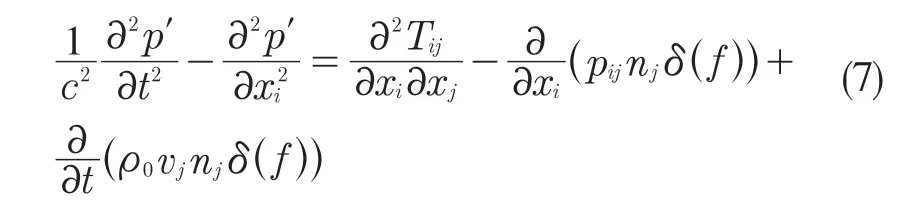
式中:右边第1 项——四极子声源,描述了湍流引起的四极子噪声;第2 项——偶极子声源,描述固体壁面压力脉动引起的偶极子声源;第3项——单极子噪声。由于多翼离心风机的噪声主要由非定常流场引起的压力脉动产生[5],因此本文以偶极子声源作为分析研究的对象。
3 数值计算分析
3.1 网格划分
如图3 所示为划分网格后的模型图,包括进出口区域、叶轮区域、蜗壳区域,各个计算域之间用interface(交界面)进行连接。对叶轮、蜗壳等复杂区域采用非结构化网格[6],相较于结构化网格,其自适应性更好,仿真结果更贴合实际情况。声源区域主要为叶轮区域,根据计算频段为10 kHz 以下的声源条件,得出最大网格尺寸为3.4 mm。对叶轮、蜗壳网格加密处理,使划分后最大网格为2 mm。经过网格无关性验证后,叶轮区域的网格数约为35 万,总网格数约为50 万。风机运行时整体是无移动的状态,因此所有边界条件设置为wall 的壁面类型均为无滑移,叶轮区域设置为旋转区域(moving wall),转速为1 000 r/m。设置进口压力为101 325 Pa,出口压力为101 325 Pa,即进出口绝对压力值与大气压相同。控制方程为N-S 方程,定常计算采用SIMPLE 算法,湍流模型为RNG k-ε,梯度求解选择Green-Gauss Cell Based。动量方程、湍流耗散方程均使用二阶迎风离散格式。非定常计算的湍流模型为LES 大涡模型,多CPU 并行计算,计算时间步长Δt=5×10-6s。求解时收敛残差设定为1e-4。

图3 网格划分Fig.3 Gridding
3.2 流场特性
离心风机定常计算采用的湍流模型为RNG k-ε,该模型能模拟分离流、二次流、旋流等复杂流动[7]。离心风机的非定常流场存在较强的逆压梯度,且蜗壳流动通道和叶轮旋转的非周期性组合,使其直接求解比较复杂,所以采用合适的湍流模型是预测多翼离心风机气动噪声的关键。本文非定常计算选用大涡模拟,取标准壁面函数、压力入口、压力出口。大涡模拟(简称LES)通过某种滤波函数将大尺度的涡和小尺度的涡分离开[8],大尺度的涡直接模拟,小尺度的涡用近似模型来封闭。LES 流动条件便于控制[9],计算结果具有高精确度,并且能完整展现瞬态流场信息,逐渐被应用于流动计算中。
为了使瞬态流场的连续性残差收敛,本文先计算稳态流场,将其作为计算初值带入求解瞬态流场。定常计算时采用多参考坐标系MRF 模型处理动静交界面,非定常计算时采用滑移网格法处理动静交界面,具体流程如图4 所示。

图4 仿真流程图Fig.4 Simulation flow chart
原型风机稳态流场的速度矢量分布如图5 所示。流体速度在叶轮切向垂直于出风口处的分布呈梯级递减,且流域内速度最大值为34.46 m/s,出现在流体由叶轮至蜗壳出口切向而出的位置,说明流体在经叶轮加速,即将发生离心运动由出口流出时速度达到最大。由伯努利原理可知,此时该区域的静压最小,可判断出叶轮对风机流场静压分布有一定关联性。

图5 原型风机稳态流场速度矢量分布Fig.5 Velocity vector distribution of steady flow field in prototype fan

图6 原型风机稳态流场静压分布Fig.6 Static pressure distribution in steady flow field of prototype fan
图7 描述了风机内流场瞬态静压分布。蜗舌后部一小块区域压力明显高于周围,可判断蜗舌对流场有干涉作用。叶轮靠近蜗舌的区域出现一局部压力明显小于周围的区域分布,判断该区域气流运动不规则,出现回流、紊流的状况,因此改善该区域的流动状况,对风机整体性能的提升有重要作用。

图7 原型风机瞬态流场静压云图分布Fig.7 Distribution of static pressure nephogram in transient flow field of a prototype fan
针对上述流场仿真后处理结果云图,可得定性分析结果,即风机叶片数目、叶轮与蜗舌间距、蜗舌形状对风机内流场产生影响,从而作用于气动噪声。因此,实现离心风机降噪,可对多翼离心风机叶片数目、叶轮与蜗舌间距、蜗舌形状等参数进行优化。
图8 所示为流场最大速度与叶片数目之间的关系曲线。当叶片数为46 时,流场速度最大值和叶片数为42 的风机接近,为39 m/s,但风机提供的流量性能明显会比叶片数为42 的风机强。图9、图10 显示了流场最大及最小静压绝对值总和叶片数目呈现一定的线性关系,即最大静压随叶片数目的增加而减小,因此在选择叶片时综合考虑对流场最大速度及静压影响,选择叶片数目为46。

图8 流场最大速度与叶片数目关联曲线Fig.8 Correlation curve between maximum velocity of flow field and number of blades

图9 流场最小静压与叶片数目关联曲线Fig.9 Correlation curve of minimum static pressure of flow field and number of blades
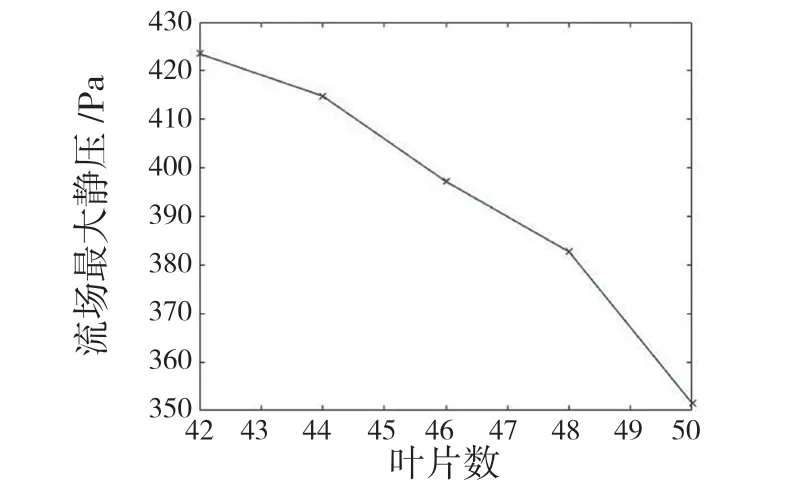
图10 流场最大静压与叶片数目关联曲线Fig.10 Correlation curve between maximum static pressure of flow field and number of blades
图11 为流场最大速度与叶轮相对蜗舌偏移距离的关联曲线。由图11 可知,相较于原型风机,偏移距离为-2~2 mm,流场最大速度变化不大,但当距离进一步增加或者减小时,流体速度呈现明显增强弱,说明一定程度上改变靠近蜗舌的空间大小并不能瞬时改善风机内流场的回流、紊流状况。
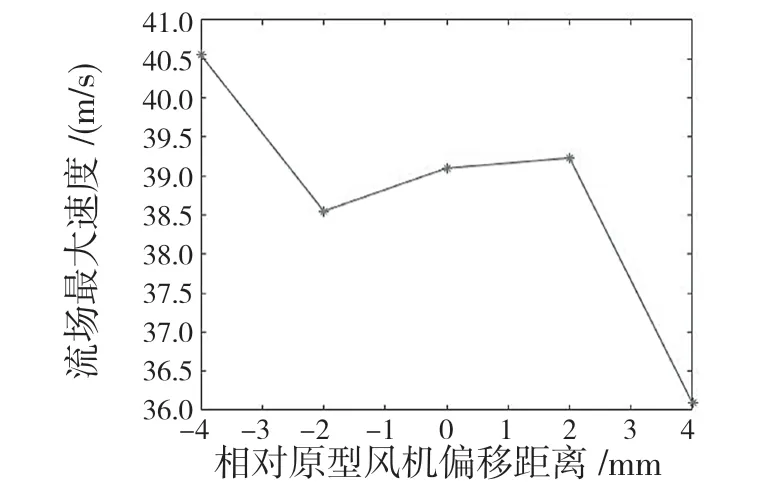
图11 流场最大速度与叶轮相对蜗舌偏移距离关联曲线Fig.11 Correlation curve between maximum velocity of flow field and distance between impeller and volute tongue
图12、图13 为流场最小静压及最大静压分布与叶轮相对蜗舌偏移距离的关联曲线。可以看出,静压与偏移距离的关联曲线大体趋势为递减关系,即当蜗舌与叶轮的间隔距离由小增大时,流场静压会逐渐减小,说明优化靠近蜗舌位置的蜗壳与叶轮之间的空间,可以改善流场的紊流现象,使得气体被均匀排出风机,因此选取相对原型风机偏移距离为-2 mm 进行优化。
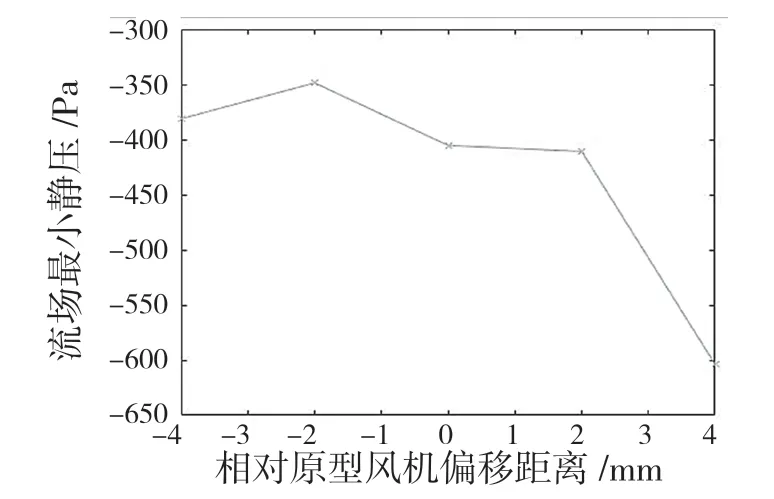
图12 流场最小静压与叶轮相对蜗舌偏移距离关联曲线Fig.12 Correlation curve between minimum static pressure of flow field and distance between impeller and volute tongue

图13 流场最大静压与叶轮相对蜗舌偏移距离关联曲线Fig.13 Correlation curve between maximum static pressure of flow field and distance between impeller and volute tongue
如图14 所示为流场最大静压与蜗舌半径的关联曲线。可知风机蜗舌半径为5 mm 时,叶轮最大静压最小,为385.2 Pa,说明该半径下的蜗舌优化了流场,流体。图15 为优化后的离心风机流场静压云图。在出风口及蜗舌附近,静压梯度均匀性显著提高,说明风机流场的气流运动不规则性得到改善,梯度范围更小。
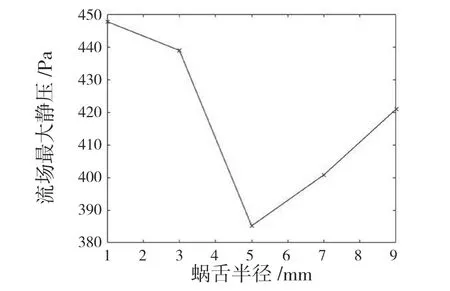
图14 流场最大静压与蜗舌半径关联曲线Fig.14 Correlation curve between maximum static pressure of flow field and volute tongue radius
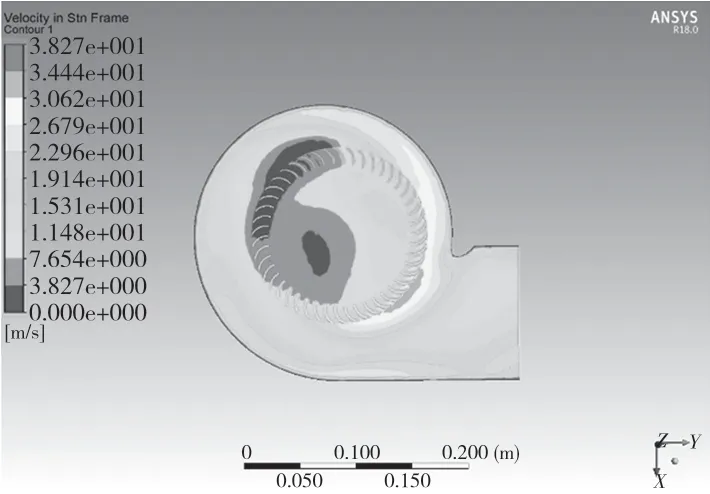
图15 优化模型流场静压分布云图Fig.15 Static pressure distribution nephogram of flow field for optimization model
3.3 声场特性
定常计算为非定常流场计算的残差收敛提供充分条件[10],有助于快速傅里叶求出噪声预测,且缩短非定常计算时间。在稳态流场计算的同时,利用宽频噪声模型可以求解出离心风机的噪声分布的大致区域及噪声声源特性,便于在使用FW-H 声类比模型预测远场噪声时选取合适的噪声监测点。ANSYS Fluent 的LES 湍流模型结合FW-H 噪声模型可在瞬态流动求解过程中同时执行噪声计算[11]。声压信号可以通过快速傅里叶变换得到,结合后处理获得全部声压标准和能量谱范围下的噪声数据图。如图16 所示为风机的声源特性,近场噪声分布区域。噪声源主要位于叶轮外表面,叶轮工作时与流体接触的交界面位置。

图16 风机全局声源特性Fig.16 Global sound source characteristics of fan
4 结论
叶片数目增加虽然在相同工况下获得的流量更大,但是加剧了偶极子声源的产生,使得低频噪声有明显升高。在噪声变化不明显的情况下,应选择叶片数目多的风机模型,增大流量,保证较好的离心风机性能。
叶轮与蜗舌之间的间隙聚集大量的回流、紊流,该区域的湍动能最大。为降低风机噪声,适当减小该间隙是可行的。但是该区域间隙过小易造成内部流体离心加速的不顺畅,进而引起流体聚集,同样会增大湍动能。
半径大的圆弧状蜗舌改善了离心风机出口气流,使得产生压力梯度的强度和范围更小,且分布更加均匀。
相较于原型离心风机,优化后的离心风机叶片数为46,叶轮与蜗舌间距较原型风机缩小2 mm,蜗舌半径为5 mm,由远场后处理结果得,风机能实现2 dB 的降噪。

