小学乘法运算的内容进阶及教材编写逻辑

刘加霞

北京教育学院初等教育学院院长，教育心理学博士，教授，教育部国培专家库成员;提出“把握数学本质是一切教学法的根”“实证研究学生是有效教学的根本”“培训实质是改变与创新”等观点，以及“CARE伙伴式”校本研修模式;在《课程·教材·教法》《中国教育学刊》《中小学管理》《人民教育》《小学数学教师》《小学教学》等期刊发表论文百余篇，著作有《小学数学有效教学》《小学数学有效学习评价》《小学数学课堂教学设计》等。

小学阶段运算的对象主要是自然数、分数与小数。各版本教材都是先编排自然数四则运算，不同的是分数、小数运算的编排顺序：有的先学习分数运算，再学习小数运算，有的则反之。内容编排的顺序不同，算法及解释其算理的依据就不同，乘法运算教学的整体逻辑结构也就不同。

近期，笔者看到关于多位数乘法、小数与分数乘法单元教学的几个案例，都特别强调“计数单位及其个数相乘”这一“原点”，有简单问题复杂化之嫌。因此，我们有必要追问：作为“高级运算”的乘法，其算法算理的教学应该退回“原点”，还是利用“前阶”内容通过推理获得？小学阶段所有乘法运算的内容进阶及逻辑结构是什么？“退回原点”追问算理是否符合整套教材的编写意图？

一、乘法算理是否要退回到“计数单位及其个数相乘”

有教师让学生以下述方式理解14×12的算法算理：“先拆后合”，即让学生通过“列表格”（拆分为“10+4”与“10+2”相乘）解释其乘积是2×4个“1”、2+4个“1×10=10”与1个“10×10=100”的和。这样理解是否有必要？根据乘法意义将之拆为“14×2与14×10”是否更清楚？又如，0.2×0.3有必要按“0.2×0.3=2×0.1×3×0.1=2×3×（0.1×0.1）=6×0.01=0.06”的步骤计算吗？分数乘法是否有必要这样计算：[3/5×2/7=][3×1/5×2×1/7=3×2×（1/5×1/7）][=6×1/35][=6/35]。

如此而言，2×3是否也得回归到“2×3=2×1×3×1=2×3×（1×1）=2×3×1=6”？那么，10×10=100、0.1×0.1=0.01、[1/5×1/7=1/35]等成立的理由又是什么呢？计数单位与计数单位相乘产生新计数单位的“算理”是否更让人难以理解？

如果按照前述逻辑，教材编排就要先学习计数单位与计数单位相乘;为了解释小数计数单位相乘，就要先学习分数乘法，再学习小数乘法;解释“分数单位乘分数单位”就需要通过分数的意义（借助分数面积模型图）求得结果。既然如此，我们为什么不直接借助分数的意义理解并归纳得到真分数乘真分数的计算法则呢？这不禁让我们思考：哪个知识点作为乘法运算的逻辑起点合适？借助已经学过的概念、性质与定律等，通过推理，概括乘法运算法则是否可行？

为此，笔者梳理了小学阶段自然数、分数与小数乘法运算的内容进阶及其逻辑结构，研究发现：大多数教材都没有退回运算的“原点”，而是以“前阶”内容作为教学乘法算法算理的起点。

二、自然数乘法教材编排顺序及对算法算理的处理

运算的学习内容包括运算的现实意义、算法算理以及运算性质、定律等。乘法的现实意义最丰富，有多种现实模型，能解决各类问题，其内容编排顺序为：二年级初步认识乘法，包括乘法的等量组聚集模型、实物或点子图矩形模型;三年级学习乘法的倍数模型、配对模型以及长方形面积的矩形模型;四年级学习乘法的“速度—时间”模型、“单价—数量”模型;五、六年级学习乘法的“工效—工时”模型以及正比例关系等。自然数乘法的内容都安排在二至四年级，其学习进阶及逻辑结构基本相同。

阶段1：二年级（上）“乘法口诀”。根据乘法意义探究发现“口诀”，通过口诀快速得到一位数乘一位数的积，其算理强调乘法意义——几个几的和，或者理解为以某个因数为“单位”，强调单位的个数，而不是回归到计数单位“一”“十”的个数。

阶段2：三年级（上）“一位数乘整十、整百、整千等数”。根据乘法意义，通过探究发现规律，得出口算法则——先转化为乘法口诀，再看因数中有几个“0”，积的末尾就添加几个“0”。有的教材将其安排为1课时内容，有的则与“两位数乘一位数不进位口算”合并作为1课时，但都没有强调必须学习10×10、100×100等算式。

阶段3：三年级（上）多位数乘一位数、0乘任何数。以“两位数乘一位数”的笔算为主，研究其算法算理，然后迁移至多位数乘一位数。不同版本教材的处理方式不同：有的只介绍竖式笔算并解释竖式中每一步的算理;有的则介绍多种算法，例如转化为加法计算、借助矩形点子图计算、转化为乘法口诀和整十数乘一位数计算，然后介绍乘法竖式。

阶段4：三年级（下）“因数末尾有0的口算乘法”。有的教材先研究一位数、两位数乘10的口算法则，再探究两个因数末尾都有0的乘法口算法则;有的教材通过探究几组“有特点”的乘法算式的规律，发现因数末尾有0的乘法口算法则。例如，计算3×2、3×20、30×20;12×4、12×40、120×40。所有版本教材都没有特别处理自然数计数单位乘计数单位的口算。

阶段5：三年级（下）“两位数乘两位数”。这个内容是笔算乘法的关键，不同版本教材的编写差异较大。有的教材直接介绍竖式算法，能够借助数的意义以及整十数乘两位数理解“第二个部分积”的算理即可。而有的教材与学习两位数乘一位数一样，介绍多种算法，并把“表格法”作为新知识学习。笔者更赞同前者的处理。要求学生将直观点子图、表格法以及竖式的每一步计算之间都建立相应联系的做法超出了课程标准的要求。

阶段6：四年级“三位数乘两位数”。课程标准只要求“能计算三位数乘两位数”，不要求计算其他更多位数的乘法。

可以看出，第1阶段、第2阶段是基础，第3阶段、第4阶段是关键，前4个阶段内容构成了乘法计算的核心，其他多位数相乘都是根据数的意义（组成与分解）以及乘法分配律转化为这4项内容。因此乘法计算的根本是口诀，该口算的口算，该笔算的笔算，能借助“前阶”内容解释“后阶”的算理即可，不需要也不適合追根到“计数单位及其个数相乘”。

三、分数、小数乘法教材编排顺序及对算法算理的处理

不同版本教材对于分数、小数乘法的编排顺序（学习进阶）不同。大陆各版本教材都是先学习小数乘法、再学习分数乘法，而台湾的翰林版、南一版教材则是先学习分数乘法、再学习小数乘法。台湾教材解释小数乘法的算法与算理是将小数乘法转化为分数乘法。

所有版本教材中分数乘法的内容进阶及其算法算理都相同：先学习“分数乘整数”（紧扣乘法意义、分数意义得到计算结果并归纳计算法则），再学习“分数乘分数”（根据分数意义，借助分数的“面积模型”得到分数乘分数的结果，并归纳计算法则）。没有任何版本教材用上文第一部分提到的方法计算分数乘分数。

不同版本教材对小数乘法算法算理的内容编排不完全相同，下面具体分析。

1.大陆教材小数乘法的内容编排及算法算理

人教版、北师大版、河北版等大多数教材都是按照小数乘整数、小数乘小数的顺序编排，其算法与算理也基本相同：①依据小数的现实意义将其转化为自然数（例如2.5元=25角），按照自然数乘法法则求积，再根据现实意义确定积的小数位数;②通过将小数乘10、100等转化为自然数，按照自然数乘法法则求积，再根据“积的变化规律”确定积的小数位数。在此基础上，归纳得到小数乘法法则：转化为自然数乘法进行计算后，再确定积的小数位数。

苏教版教材对于小数乘整数的处理方式略有不同，紧扣小数意义计算，例如2.35×3（列竖式计算）是235个0.01乘3，积是705个0.01，就是7.05。这与台湾教材对算法算理的处理相同。

2.台湾翰林版小数乘法的内容编排及算法算理

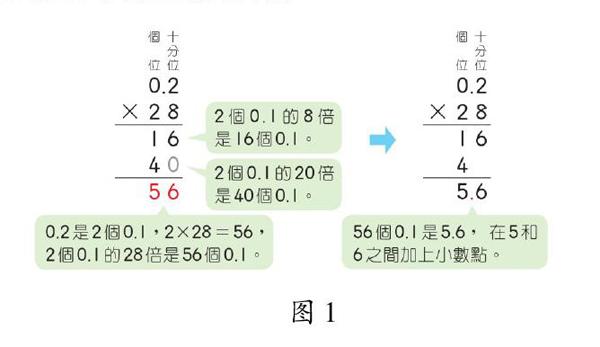
台湾翰林版教材仍然区分乘数、被乘数，因而小数乘法的编排较为“复杂”，其内容进阶分三个阶段。一是小数乘整数。四年级下学期学习一位小数、两位小数乘整数，五年级下学期学习三位小数乘整数。二是整数乘小数。五年级下学期学习整数乘一位、两位小数。三是小数乘小数。在五年级下学期学习，分为一位小数乘一位小数、两位小数乘一位小数、两位小数乘两位小数。

小数乘整数的算法算理是乘法的倍数含义和小数含义，如图1某例题所示。四年级没有总结小数乘整数的计算规律和法则，五年级下学期通过对比35×5和35×0.5的竖式计算过程总结：“整数乘以小数和整数乘法的算法很像，但要注意积的小数位数和乘数的小数位数相同。”

为了探究、归纳小数乘小数的运算法则，这版教材一共编排了6道例题和9道习题。无论几位小数相乘其算法算理都一样：首先转化为分数乘法计算得出结果，探究发现计算规律与法则，再通过练习验证与巩固计算法则。例如，教材引导学生将0.1×0.1、1.2×0.7分别转化成分母为十、百的分数乘分数计算后，让学生观察0.1×0.1=0.01和1.2×0.7=0.84两个算式，探究两个因数的小数位数与积的小数位数之间的关系（相同），再做3道类似的竖式计算题来检验和巩固这个发现。

3.对不同版本教材小数乘法编排逻辑的总结

小数乘整数、小数乘小数的算法算理主要有三类：根据小数的现实含义及乘法意义将小数乘法转化为整数乘法，再根据积的现实意义确定小数点的位置;根据小数意义及乘法意义将小数乘法转化为自然数乘法，再根据积的大小确定小数点的位置;利用“积的变化规律”将小数乘法转化为自然数乘法，再将积缩小相应倍数确定小数点的位置。

笔者所查阅的各版本教材，只有台湾南一版教材在解释小數乘小数算理时用到如“0.2×0.3=2×0.1×3×0.1=2×3×（0.1×0.1）=6×0.01=0.06”这样的方法，如图2所示。

笔者认为，教材内容的整体编排顺序决定着我们如何解释算理。该教材在竖式中用小数意义、小数计数单位乘小数计数单位来解释算理，学生很难理解。大陆各版本教材基本都是先学习“积的变化规律”，将小数乘法转化为自然数乘法再计算，学生对此比较容易理解。

既然乘除法是比加减法“更高级”的运算，我们就可以运用已经学过的数概念、运算性质和定律等，通过推理得出计算法则。是否“退回原点”解释道理、解决问题，我们应该辩证地看待。

责任编辑  刘佳