基于随机参数线性回归的交通流速度-密度关系模型研究
管星宇,潘义勇
(南京林业大学 汽车与交通工程学院,南京 210037)
0 引言
交通流基本图模型是交通流理论的基础,表征了交通流3个基本参数之间的关系:交通流量(辆/h)、速度(km/h)和密度(辆/km)。交通流速度-密度关系基本图模型包括确定基本图模型和随机基本图模型,对交通流基本图的深入挖掘有利于在交通状态识别、交通拥堵分析等领域发挥重要的作用[1-3]。
针对速度-密度关系确定基本图模型研究,Greenshields等[4]提出开创性的速度-密度线性模型,其缺点是在密度值较大或较小时,模型的效果变差。为了克服这个缺点,Greenberg对数模型[5]、Underwood指数模型[6]和Northwestern指数模型相继被提出[7],这些模型都是单阶段确定性模型。单阶段确定性模型采用最小二乘法进行参数拟合,对数据集的分布特征要求较高;模型采用一条曲线表征速度-密度关系,忽略了交通流异质性对速度-密度关系的影响[8]。
针对速度-密度关系随机基本图模型的研究,Muralidharan等[9]、Jabari等[10]和Fan等[11]分别针对Triangular模型、Newell模型和Aw-Rascle-Zhang(ARZ)模型推导出速度概率分布函数和密度关系模型,但是该方法只适用于特定模型,不能推广到其他交通流模型。Qu 等[12]提出基于不同分位点构建的交通流速度-密度关系基本图模型,既解决了模型的适用性问题,又能反映交通流异质性对速度-密度关系的影响,但是不能获得速度-密度关系的概率分布特征。
本文采用随机参数线性回归获得速度-密度关系随机基本图模型,随机参数线性回归在交通领域已经有了很多的应用[13-14],该方法通过获取变量系数的随机概率分布特征,反映出交通流异质性对交通流速度-密度关系的影响,这是本文研究的出发点。首先,基于随机参数线性回归建立交通流速度-密度关系随机基本图模型;其次,利用随机参数线性回归对实际交通流数据进行速度-密度关系进行参数拟合;再次,对随机参数进行假设检验和误差分析,并对结果进行数值分析;最后,总结了本文的研究成果以及进一步研究的方向。
1 随机参数速度-密度基本图
1.1 随机参数线性回归
随机参数线性回归是计量经济学中常见的数据分析方法[15],现已获得了广泛的应用,其基本的定义为:
yn=βn·xn+εn。
(1)
式中:yn、xn分别为连续型因变量和自变量数据;εn为服从正态分布N(0,σ2)误差项;βn为解释变量的随机系数,随着观测值的不同而变化,函数形式为:
(2)
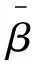
随机参数的求解是基于Halton序列模拟极大似然估计[13],Halton序列是一种为数值方法产生顶点的系列生成算法。
1.2 随机参数速度-密度基本图模型
将随机参数线性回归与传统确定性交通流模型相结合构建随机交通流速度-密度基本图模型,以Greenshields线性模型为例,所建立的随机交通流速度-密度模型可以表示为:
vn=an-bn·kn。
(3)
(4)
式中:n为观测数据索引值;an=(vf)n为随观测值随机变化的自由流速度;bn=(vf/kj)n为自由流速度与堵塞密度的比值,kn为第n个观测数据的交通流密度值。
非线性两参数模型的随机建模思想是通过对速度、密度数据进行相应的对数、幂指数变换,将非线性模型转换成线性模型进行参数求解。表1为基于随机参数线性回归的速度-密度关系随机基本图模型。

表1 随机参数交通流速度-密度基本图模型
2 数据来源与分析
TransGuide是德克萨斯州圣安东尼奥市的先进交通管理系统,是基于环形探测器和摄像机检测每20 s所有通过车辆的信息[16],包括车辆的速度、20 s的交通流量以及每辆车通过检测器的时间。通过TransGuide系统选取单向三车道I-10州际公路(中间车道,传感器识别号:L2-0010E-562.581)的非开源交通流数据进行分析。
(5)
k=ο/(l+d)。
(6)
通过对数据的筛选,获取3 256对速度-密度数据。表2为不同密度值对应的速度分布偏度(Skewness)系数值(Skewness=0表示对称分布,Skewness<0表示左偏分布,Skewness>0表示右偏分布),结果表明:k=5.03辆/km,速度服从正态分布;k∈[7, 38],对应速度服从左偏分布;k∈[40, 91],对应速度主要服从右偏分布。图1选取了3种不同的概率分布形式,随着密度值的增加,概率最高点的速度值呈现递减趋势,速度概率分布逐渐由右偏向左偏过渡。表2和图1的信息说明在实测的交通流数据中,由于交通流异质性的影响,不同密度值对应的速度是随机的,采用随机参数线性回归方法可以反映出速度-密度的随机特性。
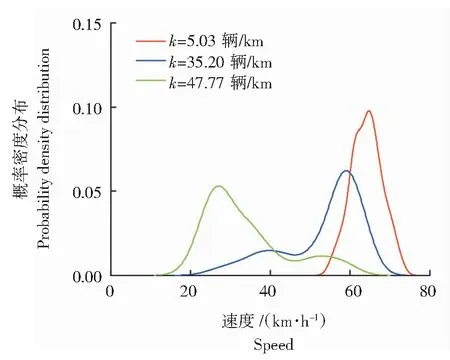
图1 不同密度下的速度分布图

表2 密度分布Skewness系数
3 数值实验
3.1 参数拟合
利用LIMDEP 11软件对表1中交通流速度-密度基本图模型进行固定/随机参数拟合。固定参数模型拟合使用最大似然估计法来求解参数值,随机参数模型通过模拟Halton序列最大似然估计法求解随机参数值[11],考虑计算时长和计算精度,Halton draws值设置为200。表3为固定/随机参数拟合结果,表3中a为常系数、b为自变量系数,4个模型的参数a、b含义与表1一致。随机参数线性回归假定选取的随机参数符合正态分布,并从3个角度进行数值实验:a随机-b固定、a固定-b随机、a随机-b随机。表3中小括号内数值表示随机参数的标准差,方括号内数值表示参数假设检验的P值,从表3中P值结果表明,固定/随机参数模型的拟合结果较好。表4为固定/随机参数模型的赤池信息准则值(AIC),AIC值越小说明模型的拟合优良性越好。
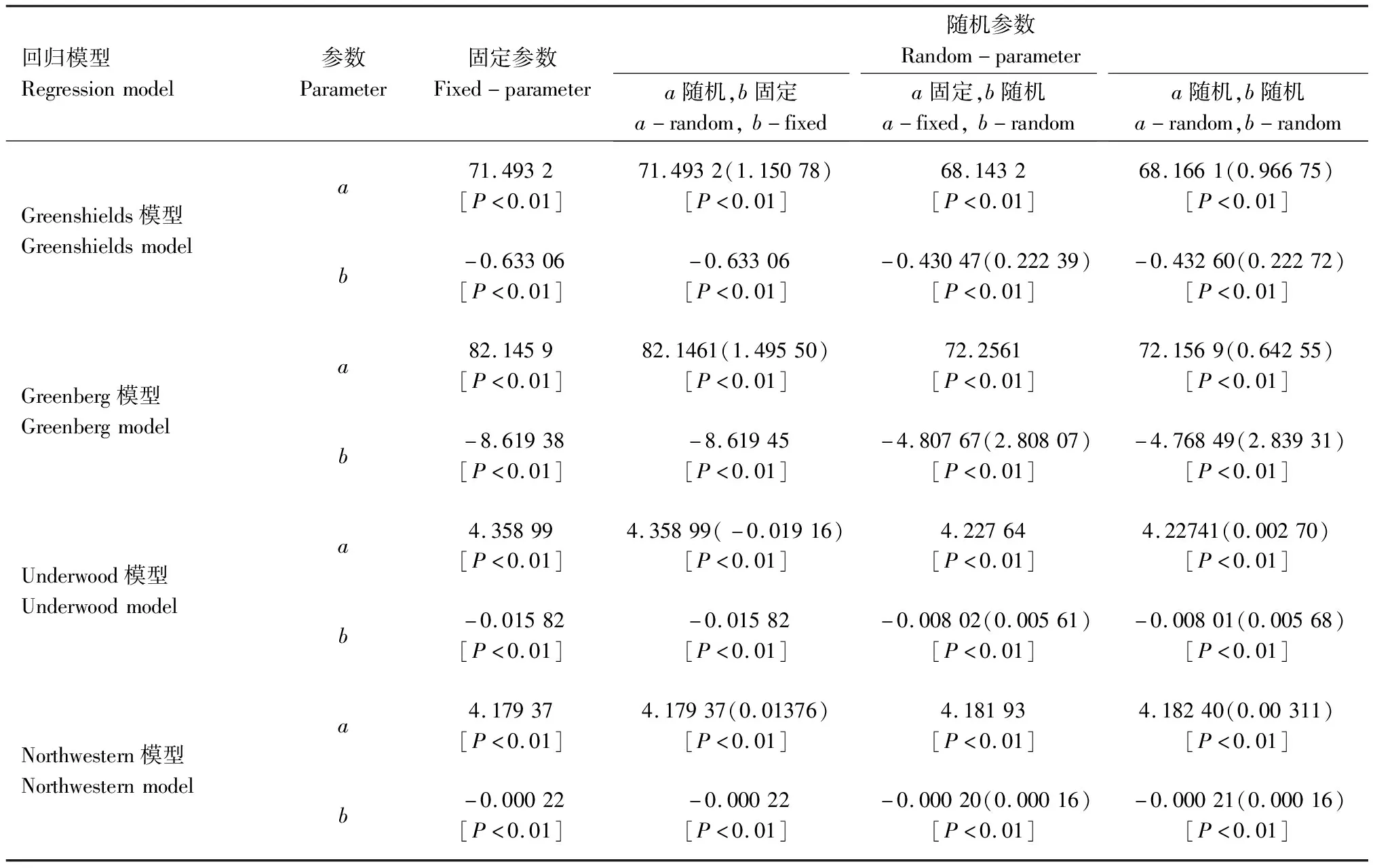
表3 固定/随机参数拟合结果
3.2 误差分析
对拟合得到4个随机参数交通流速度-密度基本图模型(a随机-b随机)进行平均绝对误差分析(MAE),图2—图5为随机参数模型的拟合值和实测值的散点图,图中红色圆点表示观测值散点图,蓝色圆点表示随机参数模型拟合值的散点图,绿色曲线表示固定参数拟合曲线图,FP_MAE表示固定参数得到的MAE值,RP_MAE表示随机参数得到的MAE值。
3.3 结果分析
(1)随机参数交通流速度-密度基本图模型较固定参数模型拟合效果好。从模型的拟合精度角度分析,表4的固定/随机参数模型AIC值揭示了2种现象:第一,与传统的固定参数回归模型AIC值相比,a固定-b随机、a随机-b随机所得到的随机参数回归模型AIC值较低,拟合精度较高;第二,a随机-b固定得到的AIC值比固定参数回归模型AIC值更高,拟合精度最低。从模型的误差角度分析,随机参数回归模型(a随机-b随机)的MAE值低于固定参数回归模型的MAE值,4个随机模型的MAE值分别降低了57.04%、81.30%、74.48%和52.27%,由图2—图5可以看出,与固定参数回归得到的确定性曲线不同,随机参数回归模型可以得到不同密度值下的随机速度分布,在密度值大于20辆/km时,随机参数模型的速度拟合值与真实观测值基本一致。

表4 固定/随机参数模型AIC值
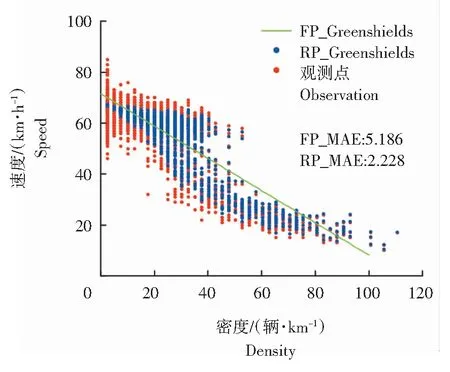
图2 随机Greenshields模型拟合值
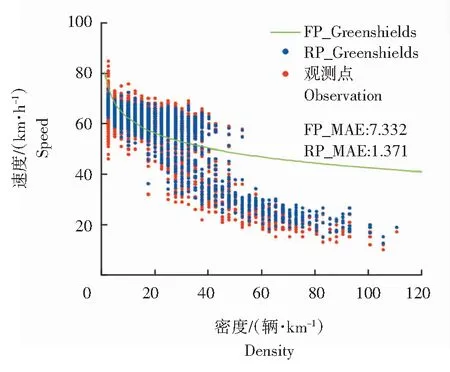
图3 随机Greenberg模型拟合值
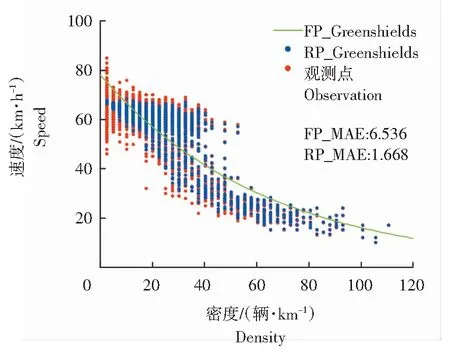
图4 随机Underwood模型拟合值
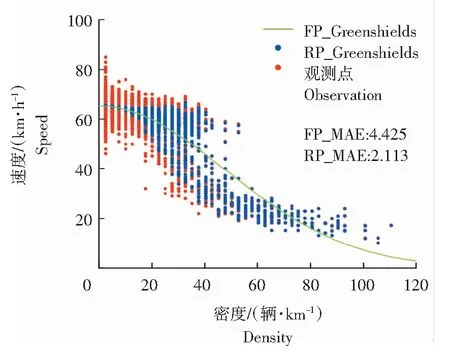
图5 随机Northwestern模型拟合值
(2)随机参数线性回归方法通过参数标准差反映交通流异质性对速度的影响,以Greenshields模型为例,表1中固定参数Greenshields模型表达式为:v=71.493 2-0.633 06·k,固定参数模型得到一条拟合曲线来表征I-10数据集的速度-密度变化特征,反映了不同密度的速度均值变化,无法体现出交通流异质性对交通流的影响。而随机参数模型将交通流中人、车、路和环境的异质性对交通流的影响用概率分布的形式体现出来,随机参数Greenshields模型常系数vf服从均值为68.166 1,标准差为0.966 75的正态分布,自由流速度有95%的概率落在66.271 3~70.060 9;变量系数vf/kj服从均值为-0.432 60,标准差为0.222 72的正态分布,说明97.395%的变量系数值为负值,速度随着密度的增大而降低,而2.605%的变量系数值为正值,表明在真实的交通流状态下,由于交通流异质性的影响,速度有2.605%的概率会随着密度的增大而增大。
(3)随机参数线性回归方法适用于不同的交通流速度-密度基本图模型,不同的随机参数交通流速度-密度基本图模型对数据的拟合效果也不同。从拟合结果分析,通过对模型进行线性转换,不同模型的常系数、变量系数结果完全不同,Underwood模型的常系数服从均值为4.227 41,标准差为0.002 70的正态分布,Northwestern模型的常系数服从均值为4.182 40,标准差为0.003 11的正态分布,相较于Underword模型,Northwestem模型对密度进行平方化处理后,得到的自由流速度降低,但是自由流速度变化的范围增大。从拟合散点图来分析,不同的模型得到了不同的速度拟合值,在密度值较高时,4个模型都表现出了良好的拟合精度,而受到模型自身特点的影响,4个模型在低密度状态下表现出了不同的速度变化特点,Greenberg模型对密度进行了对数化处理,因此在低密度情况下,速度与密度对数化后的分布较为离散,低密度下得到的速度分布较为分散,比较贴近真实的数据分布;Northwestern模型在数据进行转换后,低密度下的数据较为密集,因此其低密度下的速度值变化接近一条直线;而Underwood模型的数据经过转换后的分布与Greenshields模型类似,因此,两者之间随机参数拟合得到的散点图最为相似。
4 结论
针对交通流速度-密度关系基本图问题,引入随机参数线性回归建立随机交通流速度-密度关系基本图模型,数值实验获取随机模型参数的概率分布函数,并进行了参数检验和误差分析,数值实验结果表明:与固定参数交通流速度-密度关系基本图模型相比,随机参数交通流速度-密度基本图模型考虑了影响交通流的异质性因素,反映出交通流异质性对交通流速度-密度关系的影响;提出的方法为交通流基本图随机模型构建了一个方法论,可以与不同的交通流速度-密度关系基本图模型相结合;随机参数模型MAE值较低,拟合结果贴近于真实数据,可以考虑将随机模型运用于交通流的建模和仿真中,提高仿真的维度和灵活性。本文提出的模型获取的自由流速度变化范围较小,无法反映低密度状态异质性对交通流速度-密度关系的影响,进一步研究需要考虑数据不同分位区段的随机交通流速度-密度关系分布特征。

