基于寒区混凝土连续箱梁长期监测数据的温度场试验分析

谢凯，孙全胜，胡丹丹，刁万民

(东北林业大学 土木工程学院，哈尔滨 150040；黑龙江省公路建设中心，哈尔滨 150081)

0 引言

运营期间的混凝土桥梁暴露在自然环境中会受到日照升温和日落降温以及骤然降温的长期影响，在此期间桥梁在受到日照辐射后，会因为混凝土较差的导热性，混凝土内部温度和外部温度产生一定的延迟，从而混凝土结构内外会产生较大的温差[1]。在温差作用下，纵向纤维约束以及超静定结构体系的多余约束的制约会导致混凝土箱梁产生温差应力[2]。因此，桥梁处于服役期间，不仅受到车辆荷载等其他外部荷载的不利影响，还会受到由于温度变化引起的温差应力的影响[3]，在桥梁结构中，这种温度荷载产生的应力，甚至会超过车辆荷载产生的应力[4]。

国内外众多学者对桥梁的温度场作用已经进行了深入的研究[5-10]，如：叶见曙等[11]对南京长江第二大桥北汊桥进行了温度观测，研究了混凝土箱梁的温度场分布特性，并提出了适用于该地区的温度梯度模式；肖建庄等[12]用概率统计学的方法分析了气象参数的分布规律，计算了其代表值，并分析了混凝土箱梁的温度场；顾斌等[13]以苏通大桥辅助航道桥为例，建立了以气象数据为基础的桥梁有限元模型，并用统计学的手法计算了在五十年一遇标准值的条件下桥梁的温度场；刘逸平等[14]对华南地区的一座混凝土连续梁桥进行了长期的温度数据采集，并在数理统计的基础上对华南地区混凝土连续梁的温度分布特性进行了分析，得出该桥的温度分布规律；丁幼亮等[15]在珠江黄埔大桥北汊斜拉桥和南汊悬索桥上建立了健康监测系统，在此基础上进行了一年的温度数据采集，建立了2个桥的温差数学统计模型，并求得了温差标准值；陈一飞等[16]对沧口道桥进行了温度监测，分析了年温差变化规律，对主要测点进行了概率密度分布拟合，并以监测数据为样本计算了温差基准值。

我国不同的地区日照辐射存在很大的差异，产生的温度荷载也有所不同[17-19]。然而，对于我国寒冷地区的混凝土桥温度分布的研究还是很少。本文基于齐齐哈尔某座运营期的混凝土连续梁桥健康监测系统，将通过建立统计学模型的方法对寒区混凝土箱梁的温度分布规律进行研究。

1 工程概况

1.1 工程背景

该桥结构形式为连续混凝土箱梁，位于齐齐哈尔市境内，于1995年9月竣工。齐齐哈尔位于我国北部的嫩江平原，冬季寒冷漫长，夏季炎热短促，属于寒温带大陆性季风气候。一年中最高温度月份为7月份，最高可达到35.6 ℃，一年中最低温度为1月份，最低可达到-38.6 ℃。其中7月份平均气温为22.4 ℃，1月份平均气温为-21.38 ℃。齐齐哈尔年降雨量为500 mm，其中夏季降雨量可达到年降雨量的80%以上。因此，为了掌握当地混凝土箱梁结构内部不同位置的受力和温度情况，对该桥安装了健康监测系统来记录不同时刻主要截面的温度。

桥梁一方通往齐齐哈尔，一方通往满洲里。桥长1 056.88 m，主桥全宽17.5 m，本论文对主桥连续梁桥进行分析，其桥面横向布置为：1.25 m人行道、15.0 m行车道、1.25m人行道。

另外，该主桥为跨径布置60 m+3×100 m+60 m的预应力混凝土单箱单室变截面连续箱梁，如图1所示。

图1 总体布置图

该桥上部结构为5跨预应力混凝土连续箱梁桥，主梁采用单箱单室变截面箱梁,箱梁根部高度为6.0 m，跨中高度3.0 m，边跨支点2.4 m。该箱梁全宽为16.5 m，翼缘板长4.25 m，底板宽8.0 m。

箱梁的顶板厚度分别为0.30 m和0.40 m，底板厚度为0.30～0.80 m，腹板厚度分别为0.46、0.56、0.68 m。如图2和图3所示。

图2 主梁墩顶截面(单位:cm)

图3 主梁跨中截面(单位:cm)

1.2 测点布置及监测仪器

该桥的温度传感器安装在主梁的跨中截面，测量时间间隔为30 min,因此每个传感器一天共测得48组数据。整个健康监测系统于2020年1月正式运行，本文选取2020年1月至2021年1月为期1 a的监测数据进行分析，研究截面选择11#跨的跨中截面，传感器布置情况如图4所示，温度监测系统现场照片如图5—图7所示。

图4 传感器布置图

图5 温度传感器现场照片

图6 数据采集模块现场照片

图7 无线传输模块现场照片

2 箱梁温度监测数据分析

2.1 箱梁温度分布特征

将采集一年的温度监测数据进行粗差剔除，各测点温度极值见表1，绘制出11#跨的跨中截面上的各测点温度变化曲线如图8所示。

从表1可知，由于几何对称性，左右腹板的最低温度极值以及最高温度极值相差不大，顶板和底板最低温度相近而最高温度极值最大可相差3.8 ℃。其中，表1中Max代表最高温度极值，Min代表最低温度极值，R代表最高温度极值与最低温度极值之差。

表1 各测点温度统计表

由图8可知，混凝土箱梁横截面各点具有相似的温度变化规律，都具有典型的季节变化性，随着时间由冬季向夏季推移温度呈递增趋势。对比图8(c)和图8(d)可以看出腹板上沿横截面中轴线对称的测点温度变化曲线相似，同时箱梁具有几何对称性，因此可取箱梁右半部分进行分析。

2.2 箱梁温差分布特征

自然环境中的温度荷载作用在运营期的桥梁上会使其产生一定的变形和应力，进而使桥梁的稳定性受到损害[11]，因此接下来将对该寒区混凝土箱梁桥的竖向温差和横向温差进行统计分析。

由图9可得，箱梁同一截面的不同测点的温差存在季节变化性，随着日照温度的增加温差增大，整体趋势和图8温度变化曲线相近，在1月份温差较小，到6月份温差增大,到12月份逐渐减小。

图8 测点温度变化图

图9 不同测点温差变化图

由表2可知，顶板的T2-1与T2-3最大正负温差值相近，正负温差占比也相似，再一次验证了箱梁温度分布的对称性。同时T2-10的最大温差为7.6 ℃，T5-12的最大温差为8.5 ℃，由此可见顶板和底板都分别存在一定的横向温差。T2-5最大温差可到达4.7 ℃，T10-12最大温差可到达6.8 ℃，可见顶板和底板间存在着一定的竖向温差。

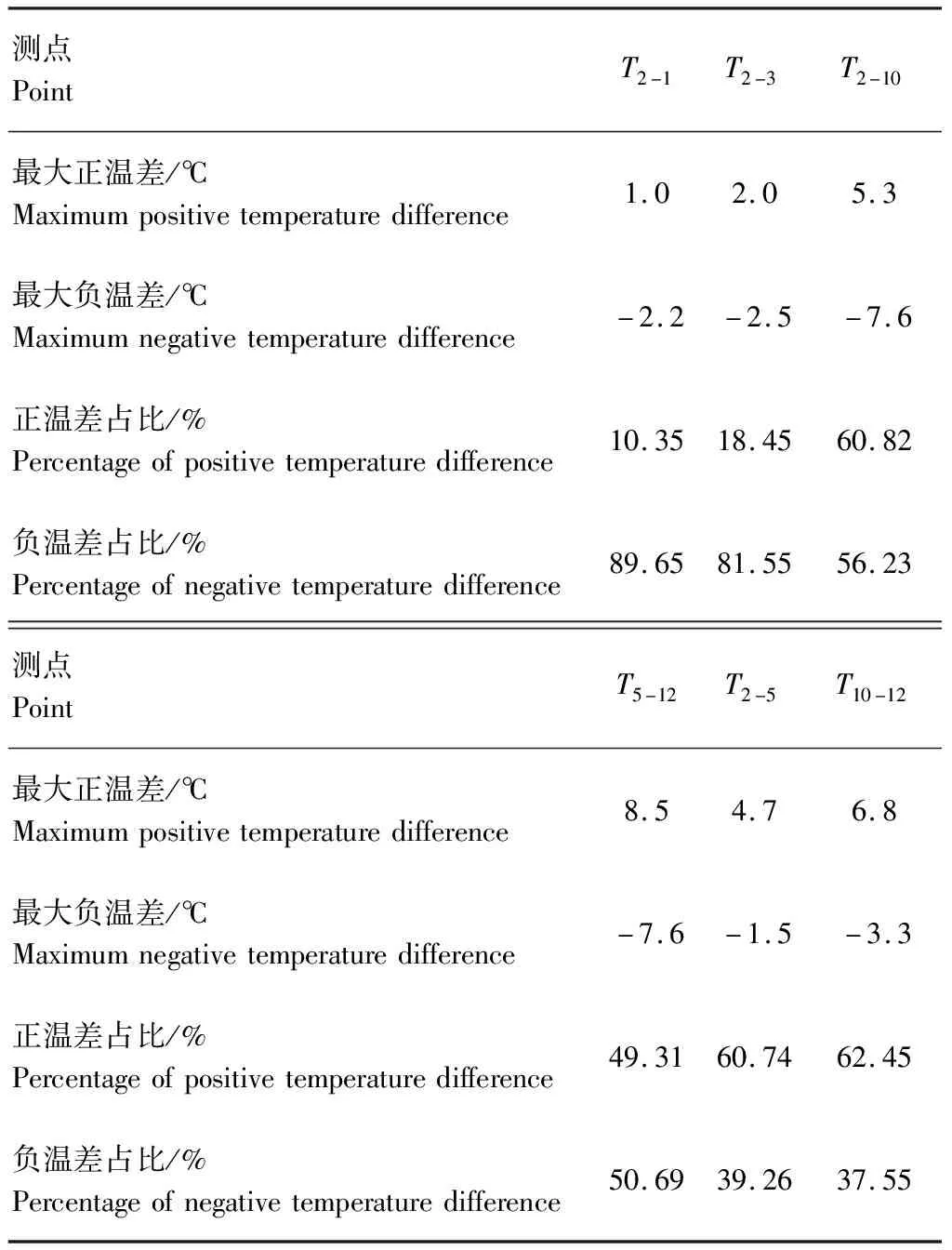
表2 各测点温差统计表

3 箱梁温差拟合

由测点数据看出，随时间变化，同一截面的不同测点间的温差变化趋势是一个平稳随机的过程，因此可以根据平稳随机过程的遍历性定理，将温差作为随机变量，从而对应测点温差的概率密度分布函数采用统计学中的非线性最小二乘拟合、显著性检验等方法获得。由于正温差和负温差在箱梁结构中产生不同的温度应力，因此做温差分布分析时应该分正温差和负温差去进行研究。

在多个模型的拟合对比下，选用公式(1)来描述寒区混凝土箱梁正负温差的概率密度统计模型。

f(T)=αW(a1,b1)+βW(a2,b2)

(1)

式中：f(T)为寒区混凝土箱梁同一截面各测点之间温差Ti-j的概率密度分布函数，由2个Weibull(Weibull分布又称韦伯分布，是连续性的概率分布，是可靠性分析和寿命检验的理论基础)分布的加权和组成，其表示为W(a,b)；该函数表达式的控制参数由a和b来表示；2个W(a,b)的权重分别为α和β，且α+β=1；T指的是温差Ti-j；e为自然常数，e≈2.71828。

3.1 横向正温差拟合结果

图10是分别对该寒区混凝土箱梁的顶板与底板的横向正温差T+2-10和T+5-12以及横向负温差T-2-10和T-5-12进行非线性拟合情况。拟合曲线均通过显著性水平为0.05的Pearson检验，温差概率密度分布函数的参数估计值见表3。

表3 横向温差概率分布函数参数

由图10可以看出，寒区混凝土箱梁横向温差的概率密度数据拟合程度较好，可以准确反映桥梁的横向温差概率密度统计特性。

图10 测点温差概率密度分布图及拟合曲线

3.2 竖向正温差拟合结果

表4 竖向温差概率分布函数参数

从图11可以看出，寒区混凝土箱梁横向温差的概率密度数据拟合程度较好，可以准确反映桥梁的竖向温差概率密度统计特性。

图11 测点温差概率密度分布图及拟合曲线

4 结论

用统计学的方法对该寒区混凝土箱梁桥一年的温度监测数据进行了分析，得出以下结论。

(1)寒区混凝土箱梁桥具有明显的季节变化性，冬季最低温度为-18.7 ℃，夏季最高温度为34.8 ℃，随着时间推移，温度先升高后降低，同时温度变化具有几何对称性。

(2)寒区混凝土箱梁桥同一截面的不同测点的温差存在季节变化性，随着日照温度的增加温差增大。

(3)寒区混凝土箱梁桥正负温差概率密度分布特性服从2个Weibull分布的加权和，不同测点间温差概率密度分布函数的控制参数不同。