最短路径怎么找

朱华平

[真题呈现]

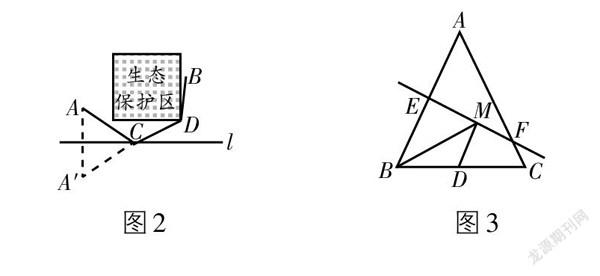
例1（2020·江苏·南京）如圖1①，要在一条笔直的路边[l]上建一个燃气站，向[l]同侧的[A]，[B]两个城镇分别铺设管道输送燃气. 试确定燃气站的位置，使铺设管道的路线最短.

（1）如图1②，作出点[A]关于[l]的对称点[A]'，线段[A'B]与直线[l]的交点[C]的位置即为所求，即在点[C]处建燃气站，所得路线[A—C—B]是最短的. 为了证明点[C]的位置即为所求，不妨在直线[l]上另外任取一点[C']，连接[AC']，[BC']，证明[AC+CB<AC′+C'B]. 请完成此证明.

（2）如果在[A]，[B]两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域. 请给出生态保护区是正方形区域且位置如图1③所示情形下铺设管道的方案（不需说明理由）.

[破解策略]

解决最短路径问题，关键是通过作A，B中的一个点关于直线l的对称点，将直线同侧的两点转化为直线异侧的两点，再运用“两点之间，线段最短”来确定最短路径. 因此，解决最短路径问题，常用到如图1①、图1②所示的两个基本图形.

（1）如图1②，易知AC + BC = A'C + BC = A'B，要证明AC + BC

（2）如图2，显然最短路径必须经过正方形右下角的顶点D，根据“两点之间，线段最短”，可知B，D间的最短路径是线段BD，而A，D位于直线l的同侧，运用（1）中的方法，作点A关于直线l的对称点[A']，连接A'D交直线l于点C，则A到直线l再到D的最短路径是A—C—D，进而找到了最短路径为A—C—D—B，即在点[C]处建燃气站，铺设管道的最短路线是折线[ACDB]（其中点[D]是正方形的顶点）.

[原题延伸]

变式1 在三角形中研究最短路径.

例2 如图3，等腰三角形ABC底边BC的长为4 cm，面积是12 cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为_____________cm.

解析：如图4，连接AD，∵点D是等腰三角形ABC的边BC的中点，∴AD⊥BC.

由S△ABC = 12 cm2，可得AD = 6 cm.

∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，

∴AD的长为BM + MD的最小值，∴△BDM的最短周长 = （BM + MD） + BD = 8（cm）. 故应填8.

变式2 在正方形中研究最短路径.

例3 如图5，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP + EP最小值的是（ ）.

A. AB B. DE C. BD D. AF

解析：如图6，作E关于BD的对称点E′，连接AE′交BD于点P，

∴AP + EP的最小值为AE′.

∵E为AD的中点，∴E′为CD的中点.

∵四边形ABCD是正方形，∴AB = BC = CD = DA，∠ABF = ∠AD E′ = 90°，

∴DE′ = BF，∴△ABF ≌ △AD E′，∴AE′ = AF，

∴AF等于AP + EP的最小值. 故选D.

变式3 在直角坐标系中研究最短路径.

例4 如图7，点M，N的坐标分别为（1，4）和（3，0），点Q是y轴上的一个动点，且M，N，Q三点不在同一直线上，当△MNQ的周长最小时，求点Q的坐标.

解析：如图8，作点N关于y轴的对称点N′，连接MN′交y 轴于点Q，

则此时△MNQ的周长最小.

∵点N的坐标是（3，0），∴点N′的坐标是（-3，0）.

过点M作MD⊥x轴，垂足为点D. ∵点M的坐标是（1，4），∴N′D = MD = 4，

∴∠MN′D = 45°，∴N′O = OQ = 3，即点Q的坐标是（0，3）.

变式4 在实际问题中研究最短路径.

例5 如图9，草地边缘OM与小河河岸ON在点O处形成30°的夹角，牧马人从A地出发，先让马到草地吃草，然后再去河边饮水，最后回到A地. 已知OA = 2 km，请在图中设计一条路线，使所走的路径最短，并求所行的整个路程.

解析：如图9，分别画出点A关于OM，ON的对称点B，C，

连接BC，分别交OM，ON于点D，E，连接AD，AE，

则线段AD，DE，EA即为所走的最短路径.

由题意得OB = OA = OC = 2，∠BOC = 60°，∴△OBC为等边三角形，∴BC = 2.

故所行的整个路程为2 km.

（作者单位：江苏省兴化市戴泽初级中学）