轴对称典型易错题

王华君

【专 练】

1.“致中和，天地位焉，万物育焉.”对称美是我国古人和谐平衡思想的体现，常被用于建筑、器物、绘画、标志等作品的设计上，使对称之美惊艳千年时光. 在下列与扬州有关的标识或简图中，不是轴对称图形的是（ ）.

2.在平面直角坐标系中，点（3，2）关于x轴对称的点的坐标为（ ）.

A. （-3，2）  B. （-2，3）  C. （2，-3） D. （3，-2）

3. 如图1，在[△ABC]中，按以下步骤作图：①分别以点[B]和[C]为圆心，以大于[12BC]的长为半径作弧，两弧相交于点[M]和[N];②作直线[MN]交[AC]于点[D]，连接[BD]. 若[AC=6]，[AD=2]，则[BD]的长为（ ）.

A. 2 B. 3 C. 4 D. 6

4. 等腰三角形一个内角为70°，则另外两个内角分别是（ ）.

A. 55°，55°    B. 70°，40°或70°，55°

C. 70°，40°    D. 55°，55°或70°，40°

5. 圖2是以正方形的边长为直径，在正方形内画半圆得到的图形，则此图形的对称轴有（ ）.

A. 2条  B. 4条 C. 6条 D. 8条

6. 如图3，在等腰三角形ABC中，BD为∠ABC的平分线，∠A = 36°，AB = AC = a，BC = b，则CD 等于 （ ）.

A. [a+b2] B. [a-b2] C. a - b D. b - a

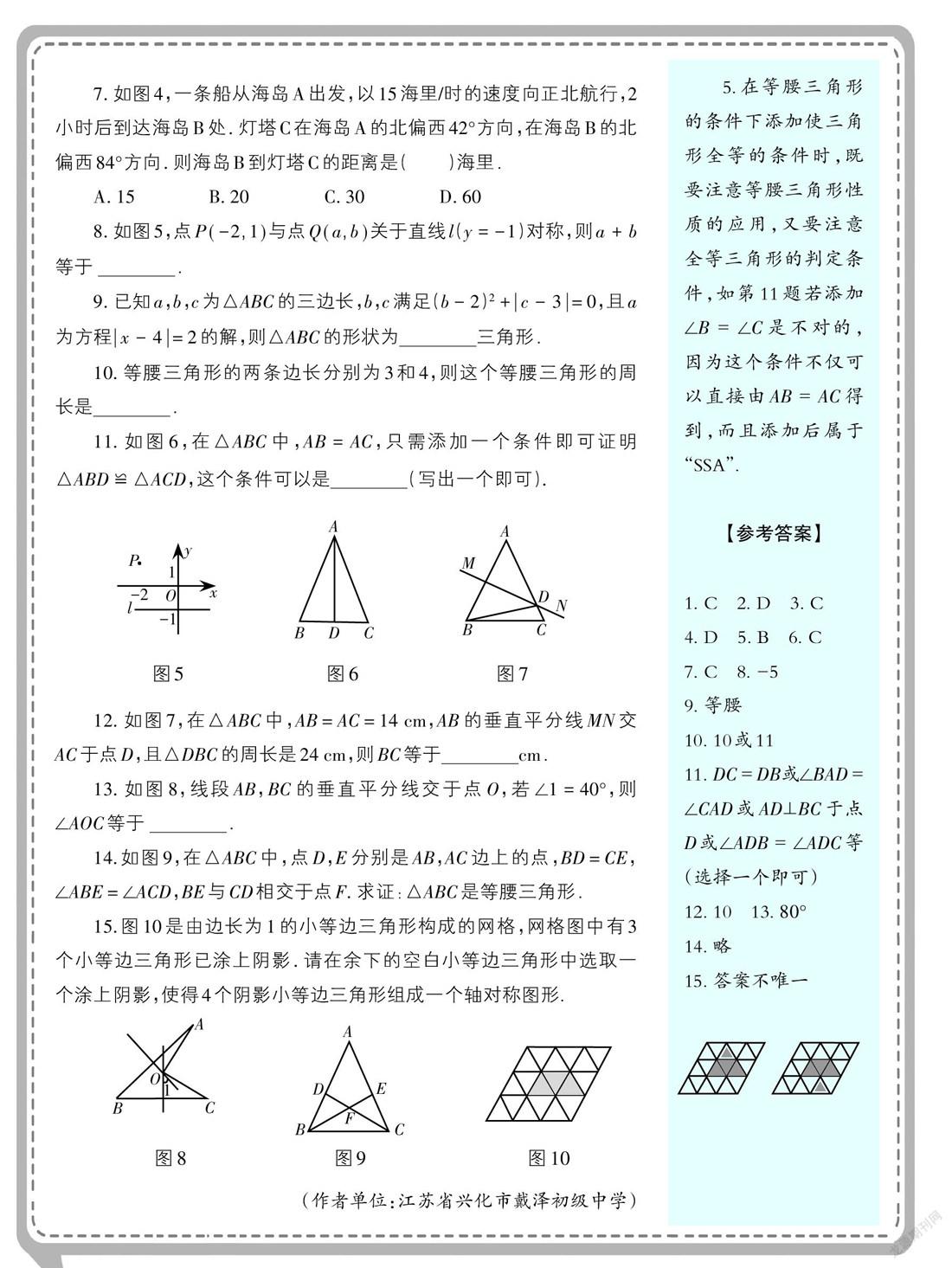
7. 如图4，一条船从海岛A出发，以15海里/时的速度向正北航行，2小时后到达海岛B处. 灯塔C在海岛A的北偏西42°方向，在海岛B的北偏西84°方向. 则海岛B到灯塔C的距离是（ ）海里.

A. 15 B. 20 C. 30 D. 60

8. 如图5，点[P（-2，1）]与点[Q（a，b）]关于直线l（[y=-1]）对称，则[a+b]等于 __________.

9. 已知a，b，c为△ABC的三边长，b，c满足（b - 2）2 + [c-3]=0，且a为方程[x-4]=2的解，则△ABC的形状为__________三角形.

10. 等腰三角形的两条边长分别为3和4，则这个等腰三角形的周长是__________.

11. 如图6，在△ABC中，AB = AC，只需添加一个条件即可证明△ABD ≌ △ACD，这个条件可以是__________（写出一个即可）.

12. 如图7，在△ABC中，AB=AC=14 cm，AB的垂直平分线MN交AC于点D，且△DBC的周长是24 cm，则BC等于__________cm.

13. 如图8，线段[AB]，[BC]的垂直平分线交于点[O]，若[∠1=40°]，则[∠AOC]等于 __________.

14.如图9，在△ABC中，点D，E分别是AB，AC边上的点，BD=CE，∠ABE=∠ACD，BE与CD相交于点F. 求证：△ABC是等腰三角形.

15.图10是由边长为1的小等边三角形构成的网格，网格图中有3个小等边三角形已涂上阴影. 请在余下的空白小等边三角形中选取一个涂上阴影，使得4个阴影小等边三角形组成一个轴对称图形.

（作者单位：江苏省兴化市戴泽初级中学）

【注意事项】

1. 要正确理解轴对称图形的概念，准确判定对称轴的数目，规范构造轴对称图形.如第1题、第5题、第15题，其中第15题答案不唯一.

2. 要注意等腰三角形中边与角问题的分类讨论，谨防漏解与多解，如第4题中70°的角可为底角，也可为顶角;而第9题中2，3，6不能作为三角形的三边.

3. 要灵活运用等腰三角形的性质，特别是“三线合一”，做到知其一可以得其二，进而简捷解决问题，谨防重复推理.如第6题、第11题、第12题等.

4. 注意线段垂直平分线与等腰三角形间的关联，若有前者，则必定有后者.如第3题、第12题、第13题.

5.在等腰三角形的条件下添加使三角形全等的条件时，既要注意等腰三角形性质的应用，又要注意全等三角形的判定条件，如第11题若添加∠B = ∠C是不对的，因为这个条件不仅可以直接由AB = AC得到，而且添加后属于“SSA”.

【参考答案】

1. C 2. D 3. C

4. D 5. B 6. C

7. C 8. -5

9. 等腰

10. 10或11

11. DC = DB或∠BAD =

∠CAD或AD⊥BC于点D或∠ADB = ∠ADC等（选择一个即可）

12. 10 13. [80°]

14. 略

15. 答案不唯一