一种随机布设的声源定位温度补偿算法研究*
崔林林,李 斌,崔卫丽,原 方
(1.中原工学院机电学院,河南 郑州 450007;2.中原工学院计算机学院,河南 郑州 450007)
基于到达时延差(TDOA)的声源定位算法具有运算量小、硬件成本低、算法简单易实现、定位精度较高的特点,使得该算法在工程中的应用非常广泛。基于TDOA的被动声定位技术是通过测得声源到声传感器阵列的时延信息,然后采用特定的定位算法进行解算,进而得到声源在空间中的位置信息[1-2]。在利用TDOA解算声源坐标的过程中,影响最终定位精度的因素有很多,除公式推导过程中的舍入误差、阵元自身的定位误差外,还存在例如声速(温度[3]和风速[4])、计时、声传感器[5]、信号传输等客观因素的影响[6]。在尽可能地确保声学算法本身的定位精度[7]、阵元布设[8]的定位精度以及一些客观影响因素外,影响定位精度的主要因素为声速的获取精度。
而在被动声定位算法[9-10]中,工程上通常采用声速的经验计算公式:c=331.45+0.61T,其中T为温度。由此可见,此时温度成为影响声速[11]的主要因素。实验结果显示测量温度接近常温(25℃左右)时,实验值与理论值基本一致;测量温度与室温相差较大时,实验值与理论值偏差较大[12]。
1 随机布设阵元的声源定位算法
本文的实验对象为一种随机布设阵元的声源定位算法,该算法引用作者之前发表的论文[13]。现做简单介绍如下。
设定声源坐标为(x,y,z),阵元i的坐标为Ni(xi,yi,zi),声程差为Si,Li为阵元i到阵元1的距离,其中i>4,中心阵元坐标为N0(x0,y0,z0),声源到中心阵元的距离为S0。图1为声传感器分布示意图。
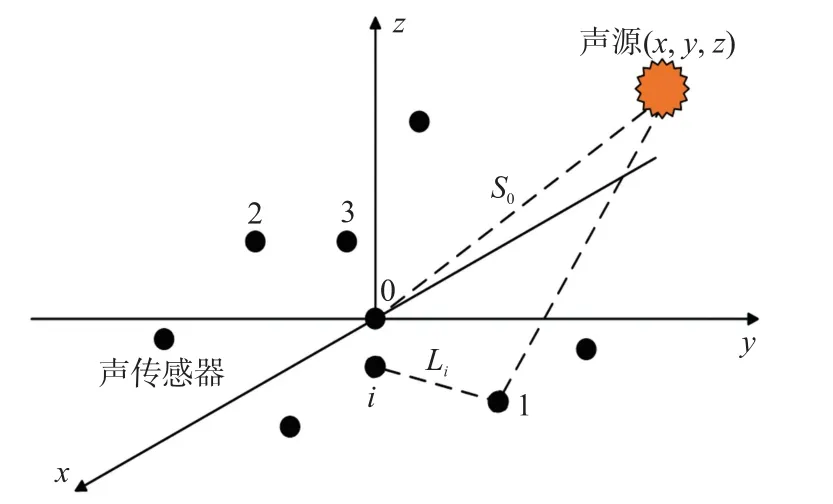
图1 声传感器分布示意图
根据空间几何关系可得:
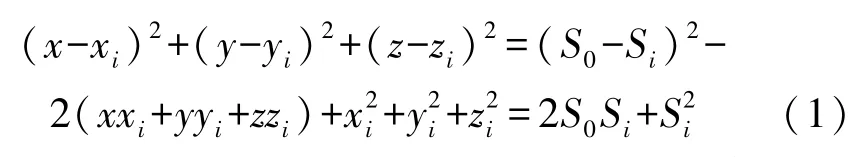
将中心阵元及另外3个阵元的坐标代入式(1),并将其分解合并,可得:
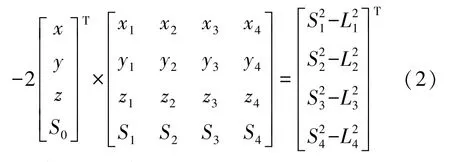
为方便起见,将式(2)写成:

式中:W为声源坐标及声源与中心阵元的距离组成的一维向量;K为4个阵元的坐标及声程差组成的4×4的矩阵;Q为组成的一维向量。
如果矩阵K可逆,在实际的实验过程中,非常容易满足K可逆的条件,于是可得:

2 温度补偿算法
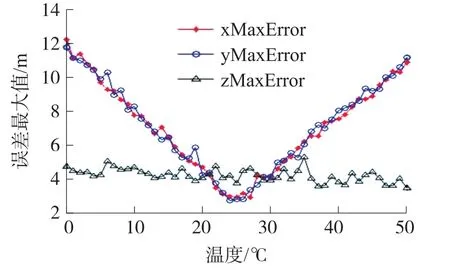
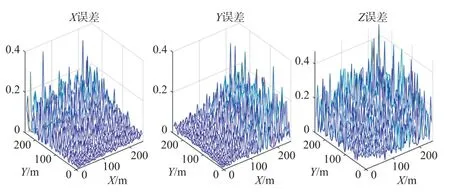
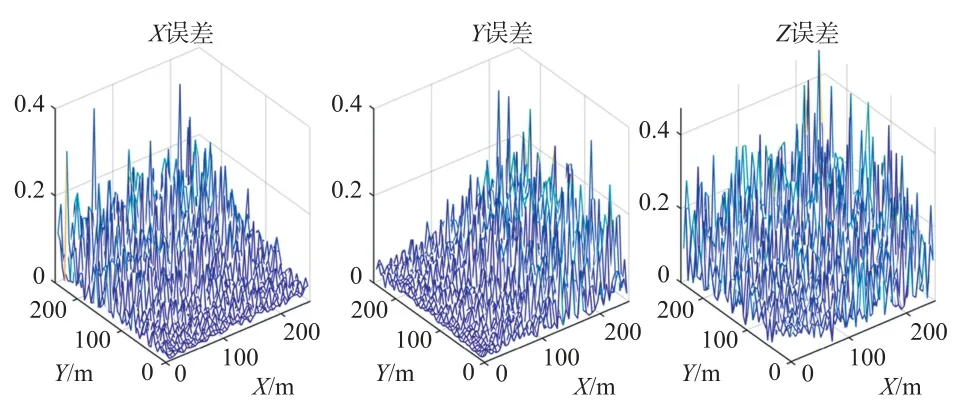
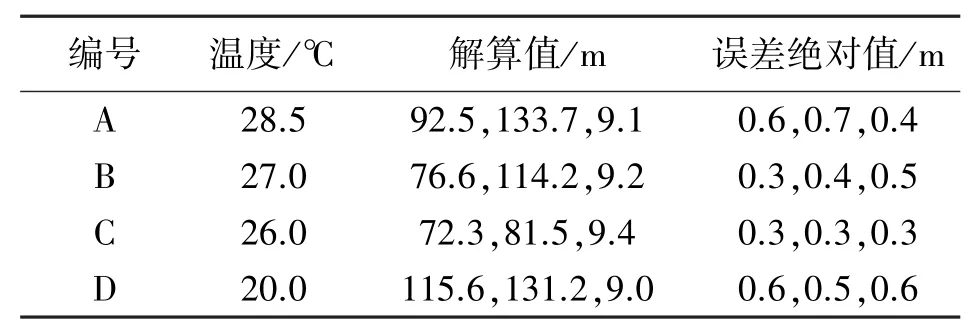
通过对上述随机布设阵元的声源定位算法进行仿真,采用蒙特卡洛仿真方法[14],设定蒙特卡洛次数为2 000次,可得结果如下:在区域{(x,y,z)|-100 设定当前的时延标准差[15]为60μs。温度的变化区间为0到50℃。特卡洛次数为2 000次。这里选取三个点进行分析,这三个点分别位于X轴,Y轴及过零点与X轴夹角45°的线上,坐标分别为A点(80、0、1)、B点(0、80、1)及C点(80、80、1),单位m。之所以选择A点、B点及C点,是因为遍历所有点进行讨论的意义不明显,而这3个点为具有代表性的声源点,是为了描述声源定位算法的误差随温度的变化规律。A点、B点及C点的随温度变化的误差最大值的绝对值曲线如图2~图4所示,其中在x坐标的最大误差值的绝对随温度的变化曲线为星号连线;y坐标的最大误差值的绝对随温度的变化曲线为圆圈连线;z坐标的最大误差值的绝对随温度的变化曲线为三角连线。 图2 A点的温度误差曲线 图3 B点的温度误差曲线 图4 C点的温度误差曲线 由图2~图4可知,A、B、C三个声源点坐标的误差最大值的绝对值关于25℃时对称分布。其中,A点的x坐标误差最大值、B点y坐标误差最大值及C坐标x和y坐标误差最大值随温度的变化呈现先行变化。可利用此情况作为温度补偿算法的判定条件。首先,利用随机布设阵元的声源定位算法解算出声源点的坐标(x1,y1,z1);其次,比较abs(x1)和abs(y1),如果abs(x1)>abs(y1),则以x1的值为判断标准(由于仿真和实验结果均表明x、y坐标的解算误差随远离坐标轴的方向而逐渐增大),此时利用温度补偿程序生成温度补偿算法的三维矩阵[Y;Z;X],由当前解算出来的声源点坐标的x1值确定该三维矩阵的第X页,然后由声源点坐标的y1和z1值确定第X页中Y和Z交互的点,反之亦然;最后,根据三维矩阵[Y;Z;X]中的温度补偿斜率值对声源点坐标(x1,y1,z1)进行补偿。具体补偿过程如下:若声源点坐标值为正,温度小于25℃时,用解算值减去补偿值作为修改值,温度大于25℃时,用解算值加上补偿值作为修改值;反之亦然。此时可得引入温度补偿算法后的修改值(x2,y2,z2)。 仿真采用蒙特卡洛方法,次数为1 000次。当温度为25℃时,坐标误差如图5所示,坐标x和坐标y的最大误差小于0.4 m,坐标z的最大误差小于0.8 m;当温度为34℃时,坐标误差如图6所示,坐标x和坐标y的最大误差小于12.7 m,坐标z的最大误差小于0.5 m。 图5 未引入温补时,温度为25℃时的误差 图6 未引入温补时,温度为34℃时的误差 同样的情况下,温度为25℃时,坐标误差如图7所示,坐标x和坐标y的最大误差小于0.4 m,坐标z的最大误差小于0.8 m;温度为34℃时,坐标误差如图8所示,坐标x的最大误差小于7.1 m,坐标y的最大误差小于7.1 m,坐标z的最大误差小于0.17 m。 图7 引入温补时,温度为25℃时的误差 图8 引入温补时,温度为34℃时的误差 针对2.1和2.2的结果进行分析:比较图5和图7的结果,当测试环境的温度在25℃时,是否引入温度补偿算法对声源点的定位精度几乎没有影响;比较图6和图8的结果,是否引入温补算法对声源点的定位精度有着较大的影响。当设定温度为34℃的时候,比较结果可以可知加入温度补偿算法后,坐标x和坐标y的最大误差由12.7 m下降至7.1 m,且除局部存在峰值误差外,整体误差变化较为平坦;坐标z的最大误差由0.5 m下降至0.2 m。 以炮仗作为实验的声源,在郑州的郊区进行声定位实验。具体实验步骤如下:第一步,通过全站仪及GPS设备(简称“打点设备”)在实验区域内随机且分散地打4个点,这4个作为阵元点。第二步,在通过打点设备随机选取声源点,选好后通过三脚架防止炮仗。第三步,点燃炮仗,代入定位系统和补偿系统进行声源坐标的解算。其中第二步和第三步总计做了4组实验。这4个声源点的坐标分别是 A(93.1,133.0,9.5),B(76.9,114.6,9.7),C(72.0,81.2,9.7),D(115.0,130.7,9.6),单位m。 实验中采用基于ZigBee技术的CC2530模块进行声信号的数据采集及信号传输工作。声传感器接入CC2530模块。实验中的温度为每次实验中现场采集的温度。未引入温补算法的解算结果如表1所示,引入温补算法的解算结果如表2所示。所用的声传感器为普通的咪头麦克风,如图9所示。该咪头麦克风的重要参数为:频率响应为50 kHz~20 kHz,灵敏度为:-38 dB~-50 dB,方向特征为全指向。 表1 未引入温补算法的解算结果 表2 引入温补算法的解算结果 图9 声传感器 由表1的4组解算结果可知,温度远离25℃的定位结果误差越大,也符合仿真结果。通过比较表1和表2可知,引入温补算法的解算结果相较于未引入温补算法的解算结果而言,x坐标的误差均值小了0.23 m,y坐标的误差均值小了0.25 m,z坐标的误差小了0.18 m。由此可知,引入温度算法后的声定位算法较好地解决了因温度变化引起的误差。 在进行声学定位试验或某些民用及军用产品试验的时候,由于现场的测试环境中不可能一直保持类似室温环境(25℃左右),如果当前所使用的声源定位算法受声速影响,此时便不能忽略温度对定位结果的影响。针对当前提出的问题,以作者之前提出的一种随机布设阵元的声源定位算法为基础,进行了不同温度区间的温度补偿算法的仿真解算。结果证明,引入该温度补偿算法可有效地改善温度对声源点定位结果的影响。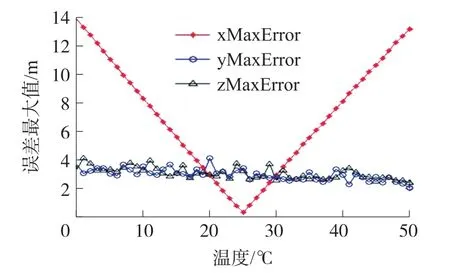

2.1 未引入温补算法

2.2 引入温补算法
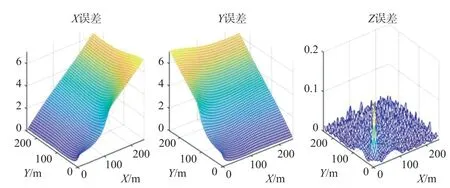
3 实验


4 结论

