地铁车辆轮对外形尺寸在线检测系统

程中国

(青岛地铁集团有限公司，266045，青岛//高级工程师)

地铁车辆运行中轮对承受着车辆自重及载重，同时还要传递车辆与钢轨间的驱动力和制动力，致使车轮踏面及轮缘会出现磨损，易导致外形尺寸超限，影响行车安全[1-2]。

目前车辆轮对尺寸检测主要分为静态检测和动态检测[3]。静态检测工具主要是第四种检查器和轮径尺。动态检测分为两类：一类是通过镟轮设备在镟轮过程中兼顾的轮对尺寸测量功能进行检测；另一类是通过轮对外形尺寸在线检测系统[4-5]进行检测。本文介绍“轮对外形尺寸在线检测系统”。该系统采用光截图像法对运行车辆轮对尺寸进行在线检测，实现轮缘高度、厚度、轮对内侧距、车轮直径的自动测量。基于LS-SVM预测模型实现对车轮磨耗趋势的预测分析，并与BP神经网络算法预测模型进行对比分析。基于尺寸检测系统的数据与LS-SVM预测模型的研究成果，将其运用到车轮经济镟修中，产生了较好的社会经济效益。

1 轮对外形尺寸在线检测系统

1.1 系统组成

轮对外形尺寸在线检测系统主要由现场基本检测单元、车辆信息检测单元、轨旁综合数据处理单元及远程数据分析单元组成，如图1所示。

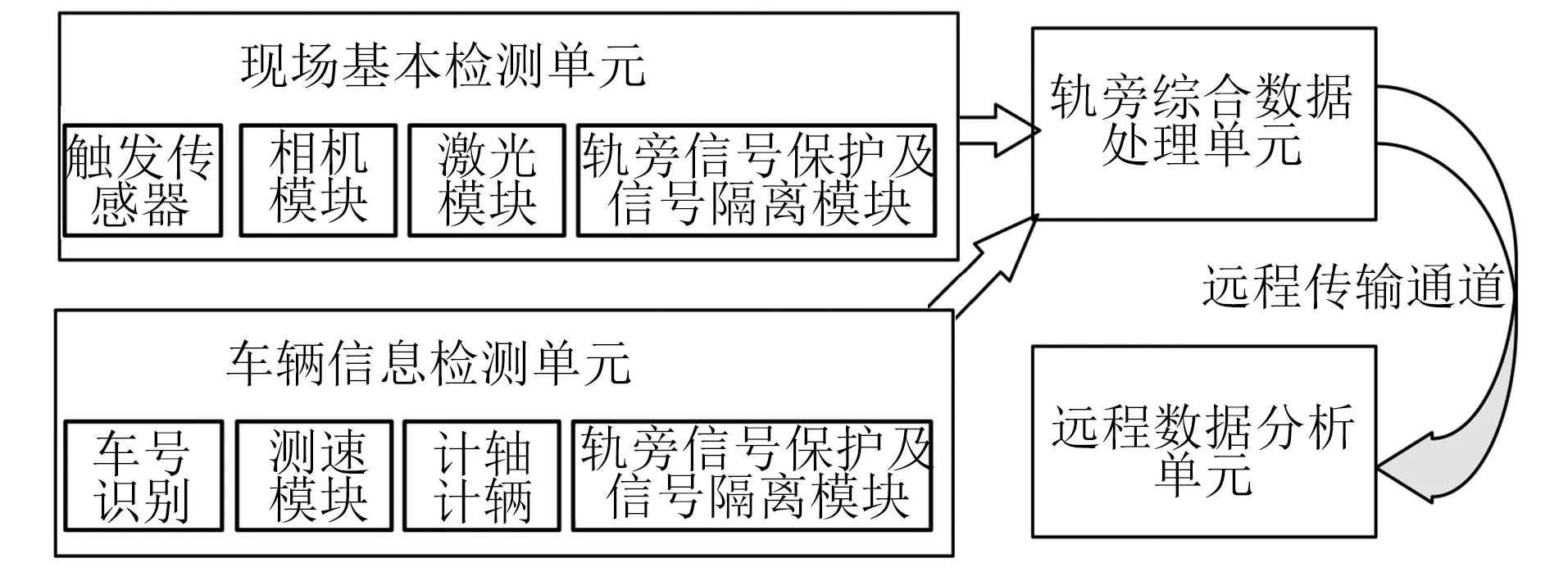
图1 轮对外形尺寸在线检测系统组成结构

1.2 轮对外形尺寸在线检测原理

轮对外形尺寸在线检测系统的数据采集主要由分布在轨道两侧的8个线光源和相机实现，检测系统传感器现场布置方式如图2所示。车辆经过时，激光线投射到车轮踏面上，轨道外侧LD投射在车轮的上方，内侧LD投射在车轮的下方，如图3所示。CCD相机获取上述光截线图像，并使获取的图像凸显出踏面轮廓线，如图4所示。相机获取到踏面轮廓曲线后，通过拟合算法，实现内外侧曲线自动拼接合成一条完整的踏面轮廓曲线，系统再将实际完整的踏面轮廓曲线与标准的轮廓曲线进行对比分析，最终计算得出车轮的轮缘高度、厚度、轮对内侧距、车轮直径等参数。车轮外形关键参数如图5所示。

图2 轮对外形尺寸在线检测系统现场布置方式

图3 轮对外形尺寸在线检测系统激光线位置

图4 实际踏面轮廓曲线

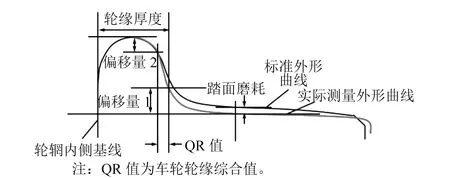
图5 车轮外形关键尺寸

1.3 数据展示平台

轨旁综合数据处理单元完成轮对尺寸数据处理后，通过局域网传输至DCC(车辆段控制中心)，传输的信息包含车辆信息及对应车轮的轮对尺寸检测数据。

2 数据预测模型及趋势分析研究

2.1 LS-SVM预测模型

最小二乘支持向量机(Least-Squares SVM，LS-SVM)是在SVM(支持向量机)基础上，通过将限制条件中的不等式约束转变为等式约束，将经验风险值变为偏差的二次方，将复杂的二次规划问题求解转变为常见的线性规划问题求解[8]。LS-SVM改进后的模型计算效率更高，更加适合求解大规模问题，同时得到的训练模型精度也更高。

1) 最小二乘原理：设存在一组实测数据(x,y)，且x=(x1,x2,…，xm)T∈Rn,y∈R，满足如下一种理论函数：

y=f(x1;w1,…，wm)

(1)

其中wi(i=1,…,m)是未知待求参数。

为了获取函数y=f(x1;w1,…，wm)待定参数的最佳取值，根据实际问题，给出另外n对实测数据(xi,yi)(i=1,…，n,n≫m)。使得线性方程组的目标函数：

(2)

取最小值时的参数wi(i=1,…,m)，这类称为最小二乘法问题。用几何语言也可称作最小二乘拟合[9]。

公式(2)中，实测数据对中的函数值与公式(1)中的理论函数差值称为残差。即：

ri(w)=yi-f(xi;w1,…，wm)(i=1,…,n)

(3)

其中，w=(w1,w2,…,wm)T∈Rm。为了提高拟合的准确率，一般采用各个实测数据求残差，计算他们的加权平方和作为最终的函数，即求参数wi使公式(4)取得最小值。

(4)

其中，γi>0为在点(xi,yi)处的权因子。该权值γi一般解释为该测量点在实际中出现的频次。

2) 最小二乘支持向量机：用最小二乘法建立最优化模型，没有不敏感损失函数，计算难度降低。其优化模型如下：

(5)

其中：C为正则化参数(惩罚因子)，e为实际值与回归函数间的误差；w为权值向量，b为偏置向量。为求最优化问题的解，构造一个拉格朗日函数，其中ak为拉格朗日乘子：

L(w,b,e,a)=J(w,e)-

(6)

根据最优化问题的KKT(Karush-Kuhn-Tucker)条件，将式(6)对w，b，e，ak求偏导得：

(7)

消除变量w，e，即可得到式(8):

(8)

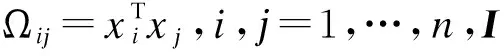
a=(a1,…,an)T,y=(y1,…,yn)T。

因为方程组(8)是非奇异矩阵，可以求出a,b的解。因此，得到最小二乘支持向量机的回归估计函数：

(9)

其中，K(xk,xl)为满足Mercer条件的核函数，作用是从原始空间中抽取特征，映射到高维特征空间，解决原始空间线性不可分的问题。综合上述公式推导分析，公式(9)即为本文预测轮对磨耗趋势需要用到的函数模型。

2.2 车轮磨耗趋势分析

利用青岛地铁2号线1年内的轮对历史检测数据作为训练样本进行LS-SVM模型训练，对最近一次检测数据进行预测。为了验证LS-SVM模型的精度，选取了BP神经网络预测模型进行对比，两种预测模型预测结果如图6～7所示。

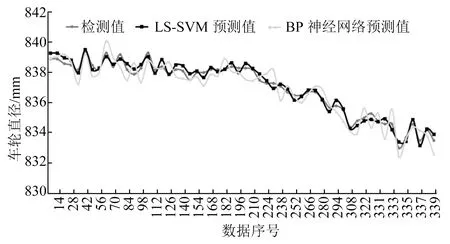
图6 利用LS-SVM和BP神经网络预测车轮直径

选取前300个样本为模型训练样本数据，最后8次数据为预测值。车轮直径LS-SVM的预测值平均误差为0.3 mm，BP神经网络的预测值平均误差为0.5 mm。轮缘高度LS-SVM的预测值平均误差为0.1 mm，BP神经网络的预测值平均误差为0.2 mm。因车轮磨耗存在一定的周期重复性。本文目前预测基于1年周期内的时间预测，该周期内车轮直径从839.4 mm磨损到833.0 mm，轮缘高度从28.7 mm增长到31.9 mm，车轮磨耗特征均体现明显。基于1年周期的特征可扩展至更长周期的车轮尺寸参数预测。因此，本文研究的LS-SVM预测模型对于车辆轮对外形尺寸预测具有较好的长周期适应性和较高的精度。

图7 利用LS-SVM和BP神经网络预测轮缘高度

3 轮对外形尺寸在线检测系统实际运用

青岛地铁2号线已将上述预测结果用来指导车辆轮对检修。在轮对外形尺寸在线检测系统运用之前，传统车轮检修需要人工使用第四种检查器进行测量，完成1列列车测量需要2人工作4 h,平均误差约0.5 mm。采用轮对尺寸在线检测系统后，轮缘高度、厚度测量精度约0.2 mm,轮对内侧距、车轮直径测量精度约0.5 mm,完成1列列车所有车轮的测量仅需3 min，测量效率和质量得到明显提高。

在轮对尺寸在线检测系统基础上，增加磨耗趋势预测模型，可有效规划轮对总体的使用寿命，提前预测和规划轮对镟修周期。例如：在正常情况下，列车车头和车尾的轮对磨损较为严重，在镟修过程中因考虑到镟修模型，须对整列车进行统一规格的镟修，这导致列车中间部分的车轮浪费严重。借助于预测模型后，可实现列车两端车厢轮对与中间车厢轮对不同的寿命周期预测，从而采用两种镟修模型，避免列车中间车厢的轮对重度镟修，可延长中间车厢轮对的使用周期。

4 结语

本文介绍了车辆轮对外形尺寸在线检测系统的组成、尺寸检测原理和数据展示平台。同时采用LS-SVM算法对车轮直径、轮缘高度值的变化趋势进行了预测分析，用来指导轮对检修，在实际生产中发挥了较大的作用。因现场的数据训练样本仍然较少，该系统的预测精度还有进步的空间，后续还需加强对现场实际运用数据的搜集以及训练模型的完善。