粉质黏土地层盾构施工地表沉降关键参数分析与预测*

杨 益 李兴高 蒋兴起 金大龙

(1.北京交通大学土木建筑工程学院，100044，北京；2.北京交通大学城市地下工程教育部重点实验室，100044，北京；3.常州市轨道交通发展有限公司，213022，常州∥第一作者，博士研究生)

盾构法施工由于其技术和经济的优越性，且能够在不影响城市正常功能的情况下快速完成隧道建设，已成为地铁区间隧道建设的主流施工方法。在建构筑物密集的城市区域，盾构掘进时不可避免地会对土体产生扰动从而造成土体位移场发生变化，位移过大则会对邻近建构筑物安全性造成威胁[1]。长久以来，大量学者致力于隧道施工引起的地表沉降和变形预测研究。但对于一个特定地区来说，由于地层环境及施工水平的差异，隧道施工引起的地层沉降有其自身的特点，准确预估地层沉降对指导施工有重要意义。

目前，预测隧道引起地层变形的主要方法有经验法、解析法、数值模拟法。早在1969年，Peck建立了隧道开挖引起地表沉降的经验公式[2]，是经验法的代表，因其具有简单、适用等特点，成为应用最广泛的分析方法。随着对盾构施工引起地层沉降的深入研究，解析方法逐渐发展，目前主要的解析方法包括应力函数法[3]、复变函数解[4]和虚像法[5]等，可以求解不同边界条件下地层变形情况。此外，随着计算机技术的发展，数值模拟方法越来越多地应用于预测地层变形。有限元[6]、有限差分[7]等方法能考虑到复杂的施工工艺、地质条件等影响因素，具有其独特的优势；但这些方法的建模过程较复杂，参数较多、较难确定。

本文基于常州地铁1号线、2号线大量的地表沉降监测数据，对Peck公式在常州地区的适应性进行了分析，并给出了预测盾构开挖引起的横向地表沉降相关计算参数的取值范围。基于隧道结构-土体相互作用理论，并考虑地层损失和盾构施工荷载，建立了适用于常州地铁当前施工水平的预测盾构掘进时地表隆沉的计算方法，并与实测数据进行了对比。可为后续类似地层中地铁施工地表隆沉预测提供参考。

1 常州地铁工程概况

常州地铁1号线一期工程线路全长约 34.076 km，其中，地下线长31.474 km，高架线长2.189 km，敞开段长0.413 km，目前已全线贯通并通车；2号线一期工程线路起于西部青枫公园站，终于东部颜家站，工程线路全长19.8 km，其中地下线长约18.23 km，目前仍在建设中。常州地铁工程主要采用土压平衡式盾构掘进，盾构机直径6.34 m，管片外径6.2 m。

常州市地处长江下游三角洲苏南平原，地形较为平坦，区域地质构造较稳定。地质勘察资料显示，地下区间盾构隧道主要穿越粉质黏土层，土体多呈软塑～流塑状，具有含水量较高、孔隙比大、强度低、压缩性较高等不良工程特性，同时还具有低渗透性、触变性和流变性等软土特点。

2 横向地表沉降分析

2.1 地表沉降预测的Peck方法

Peck提出了地层损失的概念，且假定实际土体损失体积等于沉降槽的体积。同时，基于对大量隧道开挖引发的地表沉降测试数据的分析结果，Peck提出了估算隧道开挖地表下沉的实用方法，即距隧道中线x处的地表沉降值S(x)可按式(1)计算[2]：

(1)

式中：

Smax——地表最大沉降量，被认为位于隧洞轴线位置；

x——从隧道轴线到计算点的距离；

i——沉降槽宽度系数，代表从沉降曲线中心点到拐点的距离。

对于盾构施工的不排水条件，最大沉降值Smax可按式(2)计算[3]：

Smax=0.313VLD2/i

(2)

式中：

VL——单位长度地表沉降槽的体积占隧道开挖名义体积的百分比，称为地层损失率；

D——盾构开挖直径。

虽然Peck公式因其简便性、合理性被国内外广泛应用于预测盾构隧道开挖引起的地表沉降[8]，但对于具体工程而言，应用Peck公式对地表沉降进行估算需要确定两个参数：沉降槽宽度系数i和地层损失率VL。其中，VL与施工工艺、施工管理水平及土层性质等因素相关，一般可依据经验取值或预先在试验段确定。当VL一定的情况下，i值决定了地表沉降的影响范围。长期以来国内外对i的取值问题，仍未形成统一的理论。i的取值与土层的性质、隧道埋深和洞径等均有关系，目前的研究均认为i值与隧道埋深Z呈正相关规律。即在相同VL的条件下，隧道埋深越大，沉降槽越宽，Smax越小，沉降曲线宽而浅。

2.2 常州地铁地表横向沉降的统计参数

对于一个确定的工程而言，盾构施工引起的地表位移取决于沉降槽宽度系数i和地层损失率VL。VL决定了沉降的大小，i决定了沉降槽的形状。文献[9]根据在伦敦地区的经验，认为i与隧道埋深Z之间可以建立简单的线性关系：

i=KZ

(3)

式中：

K——沉降槽宽度参数。

当隧道的直径D和埋深Z已知时，准确估计VL与K值成为预测地表横向沉降的关键。在一个地区特定的地质条件下，VL与K值具有一定的普遍规律。选取常州地铁1号线4个区间共59个横断面的监测数据进行分析，隧道埋深Z在9.4～26.7 m之间，涵盖了目前常州市地铁穿越的各类典型粉质黏土地层。对选取的断面进行Peck曲线拟合而得到Smax和i，通过换算得到VL以及K值。

图1 a)为VL与深跨比Z/D的关系图。由图1 a)可知，在当前施工水平条件下，常州地铁采用土压盾构施工的VL控制值在1.5%以下。当Z/D小于3时，VL值普遍为1%以下；当Z/D大于3时，其中一些断面的VL值超过1%，以隧道上覆地层为粉砂层居多。

图1 b)为地层损失率VL的分布范围统计结果。由图1 b)可知，粉砂夹粉土层与粉砂夹粉质黏土层的分布相似，VL值在0～0.25%范围内的占50%以上，控制地层损失的难度较小。上覆地层为粉砂层时，VL值在0.25%～0.5%范围内得占70%左右，控制地层损失的难度较前者更大。整体来看，VL值在0.75%以下的比例在90%以上，可在该范围内取值对地表沉降进行估计。

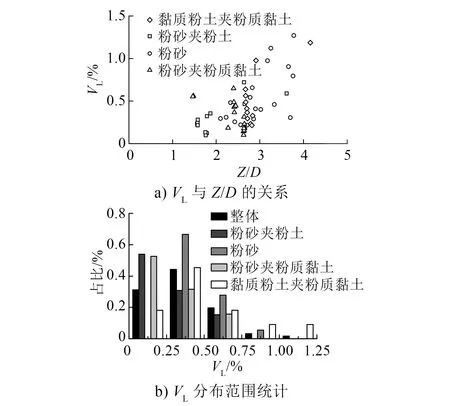
图1 地层损失率VL统计分析结果

图2 a)为i/D与Z/D的关系。尽管不同上覆地层的数据分布较离散，但整体而言，数据点符合公式(3)呈现的线性关系，且绝大部分断面的K值在0.3～0.7范围内。

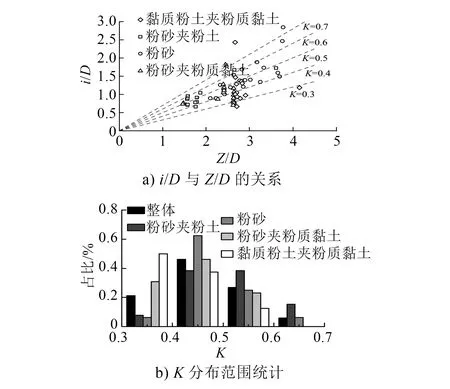
图2 沉降槽宽度参数K统计分析结果

图2 b)为隧道在不同上覆地层中的K值分布统计结果。整体而言，K值在0.3～0.4区间内的约占20%，在0.4～0.5区间内的约占50%，在0.5～0.6区间内的约占30%。粉砂层及粉砂夹粉土层中K值分布在0.4～0.6范围内的断面占80%以上，K值可按此范围进行估计。黏质粉土夹粉质黏土层中K值在0.3～0.5范围内的约占90%，对该地层内的断面，K值可按此范围进行估计。

3 施工过程中的地表位移分析

利用Peck公式并选用合理的预测参数i和VL可以有效预测盾构施工后的横向地表沉降。但在盾构机掘进过程中，由于施工荷载引起的地层变形同样不容忽视。

3.1 盾构机对土体的作用力学模型

文献[10]提出了综合考虑地层损失、盾壳摩擦、附加支护压力、刀盘扭转切削4个方面影响的盾构机对土体的作用力学模型，如图3所示。通过将4个方面各自引起的位移场叠加可以得到盾构掘进引起天然地层位移场。

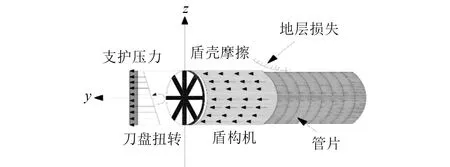
图3 盾构机对土体作用力学模型

3.2 地层损失引起的地表位移

在文献[10]提出的模型中，因地层损失产生的任意一点的竖向位移uzV为：

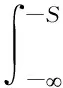
(4)

(5)

(6)

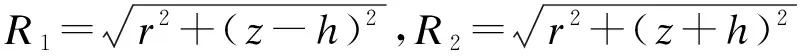
式中：

h——球形空腔中心的覆土深度；

V0——球形空腔引起的体积损失；

H——隧道中心轴线的埋深；

R——隧道断面的半径；

V(x,z)——隧道边界沿环向的收敛位移分布函数；

x,y,z——x,y,z轴的位置坐标；

ξ——隧道开挖长度；

g——用于定义盾尾空隙大小的间隙参数。

根据文献[11]对g的定义，g可以表达为：

g=Gp+u3D+ω

(7)

式中：

Gp——盾构机外缘与衬砌外缘在几何上所形成的空隙；

u3D——因土体挤入隧道工作面产生的三维弹塑性变形等效的径向位移量；

ω——考虑施工精度产生的额外地层损失量。

随着土压盾构技术的发展，在土仓压力设定良好的条件下，开挖面前方土体可基本保持稳定，u3D可以被忽略。同时，由于同步注浆技术的发展，Gp可通过壁后注浆被有效填充。文献[12]基于同步注浆浆体变形试验结果，考虑了壁后注浆体的体积收缩损失，将g修正为：

g=G′p+ω=Gpε+min(G′p,ui/3)

(8)

式中：

ε——壁后注浆体随时间的体积收缩率；

G′p——壁后注浆收缩后的盾构机外缘与衬砌外缘剩余的空隙；

ui——平面应变顶拱的弹塑性位移量。

根据文献[13]的研究成果，ui可定义为：

(9)

式中：

Eu,ν,cu——分别是土体不排水弹性模量、泊松比和抗剪强度；

σv——隧道拱顶的垂直土压力；

Pi——隧道掌子面支护压力。

根据式(8)和式(9)可计算得到当前施工水平及地质条件下的g。

3.3 临时施工荷载引起的地表位移

文献[14]推导出水平和竖向点荷载作用于弹性半无限空间内部某位置时土体中任意一点的位移。对于盾构施工荷载(如盾壳摩擦力、附加支护力、刀盘扭转力)对地层影响的研究，采用Mindlin公式能够得到较为理想的结果[10]。

基于Mindlin公式，可得到附加支护力Δp引起的任一点的竖向位移uzp为：

(10)

式中：

ζ——由Mindlin理论的水平力解确定的格林函数；

ρ——开挖面径向坐标；

θ——开挖面角度坐标。

同理可得盾壳摩擦力f、刀盘扭矩T引起的任一点的竖向位移uzf、uzT。通过叠加上述各分量，可得到盾构隧道施工引起的空间变形uz如下：

uz=uzV+uzp+uzf+uzT

(11)

3.4 常州地区三维沉降预测实例分析

选取常州地铁2号线某位置处监测数据进行实例对比分析。首先估算地层损失引起的地表位移。盾构机参数如下：D=2R=6.34 m；管片外径6.2 m；盾构机长8.68 m。土体泊松比v=0.28，H=17 m。为计算g，根据地勘资料及掘进数据，相关参数取值如下：Eu=11 MPa，cu=10 kPa，σv=0.28 MPa，Pi=0.21 MPa。根据文献[12]中试验结果表明，壁后注浆体在注浆压力192.6 kPa和240.7 kPa作用下的体积收缩率εc均为9.8%，利用式(8)，采用ε=εc=10%可得：

G′p=Gpε=(6.34 m-6.2 m)×0.1=0.014 m

(12)

利用式(9)计算可得，ω=0.014 m，则g取值为0.028 m。则由地层损失引起的地表位移如图4所示。由图4可知，地表位移关于隧道轴线呈对称分布，在隧道横断面上呈现Peck曲线型分布。总体而言，地层损失对地表位移的影响范围大致为隧道轴线两侧各20 m范围内。

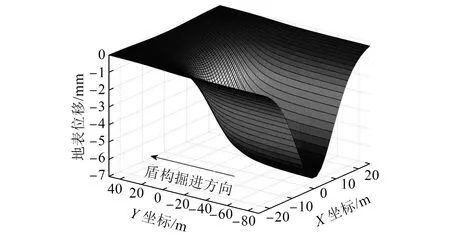
图4 地层损失引起地表竖向位移场

其次，对施工荷载引起的地表位移进行估算。根据盾构机行进参数确定施工荷载计算参数如下：f=40 kPa，Δp=40 kPa，T=2570 kN·m。图5为各施工荷载引起的地表位移场分布。f和Δp引起的地表竖向位移呈现前隆后沉规律。f引起的地表最大隆起值2.7 mm，Δp引起的地表最大隆起值仅为0.06 mm，相较于f而言，Δp对地表隆沉的影响较小。f和Δp对地表位移的影响范围约为刀盘位置前后各40 m、隧道轴线左右各 25 m的范围。T对地层位移场的贡献极小，最大位移量仅0.002 mm，完全可被忽略。

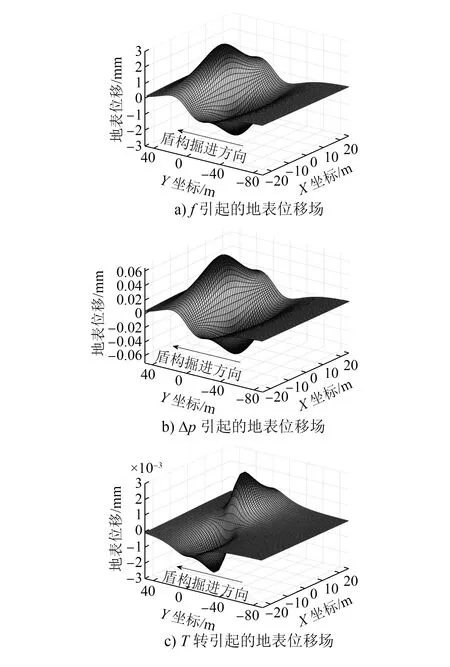
图5 施工荷载引起地表竖向位移场

将图4、图5的位移场叠加，得到图6 a)的预测地表位移场。图6 b)为实测地表位移场。二者对比可知，整体而言，预测值与实测值呈现的位移场规律基本吻合，以隧道轴线为中心线，宽度为50 m的区域内的地表位移场均受到盾构掘进的影响。以刀盘所在位置为分界线，刀盘前方地表产生隆起，刀盘后方地表呈现沉降。从盾构后方横向沉降来看，由于实测时在X方向测点布置存在限制，致使图6中预测位移场的沉降槽宽度较实测值稍宽。从纵向沉降来看，预测位移场中，最大沉降值产生于盾尾后方约5 m的隧道轴线处，最大隆起值产生于刀盘前方约10 m的隧道轴线处。

选取图6 b)中SD3、SD4、SD5等3列测点进行纵向沉降对比分析，结果如图7所示。刀盘位于Y坐标轴零点位置，SD3列测点位于隧道轴线正上方。由图7可知，在Y坐标轴-20～40 m的范围内，预测曲线能较好地反映地表位移的纵向演变规律。但在Y坐标轴-100～-20 m范围内，预测沉降值较实测值更小，原因有以下2个方面：

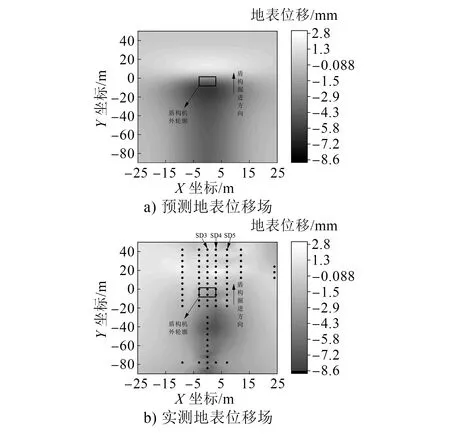
图6 预测与实测地表竖向位移场对比

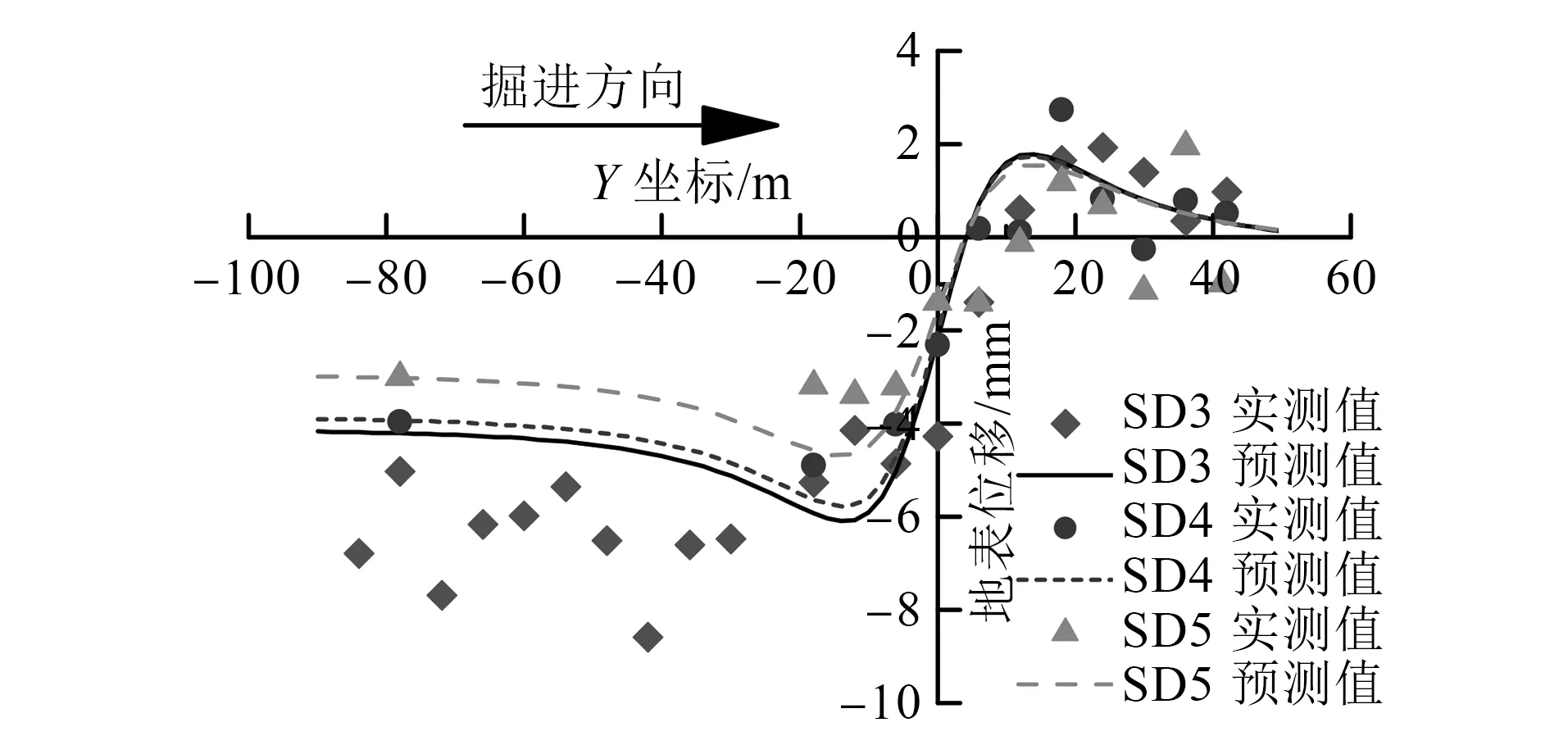
图7 盾构施工引起的预测与实测地表纵向位移对比

1) 预测值关于地层损失对沉降的贡献是基于同步注浆体的体积收缩进行估算的，对注浆体体积收缩的估算可能存在误差；

2) 由于常州地区属于深厚富含承压水地层，土层被盾构掘进扰动之后，超孔隙水压力逐渐消散引起地层产生长期固结沉降，该部分沉降不在预测模型考虑范围内。

4 结论

1) 从常州地区盾构施工的统计数据来看，地层损失率VL在0.1%～0.75%范围内，沉降槽宽度参数K取值在0.3～0.7之间。

2) 考虑地层损失、盾壳摩擦力、附加支护力、刀盘扭转的盾构机对土体的作用力学模型，可以有效预测盾构掘进时刀盘切口后方20 m至前方40 m的地表隆沉。

3) 基于Mindlin解求得的施工荷载对地表位移场的各种作用中，盾壳摩擦力f对地表位移起主要作用，附加支护力Δp的作用较小，刀盘扭矩T的作用可被忽略。