基于创新性思维的《最优化理论与方法》课程教学研究与实践
徐恭贤
(渤海大学 数学科学学院,辽宁 锦州121013)
0 引言
最优化是一门应用相当广泛的学科[1],它研究在一定限制条件下,选取某种方案,以达到最优目标.最优化理论与方法广泛应用于经济计划、国防、工程设计、自动控制、交通运输、通讯、生产管理等重要领域[1-4].为了培养出能适应时代发展需要的应用型数学人才,目前各高校运筹学与控制论、应用数学、计算数学等研究生专业基本都开设了与最优化理论、方法、计算和应用相关的数学课程,并且相关授课教师通过多种改革方法提高了最优化研究生课程的教学效果[5].
目前最优化研究生课程教学中存在的主要问题是教学模式陈旧单一,多数教师采用的教学方式依旧是注重理论讲解和算法实现的讲授式教学.这种教学形式很难调动学生的学习热情和兴趣,多数学生只能课上被动接受知识,参与课堂教学的积极性不高,最终导致教学效果不是很理想.从学生自身来看,多数研究生之所以不能积极、主动地学习最优化课程,主要原因有两个,一个是他们没有将提高科研创新能力作为课程学习的最终目标;另一个是他们没有将课程学习与专业背景和研究方向相融合.因此,我们有必要对最优化课程的传统教学方法进行改革,构建以研究生群体为主体、以研究生创新思维发展为导向的教学新模式.这种教学模式主要采取参与式和研讨式的教学方式,通过理论方法启发引导、实际应用问题的启发式介绍、最优化方法的编程实践与应用、科研项目的参与等有力措施,切实调动学生的学习热情和兴趣,有利于学生自主学习、主动探索、发现问题、解决问题、科学研究、科技创新等能力的提高,从而提升研究生人才培养效果.
鉴于此,结合《最优化理论与方法》课程的特点,以及笔者多年来的研究生教学研究与实践,本文就《最优化理论与方法》课程的教学方法进行了深入分析与研究,提出了针对渤海大学数学科学学院运筹学与控制论、应用数学等专业研究生的教学改革方案,并给出了基于创新性思维的教学方法在本门课程中的教学与实践模式.
1 《最优化理论与方法》课程的教学改革思路和措施
本文将从以下几个方面具体阐述《最优化理论与方法》课程的教学改革思路和措施.
1.1 从单纯讲授式教学转变到讨论、启发式教学
在《最优化理论与方法》课程的教学中,教师应该改变过去陈旧单一的传统讲授式教学形式,在教学实践中始终坚持以学生为主体的教学模式,并设计难易适当的讨论和启发式问题,供学生思考和讨论.通过讨论和启发式教学,可以激发学生学习《最优化理论与方法》课程的主动性,从而有益于学生独立思考能力的锻炼和创新思维的激发.比如在学习如何将不等式约束优化问题转化为与其等价的等式约束优化问题时,教师可以让学生分组讨论如下问题:

例1:将不等式约束优化问题转化为与其等价的等式约束优化问题.其中,x∈Rn,f,gi:Rn→R1为连续可微函数.
考虑到不等式约束gi(x)≤0(i=1,2,…,m)的左边小于等于右边,A组同学认为可以在不等式gi(x)≤0的左边加上非负变量yi∈R1,使其变为等式约束gi(x)+yi=0,从而得到如下等式约束优化问题:

B组同学对A组同学的上述解答提出了质疑.B组同学认为问题(2)与原问题不等价,因为问题(2)漏掉了非负约束yi≥0.B组同学将问题(2)重新表示为:
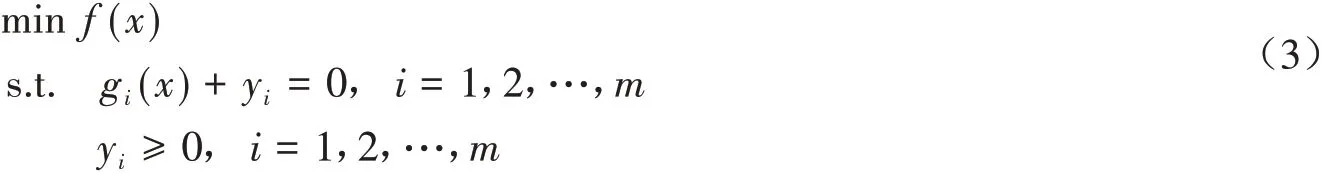
C组同学认为问题(3)不是等式约束优化问题,因为新引入的下界约束yi≥0(i=1,2,…,m)仍然是不等式约束.C组同学认为A组同学在不等式gi(x)≤0的左边加上非负项的想法是正确的,但要保证加上非负项后不能再引入额外的不等式约束.事实上,这种非负项并不唯一,比如y2i,y4i和y6i等.考虑到问题表示形式应尽可能简化,C组同学在问题(1)中引入了非负项y2i,给出了如下与问题(1)等价的等式约束优化问题:
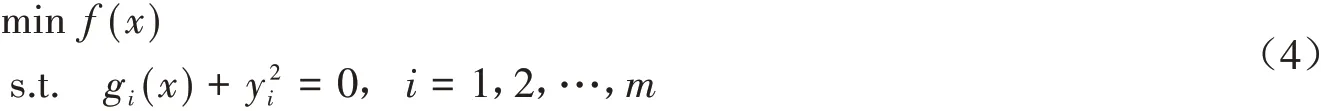
C组同学给出的问题(4)是正确的.本以为学生的讨论会到此结束,没想到C组同学话音刚落,D组同学就给出问题(1)的另一个等价约束优化问题形式.该问题可表示为:

听了C组和D组同学的回答之后,E组同学提出了一个新问题,即问题(4)和问题(5)都是问题(1)的等价约束优化问题形式,那么它们中哪一个应用起来更方便呢?对于这个问题,E组同学指出问题(4)具有更好的数学表示形式,因为二次函数y2i在R1上处处连续可导,而绝对值函数||yi在R1上虽是处处连续,但不是处处可导.
通过引入这种以学生为中心的参与式、讨论式教学方法,不仅加深了学生对最优化基本知识和方法的理解,而且拓展了学生主动探索和研究问题的思路,提高了学生研究问题和解决问题的能力.
1.2 构建最优化知识框架
改变长期以来教师按照章节讲授研究生课程的状况,在《最优化理论与方法》课程教学过程中引导学生建立最优化概念、理论和方法间的脉络和联系,构建起最优化知识间相互关系的框架结构,实现课程内部相关知识点的融会贯通.设计性的课程教学环节要让研究生也参与进来.比如在讲无约束最优化问题

的最速下降法、牛顿法、拟牛顿法、共轭方向法和共轭梯度法等求解方法时,我们知道这些优化算法都是在如下基本迭代下降算法的框架下给出的.
算法1:(基本迭代下降算法)
1.给定初始点x(0)∈Rn,解精度ε>0,令迭代次数k=0.
2.如果迭代点x(k)满足算法的终止条件(与ε有关),则停止迭代;否则转步3.
3.计算下降方向d(k)∈Rn.
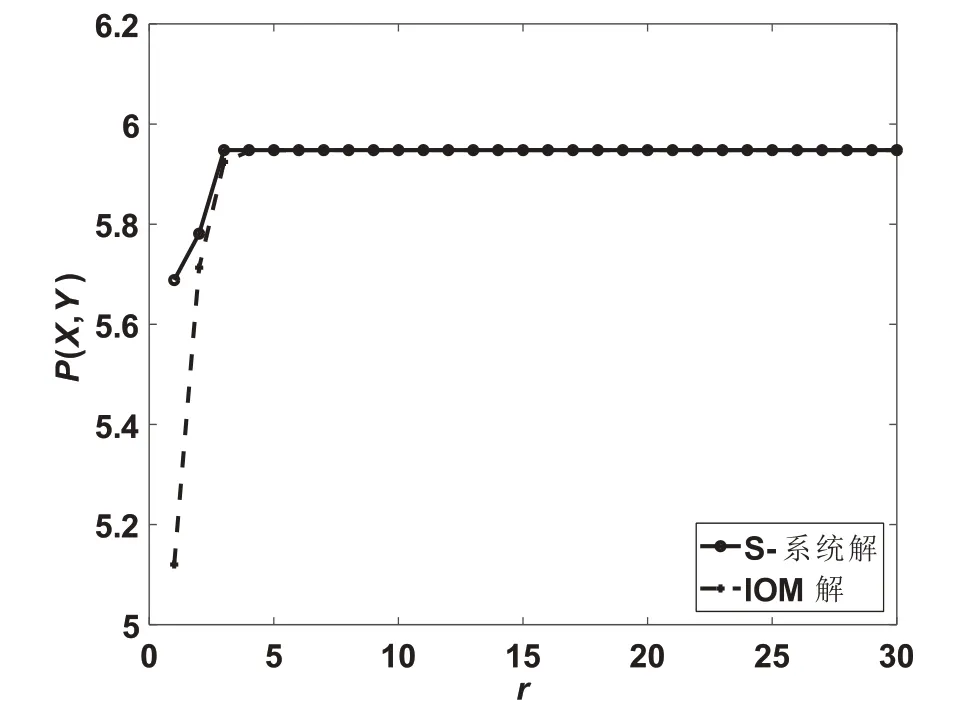
4.确定步长α(k)>0,使得f(x(k)+α(k)d(k)) 5.令x(k+1)=x(k)+α(k)d(k),k=k+1,转步2. 在上述基本迭代下降算法中,给定下降方向d(k)∈Rn就可以得到一个无约束最优化算法.比如令d(k)为最速下降方向-∇f(x(k)),即可得最速下降算法的计算流程.表1给出了当d(k)取不同下降方向时的无约束最优化方法. 表1 基本迭代下降算法框架下的无约束最优化方法 构建这种知识框架结构,有利于学生进一步理解和掌握最优化理论与方法. 《最优化理论与方法》课程与数学建模、数学分析、高等代数、计算方法、计算机软件等课程关系密切,并且《最优化理论与方法》可以应用到生物、化工、经济、管理、人工智能等很多学科中,因此在课程教学中,结合教学内容开展《最优化理论与方法》课程到多学科的知识交叉和拓展是非常必要的.通过这种多学科之间的知识交叉和拓展,可以使研究生得到不同学科知识间自然融会的综合性教学训练.例如在给学生讲授“线性规划解的概念”时,教师可以设计如下问题供学生讨论. 例2[6]:为什么可以 为例叙述线性规划解的概念?其中,x∈Rn,c∈Rn,A∈Rm×n,b∈Rm,b≥0. 例3[6]:不失一般性,是否可以假设A行满秩,即rank(A)=m? 例4[6]:如果rank(A)=m,是否可以假设A的前m列线性无关? 例2很简单,因为任意形式的线性规划问题均可以表示成如问题(6)所示的标准形式. 对于例3,由高等代数知识可知,若rank(A)=r,且r 对于例4,令A=(a1,a2,…,an),aj∈Rm(j=1,2,…,n).由高等代数知识可知,如果rank(A)=m,那么在A的列向量中一定能找到m个ajk,k=1,2,…,m,jk∈I,I={1,2,…,n},使得aj1,aj2,…,ajm线性无关.令A中余下的列向量为ajl,l=m+1,m+2,…,n,jl∈I,jl≠jk.记 容易证明,Cy=b与Ax=b同解,所以原问题(6)等价于如下标准线性规划问题: 因为rank(C)=rank(A)=m,且C的前m列线性无关,故不失一般性,可以假设A的前m列线性无关. 教师在《最优化理论与方法》研究生课程中应该引入用计算机软件求解最优化问题的教学.具体做法是,教师先讲授用计算机软件求解最优化问题的使用方法,然后向学生布置一定数量的数学实验类大作业.通过实际编程求解,学生不仅学会了计算机软件的使用方法,还提高了创新实践能力.笔者在《最优化理论与方法》研究生课程教学中主要讲授如何应用MATLAB软件求解最优化问题.比如应用MATLAB可以求解如下两个问题. 例5:用MATLAB求解问题[7]: 例5的程序代码如图1所示. 图1 例5的程序代码截图 运行程序可以得到例5的最优解为x*=(19.785,0,3.32,11.385,2.57)T,f*=89.575. 例6:用MATLAB求解问题: 例6的程序代码如图2所示. 图2 例6的程序代码截图 运行程序可以得到例6的最优解为x*=(0.7079,-0.0354)T,f*=-867.5519. 在《最优化理论与方法》研究生课程教学中,教师应该鼓励学生主动进行一些专题研究,选题可以是某些最优化理论与方法的优缺点,也可以是学生自己感兴趣的问题.学生选题后会查阅相关文献资料,并提出自己的想法开展最优化理论与应用研究,以总结报告或撰写论文的形式汇报自己的研究成果,从而锻炼了研究生提出问题、探索问题和解决问题的能力.比如在学习完最速下降法和牛顿法以后,有的同学发现最速下降法具有对初始点无特别要求、后期收敛缓慢等特点,而牛顿法则收敛速度快,但对初始点的要求比较高,于是基于最速下降法和牛顿法提出了一种混合优化算法.再比如有的同学将约束优化问题的最优性条件和罚函数法的思想应用于双层规划问题的求解.这些探索研究性工作不仅加深了学生对最优化理论与方法的学习和理解,还具有一定的创新性,有利于提高研究生的创新性思维. 案例教学是激励应用数学、运筹学与控制论专业研究生采用最优化理论和方法解决应用问题的重要途径.这就要求教师在教学中除讲授经典的最优化理论和方法外,还应该不断提高业务素质,以适应新时代应用中对最优化技术迫切需求的教学工作要求.教师在《最优化理论与方法》教学中,应该引入一些应用最优化方法解决实际问题的案例,从而提高学生解决实际问题的能力.以下为笔者在《最优化理论与方法》教学中所采用的应用优化案例. 例7:生物化学系统的稳态优化[8-11].针对生物化学系统 构建如下稳态优化问题: 其中,X∈Rn(X>0)为代谢物浓度向量,Y∈Rm(Y>0)为参数向量,P为产物产率,F∈Rn,XL∈Rn(XL>0),XU∈Rn,YL∈Rm(YL>0),YU∈Rm,G∈Rp. 应用如下迭代线性优化算法[8-10]可以求解非线性问题(8),具体算法推导及符号意义可以参见文献[8-10]. 算法2:(迭代线性优化算法) 2.对给定的Y(r),由式(7)求出X(r)(IOM解);将式(7)和P(X,Y)化为S-系统形式. 3.对S-系统进行质量评估.若S-系统稳定且鲁棒,则转步4;否则转步2修正Y(r). 4.对w=w(r),c=c(r)和λ(w,c)=λ(w(r),c(r)),求解问题(9). 5.若同时成立 则停止迭代;否则转步6. 6.更新Y,η1,η2和η3: 令r=r+1,转步2. 将算法2应用于色氨酸生物合成系统[8-10]中,最优色氨酸产率计算结果如图3所示. 图3 最优色氨酸产率迭代计算结果 通过以上创新性思维在《最优化理论与方法》课程教学中的教学方法改革与实践,调动了研究生自主学习、掌握最优化基本理论与方法的学习热情和兴趣,有利于学生自主学习、主动探索、发现问题、解决问题、科学研究、科技创新等能力的提高,从而提升研究生人才培养效果.因此,基于创新性思维的《最优化理论与方法》课程教学改革与实践对研究生教学质量和效果的提高具有重要的意义.
1.3 多学科的知识交叉和拓展

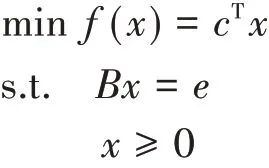
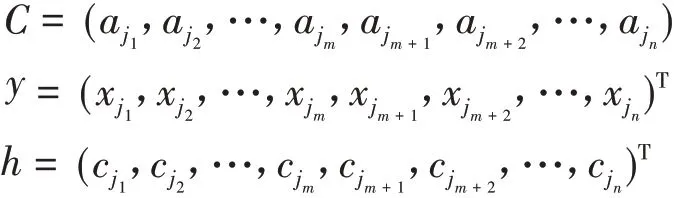
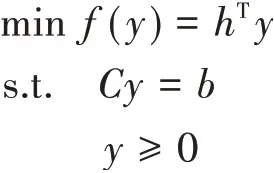
1.4 布置数学实验类大作业,实现理论学习到实践能力的转化



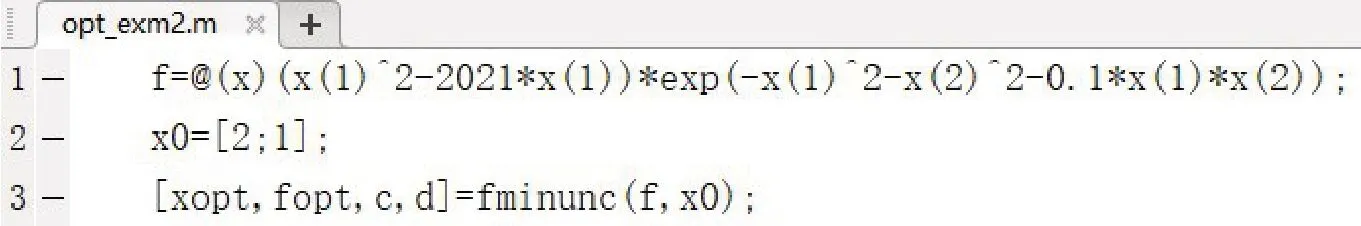
1.5 鼓励研究生从单纯的课程学习向有创新性的探索转变
1.6 开展应用案例教学,实现理论学习到实际应用的转化


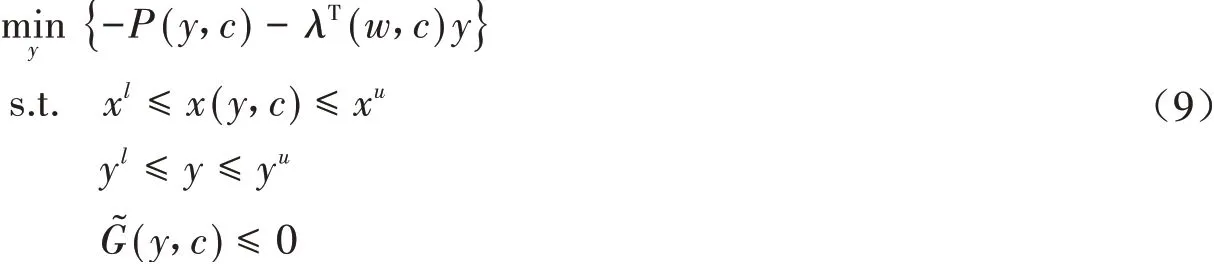

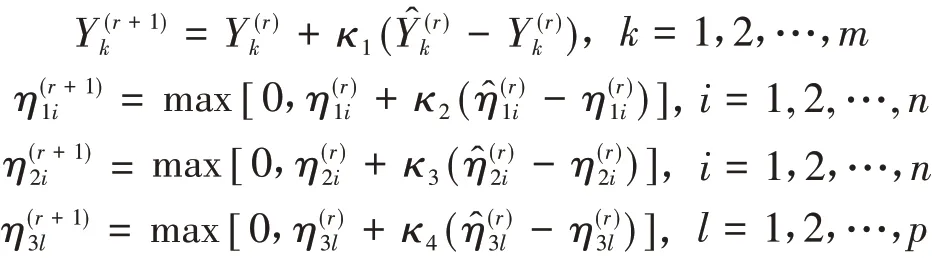
2 结论

