Quantum speed limit for the maximum coherent state under the squeezed environment∗

Kang-Ying Du(杜康英),Ya-Jie Ma(马雅洁),Shao-Xiong Wu(武少雄),†,and Chang-Shui Yu(于长水)

1School of Science,North University of China,Taiyuan 030051,China

2School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords:quantum speed limit,squeezed reservoir,Jaynes–Cummings model,dephasing model

1.Introduction

In the quantum information processing,the evolution of quantum system is of great significance.One may ask what is the minimum time for a quantum state evolute to another state?Mandelstam and Tamm(MT)investigated a pure state evolve to its orthogonal state,and found that the shortest time is related to the variance of energy,i.e.,π¯h/2ΔE,which can be considered as an extension form of Heisenberg time–energy relation,and is called the MT bound.[1]The shortest time is known as the quantum speed limit time.Under the energy representation,Margolus and Levitin(ML)reinvestigated the transition probability amplitude question between two orthogonal quantum pure states,and found that the minimum time is related to the mean value of energy,i.e.,π¯h/2〈E〉,which is called ML bound.[2]In order to describe the evolution of quantum state more efficiently,the unified form of quantum speed limit time is given by

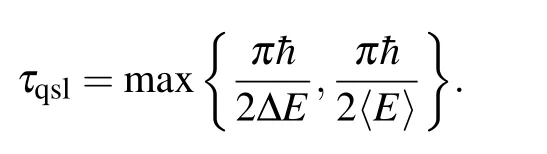
The evolution of closed system is investigated in diverse ways from the perspective of quantum speed limit.[3–12]

With the booming development of quantum information field,the theory of open quantum systems is employed to deal with the dynamical evolution of quantum systems.[13,14]Naturely,the concept of quantum speed limit is extended to open quantum systems,and investigated in different ways,such as the quantum Fisher information,[15]or the relative purity.[16]In Ref.[17],a unified form of quantum speed limit time for open quantum systems is proposed by utilizing the von Neumann trace inequality and Cauchy–Schwarz inequality for operators.Inspired by these results,the properties of quantum speed limit for open systems have been reported for both initial pure and mixed states under various distances.[18–32]The other aspects of quantum speed limit time were also considered,such as the relationship with the information theory[33,34]or the quantum control,[35–41]the non-Hermite quantum system,[42]the experimental demonstration.[43]One can see the comprehensive reviews[44,45]to get more information about the quantum speed limit for open systems.The speed limit in phase space has also been reported.[46–52]

The squeezed environment is an important physical resource for quantum information processing,[53–55]it can be used to enhance the parameter estimation,such as the precision of gravitational wave detection.[56,57]If the environment interacting with the quantum system is squeezed reservoir,how does the squeezed parameters affect the quantum speed limit for open systems?In this paper,we will investigate the properties of quantum speed limit with squeezed reservoir.Two pedagogical models,the damped Jaynes–Cummings model and the dephasing model,are investigated.Without loss of generality,the initial state is assumed as maximal coherent state.For the damped Jaynes–Cummings model under squeezed environment,the quantum speed limit time indicates symmetrical distribution about the phase parametersθ,and the quantum speed limit bound will be sharper along with the increase of squeezed parameter r.In addition,the quantum speed limit time can also be affected by the coupling strength between the quantum system and surrounding environment.In the dephasing model under squeezed environment,the quantum speed limit time is only determined by the dephasing rate,and the acceleration boundary can be broken compared to the case that interacting with vacuum reservoir for appropriate squeezed parameters.

2.The unifed form of quantum speed limit for open quantum systems

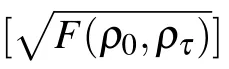
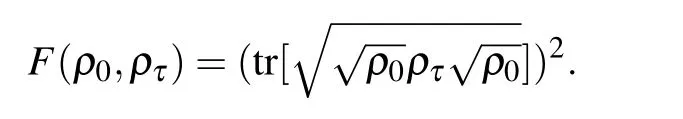
Through this geometric distance,a unified form of quantum speed limit time for open systems with time-dependent nonunitary dynamical operator Lt(ρt)can be obtained by following Ref.[17].

Employing the von Neumann trace inequality for operators,the ML-type quantum speed limit time for open quantum systems is given as

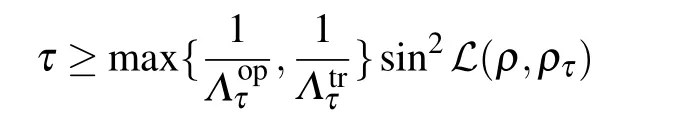
with the quantum evolution rate

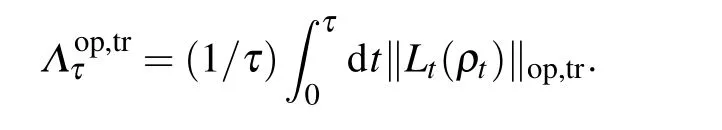
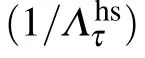
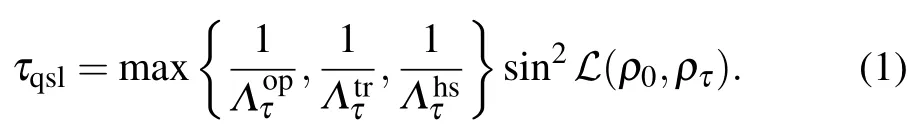
Due to the norms of matrix satisfy the inequality‖·‖op≤‖·‖hs≤‖·‖tr,the ML-type bound of quantum speed limit based on operator norm is tight for open quantum systems.In the following,we will apply the formula(1)to the squeezed environment for the damped Jaynes–Cummings model and dephasing model,and investigate the effect of squeezed environment parameters on the properties of quantum speed limit.

3.The quantum speed limit for damped Jaynes–Cummings model

In this section,we will consider the quantum speed limit time for damped Jaynes–Cummings model under squeezed environment.The total Hamiltonian of quantum system and squeezed environment is H=Hs+Henv+Hintwith

The environment is assumed as squeezed vacuum reservoir

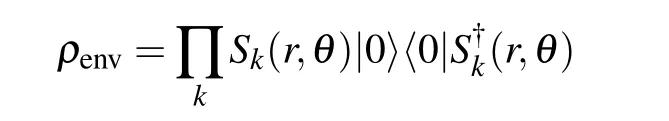
with the unitary squeeze operator

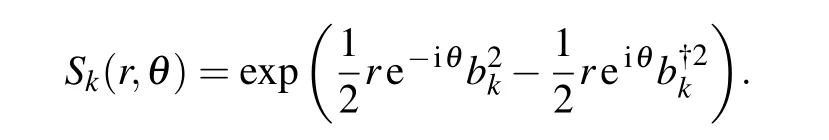
Following Refs.[58–60],the non-perturbative master equation through path integral method is given by

with the super operators

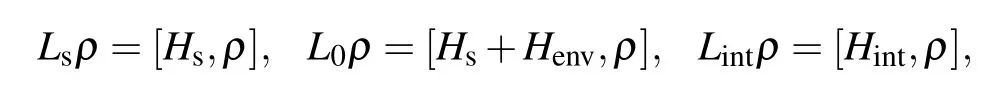
and has the following form:[58]

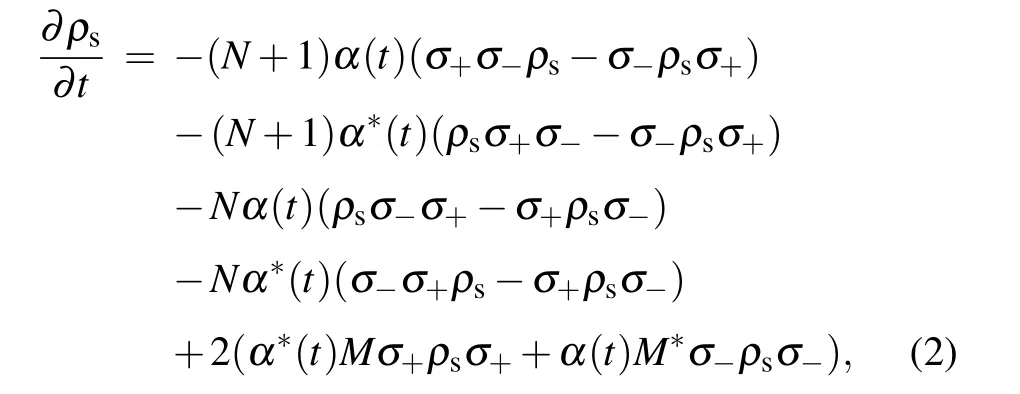
where N=sinh2r,M=−coshrsinhreiθare given in terms of squeezed parameter r and phase parameterθ.

The structure of squeezed environment interacting with the quantum system is assumed as Lorentz form

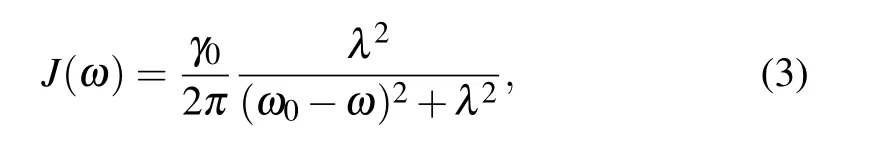
where the spectral widthλis related to correlation time,and coupling strengthγ0is determined by the relaxation time.

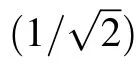
where the elements of density matrix(4)are given by

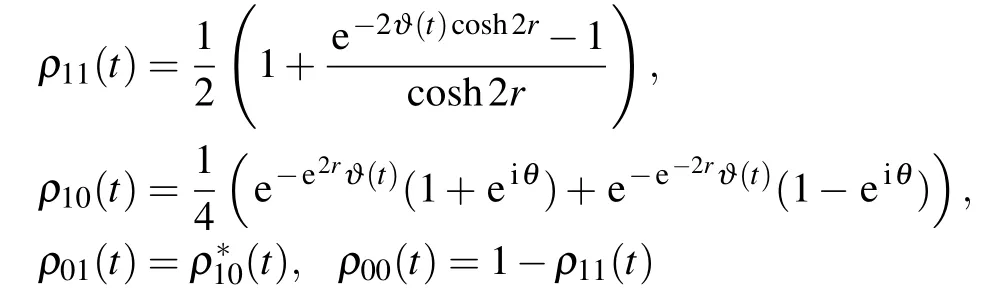
with the parameters

The ML-type quantum speed limit time based on operator norm is

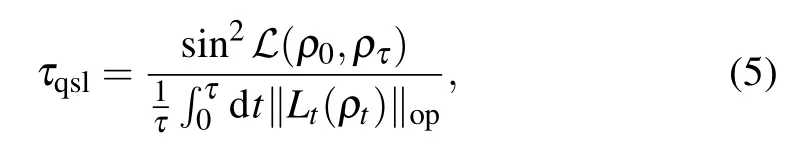
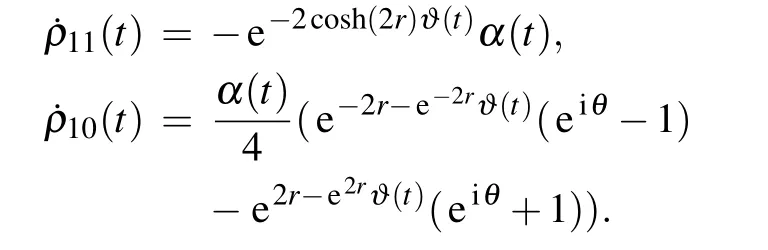
In Fig.1,the behavior of ratioτqsl/τwith squeezed environment parameters r andθare shown,respectively.In both panels,the environment spectral width is set asλ=1(in units ofω0)and the actual driving time is chosen asτ=1.In panel(a),it is shown that the variation of quantum speed limit time along with the coupling strengthγ0and phase parameter θ.The squeezed parameter is chosen as r=0.5 and the quantum speed limit time shows symmetry about the phase parameter valueθ=π.The ML-type quantum speed limit time(5)is only comprised of the phase parameterθwith form eiθand its complex conjugate,so it presents periodic characteristics,obviously.When other parameters are fixed,the maximum of quantum speed limit time is located atθ=0.It indicates that the appropriate phases parameterθcan accelerate the evolution of quantum states under squeezed environment.

Even though without Markovian approximation used in non-perturbative master equation(2),the variation of environment coupling strengthγ0does not reflect the phenomenon of non-Markovianity for open quantum systems.[13,14]It maybe caused by different methods to deal with the master equation.However,the quantum speed limit time will be larger along with the coupling strengthγ0increasing,which is distinguished with the result in Ref.[17]even when the squeezing effect is vanished.

Fig.1.The function ofτqsl/τfor damped Jaynes-Cummings model under squeezed environment.In panel(a),the ratioτqsl/τis varied along with the phase parameterθand coupling strengthγ0.The squeezed parameter is chosen as r=0.5.In panel(b),it shows the variation ofτqsl/τalong with the squeezed parameter r and coupling strengthγ0.The phase parameter is chosen asθ=0.5π.In both panels,the spectral width is set asλ=1(in units ofω0)and the actual driving time is chosen asτ=1.

4.The quantum speed limit for dephasing model

In this section,we will consider another pedagogical model,the dephasing model,and assume the environment interacting with quantum system is squeezed vacuum state,the total Hamiltonian of quantum system and environment is

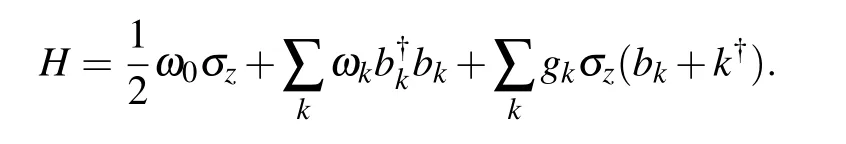
where the dephasing factorγ(t)is defined by

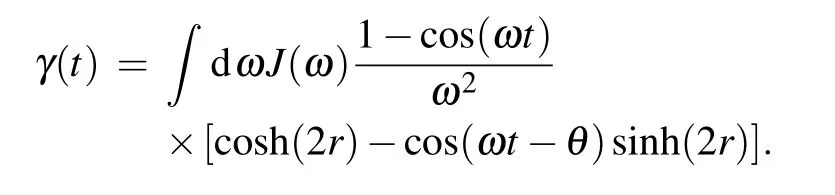
Without loss of generality,the structure of environment is Ohmic-like spectrum with soft cutoff

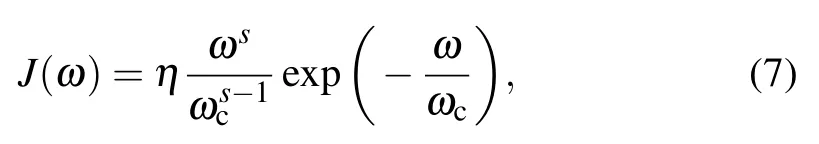
whereηis the coupling parameter,the cutoff frequencyωcis unity,and s determines the type of environment,i.e.,sub-Ohmic environment(s<1),Ohmic environment(s=1),and super-Ohmic environment(s>1),respectively.The dephasing factorγ(t)in Eq.(6)can be given analytically[61]

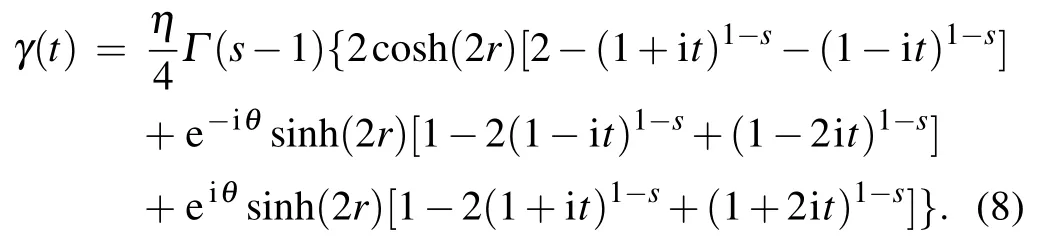
The ML-type quantum speed limit time based on operator norm for dephasing model under squeezed environment can be given as follows:

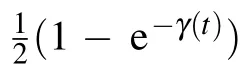
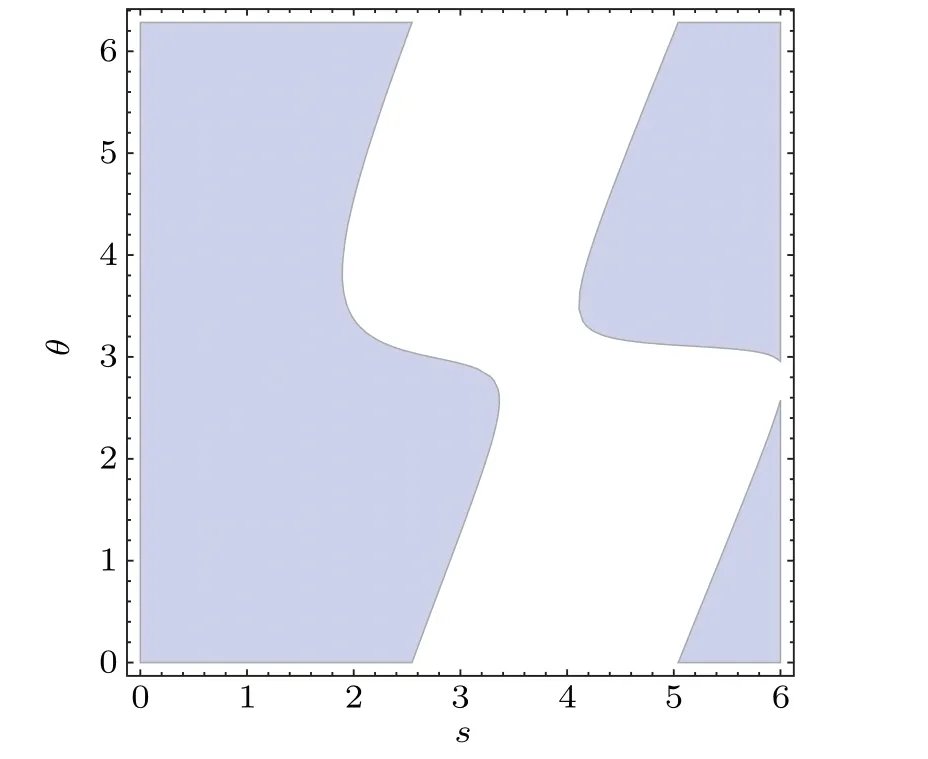
Fig.2.The sign of dephasing rateγ′(t)in Eq.(10).The purple region means γ′(t)>0 and the white region isγ′(t)<0.The horizontal axis is Ohmic spectrum parameter s and the vertical axis is phase parameterθ.The squeezed parameter r is set as 1,and the actual driven time is chosen asτ=3.

5.Discussion and conclusion

We have investigated the quantum speed limit for open quantum system under squeezed environment.Two typical models,i.e.,the damped Jaynes–Cummings model and the dephasing model,are considered,and the initial states are chosen as maximal coherent state for both models.For the damped Jaynes–Cummings model,the quantum speed limit time is larger along with the squeezed parameter r increasing and shows symmetry about the phase parameterθ.While,for the dephasing model,the quantum speed limit time is determined by the dephasing rateγ′(t)and the acceleration boundary that interacting with vacuum reservoir can be broken under the squeezed reservoir for appropriate squeezed parameters.We expect that our research has contribution to understand the evolution of quantum states in squeezed environments.