Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile∗
Xiao-Feng Shi(石晓峰),Dong-Jun Ma(马东军),†,Zong-Qiang Ma(马宗强),De-Jun Sun(孙德军),and Pei Wang(王裴),2,‡
1Institute of Applied Physical and Computational Mathematics,Beijing 100094,China
2Center for Applied Physics and Technology,Peking University,Beijing 100871,China
3Department of Modern Mechanics,University of Science and Technology of China,Hefei 230027,China
Keywords:bifurcation and continuation,symmetry-breaking,hysteresis,surface driven cavity flow
1.Introduction
The incompressible shear-driven flow inside a finite wallbounded cavity has been a typical hydrodynamic problem with rich nonlinear dynamics from stationary to time periodic and chaotic.[1–3]It has wide practical applications such as the built-in warehouse of fighter aircraft and the flow of lakes and oceans driven by wind.[4,5]Furthermore,it is a general benchmark example to verify the accuracy of numerical methods for the incompressible flow.[6]Although the geometry of the shear-driven cavity is simple,it contains complex nonlinear flow phenomena,and its flow stability and bifurcation behavior have been extensively studied.[1,2,7–10]
The nonlinear dynamics and bifurcation of lid-driven cavity flows have been investigated with various numerical methods.[11]The simulations of full time-dependent Navier–Stokes equations can capture the stable bifurcation procedures from initial stationary state to time periodic oscillations and chaotic patterns.[12,13]The first two-dimensional instability of lid-driven square cavity flow is a supercritical Hopf bifurcation,and its exact occurrence in parameter space is extremely dependent on both resolution and the way by which the corner singularity is treated.When the Reynolds number exceeds about 7800,the steady flow field bifurcates to an oscillating periodic solution.When the Reynolds number exceeds 11000 or more,the chaotic state will appear.[7]
The driving speed of the lid cover has important influences on the cavity flows and determines the nonlinear flow patterns.[2,4,5]In the flow of lakes and oceans driven by wind,the wind is usually non-uniform over the surface of lakes and oceans.Zeccheto and de Biasio indicted that the average wind changes direction approximately 180°along the basin in Alboran Sea.[14]To simulate such a driving condition,this paper focuses on the square cavity flow driven by a lid cover with antisymmetric sinusoidal velocity profile,which does not have the singularity of velocity boundary conditions near the corners,and is more suitable to be a general benchmark problem for computational fluid dynamics.Furthermore,the symmetric driven square cavity flow contains more nonlinear dynamic phenomena,such as symmetry breaking,coexistence of multiple steady solutions,hysteresis,and subcritical Hopf bifurcation.For such a complex flow problem,it is difficult to obtain the unstable steady solutions and quantitative bifurcation processes only by the direct numerical simulation.[15,16]
The numerical modelling and analysis of bifurcation problems in fluid mechanics has been extensively discussed in literature,[15,17–20]where the numerical analysis of bifurcation problems in the incompressible fluid mechanics was discussed and the convergence theory for several important bifurcations was described for the projection-type,finite difference and mixed finite element methods.Generally,there are three sequential parts in the computational approach.[19]First a discrete representation of the model equations has to be obtained through some kind of discretization procedure.[17]The second part is to apply specific techniques of numerical bifurcation theory[15,18]to track the solution branches.The third part of the computational work is to access the linear stability of the solution state.Following this idea,Tuckerman et al.[15,20,21]have proposed a global instability analyzing methodology,by which an explicit-implicit time integration code could be easily transformed to carry out for steady-state solving,bifurcation points,continuation,linear stability analysis,and nonlinear transient growth analysis in fluid mechanics.Here,we use this methodology[16,22–26]of nonlinear global stability and bifurcation theory to solve the multiple solutions and hysteresis in the symmetric driven square cavity flow.
Farias and McHugh used the lattice Boltzmann(LB)method to study the cavity flow with the same configuration and found two stable coexisting solutions.[4]Due to the limitation of research tools,they only gave qualitative intervals of the flow patterns and cannot capture the unstable solutions.Some important physical phenomena may be omitted.In this paper,the problem is studied from the view of nonlinear bifurcation,and the coexistence of multiple solutions is discussed for the Navier–Stokes equations at Re<2500.With a numerical continuation,all of the stable and unstable steady solutions are solved out,and the complete bifurcation curve with critical parameters for these flow patterns are presented.
2.Numerical methods
Considering the two-dimensional unsteady incompressible flow where both the density and viscosity of the fluid are constant,the governing equations are the Navier–Stokes equations
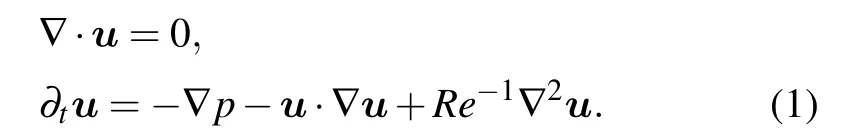
A high-order spectral/hp element method[26,27]with a domain decomposition Stokes solver is utilized to solve the governing Eq.(1).The computation domain is decomposed into non-overlapping structured or unstructured spectral elements.Within each element Gauss–Lobatto–Jacobi and Gauss-Radau-Jacobi quadrature points are used in two directions respectively in order to guarantee the integration conditions.The second-order stiff stable scheme is adopted for the unsteady time integration.The linear terms are treated implicitly and the nonlinear terms explicitly.Then the discretized equations can be re-formed with an unsteady Stokes operator on the left-hand side and explicit forcing terms on the right-hand side.[15]With the domain decomposition approach,the interior and marginal degrees of freedom are decoupled and the incompressible divergence-free condition is satisfied strictly.The resulting small linear system in each element can be solved by direct method.
The governing equations can be re-formed as

where N and L represent the nonlinear and linear operators,respectively.For semi-implicit scheme we have

The steady-state solution for the Navier–Stokes equations with variables(u,Re)reads

Applying Newton’s method to Eq.(4),the linear equation for the correctionδu is(Nu+L)δu=−(N+L)u where Nuis the Jocabian matrix associated with the nonlinear term N evaluated at state u.Following Tuckerman’s idea,[15]a Jacobian-free Newton–Krylov method[22,26]is used to obtain stable or unstable steady solutions.Using the Stokes operator P=(I−ΔtL)−1Δt as a preconditioner,the linear system can be reformulated as
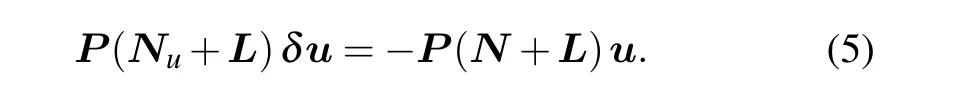
Inexact Newton iteration is used for accelerating convergence,where the right-and left-hand sides of Eq.(5)are calculated by a time-stepping based on Eq.(3).
In order to follow the bifurcation path of the dynamic system,a pseudo-arclength numerical continuation[17,19,28]is used to avoid the difficulty due to the turning point.The extended linear system based on the vector(u,Re)is
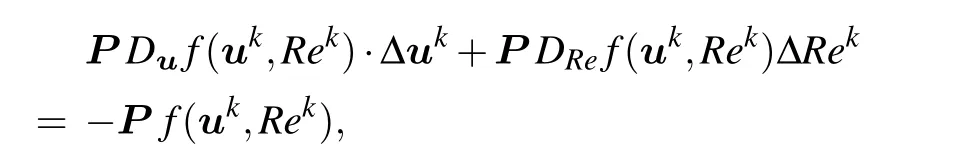
where Duand DReare the linearized operators for variables u and Re,respectively.This system is solved by a Jacobian-free Newton–Krylov method with a Householder transformation.[29]
An iterative Arnoldi method is utilized to calculate the leading eigenvalues and their corresponding eigenvectors for the system.The detailed implementation can refer to the published papers.[16,22–26]
The laminar flow past a stationary cylinder between two parallel plates is analyzed to verify the accuracy of the proposed method.Similar to lid-driven cavity flow,this flow also contains the vortexes,symmetrical crushing and supercritical Hopf bifurcation.Cliffe et al.showed that the flow will lose stability to a periodic flow at a supercritical Hopf bifurcation point as the flow rate is increased,and there is another Hopf bifurcation to re-stabilize the flow above a critical Reynolds number.[30]Furthermore,steady asymmetric flows exist at the same blockage ratio B(the ratio of cylindrical diameter to plate width).We performed the bifurcation analysis at the special blockage ratio B=0.7,where steady symmetric solutions,steady asymmetric solutions and periodic solutions can be obtained,and the critical Reynolds and Strouhal numbers are given in Table 1.The computational region is divided into 130 iso-parametric quadrilateral elements,each of which has an interpolation order of p=11.Table 1 shows the comparisons between the results of the present high-order spectral element method and those of finite element method.[30]The critical parameters agree well with the first two Hopf bifurcations.This agreement verifies the ability of the present numerical method to describe the flow bifurcation.Figure 1 shows the streamlines of different symmetric and asymmetric steady solutions near the critical bifurcation points.

Table 1.Critical Reynolds and Strouhal numbers for blocked cylinder flow(B=0.7).

Fig.1.Streamline for blockage ration B=0.7:(a)Re=90,(b)Re=175,(c)Re=185.
3.Results and discussion
The computational zone is set as a unit square cavity[0,1]×[0,1],as shown in Fig.2.The lid cover has an antisymmetric sinusoidal velocity boundary condition u(x)=sin(2πx),and the other three sides are set as fixed wall.The whole system is symmetric about the vertical central line,and there exists a basic symmetric numerical solution.Because of the simplicity of geometry,a spectral element method with 60 discrete points in each direction is adopted.The symmetric streamlines at Re=100 are demonstrated in Fig.3.Driven by the antisymmetric sinusoidal velocity,two main vortices are formed in the square cavity,and there are two secondary vortices at the corners.When the Re number increases,the symmetric solution may convert to be unstable or asymmetric.In order to characterize the final state of flow field,a symmetry parameter(integral of the absolute value of horizontal velocity along the centerline)is considered,


Fig.2.Schematic diagram of cavity flow driven by lid cover with sinusoidal velocity profile.

Fig.3.Streamlines for symmetric flow at Re=100.
Farias and McHugh gave one bifurcation curve of the flow,[4]indicated that there is a subcritical bifurcation with symmetry breaking.When the Re number is less than the critical Rec,only one stable symmetric solution with two principal vortices exists;when the Re number is larger than Rec,there will be multiple stable solutions,and only stable asymmetric solutions were shown in the paper of Farias and McHugh.
3.1.Bifurcation of asymmetric solutions
The bifurcation curve of asymmetric solutions calculated in this paper is given in Fig.4 when Re<2500.The symmetric solutions are stable in the range of Reynolds number,which are not given in the figure.Periodic oscillations occur when Re is around 2500,but only the cases of steady solutions are considered here.The pseudo-arclength numerical continuation technique is used to follow all the solution branches including bifurcation and turning points.At the beginning,the initial symmetric solution at Re=100 was obtained by time integration,and the symmetric solution at Re=500 was calculated by the Newton method.Then a small asymmetric perturbation was added to the symmetric Re=500 solution,and the asymmetric stable solution could be obtained by unsteady time integration method.Therefore,we made the switch from the symmetric branch to the asymmetric stable branch.All the steady solutions then could be followed by the continuation method through increasing or decreasing the Reynolds number.Three turning points on the asymmetric branch were captured by the pseudo-arclength technique.The stable or unstable properties of these branch states have to be determined by linear stability analysis or verified by unsteady time integration where the unstable solution would be divergence.
Figure 4(a)shows all branches of the asymmetric solutions,and Fig.4(b)gives the enlarged display of the hysteresis curve in Fig.4(a).There are three turning points TP1(Re≃320),TP2(Re≃2208)and TP3(Re≃2262).The bifurcation curve is divided into four branches by these three turning points:(1)left branch(TP1 to TP3,320≤Re≤2262);(2)right branch(TP2 to right end,Re≥2208);(3)down branch(below TP1,Re≥320);(4)hysteretic branch(TP3 to TP2,2208≤Re≤2262).
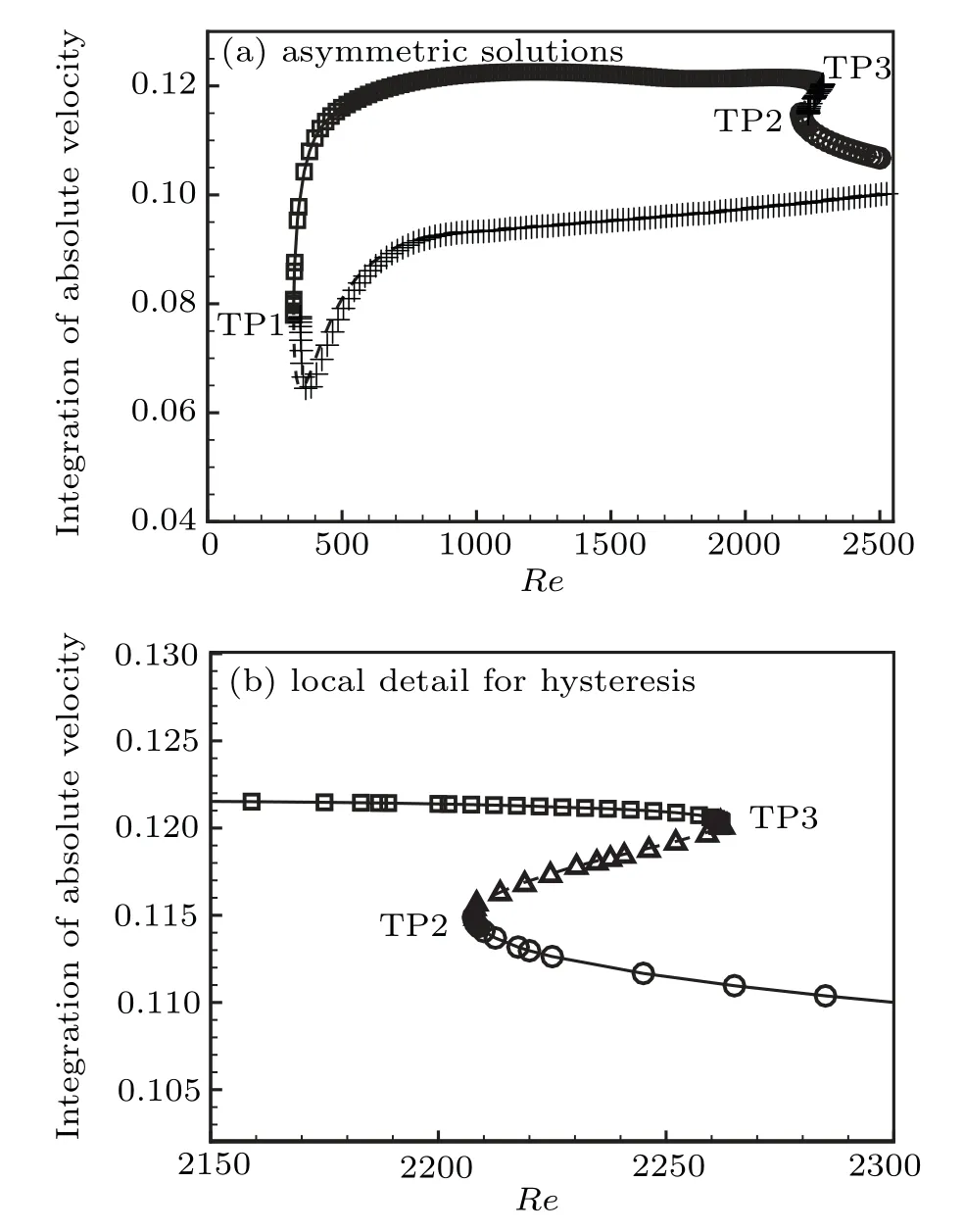
Fig.4.Bifurcation curve for symmetric driven square cavity flow.The asymmetric solutions:(1)square:stable solutions,left branch;(2)circle:stable solutions,right branch;(3)cross:unstable solution,down branch;(4)triangle:unstable solution,hysteretic branch.
In these four branches,the left and right branches are stable,which are represented by squares and circles in Fig.4,respectively,whereas the down and hysteretic branches are unstable,which are represented by cross and triangle symbols.In the Reynolds number range(320,2208)and(2262,2500),there are one stable and one unstable asymmetric flow patterns.In the Reynolds number range(2208,2262),the pair number of stable and unstable asymmetric solutions changes to be two simultaneously.
3.2.Multiple solutions at the same Reynolds number
Firstly,we discuss the cases of simple multiple solutions(Re in(320,2208)or(2262,2500)).Subcritical bifurcation with broken symmetry can easily lead to the coexistence of multiple solutions under the same Re number.According to the bifurcation theory of dynamical system,there must be at least one unstable steady solution between the stable symmetric and asymmetric flow patterns.In Refs.[4,5],it was difficult to obtain unstable steady solutions by the explicit time marching method,so that the corresponding flow patterns could not be obtained.Figure 5 shows the present results of streamlines at Re=330,1000,1500,including the stable symmetric and asymmetric solutions,and the corresponding unstable asymmetric solutions.The mirror images of the asymmetric solutions are omitted here.
Near the turning point,such as Re=330,the asymmetric solutions have just appeared,and the stable and unstable asymmetric flow patterns are similar.They are the structures of one pair of primary vortices in the cavity center and the secondary vortices in the corners.When Re=1000,the cores of the main vortex in these three solutions move downward gradually.In the stable asymmetric pattern,the secondary vortices in the upper right corner become smaller due to the squeezing of the main vortices,while the secondary vortices in the lower left corner become stronger gradually.In the unstable asymmetric pattern,only the lower left secondary vortex has a slight enhancement.When Re=1500,there is no remarkable change of the main vortices in the three solutions,expect some flow separations and small vortices appear on the side walls in both the symmetric and unstable asymmetric solutions.These flow separations begin to appear on the side wall around Re=1090,which leads to the bifurcation of the flow topology.However,according to the bifurcation curve and stability analysis,there is no bifurcation of the solutions of Navier–Stokes equations.
In order to verify the correctness of the results presented here,both the steady SIMPLE method and the stream function method[31]are used to simulate this problem.Because the SIMPLE method does not adopt Newton iteration,it is difficult to converge to the unstable asymmetric solution.However,the stream function method with inexact Newton algorithm can obtain the unstable solution,and the results are in good agreement with those obtained by the present spectral element method.In order to verify the stability of the flow states,unsteady computations are carried out for the evolution of each steady solution with small perturbations.The perturbations of the stable steady states will gradually decay and the states converge to the original solutions,whereas the perturbations of the unstable steady states will continue to increase and eventually the states converge to one of the stable branches,which is consistent with the linear stability analysis.

Fig.5.Streamlines for symmetric,asymmetric stable and asymmetric unstable solutions of cavity flow at Re=330,1000,1500.
3.3.Hysteresis for asymmetric solutions
In addition to the multiple coexisting solutions,there is a novel hysteresis phenomenon in the range of 2208 The typical solutions in the hysteresis at Re=2230 are given in Fig.6.The flow patterns of these symmetric and asymmetric solutions are similar to those at Re=1500,except that the secondary vortices on the corner develop more completely.For the stable asymmetric solutions,a new flow separation appears in the left side wall and generates a new secondary vortex.The wall secondary vortex is separated with the corner secondary vortex by the main vortex in the asymmetric solution of left branch,while these two secondary vortexes contact with each other and are ready to merge in the corresponding right branch.The flow field of the unstable solution in the hysteresis is between these two stable asymmetric states,where the wall and corner secondary vortexes just come into contact with each other.The main difference between the solutions of the left and right branches is the relationship of secondary vortices near the wall and corner.The growth competition and merger of these two secondary vortices result in the hysteresis phenomenon.The down branch is always alone,so its solution has a remarkable difference with the other asymmetric solutions. Fig.6.Streamlines for multiple coexisting solutions of cavity flow at Re=2230 in the hysteresis. In this paper,the steady flow in a square cavity driven by a lid cover with antisymmetric sinusoidal velocity profile is numerically studied.By the bifurcation analysis and numerical continuation,the coexistence of multiple solutions of the Navier–Stokes equations at Re<2500 is obtained.The new bifurcation curve of symmetric and asymmetric steady states are presented,and the corresponding flow patterns are discussed.The critical Re number of asymmetric solutions is found to be 320.The stable symmetric and asymmetric solutions are consistent with those in literature,and a new set of unstable asymmetric solutions are obtained.When Re<320,there is only one stable symmetric solution for the flow;when 320
4.Conclusion

