An improved model of damage depth of shock-melted metal in microspall under triangular wave loading∗
Wen-Bin Liu(刘文斌),An-Min He(何安民),Kun Wang(王昆),Jian-Ting Xin(辛建婷),Jian-Li Shao(邵建立),Nan-Sheng Liu(刘难生),and Pei Wang(王裴),,7,†
1Department of Modern Mechanics,University of Science and Technology of China,Hefei 230027,China
2Institute of Applied Physics and Computational Mathematics,Beijing 100094,China
3Graduate School of China Academy of Engineering Physics,Beijing 100088,China
4College of Materials Science and Engineering,Hunan University,Changsha 410082,China
5Science and Technology on Plasma Physics Laboratory,Research Center of Laser Fusion,China Academy of Engineering Physics,Mianyang 621900,China
6State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China
7Center for Applied Physics and Technology,Peking University,Beijing 100871,China
Keywords:damage depth,theoretical modeling,microspall,triangular wave
1.Introduction
When a triangular wave propagating in the material reflects from the free surface,the interaction of the incident rarefaction wave with the reflected rarefaction wave generates tensile stress that may internally damage the material,and this damage can range from small voids or cracks to macroscopic fractures and the ejection of one or several spall layers.[1]If the material is shocked above its melting pressure or melted on release from a lower shock pressure,tensile stress emerges in the melted materials and the dynamic damage process is referred to as“microspall”.[2]Microspall has attracted great attention from scientists and engineers over the past decades because it has been observed in inertial confinement fusion[3–6]and laser-driven surface micromachining.[7–9]
Experimental,theoretical and computational studies of microspall have been carried out over the past decades.Andriot et al.[2]studied the effect of melting on spallation using Doppler laser interferometry and x-ray densitometry.Several features of microspall were reported,including a dramatic decrease in free-surface reflectivity,continuous ejection of material and a significant increase in the number of ejecta.Ress´eguier et al.[5,10]studied the microspall of tin using the time-resolved velocity measurements and post-shock observations of recovered targets and fragments,and they found that the velocity interferometer system for any reflector(VISAR)signal disappeared when the material melts,which is consistent with Andriot’s discovery.Kanel et al.[11]investigated the spall strength of tin and lead,and they found that melting reduces the spall strength of lead and tin by at least an order of magnitude.Chen et al.[4]developed an improved Asay window technique to study the microspall of tin.An analytical method is developed to convert the measured data into the spatial volume density distribution,and the results are in good agreement with those obtained from x-ray radiograph.Theoretically,Kuksin et al.[12]established a spall model for liquids based on a void nucleation and growth approach.The model was applied to the estimation of liquid spall strength,and the result agrees well with experimental data.Xiang et al.[13]developed a model of microspall by coupling dynamic ductile damage and melting.The model was added to the finite element code and simulated spall experiments,and the simulation results are in good agreement with previous experiments.Computationally,molecular dynamics(MD)is an important theoretical tool for studying microspall.Luo et al.[14]investigated spallation in solid and liquid copper at high strain rates.Shao et al.[15,16]studied the failure mechanism and spall strength of single crystal aluminum under triangular wave loadings.Xiang et al.[17,18]studied the effects of shock intensity and loading rise time on the spall behavior of lead.Wang et al.[19]investigated the spall behaviors of melted lead under various triangular waves.However,most of the existing studies are focused on the mechanism of microspall damage,and there are few studies on the damage depth of microspall.Damage depth,the ratio of the damage mass per unit surface area to the density at rest condition,is an important parameter to describe the degree of damage.On the one hand,when a triangular wave reflects from the free surface of the material,the interaction of the incident rarefaction wave with the reflected rarefaction wave generates tensile stress that internally damages the material,where the material changes from continuous material to damaged material,and it is necessary to know the mass of damaged material.On the other hand,the damage depth is closely related to the physical processes such as secondary shock and particle-gas mixing.[20–22]Shao et al.[23]proposed an approximate description of damage depth under triangular wave loading when the material’s compressibility is considered.However,under strong triangular wave loading,the effect of the relative movement is obvious and should also be taken into account when performing theoretical modeling of damage depth.
In order to study the damage depth of shock-melted metal in microspall under triangular wave loading,an improved model of damage depth of shock-melted metal is proposed,taking into account not only the effect of the material’s compressibility,but also the effect of the relative movement.Then,the microspall is investigated in the laser-driven shock loading experiment,and the proposed model is compared with the experiment and the model considering only the effect of the material’s compressibility.[23]Finally,the effects of peak stress and decay length of the incident triangular wave on the damage depth are investigated by SPH simulations.Besides,the applicability of the threshold stress criterion for melted metal at high strain rates is analyzed in microspall.
This paper is organized as follows.In Section 2,an improved model of damage depth of shock-melted metal in microspall is proposed.Then in Section 3,the proposed model is validated by the laser-driven shock loading experiment.In Section 4,the SPH simulations are carried out to investigate the effects of peak stress and decay length of the incident triangular wave on the damage depth.Finally,the conclusions are drawn in Section 5.
2.Proposed model
Under strong triangular wave loading,the material has already melted,and the effect of the material’s compressibility is obvious.On the other hand,the effect of the relative movement is obvious in the time from the front of the incident triangular wave reaching the free surface of the material to the completion of last spallation.Therefore,using the threshold stress criterion and rules of propagation of simple wave,a model of damage depth of shock-melted metal in microspall is proposed considering the material’s compressibility and relative movement.
When the incident triangular wave I of peak stressσmand decay length hλreflects from the free surface,the stress distribution near the free surface can be obtained on the assumption that the intensity of the reflected triangular wave R remains constant,as shown in Fig.1.The stresses of the incident triangular wave I and reflected triangular wave R inside the material at a distance d from the free surface are[(hλ−2d)/(hλ)]σmand−σm,respectively,where the parameter d represents the distance from the front of reflected triangular wave R to the free surface.Therefore,the stress inside the material at a distance d for the free surface is(2d/hλ)σm.Based on the threshold stress criterion,i.e.,dynamic spallation occurs when the tensile stress reaches spall strengthσs,after the first spallation,the thickness of spall layer d1is given by


Fig.1.Stress distribution near the free surface under triangular wave loading.The symbol I represents the incident triangular wave,the symbol R represents the reflected triangular wave,the quantitiesσm and hλdenote the peak stress and decay length of the incident triangular wave,respectively,and the quantity d represents the distance from the front of reflected triangular wave R to the free surface at the current moment.
For the remaining incident triangular wave inside the material,the peak stress isσm−σsand the decay length is hλ−2d1.If the peak stress of the incident triangular wave is high enough,the second spallation occurs,and the thickness of the spall layer remains constant.After the last spallation,the number of spall layer n and the failure depth of the material hdare

When the material is shocked above its melting pressure or melted on release from a lower shock pressure,the spall strength of melted material can be negligible compared with the peak stress,and the failure depth of the material hdcan be simplified as

However,the failure depth hdis independent of the material mass.Figure 2 gives a schematic diagram for solving the damage depth hs,which is defined as the ratio of the damage mass per unit surface area to the density at the rest condition.The main idea of solving the damage depth hsis to know the failure depth hdafter the last spallation,and to solve the damage depth hsat the moment when the front of the incident triangle wave reaches the free surface of the material,taking into account the effects of material’s compressibility and relative movement.Therefore,damage material,the substance to the right of the blue dotted line at time t2,is the substance to the right of the red dotted line at time t1.According to the propagation laws of simple wave,the expression of the damage mass msand damage depth hsinduced by the ideal triangular wave in microspall can be derived as
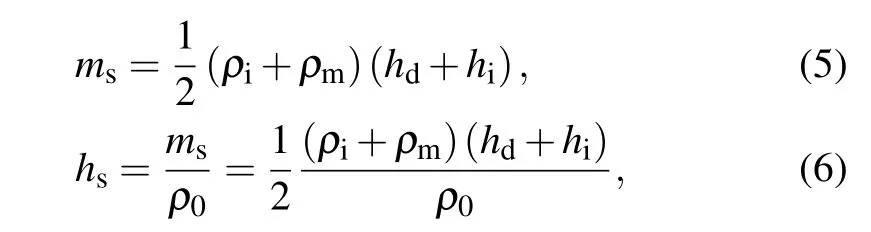
where the(1/2)(ρi+ρm)reflects the effect of material’s compressibility,the hireflects the effect of relative movement,and hi,ρmandρiare given by

According to Eqs.(4),(6)and(7),if the material parameters(ρ0,c,s),the peak velocity um(or peak stressσm=−ρ0(c0+sum)um)and decay length hλof the incident triangular wave are known,the damage depth of the melted material hscan be obtained under triangular wave loadings.The material parameters of tin are presented in Table 1.
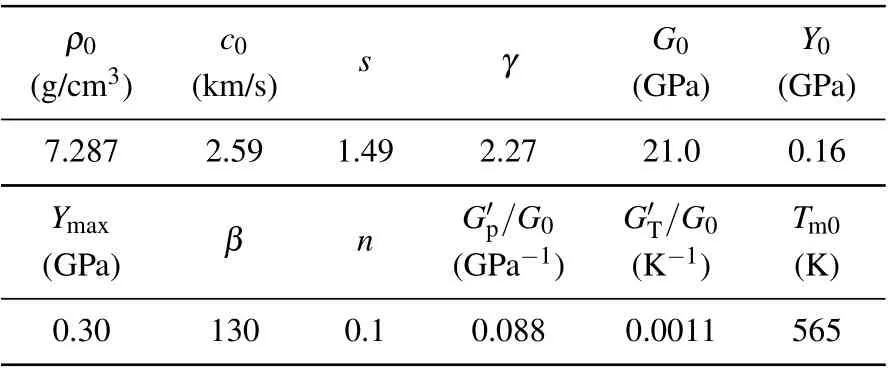
Table 1.Material parameters of tin.
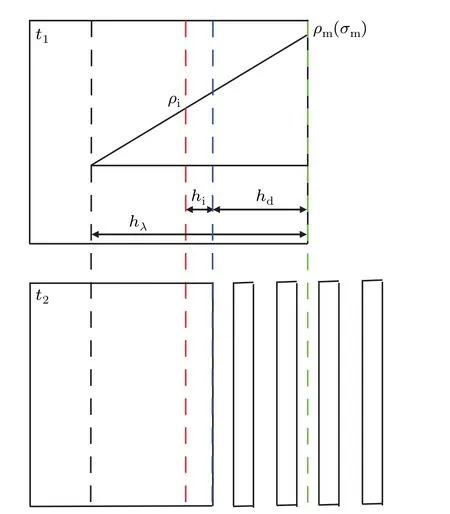
Fig.2.Schematic diagram for solving the damage depth.t1 is the moment when the incident triangular wave reaches the free surface,t2 is the moment when the last spallation ends,the blue dotted line is the position of matrix at time t2,the red dotted line is the position of blue dotted line at time t1,the green dotted line is the beginning position of incident triangular wave and the black dotted line is the end position of incident triangular wave at time t1.ρi is the density at the red dotted line at time t1,the quantitiesρm,σm and hλ denote the peak density,peak stress and decay length of the incident triangular wave at time t1,respectively,hd is the failure depth,hi is the relative movement between time t1 and t2.
3.Laser-driven experiment validation
After completing the theoretical model of the damage depth,the laser-driven experiments of microspall are performed.The damage depth obtained from the proposed model is compared with the experimental result and also compared with the model proposed by Shao et al.[23]
3.1.Experimental setup
The experiments are performed on the SGII-U laser facility.Figure 3 shows the experimental setup of microspall.[24]Two of eight driven laser beams work at 0.351µm wavelength and with 3 ns duration,and focus onto the target at 45°angle.The beams are smoothed by the continuous phase plates(CPP),and the irradiated spots are quasi circular of about 2 mm diameter on the target.
The samples are tin foil with a thickness of 500µm and a roughness of 400 nm after surface polishing.Two experiments are performed on the tin sample with the same expected energy of the driving laser.The shot 1 is the microspall experiment,and the shot 2 adds a LiF window on the tin surface under the same conditions,which is used to measure the interface velocity history with photonic Doppler velocimetry(PDV)and obtain the profile of the incident triangular wave in the sample.The actual energy measured by the energy meter in shot 1 and shot 2 are 1282 J and 1272 J,respectively.
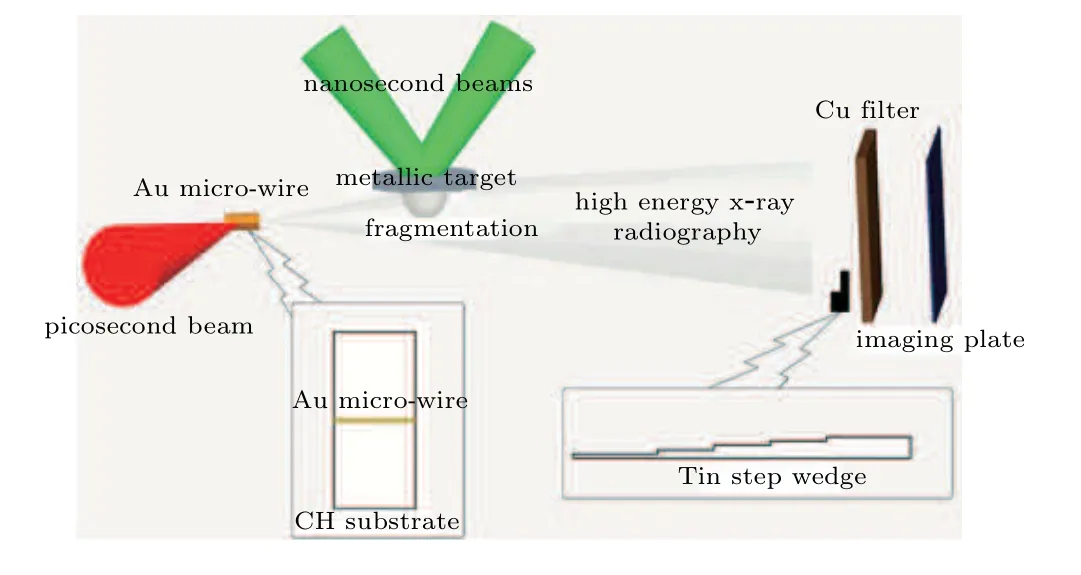
Fig.3.The experimental setup of microspall.
3.2.Experimental results and analysis

Fig.4.(a)The historical curves of the interface velocity between the tin sample and LiF in shot 2 based on PDV measurement and SPH simulation.(b)Stress profile of the incident triangular wave from SPH simulation in shot 1 and shot 2.
Figure 4(a)shows the historical curve of the interface velocity between the tin sample and LiF in shot 2 based on PDV measurement.Since the incident shock wave is a triangular wave,the interface velocity continues to decay.The selfdeveloped 2D SPH code[25,26]is used to determine the peak stress and decay length of the incident triangular wave.Therefore,the stress profile of the incident triangular wave in shot 1 and shot 2 can be determined,as shown in Fig.4(b),where the peak stress is−36 GPa and the decay length is 198µm.The historical curve of the interface velocity in SPH simulation is also shown in Fig.4(a).Based on the initial maximum and early decreasing slope of the interface velocity,which determine the peak stress and unloading rate of the incident triangular wave,it can be seen that the SPH simulation is almost consistent with the experimental result.

Table 2.The damage depth obtained from the microspall experiment and models.
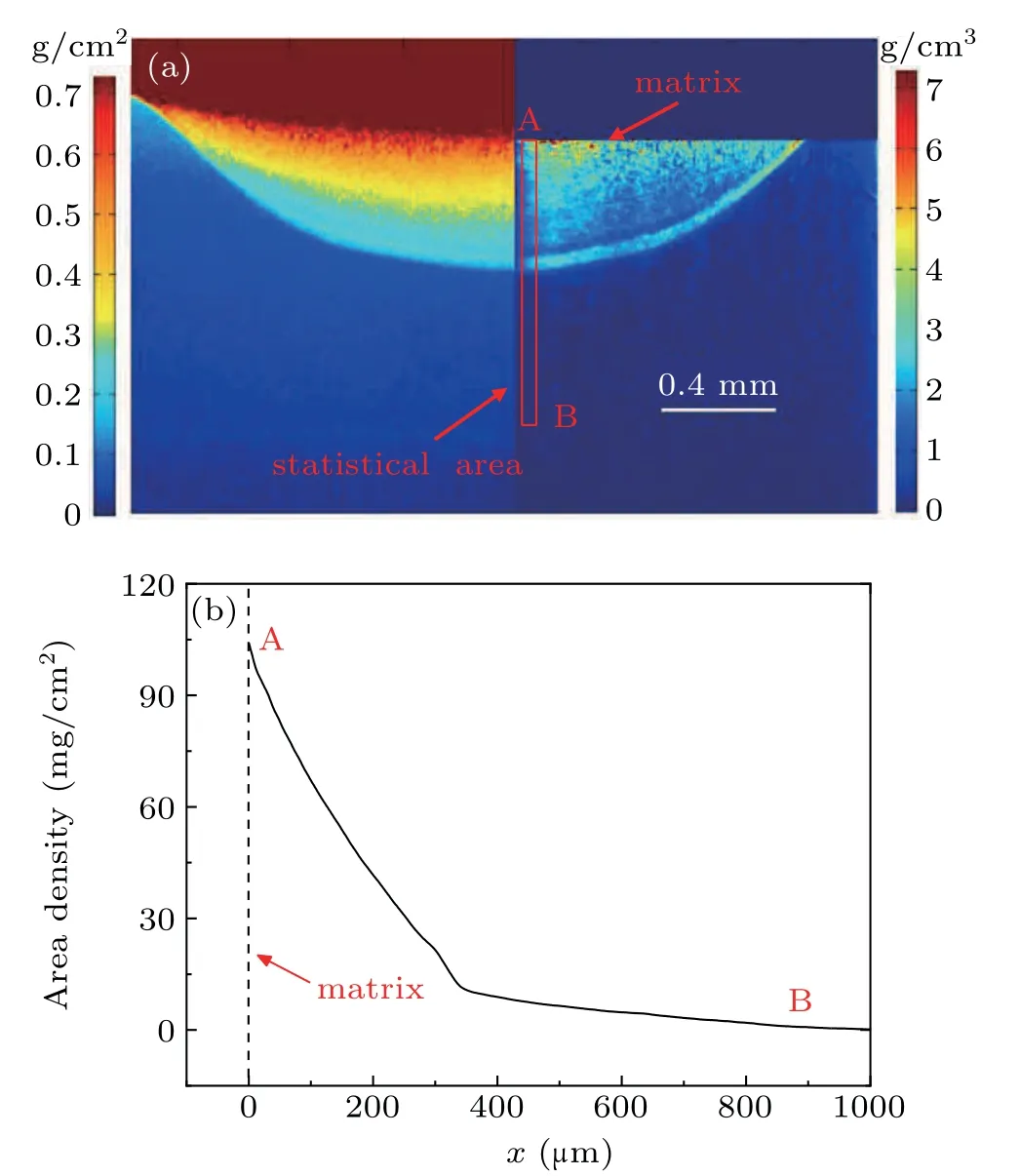
Fig.5.(a)Areal density and volume density of the x-ray radiography image in shot 1.The red box is selected to count the volume density.(b)The areal density distribution along the shock direction.The symbol A indicates the position of matrix,and the symbol B indicates the start position of the statistics.
4.The effects of peak stress and decay length on the damage depth
According to the proposed model,it can be seen that,in addition to the material parameters,the peak stress and decay length of the incident triangular wave determine the damage depth.In this section,two-groups of SPH simulations are carried out to investigate the effects of peak stress and decay length on the damage depth,respectively,and the results of the SPH simulation are compared with the proposed model.In addition,the applicability of the threshold stress criterion for melted metals at high strain rates is analyzed in microspall.
4.1.Model and method
The microspall simulations of tin are carried out using a self-developed 2D SPH code.[25,26]In the SPH method,the material is discretized into a series of particles with independent information.Due to its Lagrangian nature,SPH has the advantage of simulating free-surface flows with large deformations.[27]The pressure is modeled by the Mie–Gr¨uneisen equation of state,[28]as follows:

where theη=ρ/ρ0−1 is the compression ratio,γis the Gr¨uneisen constant,and the parameters a1,a2,and a3are given by

The Steinberg–Guinan constitutive model[29]is used,and the shear modulus strength G and yield strength Y are given as follows:

where the subscript“0”denotes the reference state(T=300 K,p=0 Pa,ε=0 s−1),εpis equivalent plastic strain,βand n are working hardening parameters,and T is the temperature.
The melting temperature is modeled using the Lindermann’s melting law[29]

where Tm0and Vm0are melting temperature and specific volume at reference state(p=0 Pa,ε=0 s−1).
The threshold stress criterion is adopted,i.e.,the tin spalls when the stress within the material is larger thanσ≥σmin=1.2 GPa.After tin melts,its spall strength is set to 0.1 GPa.[11]The material parameters of tin are presented in Table 1.

Fig.6.The profiles of the incident triangular wave in SPH simulations:(a)different decay lengths at a peak stress of−50 GPa;(b)different peak stresses at a decay length of 300µm.
In the simulation,the width of the sample is 100µm,the initial inter-particle distance is 0.25µm,and the smoothing length is 0.375µm.Different triangular waves can be obtained by changing the length of sample,the length of flyer and the velocity of flyer.In the following discussion,the time is set to 0 ns when the front of the incident triangular wave reaches the free surface of sample.Two-groups of SPH simulations are conducted to investigate the effects of peak stress and decay length on the damage depth,respectively,and the profiles of the incident triangular waves are shown in Fig.6.Figure 6(a)shows the profiles of the incident triangular waves when the peak stress is−50 GPa and the decay length is ranged from 100µm to 500µm,Figure 6(b)shows the profiles of the incident triangular waves when the decay length is 300µm and the peak stress is ranged from−30 GPa to−70 GPa.The above peak stresses indicate that the tin has melted under the given loading conditions.[30]
4.2.SPH simulation results and analysis
Figure 7 gives the result of microspall at 300 ns when the peak stress is−50 GPa and the decay length is 300µm.The black dotted line indicates the position of the matrix,so the material to the right of the black dotted line is the damage material in microspall,and the damage mass msand damage depth hs=(ms)/((1·ly)·ρ0)can be obtained,where ly=100µm is the width of the sample.
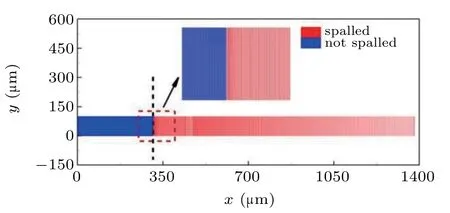
Fig.7.Microspall at 300 ns in SPH simulations when the peak stress is−50 GPa,and the decay length is 300µm.The black dotted line indicates the position of the matrix.
Figure 8 shows the results of the damage depth of the SPH simulations and the proposed model.As shown in Fig.8(a),with the increase of decay length hλ,the damage depth hsincreases linearly,and the results of the SPH simulations agree well with those of the model with a maximum error of 0.029.As shown in Fig.8(b),with the increase of peak stressσm,the damage depth hsincreases nonlinearly,the increase in damage depth gradually slows down with an increase in peak stressσm,and the results of the SPH simulations agree well with those of the model with a maximum error of 0.033.
In contrast to the free-surface velocity associated with the first spallation,the damage depth is related to the spallation inside the material.Since the threshold stress criterion is adopted in the current SPH simulations,and the damage depths obtained from the SPH simulation are in good agreement with the results of the proposed model,it can be judged that the threshold stress criterion can satisfy the requirements of microspall of melted metal.

Fig.8.The damage depth vs.(a)decay length hλand(b)peak stressσm.
5.Conclusion
In this paper,an improved model of damage depth of shock-melted metal in microspall under triangular wave loading is proposed considering the material’s compressibility and relative movement.Then,the microspall is investigated in the laser-driven shock loading experiment,and the damage depth obtained from the proposed model is compared with the experimental result.Finally,two-groups of SPH simulations are performed to investigate the effects of peak stress and decay length of the incident triangular wave on the damage depth.The details are as follows:
(I)Using the threshold stress criterion and rules of propagation of simple wave,a model of damage depth of shockmelted metal considering both the material’s compressibility and relative movement is proposed.When the physical parameters of the material,peak velocity(or peak stress)and decay length of the triangular wave are known,the damage depth of the melted metal can be obtained under triangular wave loading.The proposed model is validated by the laser-driven experiment.Compared with the previous model,the proposed model can predict the damage depth of shock-melted metal in microspall more accurately.
(II)As the decay length increases,the damage depth increases linearly.As the peak stress increases,the damage depth increases nonlinearly,and the increase in damage depth gradually slows down.The results of the SPH simulation agree well with those of the proposed model.
(III)Combining the damage depth results of the SPH simulations and the proposed model,it is found that the threshold stress criterion can reflect the macroscopic characteristics of microspall of melted metal.
- Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction∗
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing∗
- First-principles study of plasmons in doped graphene nanostructures∗
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film∗
- Signal-to-noise ratio of Raman signal measured by multichannel detectors∗
- Molecular dynamics study of coupled layer thickness and strain rate effect on tensile behaviors of Ti/Ni multilayered nanowires∗

